机器学习-线性回归

机器学习-基础知识
机器学习-线性回归
机器学习-逻辑回归
机器学习-聚类算法
机器学习-决策树算法
机器学习-集成算法
机器学习-SVM算法

1. 线性回归算法

1.1. 理论基础

​ 拟合的平面：
$$h_{\theta }(x)={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$$
​ 加上一个$x_0=1$ ，进行整合：
$$h_{\theta }(x)=\sum _{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$$
​ 样本：
$$y^{(i)}={\theta }^T{x}^{(i)}+{\epsilon }^{(i)}①$$
​ 其中${\epsilon }^{(i)}$是真实值与预测值的误差

​ 满足的条件：独立同分布，服从均值为0，方差为${\theta }^2$的高斯分布

​ 高斯分布：
$$P({\epsilon }^{(i)})=\frac{1}{\sqrt{2\pi }\sigma }\cdot exp(-\frac{({\epsilon }^{(i)}{)}^2}{2{\sigma }^2})②$$
​ 结合①+②：
$$P(y^{(i)}|x^{(i)};\theta )=\frac{1}{\sqrt{2\pi }\sigma }\cdot exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})$$
​ 似然函数：
$$L(\theta )=\prod _{i=1}^{m}P(y^{(i)}|x^{(i)};\theta )=\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\cdot exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})$$
​ 对数似然：
$$\begin{gathered} logL(\theta )=log\prod _{i=1}^{m}P(y^{(i)}|x^{(i)};\theta ) \\ =log\prod _{i=1}^m\frac{1}{\sqrt{2\pi }\sigma }\cdot exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2})似然函数取对数，让乘法操作变成加法操作 \\ =\sum _{i=1}^{m}log\frac{1}{\sqrt{2\pi }\sigma }\cdot exp(-\frac{(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2}{2{\sigma }^2}) \\ =m\cdot log\frac{1}{\sqrt{2\pi }\sigma }-\frac{1}{{\sigma }^2}\frac{1}{2}\sum _{i=1}^m(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2保证似然函数越大越好 \end{gathered}$$
​ 损失函数：
$$\begin{gathered} J(\theta )=\frac{1}{2}\sum _{i=1}^m(y^{(i)}-{\theta }^T{x}^{(i)}{)}^2 \\ =\frac{1}{2}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2转化为矩阵形式 \\ =\frac{1}{2}(X\theta -y{)}^T\cdot (X\theta -y) \end{gathered}$$
​ 对损失函数求偏导：
$$\begin{gathered} {\nabla }_{\theta }J(\theta )={\nabla }_{\theta }[\frac{1}{2}(X\theta -y{)}^T\cdot (X\theta -y)] \\ ={\nabla }_{\theta }[\frac{1}{2}({\theta }^T{X}^T-y^T)\cdot (X\theta -y)] \\ ={\nabla }_{\theta }[\frac{1}{2}({\theta }^T{X}^{T}X\theta -{\theta }^T{X}^{T}y-y^{T}X\theta +y^{T}y)] \\ =\frac{1}{2}[2X^{T}X\theta -X^{T}y-(y^{T}X{)}^T] \\ =X^{T}X\theta -X^{T}y \end{gathered}$$
​ 让偏导数为0：
$$X^{T}X\theta -X^{T}y=0=>\theta =(X^{T}X{)}^{-1}{X}^{T}y$$
​ 梯度下降：
$$\begin{gathered} 小批量梯度下降: \\ {\theta }_j^{{}^{\prime }}={\theta }_j-\alpha \sum _{k=i}^{i+9}(h_{\theta }(x^{(k)})-y^{(k)})x_j^{(k)}(每次选择10个样本) \\ 批量梯度下降: \\ {\theta }_j^{{}^{\prime }}={\theta }_j+\frac{1}{m}\sum _{i=1}^m(y^{(i)}-h_{\theta }(x^{(i)})x_j^{(i)}(每次选择所有样本) \\ 随机梯度下降: \\ {\theta }_j^{{}^{\prime }}={\theta }_j+(y^{(i)}-h_{\theta }(x^{(i)}))x_j^{(i)}(每次选择1个样本) \end{gathered}$$

1.2. 自定义的线性回归类

此处导入的包在2.模块中列出

import numpy as np
from utils.features import prepare_for_training

class LinearRegression:
    def __init__(self,data,labels,polynomial_degree=0,sinusoid_degree=0,normalize_data=True):
        """
        1.对数据进行预处理
        2.先得到所有的特征个数
        3.初始化参数矩阵
        """
        data_processed, \
        features_mean, \
        features_deviation = prepare_for_training(data, polynomial_degree, sinusoid_degree, normalize_data=True)

        self.data = data_processed
        self.labels = labels
        self.features_mean = features_mean
        self.features_deviation = features_deviation
        self.polynomial_degree = polynomial_degree
        self.sinusoid_degree = sinusoid_degree
        self.normalize_data = normalize_data

        num_features = self.data.shape[1]
        self.theta = np.zeros((num_features,1))

    def train(self,alpha,num_iterations = 500):
        """训练模块，执行梯度下降"""
        cost_history = self.gradient_descent(alpha,num_iterations)
        return self.theta,cost_history

    def gradient_descent(self,alpha,num_iterations):
        """实际迭代模块，会迭代num_num_iterations次"""
        cost_history = []
        for i in range(num_iterations):
            self.gradient_step(alpha)
            cost_history.append(self.cost_function(self.data,self.labels))
        return cost_history

    def gradient_step(self,alpha):
        """
        梯度下降参数更新计算方法,注意是矩阵运算,只执行一次
        """
        # 计算样本个数
        num_examples = self.data.shape[0]
        # 计算预测值
        prediction = self.hypothesis(self.data,self.theta)
        self.theta = self.theta - alpha*(1/num_examples)*(np.dot((prediction - self.labels).T,self.data)).T

    def cost_function(self,data,labels):
        """损失计算方法"""
        num_examples = data.shape[0]
        delta = self.hypothesis(self.data,self.theta) - labels
        cost = (1/2) * np.dot(delta.T,delta)/num_examples
        # print(cost)
        return cost[0][0]

    @staticmethod
    def hypothesis(data,theta):
        predictions = np.dot(data,theta)
        return predictions

    def get_cost(self,data,labels):
        data_processed = prepare_for_training(data,self.polynomial_degree,self.sinusoid_degree,self.normalize_data)[0]
        return self.cost_function(data_processed,labels)

    def predict(self,data):
        """用训练好的参数模型,去预测得到回归值结果"""
        data_processed = prepare_for_training(data, self.polynomial_degree, self.sinusoid_degree, self.normalize_data)[0]
        predictions = self.hypothesis(data_processed,self.theta)
        return predictions

1.3. 预处理数据包

自定义函数类中使用到的用于产生训练数据的数据集

"""Prepares the dataset for training"""

import numpy as np
from .normalize import normalize
from .generate_sinusoids import generate_sinusoids
from .generate_polynomials import generate_polynomials


def prepare_for_training(data, polynomial_degree=0, sinusoid_degree=0, normalize_data=True):

    # 计算样本总数
    num_examples = data.shape[0]

    data_processed = np.copy(data)

    # 预处理
    features_mean = 0
    features_deviation = 0
    data_normalized = data_processed
    if normalize_data:
        (
            data_normalized,
            features_mean,
            features_deviation
        ) = normalize(data_processed)

        data_processed = data_normalized

    # 特征变换sinusoidal
    if sinusoid_degree > 0:
        sinusoids = generate_sinusoids(data_normalized, sinusoid_degree)
        data_processed = np.concatenate((data_processed, sinusoids), axis=1)

    # 特征变换polynomial
    if polynomial_degree > 0:
        polynomials = generate_polynomials(data_normalized, polynomial_degree, normalize_data)
        data_processed = np.concatenate((data_processed, polynomials), axis=1)

    # 加一列1
    data_processed = np.hstack((np.ones((num_examples, 1)), data_processed))

    return data_processed, features_mean, features_deviation

1.4. 具体测试

• 导包操作

import numpy as np
import pandas as pd
import matplotlib
matplotlib.use('TKAgg')
import matplotlib.pyplot as plt
from linear_regression import LinearRegression

• 从数据集中获取数据，把数据分为数据集和测试集部分

# 选择进行训练的数据集（155行x12列的数据）,此处需要选择自己的训练集
data = pd.read_csv("data/world-happiness-report-2017.csv")
# print(data)
# 得到训练和测试数据(训练集80%,测试集20%)
train_data = data.sample(frac=0.8)
test_data = data.drop(train_data.index)

# 获取其中的两列数据进行训练
input_param_name = "Economy..GDP.per.Capita."
output_param_name = "Happiness.Score"
x_train = train_data[[input_param_name]].values
y_train = train_data[[output_param_name]].values

# 获取两列测试集
x_test = test_data[[input_param_name]].values
y_test = test_data[[output_param_name]].values

• 把训练之前的数据展示出来

# 进行画图操作
plt.scatter(x_train,y_train,label = 'Train data')
plt.scatter(x_test,y_test,label = 'test data')
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title("Happy")
plt.legend()
plt.show()

具体效果：

• 测试数据，画出相应的曲线

# 测试数据
prediction_num = 100
x_predictions = np.linspace(x_train.min(),x_train.max(),prediction_num).reshape(prediction_num,1)
y_predictions = linear_gegression.predict(x_predictions)

plt.scatter(x_train,y_train,label = 'Train data')
plt.scatter(x_test,y_test,label = 'test data')
plt.plot(x_predictions,y_predictions,"r",label = "predidtion")
plt.xlabel(input_param_name)
plt.ylabel(output_param_name)
plt.title("Happy")
plt.legend()
plt.show()

具体效果：

2. 线性回归

• 之前的算法模拟已经给出了求解方法，基于最小二乘法求解，但这并不是机器学习的思想，由此引入了梯度下降方法。

2.1. 线性回归方程的实现

1. 先进行导包操作

import numpy as np
import os
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
# 画图展示的时候字体的大小
plt.rcParams['axes.labelsize'] = 14
plt.rcParams['xtick.labelsize'] = 12
plt.rcParams['ytick.labelsize'] = 12
# 防止版本不匹配出现警告
import warnings
warnings.filterwarnings('ignore')
# 指定一个随机种子,保证每次的数据都相同
np.random.seed(42)

回归方程：

2. 随机生成X和y值

   rand函数是一个均匀分布的随机数函数，会返回0-1区间的随机数

   randn生成正态分布随机数，有正数有负数

# 产生100行1列的范围是在[0-2]的随机数
X = 2 * np.random.rand(100,1)
# 产生100行1列的服从均值为 0，标准差为 1 的正态分布的随机数
y = 3 * X + 4 + np.random.randn(100,1)

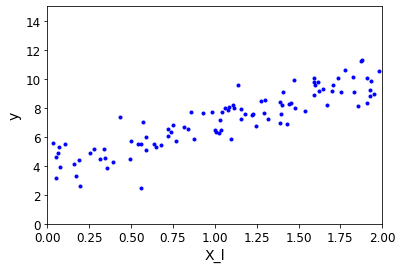
3. 把第二步生成的点出来

plt.plot(X,y,'b.')
plt.xlabel('X_l')
plt.ylabel('y')
plt.axis([0,2,0,15])
plt.show()

 效果展示：

4. 拼接数据，方便进行数据操作

# 把常数项和原数据进行拼接
X_b = np.c_[np.ones((100,1)),X]
# 具体的计算,计算曲线的斜率
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)
theta_best

5. 生成曲线的参数

# 生成两行一列的数据
X_new = np.array([[0],[2]])
# 把数据与1进行拼接
X_new_b = np.c_[np.ones((2,1)),X_new]
# 进行预测,生成曲线参数
y_predict = X_new_b.dot(theta_best)

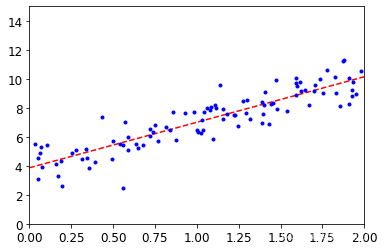
6. 根据参数画出图形

plt.plot(X_new,y_predict,'r--')
plt.plot(X,y,'b.')
plt.axis([0,2,0,15])
plt.show()

效果展示：

7. 使用工具包进行训练

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X,y)
# 获取预测的估计系数
print(lin_reg.coef_)
# 获取模型中的截距项
print(lin_reg.intercept_)

2.2. 梯度下降

• 应当合理控制步长，如果步长过大，导致数据震荡太大，无法拟合较好的曲线；如果太小，会花费很长的时间
• 标准化的作用：拿到数据后基本上都要进行一次标准化操作

2.2.1. 批量梯度下降

• 计算公式

• 批量梯度下降

# 学习率
eta = 0.1
# 迭代次数
n_iterations = 1000
# 样本总量
m = 100
# 设置一个随机的theta值
theta = np.random.randn(2,1)
# 进行迭代
for iteration in range(n_iterations):
  	# 批量梯度下降的具体计算公式
    gradients = 2/m * X_b.T.dot(X_b.dot(theta)-y)
    theta = theta - eta * gradients

• 画图操作，注意与上面是独立的

# 画图操作
# 选择theta=0.1的学习率放入theta_path_bgd,后面用于数据的比较
theta_path_bgd = []
def plot_gradient_descent(theta,eta,theta_path = None):
    m = len(X_b)
    plt.plot(X,y,'b.')
    n_iterations = 1000
    for iteration in range(n_iterations):
        y_predict = X_new_b.dot(theta)
        plt.plot(X_new,y_predict,'r-')
        gradients = 2/m * X_b.T.dot(X_b.dot(theta)-y)
        theta = theta - eta * gradients
        if theta_path is not None:
            theta_path_bgd.append(theta)
    plt.xlabel('X_1')
    plt.axis([0,2,0,15])
    plt.title('eta = {}'.format(eta))
    
    
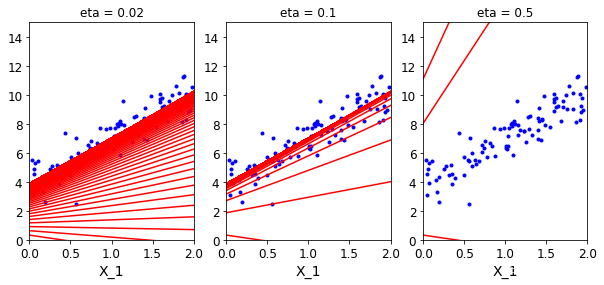
# 保证theta相同的条件下，改变eta的值，来判断预测函数
theta = np.random.randn(2,1)
plt.figure(figsize=(10,4))
plt.subplot(131)
plot_gradient_descent(theta,eta = 0.02)
plt.subplot(132)
plot_gradient_descent(theta,eta = 0.1,theta_path=True)
plt.subplot(133)
plot_gradient_descent(theta,eta = 0.5)
plt.show()

效果展示：

2.2.2. 随机梯度下降

• 迭代的次数会越来越多

# 随机梯度下降，每次迭代1个数据

# 保存随机的theta值 
theta_path_sgd = []
# 回传一个两行一列的数组
theta = np.random.randn(2,1)
m = len(X_b)
n_epochs = 50

# 指定衰减策略
t0 = 5
t1 = 50
# 随着迭代的进行,值会越来越小
def learning_schedule(t):
    return t0/(t1+t)
    
for epoch in range(n_epochs):
    for i in range(m):
        # 为了方便显示，只迭代前几次
        if epoch == 10 and i < 20:
            y_predict = X_new_b.dot(theta)
            plt.plot(X_new,y_predict,'r-')
        # 选择随机的一个样本
        random_index = np.random.randint(m)
        xi = X_b[random_index:random_index+1]
        yi = y[random_index:random_index+1]
        # 计算梯度
        gradients = 2 * xi.T.dot(xi.dot(theta)-yi)
        # 根据衰减策略进行迭代
        eta = learning_schedule(epoch * m + i)
        theta = theta - eta * gradients
        theta_path_sgd.append(theta)  

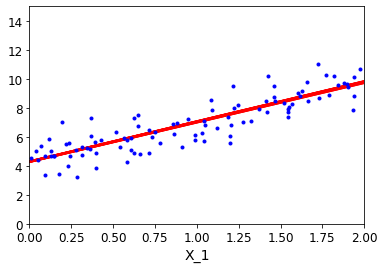
 # 展示
 plt.plot(X,y,'b.')
 plt.xlabel('X_1')
 plt.axis([0,2,0,15])
 plt.show()

效果展示：

2.2.3. MiniBatch梯度下降

• 迭代的次数一般为2的整数倍

 theta_path_mgd = []
 n_epochs = 50
 # 每次选择16个数据进行迭代
 minibatch = 16
 theta = np.random.randn(2,1)
 
 t = 0
 for epoch in range(n_epochs):
     shuffled_indices = np.random.permutation(m)
     X_b_shuffled = X_b[shuffled_indices]
     y_shuffled = y[shuffled_indices]
     for i in range(0,m,minibatch):
          # 为了方便显示，只迭代前几次
         if epoch == 40 :
             y_predict = X_new_b.dot(theta)
             plt.plot(X_new,y_predict,'r-')
         t += 1
         xi = X_b_shuffled[i:i + minibatch]
         yi = y_shuffled[i:i + minibatch]
         gradients = 2/minibatch * xi.T.dot(xi.dot(theta)-yi)
         eta = learning_schedule(t)
         theta = theta - eta * gradients
         theta_path_mgd.append(theta)
 
 plt.plot(X,y,'b.')
 plt.xlabel('X_1')
 plt.axis([0,2,0,15])
 plt.show()

效果展示：

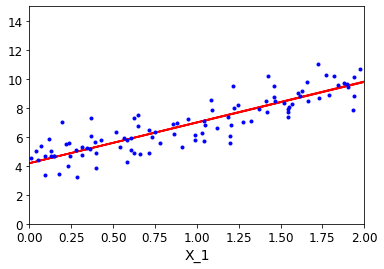
2.2.4. 三种策略的对比

• 对比实验

theta_path_bgd = np.array(theta_path_bgd)
theta_path_sgd = np.array(theta_path_sgd)
theta_path_mgd = np.array(theta_path_mgd)


plt.figure(figsize=(8,4))
# 批量梯度下降
plt.plot(theta_path_bgd[:,0],theta_path_bgd[:,1],'b-o',linewidth=1,label='BGD')
# 随机梯度下降
plt.plot(theta_path_sgd[:,0],theta_path_sgd[:,1],'r-s',linewidth=1,label='SGD')
# 小批量梯度下降
plt.plot(theta_path_mgd[:,0],theta_path_mgd[:,1],'g-+',linewidth=1,label='MGD')
plt.legend(loc='upper left')

效果展示：

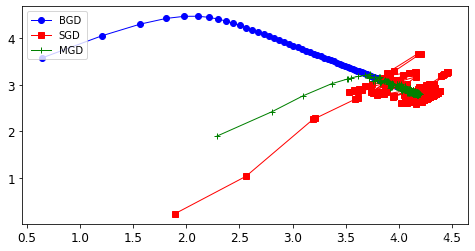
3. 非线性回归

3.1. 算法模拟

• 模拟数据

m = 100
X = 6 * np.random.rand(m,1) - 3
y = 0.5 * X ** 2 + X + np.random.randn(m,1)

• 展示

plt.plot(X,y,'b.')
plt.xlabel('X')
plt.ylabel('y')
plt.axis([-3,3,-5,8])
plt.show()

效果展示：

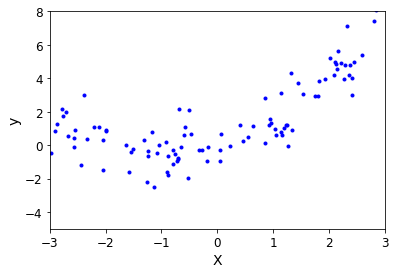
• 多项式运算

from sklearn.preprocessing import PolynomialFeatures
# 生成二次函数
poly_features = PolynomialFeatures(degree = 2,include_bias = False)
# 拟合数据，然后对其进行转换,fit函数用于计算各项值，transform用于转化数据，把数据进行回传
# 回传原数据和原数据的平方项
X_poly = poly_features.fit_transform(X)

获取平方项，一次项和常数项

from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X_poly,y)
print(lin_reg.coef_)
print(lin_reg.intercept_)

画图展示

# 画图操作
X_new = np.linspace(-3,3,100).reshape(100,1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)
plt.plot(X,y,'b.')
plt.plot(X_new,y_new,'g-',label = 'prediction')
plt.axis([-3,3,-5,10])
plt.legend()
plt.show()

效果展示：

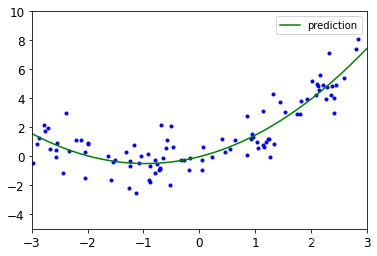
• 特征变换复杂度

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
plt.figure(figsize=(12,8))
# 相应位置相互对应
for style,width,degree in (('g-',1,100),('b--',2,2),('r-+',1,1)):
    # 生成管道所需要的变量
    poly_features = PolynomialFeatures(degree = degree,include_bias = False)
    std = StandardScaler()
    lin_reg = LinearRegression()
    # 管道操作
    polynomial_reg = Pipeline([('poly_features',poly_features),
            ('StandardScaler',std),
            ('lin_reg',lin_reg)])
    # 训练
    polynomial_reg.fit(X,y)
    # 预测
    y_new_2 = polynomial_reg.predict(X_new)
    # 展示
    plt.plot(X_new,y_new_2,style,label = 'degree'+str(degree),linewidth = width)
plt.plot(X,y,'b.')
plt.axis([-3,3,-5,10])

plt.legend()
plt.show()

效果展示：

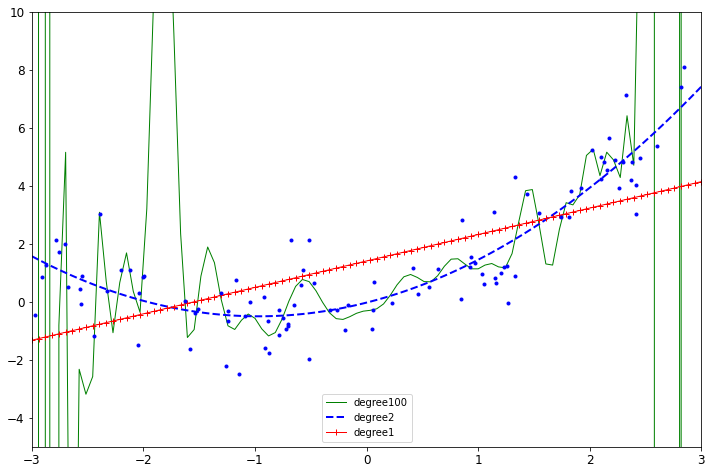
特征变换的越复杂，得到的结果过拟合风险越高，不建议做的特别复杂。

• 样本数量对结果的影响

 # 导入均方误差函数
 from sklearn.metrics import mean_squared_error
 # 将数组或矩阵拆分为随机训练和测试子集
 from sklearn.model_selection import train_test_split
 
 def plot_learning_curves(model,X,y):
     # 将数据进行拆分，测试集的比例是0.2，指定随机因子，保证每次传的值相同
     X_train,X_val,y_train,y_val = train_test_split(X,y,test_size = 0.2, random_state = 0)
     
     train_errors,val_errors = [],[]
     for m in range(1,len(X_train)):
         # 选择m个数据进行训练
         model.fit(X_train[:m],y_train[:m])
         # 训练集的结果
         y_train_predict = model.predict(X_train[:m])
         # 测试集的结果
         y_val_predict = model.predict(X_val)
         
         train_errors.append(mean_squared_error(y_train[:m],y_train_predict[:m]))
         val_errors.append(mean_squared_error(y_val,y_val_predict))
     plt.plot(np.sqrt(train_errors),'r-+',linewidth = 1,label = 'train_error')
     plt.plot(np.sqrt(val_errors),'b-',linewidth = 2,label = 'val_error')
     plt.xlabel('Trainsing set size')
     plt.ylabel('RMSE')
     plt.legend()

展示

lin_reg = LinearRegression()
plot_learning_curves(lin_reg,X,y)
plt.axis([0,80,0,3.3])
plt.show()

效果展示：

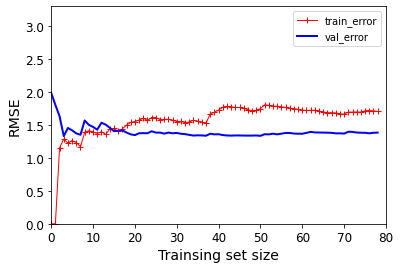
• 过拟合风险(越复杂越过拟合)

 # 生成流水线
 polynomial_reg = Pipeline([('poly_features',PolynomialFeatures(degree = 25,include_bias = False)),('lin_reg',LinearRegression())])
 plot_learning_curves(polynomial_reg,X,y)
 
 plt.axis([0,80,0,5])
 plt.show()

效果展示：

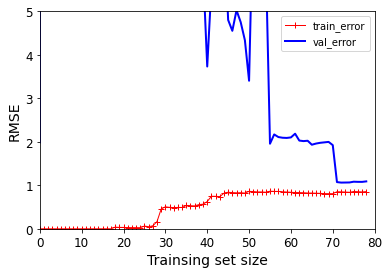
3.2. 正则化

​ 对权重参数进行惩罚，让权重参数尽可能平滑一些，有两种不同的方法来进行正则化惩罚:
$$J(\theta )=MSE(\theta )+\alpha \frac{1}{2}\sum _{i=1}^n{\theta }_i^2$$

# 导入岭回归的包
from sklearn.linear_model import Ridge
# 指定随机种子
np.random.seed(42)
# 样本的数量
m = 20
# X的数据在0-3之间
X = 3 * np.random.rand(m,1)
# y的值
y = 0.5 * X + np.random.randn(m,1)/1.5 +  1
# 测试数据：指定0-3的100个数据，并且把数据转换成数组的形式
X_new = np.linspace(0,3,100).reshape(100,1)

def plot_model(model_calss,polynomial,alphas,**model_kargs):
   # zip函数让alphas与括号里面的线条相对应，赋给循环变量alpha和style
   for alpha,style in zip(alphas,('b-','g--','r:')):
       # 线性回归模型
       model = model_calss(alpha,**model_kargs)
       # 二项式回归模型
       if polynomial:
           model = Pipeline([('poly_features',PolynomialFeatures(degree =10,include_bias = False)),('StandardScaler',StandardScaler()),
   ('lin_reg',model)])
       # 训练
       model.fit(X,y)
       # 预测
       y_new_regul = model.predict(X_new)
       # 画图展示
       lw = 2 if alpha > 0 else 1
       plt.plot(X_new,y_new_regul,style,linewidth = lw,label = 'alpha = {}'.format(alpha))
   plt.plot(X,y,'b.',linewidth =3)
   plt.legend()

plt.figure(figsize=(14,6))
plt.subplot(121)
plot_model(Ridge,polynomial=False,alphas = (0,10,100))
plt.subplot(122)
plot_model(Ridge,polynomial=True,alphas = (0,10**-5,1))
plt.show()

效果展示：

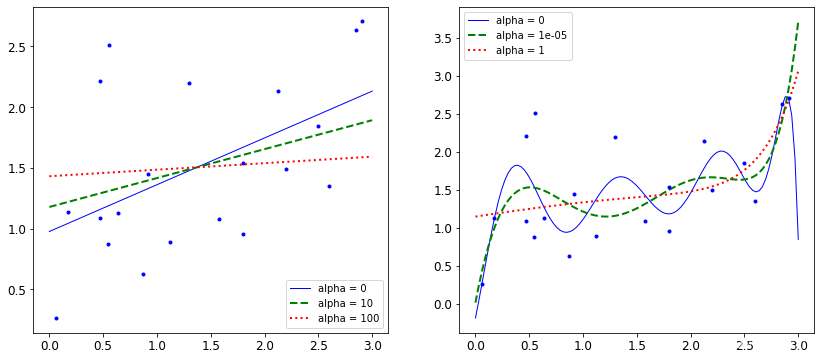
惩罚力度越大，alpha值越大的时候，得到的决策方程越平稳。
$$J(\theta )=MSE(\theta )+\alpha \sum _{i=1}^n|{\theta }_i|$$

from sklearn.linear_model import Lasso

plt.figure(figsize=(14,6))
plt.subplot(121)
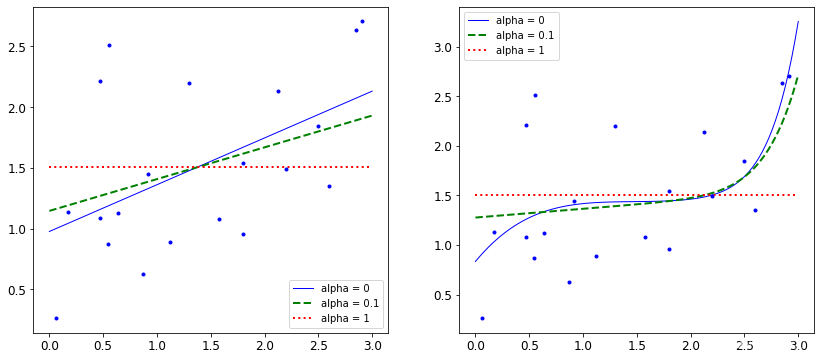
plot_model(Lasso,polynomial=False,alphas = (0,0.1,1))
plt.subplot(122)
plot_model(Lasso,polynomial=True,alphas = (0,10**-1,1))
plt.show()

效果展示：