数理统计与描述性分析

一、 样本

1.1 定义

定义：在数理统计中，称研究对象的全体为总体，通常用一个随机变量表示总体。组成总体的每个基本单元叫个体。从总体 $X$ 中随机抽取一部分个体 $X_1,X_2,...,X_n$ ,称 $X_1,X_2,...,X_n$ 为取自 $X$ 的容量为 $n$ 的样本。

样本具有两重性，即当在一次具体地抽样后它是一组确定的数值。但在一般叙述中样本也是一组随机变量，因为抽样是随机的。一般地，用 $X_1,X_2,...，X_n$ , 表示随机样本，它们取到的值记为 $x_1,x_2,...，x_n$ 称为样本观测值。

样本分布取决于总体的性质和样本的性质。

1.2 样本均值和方差

样本均值
设 $X_1,X_2,...,X_n$ 是总体 $X$ 的一个简单随机样本，称 $$\overline{X}=\frac{1}{n}\sum _{i=1}^n{X}_i$$ 为样本均值。通常用样本均值来估计总体分布的均值和对有关总体分布均值的假设作检验。

样本方差
设 $X_1,X_2,...,X_n$ 是总体 $X$ 的一个简单随机样本，$\overline{X}$ 为样本均值，称 $$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\overline{X}{)}^2$$ 为样本方差。通常用样本方差来估计总体分布的方差和对有关总体分布均值或方差的假设作检验。

1.3 有关证明

设 $x_1,x_2,...，x_n$，为总体的一个样本，且其样本均值为$\overline{X}$，样本方差为$S^2$，总体方差为$\sigma ²$，总体期望为$\mu$。

证明1：样本期望等于总体期望。
对于简单随机抽样的样本：$x_1,x_2,...，x_n$与总体X是同分布的，所以各样本的期望均为总体期望。
$$E(\overline{X})=E(\frac{1}{n}\sum _{i=1}^n{x}_i)=\frac{1}{n}\sum _{i=1}^{n}E(x_i)=\frac{1}{n}\ast n\ast E(X)=\mu$$

证明2：样本均值的方差等于$\frac{{\sigma }^2}{n}$。
$$D(\overline{X})=D(\frac{1}{n}\sum _{i=1}^n{x}_i)=\frac{1}{n^2}\sum _{i=1}^{n}D(x_i)=\frac{\sigma ²}{n}$$

证明3：样本方差的期望等于总体的方差$。


             
             
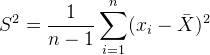
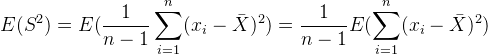
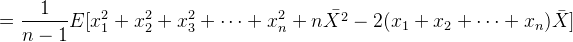
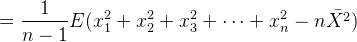
方差公式：


因此：


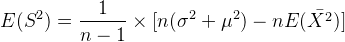
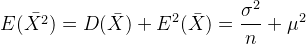
由此得到：

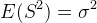
二、 描述性统计

1.1 中位数、众数、分位数

Python实现：

import numpy as np 
import pandas as pd
a=[np.random.randint(1,10) for i in range(0,20)]
a_mean = np.mean(a)  #均值
a_med = np.median(a)  #中位数
print("a的平均数:",a_mean)
print("a的中位数:",a_med)
ser = pd.Series(a)
a_m2 = ser.mode()
print("a的众数:",a_m2)
a_quan=ser.quantile(0.75)   #四分之三分位数
print(a_quan)

1.2 方差、标准差、变异系数

变异系数：
$$CV=100\ast \frac{s}{\overline{X}}$$$$s:标准差$$$$\overline{X}:平均值$$
优点：可以消除测量尺度和量纲的影响。
缺点：当均值接近于0时，微小的变化也会对变异系数造成巨大的影响；另外，它无法发展出类似于均值的置信区间的工具。

Python实现：

import numpy as np 
a=[np.random.randint(1,10) for i in range(0,20)]
a_var = np.var(a)  #方差
a_std = np.std(a) #标准差
a_mean = np.mean(a)  #均值
a_cv =  a_std /a_mean #变异系数
print("a的方差:",a_var)
print("a的标准差:",a_std)
print("a的变异系数:",a_cv)

1.3 偏度、峰度

偏度（peakedness;kurtosis)也称为偏态，是统计数据分布偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。直观看来就是密度函数曲线尾部的相对长度。偏度刻画的是分布函数（数据）的对称性。关于均值对称的数据其偏度系数为0，右侧更分散的数据偏度系数为正，左侧更分散的数据偏度系数为负。

正态分布的偏度为0，峰度为3。

左偏:
若以bs表示偏度。bs<0称分布具有负偏离，也称左偏态；
此时数据位于均值左边的比位于右边的少，直观表现为左边的尾部相对于与右边的尾部要长；
因为有少数变量值很小，使曲线左侧尾部拖得很长；

右偏：

bs>0称分布具有正偏离，也称右偏态；
此时数据位于均值右边的比位于左边的少，直观表现为右边的尾部相对于与左边的尾部要长；
因为有少数变量值很大，使曲线右侧尾部拖得很长；

峰度（peakedness;kurtosis）说明的是分布曲线在平均值处峰值高低的特征数。直观看来，峰度反映了峰部的尖度。样本的峰度是和正态分布相比较而言统计量，如果峰度大于三，峰的形状比较尖，比正态分布峰要陡峭。反之亦然。峰度刻画的是分布函数的集中和分散程度。
注：由于计算方法的不同，pandas中正态分布的峰度为0。

Python实现：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
data = list(np.random.randn(10000))
#生成标准正态分布的随机数（10000个）
plt.hist(data,1000,facecolor='g',alpha=0.5)
'''
plt.hist(arr, bins=10, facecolor, edgecolor,alpha，histtype='bar')
bins：直方图的柱数，可选项，默认为10
alpha: 透明度
'''
plt.show()
s = pd.Series(data) #将数组转化为序列
print('偏度系数',s.skew())
print('峰度系数',s.kurt())