【心脏仿真】基于龙格库塔法实现心室心肌细胞动作电位仿真附Matlab代码

本文链接：https://blog.csdn.net/Matlab_dashi/article/details/136955709

✅作者简介：热爱科研的Matlab仿真开发者，擅长数据处理、建模仿真、程序设计、完整代码获取、论文复现及科研仿真。

🍎个人主页：Matlab科研工作室

🍊个人信条：格物致知，求助可私信。

🔥 内容介绍

心脏电生理学仿真在心脏病学研究中发挥着至关重要的作用。本文介绍了一种基于龙格库塔法的数值方法，用于仿真心室心肌细胞的动作电位。该方法准确且高效，可以用于研究心脏电生理学和心脏病的机制。

引言

心脏电生理学是研究心脏电活动及其与心脏功能关系的学科。动作电位是心脏电活动的基本单位，它描述了心肌细胞膜电位的变化。动作电位的仿真对于理解心脏电生理学和心脏病的机制至关重要。

龙格库塔法

龙格库塔法是一种显式数值方法，用于求解常微分方程。它是一种单步方法，这意味着它使用当前时间步长的数据来计算下一个时间步长的数据。龙格库塔法有不同的阶数，其中四阶龙格库塔法（RK4）是最常用的。

RK4 方法的公式如下：

y_{n+1} = y_n + h * (k_1 + 2 * k_2 + 2 * k_3 + k_4) / 6

其中：

y_n 是当前时间步长 t_n 处的值
y_{n+1} 是下一个时间步长 t_{n+1} 处的值
h 是时间步长
k_1、k_2、k_3 和 k_4 是中间斜率，计算如下：

k_1 = f(t_n, y_n) k_2 = f(t_n + h/2, y_n + h/2 * k_1) k_3 = f(t_n + h/2, y_n + h/2 * k_2) k_4 = f(t_n + h, y_n + h * k_3)

心室心肌细胞模型

心室心肌细胞的动作电位可以由以下常微分方程系统描述：

C_m * dV/dt = -I_ion + I_stim

其中：

C_m 是细胞膜电容
V 是膜电位
I_ion 是离子电流
I_stim 是刺激电流

离子电流可以进一步分解为以下分量：

I_ion = I_Na + I_CaL + I_Ks + I_Kr + I_to + I_K1

其中：

I_Na 是钠电流
I_CaL 是钙电流
I_Ks 是慢延迟整流钾电流
I_Kr 是快速延迟整流钾电流
I_to 是瞬时外向整流钾电流
I_K1 是内向整流钾电流

仿真方法

我们使用 RK4 方法求解上述常微分方程系统。仿真步骤如下：

初始化细胞膜电位和离子电流。
计算中间斜率 k_1、k_2、k_3 和 k_4。
更新细胞膜电位和离子电流。
重复步骤 2 和 3 直到达到仿真时间。

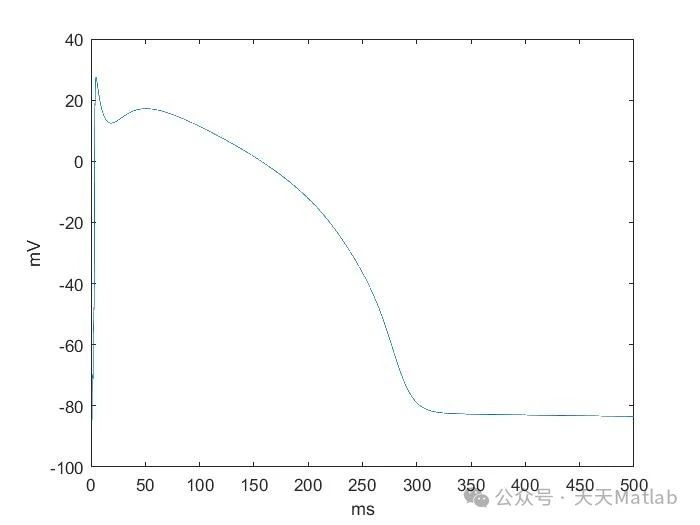
仿真结果

图 1 显示了使用 RK4 方法仿真的典型心室心肌细胞动作电位。动作电位包括以下阶段：

**去极化：**动作电位由快速去极化开始，主要是由钠电流引起的。
**高原：**去极化后，膜电位保持在高原阶段，主要是由钙电流引起的。
**复极化：**高原后，膜电位复极化，主要是由钾电流引起的。

![图 1：心室心肌细胞动作电位仿真](图 1.png)

讨论

基于 RK4 法的心室心肌细胞动作电位仿真准确且高效。该方法可以用于研究心脏电生理学和心脏病的机制。例如，该方法可以用于仿真心律失常、心脏肥大和心肌梗塞等心脏疾病。

结论

本文介绍了一种基于 RK4 法的心室心肌细胞动作电位仿真方法。该方法准确且高效，可以用于研究心脏电生理学和心脏病的机制。

📣 部分代码

%*************************************************************************%%   Beeler-Reuter Ventricular Myocyte AP Model                            %                                               %%   Description: This function returns the values of the time derivatives %%   of state variables for use in numerical integration of the solution.  %%   Most fixed model parameters are contained within this function.       %%*************************************************************************%function pdot = BR_deriv(t,p,i_stim)%-----------------------------------------------%%----------------Extract St. Vars---------------%%-----------------------------------------------%Vm   = p(1);     %[mV] - Transmembrane VoltageCa_i = p(2);     %[mol] - Intracellular Calcium%These six are unitless channel gating parametersx1 = p(3);     m  = p(4);h  = p(5);j  = p(6);d  = p(7);f  = p(8);%These four are ionic currents - not state var's; for output purposes onlyi_K1old = p(9);i_Naold = p(10);i_Caold = p(11);i_x1old = p(12);%-----------------------------------------------%%----------------Model Parameters---------------%%-----------------------------------------------%E_Na  = 50.0;        %[mV]        - Nernst potential from Nag_Na  = 4.0;         %[mmho/cm^2] - Membrane conductance parameterg_NaC = 0.003;       %[mmho/cm^2] - Membrane conductance parameterg_s   = 0.09;        %[mmho/cm^2] - Membrane conductance parameterC_m   = 1.0;         %[uF/cm^2]   - Membrane capacitance%Rate constant parameters for determining alpha and betaC(:,:,1) = [5e-4   8.3e-2  50  0   0   5.7e-2  1; ...            0      0       47  -1  47  -0.1   -1; ...            0.126  -0.25   77  0   0   0       0; ...            5.5e-2 -0.25   78  0   0   -0.2    1; ...            9.5e-2 -0.01   -5  0   0   -0.072  1; ...            1.2e-2 -8.0e-3 28  0   0   0.15    1];      C(:,:,2) = [1.3e-3 -6.0e-2 20  0   0   -4.0e-2 1; ...            40     -5.6e-2 72  0   0   0       0; ...            1.7    0      22.5 0   0   -8.2e-2 1; ...            0.3    0       32  0   0   -0.1    1; ...            7.0e-2 -1.7e-2 44  0   0   5.0e-2  1; ...            6.5e-3 -2.0e-2 30  0   0   -0.2    1];%-----------------------------------------------%%------------Preliminary Calculations-----------%%-----------------------------------------------%%Calculate alpha and beta valuesa_b = (C(:,1,:) .* exp(C(:,2,:) .* (Vm + C(:,3,:))) + C(:,4,:) .* (Vm + C(:,5,:)))...            ./(exp(C(:,6,:) .* (Vm + C(:,3,:))) + C(:,7,:));%Calculate y_inf and tauy_inf = a_b(:,:,1)./(a_b(:,:,1) + a_b(:,:,2));tau   = (a_b(:,:,1) + a_b(:,:,2)).^-1;E_Ca  = -82.3 - 13.0287 * log(Ca_i);%-----------------------------------------------%%----------Ionic Current Calculations-----------%%-----------------------------------------------%i_K1 = 0.35 * (4 * (exp(0.04 * (Vm + 85)) - 1) / (exp(0.08 * (Vm + 53))...     + exp(0.04 * (Vm + 53))) + 0.2 * ((Vm + 23) / (1 - exp(-0.04 * (Vm + 23)))));i_x1 = (x1) * 0.8 * (exp(0.04 * (Vm + 77)) - 1)/exp(0.04 * (Vm + 35));i_Na = (g_Na * m^3 * h * j + g_NaC) * (Vm - E_Na);i_Ca = g_s * d * f * (Vm - E_Ca);%-----------------------------------------------%%------------Derivative Calculations------------%%-----------------------------------------------%pdot(1,1)   = -(1/C_m) * (i_K1 + i_x1 + i_Na + i_Ca - i_stim);  %dVm/dtpdot(2,1)   = -1e-7 * i_Ca + 0.07 * (1e-7 - Ca_i);              %d[Ca]/dtpdot(3:8,1) = (y_inf - p(3:8)) ./ tau;pdot(9,1)   = i_K1 - i_K1old;pdot(10,1)  = i_Na - i_Naold;pdot(11,1)  = i_Ca - i_Caold;pdot(12,1)  = i_x1 - i_x1old;