Comsol仿真二维光子晶体的能带和全场仿真

文章来源：Ultracompact Photonic Circuits without Cladding Layers。

添加图片注释，不超过 140 字（可选）

一般光波导的原理是利用全反射，如Fig. 1a。这种光波导需要芯层的折射率大于包层折射率，当入射角大于临界角时，光会发生全反射，从而只能沿着波导传播。基本物理可以由等频线来理解，即横向波矢不匹配引起的。第二种光波导是利用光子带隙（PBGs）来实现，在对应禁带范围的光只能在芯层传播。对应的等频线是包层没有支持的传播模式，光只能沿着芯层传播。利用拓扑边界态也可以实现光的传输，最近十几年是凝聚态物理中的大热。相比于通常的全反射，后两者不依赖于入射角度，只与支持的模式有关，因此可以构造弯曲波导。赖老师课题组提出了一种新的波导结构，这种波导没有严格区分芯层和包层，即芯层和包层都可以传输光。文章用了“ultracompact”一词，在以后光子集成方面具有潜在的应用价值。

为什么这种波导的芯层和包层都可以导波而相互之间不会发生串扰呢？这就要从等频线说起。如Fig. 1c，两种介质的等频线是分离的，即完全不满足阻抗匹配。这样的结果是在A中的光只能在A中传播，不会跑到B中；同理在B中也是。这与我写的上一个帖子的情形恰好相反。我们很容易看出，这种波导不依赖入射角（只与支持的传播模式有关），因此很容易构造弯曲波导以及光子回路。

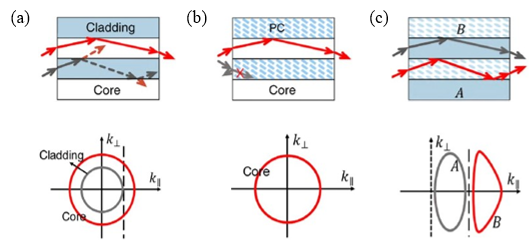
Fig. 1 三种波导及相应的等频线

为什么这种波导的芯层和包层都可以导波而相互之间不会发生串扰呢？这就要从等频线说起。如Fig. 1c，两种介质的等频线是分离的，即完全不满足阻抗匹配。这样的结果是在A中的光只能在A中传播，不会跑到B中；同理在B中也是。这与我写的上一个帖子的情形恰好相反。我们很容易看出，这种波导不依赖入射角（只与支持的传播模式有关），因此很容易构造弯曲波导以及光子回路。

文章以二维PC为例，研究了两种原胞结构，具有C4对称性和C2对称性的原胞。对应的能带图如下。在研究的频率点上，C2对称性的PC对应的等频图与Air的等频图没有相交点（原文Fig. 2），正好满足文中横向波矢完全不匹配的条件。

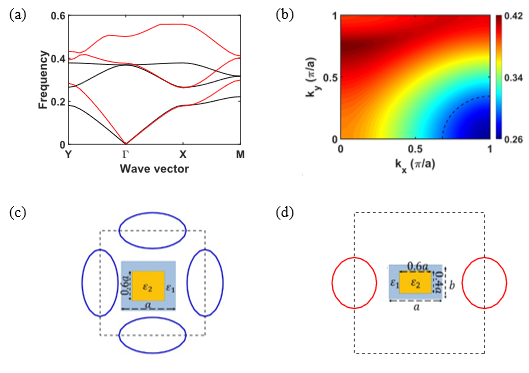
Fig. 2 C4和C2对称性原胞的能带及等频线

为了构造波导结构，需要计算PC的传输效率，文章研究了不同层数对透射率的影响，并从Air和PC阻抗差的角度解释了为什么该结构具有高的透射率。阻抗匹配的计算参考我上一个帖子

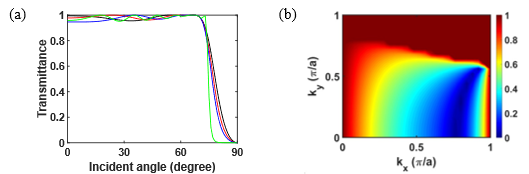
Fig. 3 透射率和阻抗差

由于要构成波导，需要计算波导的色散关系，找出相应的模式，在全场仿真中激发相应的模式，如原文Fig. 3c-3e。

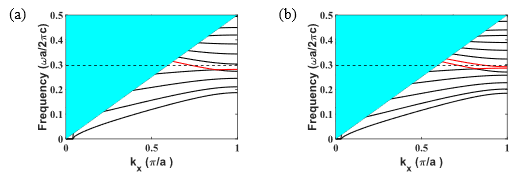
Fig. 4 两种波导的色散关系

需要说明的是，我仿真出来的能带没有交叉。第二是在0Hz附近，可能是伪模的出现（基准频率没选好，也是水平有限），与原文有一定的差别。其他结果与原文一致。

接下里文中展示了任意波导宽度下的全场仿真。我在这里给出了原文的Fig. 4cfi的场图，并给出了出射端的强度分布。很容易看出：（1）不同通道之间没有串扰；（2）不同通道之间可以做相互的包层。

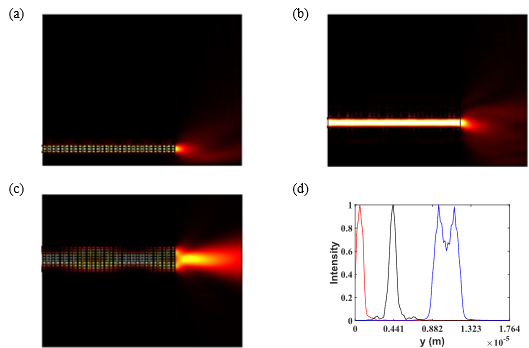
添加图片注释，不超过 140 字（可选）

Fig. 5d需要说明两点；场是归一化的，因此放在了一张图上；蓝线出现两个峰是我贴着界面提取的场，Fig. 5c也可以看出场有断点。原文是在距右端口有一定距离提取出来的场强度，因此只有一个峰。

前面我们就提到过，因为这种波导入射不依赖于入射角，因此很容易构造完全波导，进一步构造光子回路。如原文Fig. 5c-f。

Fig. 6 弯曲波导和光子回路

文章内容就讲到这里。非常膜拜赖耘老师，总是在简单的体系中构造新奇的玩意。这里面的物理，讲出来都很明白。但是，在没有看到这篇文章之前，怎么会想到利用两个不相交的等频线构造古里古怪的波导？简而言之，这里面只包含了一个物理，就是横向波矢不匹配，跟全反射的物理是一致的。真的是来源于全反射，而高于全反射。这就是大佬的玩法。