一、数据预处理
1、缺失值
对本数据集的缺失值统一用0.04填充(excel替换)


对表单1缺失的颜色用众数浅蓝填充(excel替换)


2、删除不符合要求的成分数据

将表单2中成分数据之和位于85%~105%外的样本进行剔除
故剔除文物采样点“15”和“17”
3、数据中心对数比变换(CLR)
import pandas as pd
import numpy as np
# 读取Excel文件
file_path = "E:/C题/2022/数据预处理/CLR处理表单2,表单3(1).xlsx"
xls = pd.ExcelFile(file_path)
# 读取表单2和表单3的数据
df_sheet2 = pd.read_excel(xls, '表单2_CLR')
df_sheet3 = pd.read_excel(xls, '表单3_CLR')
# 将所有列转换为数值类型,非数值将被替换为NaN
df_sheet2_numeric = df_sheet2.apply(pd.to_numeric, errors='coerce')
df_sheet3_numeric = df_sheet3.apply(pd.to_numeric, errors='coerce')
# 删除全为NaN值的列
df_sheet2_numeric.dropna(axis=1, how='all', inplace=True)
df_sheet3_numeric.dropna(axis=1, how='all', inplace=True)
# 定义执行CLR变换的函数
def clr_transformation(df):
# 将零值替换为一个很小的数,以避免除以零
df = df.replace(0, 1e-10)
# 执行CLR变换
geometric_mean = df.prod(axis=1) ** (1 / df.shape[1])
clr_df = np.log(df.div(geometric_mean, axis=0))
return clr_df
# 对表单2和表单3的数值列执行CLR变换
clr_sheet2 = clr_transformation(df_sheet2_numeric)
clr_sheet3 = clr_transformation(df_sheet3_numeric)
# 创建一个新的Excel文件保存变换后的数据
output_file_path = "E:/C题/2022/数据预处理后附件GPT.xlsx"
with pd.ExcelWriter(output_file_path) as writer:
clr_sheet2.to_excel(writer, sheet_name='表单2_CLR', index=False)
clr_sheet3.to_excel(writer, sheet_name='表单3_CLR', index=False)
print(f'Transformed data saved to: {output_file_path}')

二、问题一求解

1、玻璃表面风化与其类型、纹饰和颜色的关系
首先观察表单1中数据,如下图所示。除“编号”一列,纹饰、类型、颜色、表面风化四列均为定类数据。因此我们要考虑的,是分析定类数据之间关系的方法。比如卡方独立检验,Cramer的V统计量、Fisher精确检验、相关系数、logistic回归等等。

然后我们采用excel的数据透视表对表单1中数据进行特征观察,汇总列联表如像下图所示:

可以发现,样本总数均在50以上,但其中部分数据点存在0点。根据方法特征,对于样本总量>40,列联表中数据均>5的类型与表面是否风化的关系,可以采用卡方独立检验;对于列联表中部分<5数据的纹饰、颜色与表面是否分化的关系,采用Fisher-Freeman-Halton检验。
(1)检验纹饰与表面风化是否存在显著关联
#检验纹饰与表面风化是否存在显著关联
#执行Fisher-Freeman-Halton检验
import numpy as np
import statsmodels.api as sm
contingency_table = np.array([[11, 11], #列联表
[6, 0],
[17, 13]
])
table = sm.stats.Table(contingency_table)
fisher_result = table.test_nominal_association()
print(f"p值: {fisher_result.pvalue}")
alpha = 0.05 #百分之95的置信度
if fisher_result.pvalue < alpha:
print("拒绝原假设,行和列之间存在显著关联。")
else:
print("不能拒绝原假设,纹饰与表面风化没有显著关联。")运行结果如下:

(2)检验玻璃类型与表面风化是否存在显著关联
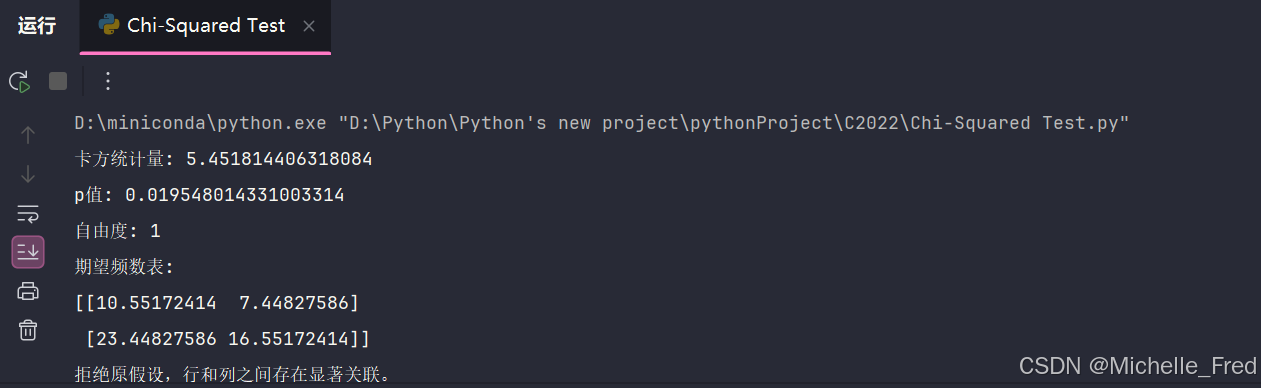
#检验玻璃类型与表面风化是否存在显著关联
#卡方检验代码
import numpy as np
from scipy.stats import chi2_contingency
observed = np.array([[6, 12], #频数表
[28, 12],
])
chi2, p, dof, expected = chi2_contingency(observed)
print(f"卡方统计量: {chi2}")
print(f"p值: {p}")
print(f"自由度: {dof}")
print(f"期望频数表:\n{expected}")
alpha = 0.05 #95%的置信度
if p < alpha:
print("拒绝原假设,行和列之间存在显著关联。")
else:
print("不能拒绝原假设,行和列之间没有显著关联。")运行结果如下:
 (3)检验颜色与表面风化是否存在显著关联
(3)检验颜色与表面风化是否存在显著关联
#检验颜色与表面风化是否存在显著关联
#执行Fisher-Freeman-Halton检验
import numpy as np
import statsmodels.api as sm
contingency_table = np.array([[2, 0], #列联表
[9, 6],
[0, 1],
[16, 8],
[1, 2],
[0, 2],
[4, 3],
[2, 2]
])
table = sm.stats.Table(contingency_table)
fisher_result = table.test_nominal_association()
print(f"p值: {fisher_result.pvalue}")
alpha = 0.05 #百分之95的置信度
if fisher_result.pvalue < alpha:
print("拒绝原假设,行和列之间存在显著关联。")
else:
print("不能拒绝原假设,颜色与表面风化没有显著关联。")
运行结果如下 :
 2、考虑玻璃类型,探究有无风化化学成分含量的统计规律
2、考虑玻璃类型,探究有无风化化学成分含量的统计规律
我们首先将表单1、表单2进行合并,并划分为以下表格:
 再通过python代码,绘制箱型图,探究有无风化化学成分含量的统计规律
再通过python代码,绘制箱型图,探究有无风化化学成分含量的统计规律
#绘制箱型图(多子图)的代码
import pandas as pd
import matplotlib.pyplot as plt
files = ["E:/C题/2022/问题1/高钾_风化.xlsx", "E:/C题/2022/问题1/高钾_无风化.xlsx", "E:/C题/2022/问题1/铅钡_风化.xlsx", "E:/C题/2022/问题1/铅钡_无风化.xlsx"]
labels = ['高钾_风化', '高钾_无风化', '铅钡_风化', '铅钡_无风化']
dfs = [pd.read_excel(file).iloc[:, 1:15] for file in files]
column_names = dfs[0].columns
plt.style.use('seaborn-darkgrid')
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 处理中文乱码问题
plt.rcParams['axes.unicode_minus'] = False # 处理坐标轴负号问题
fig, axes = plt.subplots(nrows=7, ncols=2, figsize=(15, 30))
axes = axes.flatten()
for i in range(dfs[0].shape[1]): # 假设每个文件的第2到第15列都有相同的化学成分
data = [df.iloc[:, i] for df in dfs]
ax = axes[i]
ax.boxplot(data, labels=labels)
ax.set_title(f'{column_names[i]}', fontsize=10)
ax.set_xlabel('样本分类', fontsize=10)
ax.set_ylabel('含量', fontsize=10)
#ax.tick_params(axis='x', rotation=45)
for j in range(i + 1, len(axes)):
fig.delaxes(axes[j])
plt.tight_layout()
plt.subplots_adjust(top=0.96) # 调整顶部距离以防止标题重叠
plt.show()
箱型图如下所示:
3、根据风化点数据,预测其风化前各成分含量
风化后相对成分数据+玻璃风化前后各成分相对含量均值差=预测后的数据


再通过CLR的逆转换,将CLR相对成分数据转换成原始数据,代码如下:
import pandas as pd
import numpy as np
# 读取Excel文件
file_path = "E:/C题/2022/问题1/铅钡_风化_预测无风化各项成分 - 副本.xlsx"
xls = pd.ExcelFile(file_path)
# 读取表单数据(假设表单名为'表单2_CLR'和'表单3_CLR')
clr_sheet2 = pd.read_excel(xls, 'Sheet1')
# 定义执行CLR逆变换的函数
def clr_inverse_transformation(clr_df):
exp_df = np.exp(clr_df)
original_df = exp_df.div(exp_df.sum(axis=1), axis=0)
return original_df
# 对表单2和表单3的CLR变换数据执行逆变换
original_sheet2 = clr_inverse_transformation(clr_sheet2)
# 创建一个新的Excel文件保存还原后的数据
output_file_path = "E:/C题/2022/问题1/铅钡_风化_预测无风化各项成分CLR逆转换.xlsx"
with pd.ExcelWriter(output_file_path) as writer:
original_sheet2.to_excel(writer, sheet_name='Sheet1_原成分', index=False)
print(f'Inverse transformed data saved to: {output_file_path}')


三、问题二求解

1、分析高钾玻璃、铅钡玻璃的分类规律
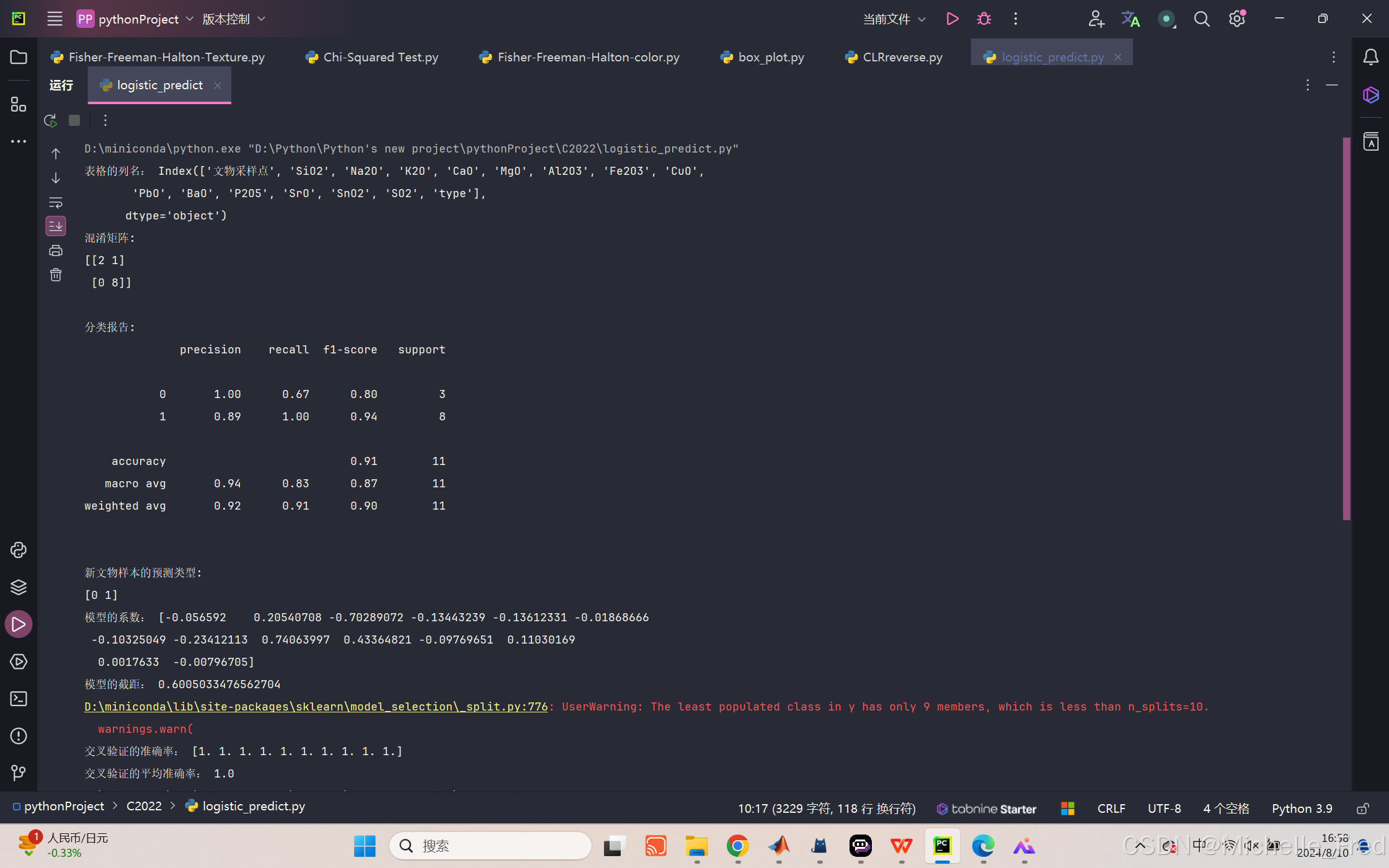
(1)Logistic回归
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, confusion_matrix
# 读取表格文件
file_path = "E:/C题/2022/问题1/无风化.xlsx" # 请替换为你的文件路径
data = pd.read_excel(file_path)
# 打印表格列名以确认列索引正确
print("表格的列名:", data.columns)
# 选择化学成分作为特征变量(第2-14列),文物样本类型作为目标变量(第15列)
X = data.iloc[:, 1:15]
y = data.iloc[:, 15]
# 将目标变量转换为二分类变量(0和1)
y = y.map({'高钾': 0, '铅钡': 1})
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# 建立二元Logistic回归模型
model = LogisticRegression()
model.fit(X_train, y_train)
# 进行预测
y_pred = model.predict(X_test)
# 输出结果
print("混淆矩阵:")
print(confusion_matrix(y_test, y_pred))
print("\n分类报告:")
print(classification_report(y_test, y_pred))
# 预测新的文物样本类型
new_samples = pd.DataFrame([
[78.45, 0.04, 0.04, 6.08, 1.86, 7.23, 2.15, 2.11, 0.04, 0.04, 1.06, 0.03, 0.04, 0.51], # 请替换为新样本的化学成分数据
[37.75, 0.04, 0.04, 7.63, 0.04, 2.33, 0.04, 0.04, 34.3, 0.04, 14.27, 0.04, 0.04, 0.04],
], columns=X.columns) # 添加列名
new_predictions = model.predict(new_samples)
print("\n新文物样本的预测类型:")
print(new_predictions)
#查看模型系数
import numpy as np
# 获取模型的系数和截距
coefficients = model.coef_[0]
intercept = model.intercept_[0]
# 输出系数和截距
print("模型的系数:", coefficients)
print("模型的截距:", intercept)
#画ROC曲线
import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, roc_auc_score
# 获取预测概率
y_proba = model.predict_proba(X_test)[:, 1]
# 计算 ROC 曲线
fpr, tpr, thresholds = roc_curve(y_test, y_proba)
roc_auc = roc_auc_score(y_test, y_proba)
# 绘制 ROC 曲线
plt.figure()
plt.plot(fpr, tpr, color='blue', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='gray', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()
#判断模型是否过拟合
from sklearn.model_selection import cross_val_score
# 在训练集上进行 10 折交叉验证
cv_scores = cross_val_score(model, X_train, y_train, cv=10, scoring='accuracy')
print("交叉验证的准确率:", cv_scores)
print("交叉验证的平均准确率:", np.mean(cv_scores))
#绘制学习曲线
from sklearn.model_selection import learning_curve
# 计算学习曲线
train_sizes, train_scores, test_scores = learning_curve(model, X, y, cv=10, n_jobs=-1, train_sizes=np.linspace(0.1, 1.0, 10))
# 计算训练和测试集的平均准确率及标准差
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)
# 绘制学习曲线
plt.figure()
plt.title("Learning Curve")
plt.xlabel("Training examples")
plt.ylabel("Score")
plt.ylim(0.7, 1.1)
# 填充区域表示标准差
plt.fill_between(train_sizes, train_scores_mean - train_scores_std, train_scores_mean + train_scores_std, alpha=0.1, color="r")
plt.fill_between(train_sizes, test_scores_mean - test_scores_std, test_scores_mean + test_scores_std, alpha=0.1, color="g")
# 绘制平均准确率曲线
plt.plot(train_sizes, train_scores_mean, 'o-', color="r", label="Training score")
plt.plot(train_sizes, test_scores_mean, 'o-', color="g", label="Cross-validation score")
plt.legend(loc="best")
plt.show()
 学习曲线如下图所示:
学习曲线如下图所示:


如上图,训练集准确率极高,验证集也随着数据量的增加而增加,但训练集始终高于验证集,因此logistic回归呈现出明显的过拟合,这也意味着样本线性可分。
(2)支持向量机(SVM)
因为我们的数据太少,所以选取适用于小样本、高维模式识别的支持向量机(SVM)。

再观察各成分分布的散点图后,我们选取氧化钡(BaO)和氧化铅(PbO)作为高钾玻璃和铅钡玻璃分类的主要依据,以下为使用matlab预测的氧化钡(BaO)和氧化铅(PbO)的分布散点图

然后我们再通过python求出氧化钡(BaO)和氧化铅(PbO)所构成的散点图分界线(SVM的核函数--线性函数)
import pandas as pd
import numpy as np
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
# 读取数据
df = pd.read_excel("E:/C题/2022/问题2/无风化.xlsx", sheet_name='Sheet1')
# 提取特征和标签
X = df[['BaO', 'PbO']].values
y = df['type'].map({'高钾': 0, '铅钡': 1}).values
# 训练SVM模型
clf = SVC(kernel='linear')
clf.fit(X, y)
# 绘制分类边界线
plt.figure(figsize=(8, 6))
plt.scatter(X[y==0, 0], X[y==0, 1], label='高钾', color='b')
plt.scatter(X[y==1, 0], X[y==1, 1], label='铅钡', color='r')
# 计算分类边界线的函数表达式
w = clf.coef_[0]
a = -w[0] / w[1]
xx = np.linspace(0, 5)
yy = a * xx - (clf.intercept_[0]) / w[1]
plt.plot(xx, yy, '-k', label='分类边界线')
plt.xlabel('BaO')
plt.ylabel('PbO')
plt.legend()
plt.grid()
plt.show()
分界线为:y = -0.5468 * x + 1.9013
当点的PbO和BaO坐标满足以下条件时,属于高钾玻璃:
y > -0.5468 * x + 1.9013
当点的PbO和BaO坐标满足以下条件时,属于铅钡玻璃:
y <= -0.5468 * x + 1.9013
具体来说:
如果一个文物样品的BaO和PbO含量位于分界线上方,则判定为高钾玻璃。
如果一个文物样品的BaO和PbO含量位于分界线及其下方,则判定为铅钡玻璃。























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








