[POJ]2299 Ultra-QuickSort

最新推荐文章于 2021-01-24 14:23:50 发布

Miner_Sty

最新推荐文章于 2021-01-24 14:23:50 发布

阅读量509

点赞数

分类专栏：算法之路文章标签： poj 算法 C++ 归并排序逆序对

本文链接：https://blog.csdn.net/Miner_Sty/article/details/50075305

版权

算法之路专栏收录该内容

10 篇文章 0 订阅

订阅专栏

[POJ]2299 Ultra-QuickSort

问题

Description

In this problem, you have to analyze a particular sorting algorithm. The algorithm processes a sequence of n distinct integers by swapping two adjacent sequence elements until the sequence is sorted in ascending order. For the input sequence 9 1 0 5 4 ,
Ultra-QuickSort produces the output 0 1 4 5 9 .
Your task is to determine how many swap operations Ultra-QuickSort needs to perform in order to sort a given input sequence.

Input

The input contains several test cases. Every test case begins with a line that contains a single integer n < 500,000 – the length of the input sequence. Each of the the following n lines contains a single integer 0 ≤ a[i] ≤ 999,999,999, the i-th input sequence element. Input is terminated by a sequence of length n = 0. This sequence must not be processed.

Output

For every input sequence, your program prints a single line containing an integer number op, the minimum number of swap operations necessary to sort the given input sequence.

Sample Input

5
9
1
0
5
4
3
1
2
3
0

Sample Output

6
0

分析

题目大意是有一种排序，只能交换相邻的数，现在要从小到大排序，请问要交换多少次。
是逆序对的变种，可以采用归并排序的思想，在归并过程中统计逆序对的数量，逆序对数量即为排序需要交换的次数。
以题中数据为例，输入9 1 0 5 4

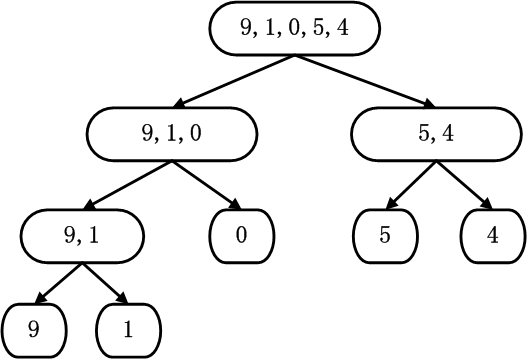
将数组自顶向下划分后

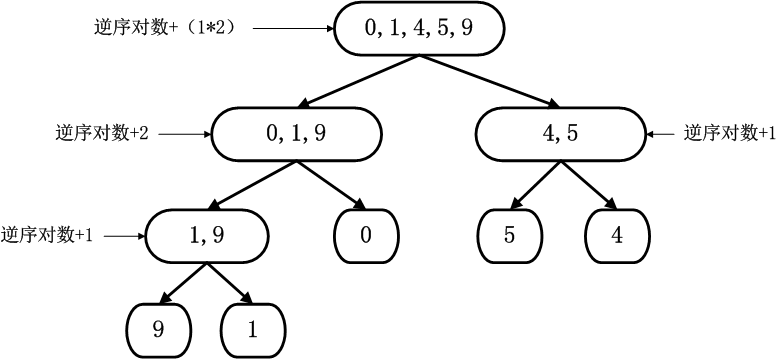
将划分后的数组自底向上归并，同时统计逆序对数。

源代码

#include <iostream>
#define MAXN 500010
using namespace std;

long long ans;
int a[MAXN], b[MAXN], c[MAXN];

void merge(int *a, int left, int mid, int right) {
    int i, j;
    i = 0;
    for (j = left; j <= mid; ++j)
        b[i++] = a[j];
    int len1 = mid - left + 1;
    i = 0;
    for (j = mid + 1; j <= right; ++j)
        c[i++] = a[j];
    int len2 = right - mid;
    i = 0, j = 0;
    int k = left;
    while (i < len1 && j < len2 && k <= right) {
        if (b[i] <= c[j])
            a[k++] = b[i++];
        else {
            a[k++] = c[j++];
            ans += (len1 - i);
        }
    }
    while (i < len1)    a[k++] = b[i++];
    while (j < len2)    a[k++] = c[j++];
}

void merge_sort(int *a, int left, int right) {
    if (left < right) {
        int mid = (left + right) / 2;
        merge_sort(a, left, mid);
        merge_sort(a, mid + 1, right);
        merge(a, left, mid, right);
    }
}

int main() {
    int N;
    while (cin >> N, N) {
        for (int i = 0; i < N; ++i)
            cin >> a[i];
        ans = 0;
        merge_sort(a, 0, N - 1);
        cout << ans << endl;
    }
    return 0;
}