【格拉霍夫定理】【四连杆系统】Grashof’s Law for a Planar Four-Bar Linkage

在《Craig, John J - Introduction to Robotics_ Mechanics and Control-Pearson (2013)》一书中提到 “a four-bar linkage has only one degree of freedom” ，即“四连杆机构只有一个自由度”。本文将从零基础开始解释此句的原因。由于自学，恐有疏漏，还望赐教。

1.What is a Planar Four-Bar Linkage? 什么是四连杆机构？

• The simplest of all closed loop mechanisms 最简单的闭环结构
• Comprises four bar-shaped links: 3 moving links, 1 fixed link and 4 pin joints 包含4个连杆，其中有3个移动连杆，1个固定连杆和4个枢接
• The four bar chain has four turning pairs 包含4个转动副

图1.1 四连杆机构示意图

2.Terminology 相关术语

• Crank：A link which can make complete revolution is known as crank. 曲柄：能作完全旋转的连杆称为曲柄。
• Rocker：Any link which does not revolve is called a rocker.
  摇杆：任何不旋转的链接都称为摇杆。
• Frame：The fixed link is known as frame.
  框架：固定链接称为框架。
• Coupler/connecting rod：The opposite link of frame is known as connecting rod.
  耦合器/连杆：框架的相对连杆称为连杆。
• Crank-rocker mechanism：In a four bar linkage, if the shorter side link revolves and the other one rocks (i.e., oscillates), it is called a crank-rocker mechanism.
  曲柄摇杆机构：在四杆连杆机构中，如果较短的侧连杆旋转而另一侧连杆摇摆（即摆动），则称为曲柄摇杆机构。如图2.1。
• Double-crank mechanism：In a four bar linkage, if both of the side links revolve, it is called a double-crank mechanism.
  双曲柄机构：在四连杆机构中，如果两个侧连杆都旋转，则称为双曲柄机构。如图2.2。
• Double-rocker mechanism：In a four bar linkage, if both of the side links rock, it is called a double-rocker mechanism.
  双摇杆机构：在四连杆机构中，如果两个侧连杆都摇动，则称为双摇杆机构。如图2.3。

图2.1 曲柄摇杆机构示意图（s+l < p+q） 图2.2 双曲柄机构示意图（s+l < p+q）

图2.3 双摇杆机构示意图（s+l < p+q）

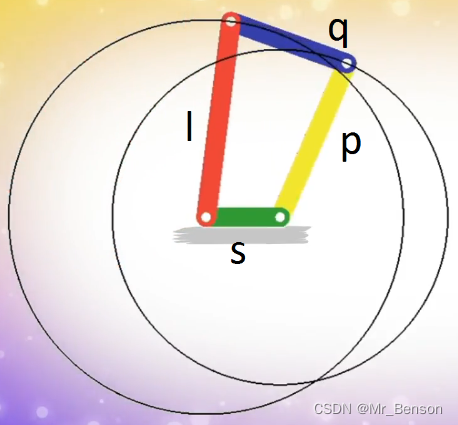
where s = length of the shortest link；l = length of the largest link；p and q = lengths of the other two links.
其中，s是最短链接的长度，l是最长链接的长度，p 和 q 是 其他两个链接的长度

3.Grashof’s Law 格拉霍夫定理

Grashof’s Law states that for a planar four-bar linkage system, the sum of the shortest and longest link lengths cannot be greater than the sum of the remaining two link lengths if there is to be a continuous relative rotation between two members.

Grashof 定律指出，对于平面四连杆系统，如果两个构件之间存在连续的相对旋转，则最短和最长连杆长度之和不能大于其余两个连杆长度之和。

在数学上表示该定理：假设 s 是最短链接的长度，l 是最长链接的长度，p 和 q 是 其他两个链接的长度，如果两个构件之间存在连续的相对旋转，则有如下公式：

$$s+l\le p+q(1)$$

Note: if s + l > p + q, then no continuous relative motion is possible; i.e., if the above inequality is NOT satisfied, no link will make a complete revolution relative to another.
需要注意的是，如果s + l > p + q，则不可能有连续的相对运动。

图3.1 不同情况的四连杆机构示意图

4.The Degree of Freedom – Definition and Calculation Method
自由度定义和计算方法（刚体、二维）

Definition : The number of independent motions that are allowed to the body or, in case of a mechanism made of several bodies, number of possible independent relative motions between the pieces of the mechanism

定义：物体允许的独立运动的数量，或者在由多个物体组成的机构的情况下，机构部件之间可能的独立相对运动的数量

For a simple mechanism, the degree of freedom (F) is given by the Grubler’s criterion: F = 3 (n - 1) - 2j - h, where j = number of revolute joints, n = number of links, h = number of higher pairs

对于简单机构，自由度 (F) 由 Grubler 准则给出：F = 3 (n - 1) - 2j - h 其中，j = 旋转关节的数量，n = 链接的数量，h = 高副的数量

在平面四杆连杆机构中，n = 4, j = 4, h = 0 ,代入公式后，得 F = 1，即自由度为1。

5.扩展连接

• Chebychev-Grübler-Kutzbach 准则
• 四连杆系统详细介绍
• Grashof’s Law for a Planar Four-Bar Linkage [PPT]
• What is Grashof’s law?