四连杆机构运动学推导

简单推了一下，然后发现没啥必要推导。毕竟花了时间，写下来聊以记录。

四连杆机构简图

本文是交叉的四连杆推导，不交叉的也是一样的，没啥区别。

为方便记录，将记为，其中，为驱动角度，在以下推导中是已知量

方法一：利用矢量闭环计算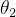和

从A出发，两个方向的矢量和同时到达C点：

等式两边的xy分量相等，有：

整理一下有：

可以使用matlab解这个方程组：

% 首先数据初始化
l0 = 5;
l1 = 10;
l2 = 5;
l3 = 10;
syms th2 th3
% 解方程
th1 = pi/3*2;
[th2, th3] = vpasolve(l2*cos(th2)-l3*cos(th3)==-l0-l1*cos(th1),...
                    l2*sin(th2)-l3*sin(th3)==-l1*sin(th1),th2,th3);

这个式子可以写成矩阵形式，并且可以进一步求导从而得到角速度之间的关系。

方法二：利用连杆长度不变计算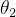

表示出D点和C点后，利用DC连杆的长度不变，可以列出等式

由，可得：

展开，并化简：

等式中，只有是未知的，其他的都是已知的，为方便计算，将已知量做以下定义：

则等式变为：，这里可以用matlab解方程得到结果，或者进一步推一下

以下计算都会涉及多解，因此sin和cos都写出来才能确定解

设：

则有：

根据反三角函数可以计算出: