原文:Ukkonen’s Suffix Tree Construction – Part 1
http://www.geeksforgeeks.org/ukkonens-suffix-tree-construction-part-1/
后缀树在很多字符串处理和计算生物学问题中是非常有用的数据结构。在很多书籍和网络资料中都有过理论上的描述,不过很少讨论过代码实现。然而,我觉得对后缀树的介绍还是不够详尽,导致在后缀树的构造和应用中,代码实现不太容易。这个系列的文章尝试建立后缀树理论与代码实现之间的桥梁。这里我们会讨论Ukkonen后缀树构造算法。我们会按照从理论到代码实现的顺序,分为多个部分进行详细介绍。首先从蛮力法开始来了解该算法中涉及的不同的概念、技巧,在最后一个部分,我们会讨论代码实现。
注意:有些部分初读的时候会不太理解,这个是很正常的,经过反复阅读和思考后这些问题都会迎刃而解。
Dan Gusfield著作的《字串,树,与序列的算法》(Algorithms on Strings, Trees and Sequences: Computer Science and Computational Biology)一书中,对相关的概念有比较详细的解释。
由m个字符组成的字符串S的后缀树T,是一个有向根树,树中恰好包含编号为1到m的m个叶子(当字符串S的最后一个字符只出现过一次的时候)。
1)根可以有零个、一个或多个孩子节点
2)每个内部节点,除了根节点意外,至少有两个孩子节点
3)每条边标记为字符串S的一个非空子串
4)从同一个节点出发的任意两条边标记的子串的首字符都不相同
从根节点到叶子节点i的路径上,所有边标记的子串联合起来构成了S的一个从位置i开始的后缀,即子串S[i...m]
注意:这里位置从1开始,而不是从0开始。(虽然这里索引不是从0开始,但是之后的代码实现过程中,我们还是从0开始索引)
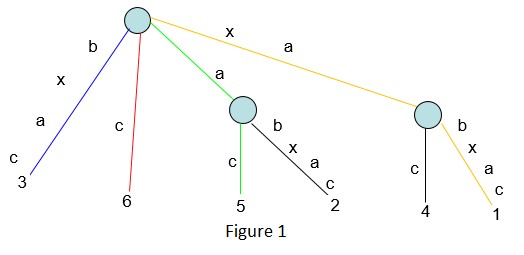
对于包含6个字符的字符串S=xabxac,它的后缀树如下图所示:
从上图可以看到,它有1个根节点,2个内部节点和6个叶节点.
红色路径的字符串深度为1,它代表从位置6开始的后缀 c
蓝色路径的字符串深度为4,它代表从位置3开始的后缀 bxac
绿色路径的字符串深度为2,它代表从位置5开始的后缀 ac
黄色路径的字符串深度为6,它代表从位置1开始的后缀 xabxac
a标签表示的边和xa标签表示的边是非叶节点边(终点是内部节点)。其他的边都是叶节点边(终点是叶节点)
如果S的一个后缀和另一个后缀的前缀匹配(当S的最后一个字符不只出现一次的时候),则前一个后缀路径的终点不是一个叶节点。
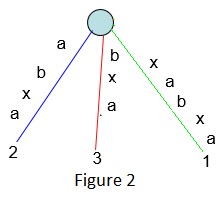
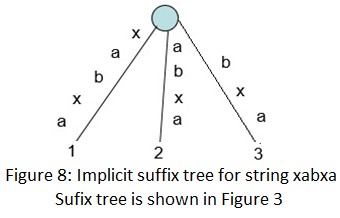
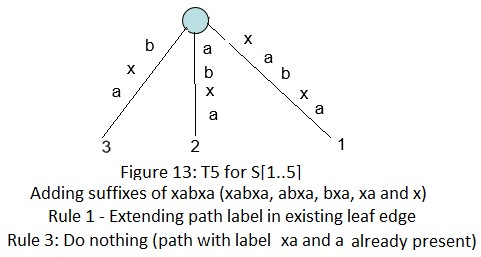
对于字符串S=xabxa,它的后缀树如下图:
这个字符串共有5个后缀:xabxa, abxa, bxa, xa 和 a.
后缀xa和a的路径的终点不是叶节点。如上图这样的树称作隐式后缀树,这是由于一些后缀(如xa和a)不能在树中显示的看到。
为了避免这个问题,我们在字符串末尾添加一个未出现过得字符。通常用$、#等字符作为终结字符。
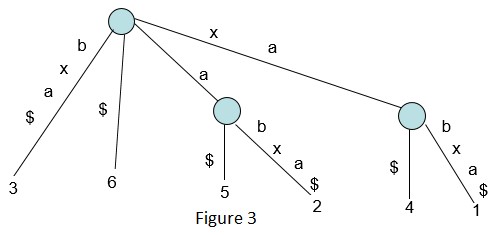
下图就是长度为6的字符串S=xabxa$的后缀树,现在它的所有后缀都在叶节点终止。
构建后缀树的一个简单的算法:
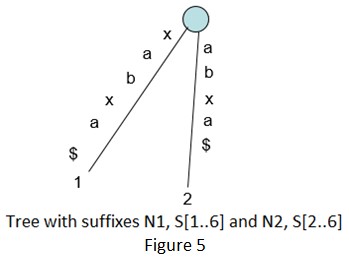
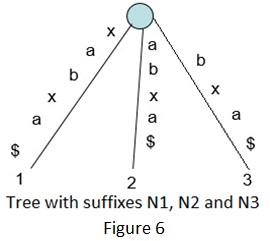
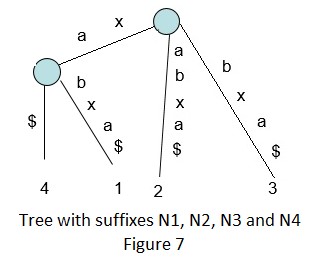
给定一个长度为m的字符串S,向树中插入一个表示后缀S[1...m]$的边,然后继续向树中插入后缀S[i...m]$表示的边,这里i从2递增到m。令Ni表示已经添加了从1到i后缀的中间状态的树,那么从Ni 构造Ni+1 的过程如下:
1)从Ni 的根节点开始搜索
2)找到从根节点开始与S[i+1 ... m]$的一个前缀匹配的最长的路径
3)上述的匹配或者终止于某个节点w,或者终止于一条边(u, v)的中间某个位置
4)如果终止于边(u, v)的中间某个位置,那么在这条边中间插入一个新的节点w,这个节点之前的边,最后一个字符与S[i+1 .. m]中的某个字符匹配,而该字符之后的一个字符是第一个与之前的边未匹配的字符。新边(u, w) 标记为与S[i+1 .. m] 匹配的部分,另一条新边(w, v)用之前的(u, v)的剩下的部分标记。
5)从节点w新建一条边(w, i+1)通向叶节点,这个边标记后缀S[i+1 .. m]未匹配的部分
用上述的算法构造长为m的字符串S的后缀树,复杂度为O(m2)
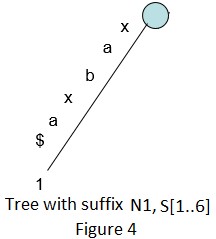
下面是基于上述算法来构建“xabxa$”字符串的后缀树的一些步骤:
隐式后缀树
当用Ukkonen算法构建后缀树的时候,我们有时候会在构建的中间过程中看到隐式后缀树,这和S中的字符有关。在隐式后缀树中,没有边包含$(或者#或者其他终止字符),而且没有只有一条出边的中间节点。
为了从S$的后缀树得到其隐式后缀树,需要如下操作
1)从后缀树的边的标签中移除所有的$标记
2)移除所有没有标签的边
3)移除所有只包含一个出边的节点,合并该节点关联的两条边
Ukkonen算法的抽象描述:
Ukkonen算法为长为m的字符串S的每个前缀S[1 .. i]构建一棵隐式后缀树。算法首先用S的第一个字符创建T1,然后用第二个字符创建T2,......,用第m个字符创建Tm。
隐式后缀树Ti+1在Ti的基础上构建。
字符串S的真正的后缀树通过在Tm的基础上加入字符$得到。
任意时刻,Ukkonen算法为当前看到的字符串构建后缀树,因此它有在线的特性,这使得它在某些场合很有用,时间复杂度为O(m)。
Ukkonen算法分为m个阶段(长为m的字符串的每个字符对应一个阶段)
在i+1阶段,基于后缀树Ti创建Ti+1。
阶段i+1又被分为i+1个扩展,这些扩展与i+1阶段的字符串S[1 .. i+1]的i+1个后缀一一对应。算法首先找到从根节点开始标签为子串S[j .. i]的路径终点。
然后在子串末尾添加字符S[i+1],用以扩展子串。
在i+1阶段的扩展1,我们在树中添加字符串S[1 .. i+1]。这时,S[i .. i]已经存在于树中,它是在i阶段添加的。我们只需要在树中添加字符S[i+1]即可。
在i+1阶段的扩展2,我们将字符串S[2 .. i+1] 添加到树中。同理,这时S[2 .. i] 已经存在于树中,我们只需要添加S[i+1]字符即可。
.
.
在i+1阶段的扩展i+1,我们将字符串S[i+1 .. i+1]添加到树中。该字符串只有一个字符,有可能没有出现在树中(如果该字符到目前为止只出现了一次)。如果该字符没在树中,我们只要添加一个标记为S[i+1]的新叶节点。
Ukkonen算法的伪码:
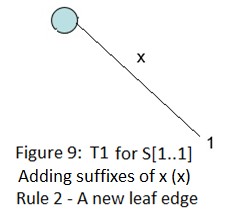
Construct tree T1
For i from 1 to m-1 do
begin {phase i+1}
For j from 1 to i+1
begin {extension j}
Find the end of the path from the root labelled S[j..i] in the current tree.
Extend that path by adding character S[i+l] if it is not there already
end;
end;
后缀扩展主要将下一个字符添加到当前构建的后缀树中。
在i+1阶段的j扩展,算法在树中找到标记为字符串S[j .. i]路径的末端,然后扩展S[j .. i],使得后缀S[j .. i+1]添加到树中。
这里共有3个扩展原则:
规则1:如果从根节点开始的标记为S[j .. i]的路径终止于叶节点边(即S[i]是叶节点边的最后一个字符),那么只要在该叶节点的标签最后添加S[i+1]字符即可。
规则2:如果从根节点开始的标记为S[j .. i]的路径终止于非叶节点边(即在该路径上S[i]字符后还有其他字符)而且下一个字符不是s[i+1],那么,创建一个新的叶节点边,标记S[i+1],和后缀起始位置j。如果路径终止于非叶节点边的中间位置,那么一个新的内部节点将被创建。
规则3:如果从根节点开始的标记为S[j .. i]的路径终止于非叶节点边(即在该路径上S[i]字符后还有其他字符)而且下一个字符是s[i+1](树中已经存在),那么什么也不做。
一个需要注意的地方是从一个给定节点(根节点或内部节点),从一个字符出发的有且只有一条边。不会有多条边从一个节点的一个字符出发。
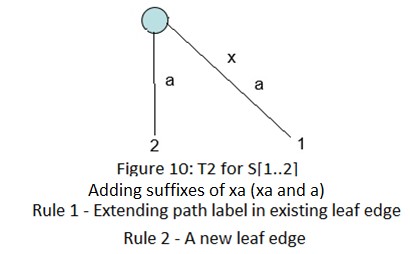
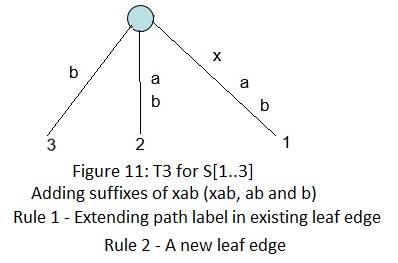
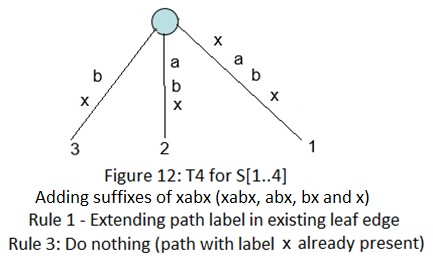
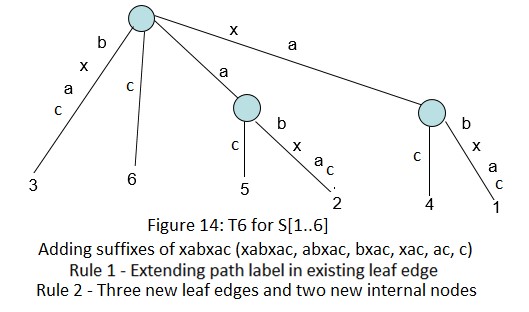
下面是字符串xabxac的后缀树用Ukkonen算法的创建过程:
在接下来的几个部分(2~6),我们会讨论后缀链接,活动节点,一些技巧和最终的代码实现。


























 1492
1492

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








