电力系统中采用三相制,因此三相变压器应用最为广泛。
重点关注三相变压器与单相变压器的区别(电路、磁路),进而去分析三相变压器所特有的联结组、不对称运行的问题。
1 三相变压器与单相变压器关系
对称运行时,三相化为一相研究。
方程式、等效电路、相量图(详见[[变压器运行方式]])仍然适用。
2 三相变压器的磁路系统
三相变压器的磁路系统可以分为各相磁路彼此无关和各相磁路彼此有关两类。
2.1 三相变压器组——各相磁路彼此无关

三相主磁通对称,三相励磁电流对称。
应用:大容量巨型变压器,运输条件受限区域
缺点:占地面积大、维护复杂、消耗材料多
2.2 三相心式变压器——各相磁路彼此有关


外加对称电压,三相主磁通对称,因此中间柱通过磁通为0,可以省略;同时为了节省硅钢片,可按图二将三相铁心布置在同一平面。
在这种布置中,每相主磁通都要借另外两相磁路闭合
造成了三相磁路长度不等(A、C长,B短),因此三相励磁电流B相较小,A、C相较大,一般忽略。
应用:电力系统中较多使用三相心式变压器
特点:占地面积小、维护方便、消耗材料少、价格便宜
3 三相变压器的电路系统——联结组问题
绕组标志
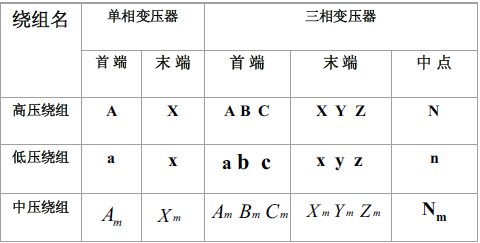
3.1 联结组
定义:根据变压器原、副边线电动势的相位关系把变压器绕组的不同联结和标号分成不同的组合,称为联结组。
同名端:任一瞬间,一个绕组的某一端的电位为正时,另一个绕组必有一个端点电位也为正,这两个对应的端点称为同名端(同极性端);即单相变压器的原、副绕组铰链着同一个主磁通
Φ
m
\varPhi_m
Φm,交变的主磁通在两个绕组产生的电动势极性相同的两端为同名端。

判断方法:
当电流从同名端流入时,产生的磁通方向一致。
同名端确定后,首、末端的标志就有两种不同的标法:
1)、同名端为首端
2)、异名端为首端
时钟表示法:把高压绕组的电动势相量看成时钟的长针,低压绕组的电动势相量看做短针。长针指到0点不动,短针所指的时数作为联结组的标号。
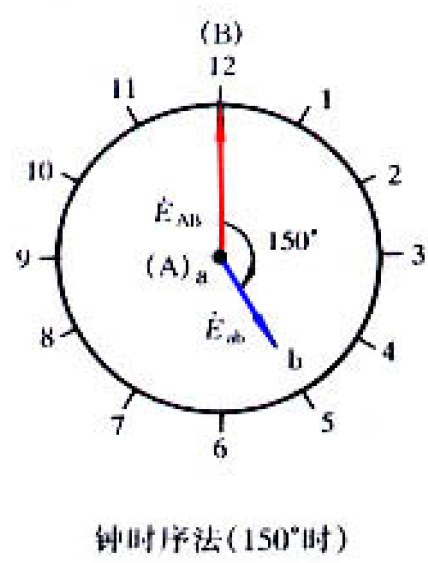
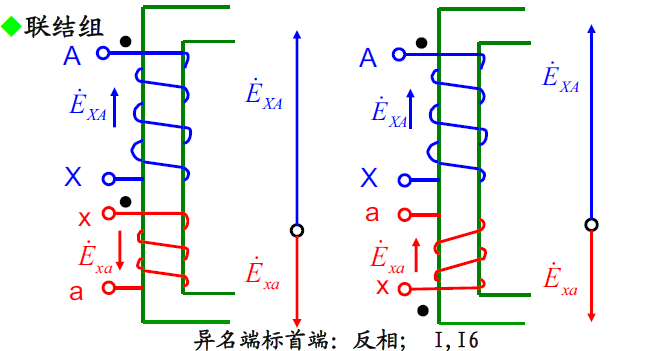
3.1.1 单相变压器联结组
单相变压器高低绕组都绕在同一铁心柱上,被同一主磁通交链。
在高低绕组中的感应电动势的相位关系只可能有两种:同相和反相
同名端标首端,同相——
I
,
I
0
I,I0
I,I0

异名端标首端,反相——
I
,
I
6
I,I6
I,I6
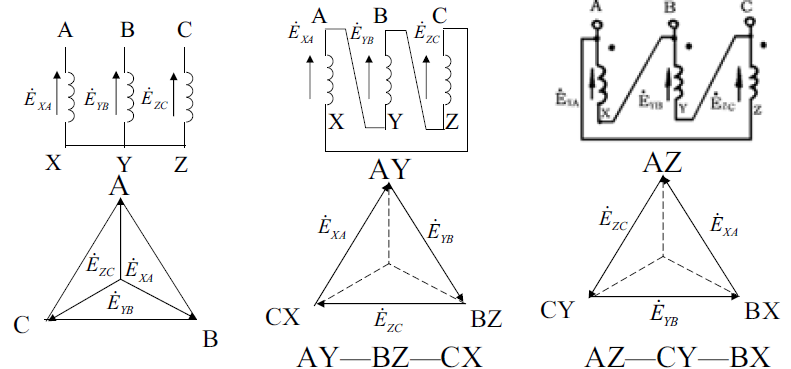
3.2.2 三相变压器联结组
三相变压器联结组不仅与绕组的绕向和首末端标志有关,而且还与三相绕组的连接方式有关。
绕组的连接方式:星形Y(Y、y)和三角形△(D、d)

相量图画法:画等边三角形顺时针标首端
线电动势三角形重心重合法:将低压边三相线电动势相量图平移到高压边三相线电动势相量图内,使两三角形重心重合。重心O到顶点A的连线为时钟的长针OA,指向0点;线段oa所指时钟序数为联结组标号。
联结组号 = E ˙ o a 滞后于 E ˙ O A 的相位角 3 0 。 联结组号=\dfrac{\dot{E}_{oa}滞后于\dot{E}_{OA}的相位角}{30^。} 联结组号=30。E˙oa滞后于E˙OA的相位角
3.2.2.1 Y,y联结
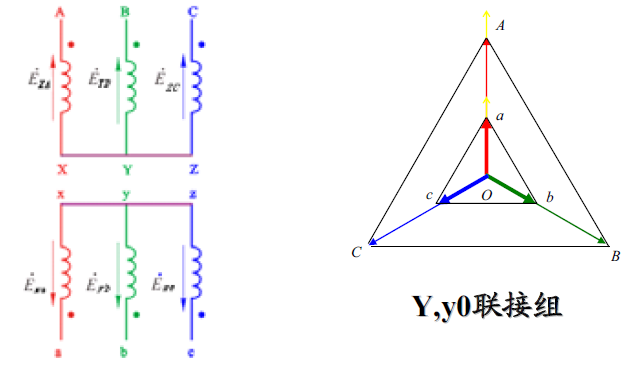

Y,y(D,d)联结方式只能得到偶数联结组:Y,y或D,d(0、2、4、6、8、10)
3.2.2.2 Y,d联结

Y,d(D,y)联结方式只能得到奇数联结组:Y,d或D,y(1、3、5、7、9、11)
总结:
按照国标只生产五种联结组:Y,yn0、Y,d11、YN,d11、YN,y0、Y,y0
Y,yn0、Y,d11、YN,d11最为常用:Y,yn0——副边可引出中线称为三相四线制,用于配电变压器可兼带照明负载和动力负载
Y,d11——用于副边电压超过400V电路中,有利于运行(谐波问题)
YN,d11——用于高压输电线路中,使电力系统高压边有可能接地
3.2 变压器空载运行电动势波形 #变压器空载运行电动势、励磁电流波形
3.2.1 单相变压器空载运行电动势波形
详见:[[变压器运行方式#1.1.1 变压器空载运行电流波形 变压器空载运行电动势、励磁电流波形]]
磁路饱和时,尖顶波励磁电流产生正弦波磁通
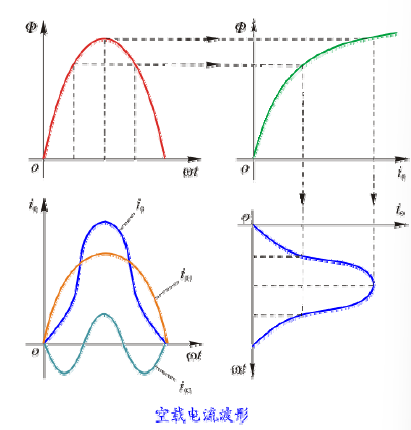
3.2.2 三相变压器空载运行电动势波形
Φ \varPhi Φ和 e e e的波形与联结组(电路系统)和磁路系统有关:
电路系统(三次谐波电流同大小、同相位)
Y接——三次谐波电流不能流通
△接——三次谐波电流能流通磁路系统
组式——三次谐波磁通能在铁心流通
心式——三次谐波磁通不能在铁心流通正弦波励磁电流 → \rightarrow →平顶波磁通(含三次谐波分量)
尖顶波电流(含三次谐波分量) → \rightarrow →正弦波磁通
3.2.2.1 Y,y联结三相变压器空载运行电动势波形
空载电流波形:
Y接,
i
03
i_{03}
i03不能流通,正弦波
主磁通波形:
正弦波励磁电流
→
\rightarrow
→平顶波磁通,此时考虑磁路,三次谐波磁通是否能流通:
三相变压器组,
Φ
3
\varPhi_3
Φ3可以流通,平顶波
三相心式变压器,
Φ
3
\varPhi_3
Φ3不能流通,正弦波
相电动势波形:
三相变压器组
三次谐波磁通沿主磁路闭合,且频率为基波的三倍
{
E
11
=
4.44
f
N
1
Φ
m
1
E
13
=
4.44
(
3
f
)
N
1
Φ
m
3
\begin{cases} E_{11}=4.44fN_1\varPhi_{m1} \\ E_{13}=4.44(3f)N_1\varPhi_{m3} \end{cases}
{E11=4.44fN1Φm1E13=4.44(3f)N1Φm3
三次谐波电动势很大(45%~60%基波)
引起相电动势波形畸变,最大值升高很多
相电动势波形畸变产生的过电压可能严重危害绝缘,三相组式变压器不能采用Y,y接
三相心式变压器
正弦波磁通
→
\rightarrow
→正弦波相电动势
三次谐波电动势沿油、邮箱壁闭合,磁阻大,引起附加涡流损耗发热,降低变压器效率
三相心式变压器可以采用Y,y接,但容量大于1800kVA时不宜采用(考虑到发热损耗)
线电动势波形:
三次谐波相电动势相互抵消,线电动势为正弦波
E
˙
A
B
=
E
˙
A
1
+
E
˙
A
3
−
E
˙
B
1
−
E
˙
B
3
=
E
˙
A
1
−
E
˙
B
1
\dot{E}_{AB}=\dot{E}_{A1}+\dot{E}_{A3}-\dot{E}_{B1}-\dot{E}_{B3}=\dot{E}_{A1}-\dot{E}_{B1}
E˙AB=E˙A1+E˙A3−E˙B1−E˙B3=E˙A1−E˙B1
总结:Y,y接线
| 磁路类型 | 空载电流 | 主磁通 | 相电动势 | 线电动势 |
|---|---|---|---|---|
| 组式 | 正弦波 | 平顶波 | 波形畸变 | 正弦波 |
| 心式 | 正弦波 | 正弦波 | 正弦波 | 正弦波 |
3.2.2.2 D,y联结三相变压器空载运行电动势波形
空载电流波形:
D接,
i
03
i_{03}
i03能流通,尖顶波
主磁通波形:
尖顶波电流(含三次谐波分量)
→
\rightarrow
→正弦波磁通,无
Φ
3
\varPhi_3
Φ3
相电动势波形:
正弦波磁通
→
\rightarrow
→正弦波相电动势
线电动势波形:
无三次谐波相电动势,线电动势为正弦波
总结:D,y接线
| 空载电流 | 主磁通 | 相电动势 | 线电动势 |
|---|---|---|---|
| 尖顶波 | 正弦波 | 正弦波 | 正弦波 |
3.2.2.3 Y,d联结三相变压器空载运行电动势波形
空载电流波形:
Y接,
i
03
i_{03}
i03不能流通,正弦波
⋆
\star
⋆主磁通波形:
应为:正弦波励磁电流
→
\rightarrow
→平顶波磁通(含三次谐波分量)
但是
Φ
3
\varPhi_3
Φ3在二次绕组中感应电动势
e
23
e_{23}
e23,并在△绕组内产生
i
23
i_{23}
i23,
i
23
i_{23}
i23产生磁通
Φ
23
\varPhi_{23}
Φ23削弱了
Φ
3
\varPhi_3
Φ3的作用,因此磁路中实际存在的三次谐波磁通及其产生的三次谐波电动势很小
→
\rightarrow
→正弦波磁通
相电动势波形:
正弦波磁通
→
\rightarrow
→正弦波相电动势
线电动势波形:
无三次谐波相电动势,线电动势为正弦波
总结:Y,d接线
| 空载电流 | 主磁通 | 相电动势 | 线电动势 |
|---|---|---|---|
| 正弦波 | 正弦波 | 正弦波 | 正弦波 |
3.2.2.4 YN,y联结三相变压器空载运行电动势波形
空载电流波形:
YN接,
i
03
i_{03}
i03能流通(通过中线),尖顶波
主磁通波形:
尖顶波电流(含三次谐波分量)
→
\rightarrow
→正弦波磁通,无
Φ
3
\varPhi_3
Φ3
相电动势波形:
正弦波磁通
→
\rightarrow
→正弦波相电动势
线电动势波形:
无三次谐波相电动势,线电动势为正弦波
总结:YN,y接线
| 空载电流 | 主磁通 | 相电动势 | 线电动势 |
|---|---|---|---|
| 尖顶波 | 正弦波 | 正弦波 | 正弦波 |
3.2.2.5 Y,yn联结三相变压器空载运行电动势波形
空载时与Y,y接线一致
负载时二次侧可为三次谐波提供通路,改善相电动势波形(由于负载影响,效果有限)。
总结:
1、 i 0 i_{0} i0中有无 i 03 i_{03} i03取决于电路,即电路联结中有无 i 03 i_{03} i03通路
Y联结——无 i 03 i_{03} i03通路 ⇒ \Rightarrow ⇒ i 0 i_{0} i0正弦波
YN或D(d)联结——有 i 03 i_{03} i03通路 ⇒ \Rightarrow ⇒ i 0 i_{0} i0尖顶波
2、 Φ \varPhi Φ中有无 Φ 3 \varPhi_3 Φ3取决于磁路,即磁路结构中有无 Φ 3 \varPhi_3 Φ3通路
三相组式变压器——有 Φ 3 \varPhi_3 Φ3通路 ⇒ \Rightarrow ⇒ Φ \varPhi Φ平顶波
三相心式变压器——无 Φ 3 \varPhi_3 Φ3通路 ⇒ \Rightarrow ⇒ Φ \varPhi Φ正弦波
3、铁心饱和时,要得到正弦波的磁通和电动势,就必须有三次谐波磁动势(如d、D绕组内部产生的,或在心式变压器中将原有的三次谐波磁动势消耗在漏磁路)或三次谐波电流(即尖顶波电流)
4、线电动势一定为正弦波,线电流中是否有三次谐波要看是否有中线
5、变压器一次侧为YN、D联结时,相电动势波形为正弦波
6、一定需要Y,y接线时,可以采取加入第三个D接线绕组改善电动势波形
| 变压器类型 | 励磁电流三次谐波 i 03 i_{03} i03 | 主磁通三次谐波 Φ 3 \varPhi_3 Φ3 | 相电动势 | 应用 |
|---|---|---|---|---|
| Y,y(心式) | 无 | 弱(漏磁路) | 正弦波 | 1800KVA以上不用 |
| Y,y(组式) | 无 | 强(主磁路) | 尖峰波 | 不用 |
| D,y(Y,d) | 有(△内部闭合 | 可忽略(△抵消) | 近似正弦波 | 可用 |
| YN,y | 有(中线) | 无 | 正弦波 | 可用 |
| Y,yn | 有(中线) | 无 | 正弦波 | 基本同Y,y;少用 |
4 变压器的不对称运行
分析方法: #对称分量法
对称分量法 :把一组不对称的三相电压或电流看成三组同频率的对称的电压或电流的叠加,后者称为前者的对称分量。

以电流为例:
任何一组不对称的三相电流
I
˙
A
\dot{I}_A
I˙A、
I
˙
B
\dot{I}_B
I˙B、
I
˙
C
\dot{I}_C
I˙C可分解出唯一的三组对称分量:
{
I
˙
A
=
I
˙
A
+
+
I
˙
A
−
+
I
˙
A
0
I
˙
B
=
I
˙
B
+
+
I
˙
B
−
+
I
˙
B
0
I
˙
C
=
I
˙
C
+
+
I
˙
C
−
+
I
˙
C
0
(1)
\tag{1} \begin{cases} \dot{I}_A=\dot{I}^+_A+\dot{I}^-_A+\dot{I}^0_A \\ \dot{I}_B=\dot{I}^+_B+\dot{I}^-_B+\dot{I}^0_B \\ \dot{I}_C=\dot{I}^+_C+\dot{I}^-_C+\dot{I}^0_C \end{cases}
⎩
⎨
⎧I˙A=I˙A++I˙A−+I˙A0I˙B=I˙B++I˙B−+I˙B0I˙C=I˙C++I˙C−+I˙C0(1)
定义旋转因子:
α
=
e
j
12
0
。
=
−
1
2
+
j
3
2
\alpha=e^{j120^。}=-\dfrac{1}{2}+j\dfrac{\sqrt{3}}{2}
α=ej120。=−21+j23 ,那么可得:
{ I ˙ B + = α 2 I ˙ A + ; I ˙ C + = α I ˙ A + I ˙ B − = α I ˙ A − ; I ˙ C − = α 2 I ˙ A − I ˙ A 0 = I ˙ B 0 = I ˙ C 0 (2) \tag{2} \begin{cases} \dot{I}^+_B=\alpha^2\dot{I}^+_A;\dot{I}^+_C=\alpha\dot{I}^+_A \\ \dot{I}^-_B=\alpha\dot{I}^-_A;\dot{I}^-_C=\alpha^2\dot{I}^-_A \\ \dot{I}^0_A=\dot{I}^0_B=\dot{I}^0_C \end{cases} ⎩ ⎨ ⎧I˙B+=α2I˙A+;I˙C+=αI˙A+I˙B−=αI˙A−;I˙C−=α2I˙A−I˙A0=I˙B0=I˙C0(2)
将式(2)带入式(1),可得:
(
I
˙
A
I
˙
B
I
˙
C
)
=
(
1
1
1
α
2
α
1
α
α
2
1
)
(
I
˙
A
+
I
˙
A
−
I
˙
A
0
)
(3)
\tag{3} \begin{pmatrix} \dot{I}_A\\ \dot{I}_B\\ \dot{I}_C\\ \end{pmatrix}= \begin{pmatrix} 1 & 1 & 1\\ \alpha^2 & \alpha & 1\\ \alpha & \alpha^2 & 1 \end{pmatrix} \begin{pmatrix} \dot{I}^+_A\\ \dot{I}^-_A\\ \dot{I}^0_A\\ \end{pmatrix}
I˙AI˙BI˙C
=
1α2α1αα2111
I˙A+I˙A−I˙A0
(3)
对上式求逆,可得:
( I ˙ A + I ˙ A − I ˙ A 0 ) = 1 3 ( 1 α α 2 1 α 2 α 1 1 1 ) ( I ˙ A I ˙ B I ˙ C ) (4) \tag{4} \begin{pmatrix} \dot{I}^+_A\\ \dot{I}^-_A\\ \dot{I}^0_A\\ \end{pmatrix}= \frac{1}{3} \begin{pmatrix} 1 & \alpha & \alpha^2\\ 1 & \alpha^2 & \alpha\\ 1 & 1 & 1 \end{pmatrix} \begin{pmatrix} \dot{I}_A\\ \dot{I}_B\\ \dot{I}_C\\ \end{pmatrix} I˙A+I˙A−I˙A0 =31 111αα21α2α1 I˙AI˙BI˙C (4)
注意:
1)、对称分量法适用于线性电路(基于叠加原理),对于非线性电系统,需经线性化处理,求得近似结果。(如对变压器激磁阻抗,通常取额定电压下的值代替)
2)、正序电流只会产生正序压降,负序电流只会产生负序压降,零序电流只会产生零序压降,所以三个分量可以单独计算。因为每一组分量都是对称的,可以用前面所讨论的分析一相的方法,这就是对称分量法的优点。
4.1 三相变压器的正、负、零序阻抗
4.1.1 正序阻抗
与变压器等效电路一致(变压器运行方式)

4.1.2 负序阻抗
对负序分量而言,其等效电路与正序没有什么不同

4.1.3 零序阻抗
零序等效电路与磁路结构和三相绕组的联接有关。
4.1.3.1 磁路结构对零序励磁阻抗的影响
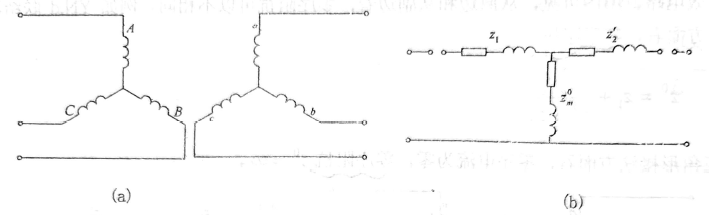
变压器零序等效电路仍用T形等效电路:
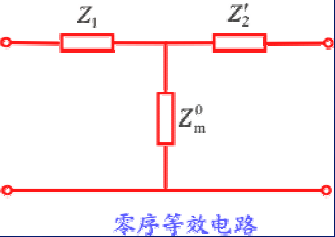
等效电路中原、副绕组的漏阻抗(
Z
1
Z_1
Z1、
Z
2
′
Z'_2
Z2′)与正序漏阻抗一致(绕组电阻与漏抗与相序无关)
零序激磁阻抗可能与正序不同,用
Z
m
0
Z^0_{m}
Zm0表示
三相组式变压器——三相磁路相互独立
零序激磁阻抗与正序激磁阻抗相等:
Z
m
0
=
Z
m
Z^0_m=Z_m
Zm0=Zm
零序电流所激励的主磁通所在磁路与正常运行时相同
三相心式变压器——三相磁路相互耦合
零序激磁阻抗远小于正序激磁阻抗:
Z
m
0
≪
Z
m
Z^0_m{\ll}Z_m
Zm0≪Zm
三相同相位的零序磁通不可能在铁心内构成闭合回路,只有从铁轭处散射出去,穿过间隙,借道油箱壁构成闭合回路,其路径与3次谐波所经路径一样(磁阻大)
4.1.3.2 不同联结方式对零序等效电路的影响
Y接——零序电流不能流通,等效电路在这一边断开
△接——零序电流仅能在三角形内部形成环流,等效电路相当于变压器内部短接,从外边看入应为开路
YN(yn)接——零序电流经中线流通,等效电路正常接入
不同联结方式的变压器零序等效电路及零序阻抗计算方式:
Y,yn:
Z
0
=
{
∞
从左侧看入
Z
2
′
+
Z
m
0
从右侧看入
Z_0= \begin{cases} \infty &\text{从左侧看入} \\ Z'_2+Z^0_m &\text{从右侧看入} \end{cases}
Z0={∞Z2′+Zm0从左侧看入从右侧看入
Y,d:
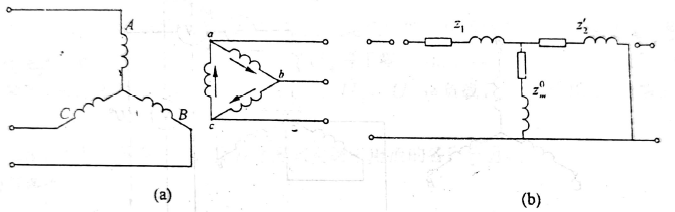
Z 0 = { ∞ 从左侧看入 ∞ 从右侧看入 Z_0= \begin{cases} \infty &\text{从左侧看入} \\ \infty &\text{从右侧看入} \end{cases} Z0={∞∞从左侧看入从右侧看入
YN,y:

Z 0 = { Z 1 + Z m 0 从左侧看入 ∞ 从右侧看入 Z_0= \begin{cases} Z_1+Z^0_m &\text{从左侧看入} \\ \infty &\text{从右侧看入} \end{cases} Z0={Z1+Zm0∞从左侧看入从右侧看入
YN,d:

Z
0
=
{
Z
1
+
Z
0
Z
2
′
Z
m
0
+
Z
2
′
从左侧看入
∞
从右侧看入
Z_0= \begin{cases} Z_1+\dfrac{Z^0Z'_2}{Z^0_m+Z'_2} &\text{从左侧看入} \\ \infty &\text{从右侧看入} \end{cases}
Z0=⎩
⎨
⎧Z1+Zm0+Z2′Z0Z2′∞从左侧看入从右侧看入
Y,y:
Z
0
=
{
∞
从左侧看入
∞
从右侧看入
Z_0= \begin{cases} \infty &\text{从左侧看入} \\ \infty &\text{从右侧看入} \end{cases}
Z0={∞∞从左侧看入从右侧看入
总结:
1、零序分量电流三相同相,其流经变压器的情况与变压器的连接方法有关:
①Y,y;Y,d;D,y;D,d连接无零序电流;
②YN,d;D,yn连接零序电流在双侧绕组内均可流通;
③YN,y;Y,yn连接零序电流只能在YN、yn侧流通。2、在零序电流可以流通的连接组中,其零序阻抗的大小还与变压器的磁路结构有关。
4.2 例:Y,yn联结三相变压器带单相负载

4.2.1运行分析
二次侧电流为:
I
˙
a
=
I
˙
I
˙
b
=
I
˙
c
=
0
\begin{alignedat}{2} \dot{I}_a&=\dot{I} \\ \dot{I}_b&=\dot{I}_c=0 \end{alignedat}
I˙aI˙b=I˙=I˙c=0
由4 变压器的不对称运行中式(4)可知:
I
˙
a
+
=
I
˙
a
−
=
I
˙
a
0
=
I
˙
3
(5)
\tag{5}\dot{I}^+_a=\dot{I}^-_a=\dot{I}^0_a=\dfrac{\dot{I}}{3}
I˙a+=I˙a−=I˙a0=3I˙(5)
各序等效电路为:

由电流关系,可将三序等效电路串联:

由等效电路,可知二次侧电压为:
{
U
˙
a
+
=
−
U
˙
A
+
−
I
˙
a
+
Z
k
正序
U
˙
a
−
=
U
˙
A
−
−
I
˙
a
−
Z
k
=
−
I
˙
a
−
Z
k
负序
U
˙
a
0
=
−
I
˙
a
0
(
Z
2
′
+
Z
m
0
)
零序
(6)
\tag{6}\begin{cases} \dot{U}^+_a&=-\dot{U}^+_A-\dot{I}^+_aZ_k &\text{ 正序} \\ \dot{U}^-_a&=\dot{U}^-_A-\dot{I}^-_aZ_k=-\dot{I}^-_aZ_k &\text{ 负序} \\ \dot{U}^0_a&=-\dot{I}^0_a(Z'_2+Z^0_m) &\text{ 零序} \end{cases}
⎩
⎨
⎧U˙a+U˙a−U˙a0=−U˙A+−I˙a+Zk=U˙A−−I˙a−Zk=−I˙a−Zk=−I˙a0(Z2′+Zm0) 正序 负序 零序(6)
在负载
Z
L
Z_L
ZL上叠加各相序电压,得到负载两端实际电压:
U
˙
a
=
U
˙
a
+
+
U
˙
a
−
+
U
˙
a
0
=
I
˙
Z
L
=
3
I
˙
a
+
Z
L
(7)
\tag{7} \begin{alignedat}{2} \dot{U}_a&=\dot{U}^+_a+\dot{U}^-_a+\dot{U}^0_a \\ &=\dot{I}Z_L=3\dot{I}^+_aZ_L \end{alignedat}
U˙a=U˙a++U˙a−+U˙a0=I˙ZL=3I˙a+ZL(7)
将式(6)带入式(7),可得:
U
˙
a
=
U
˙
A
+
−
I
˙
a
+
Z
k
−
I
˙
a
−
Z
k
−
I
˙
a
0
(
Z
2
′
+
Z
m
0
)
\dot{U}_a=\dot{U}^+_A-\dot{I}^+_aZ_k-\dot{I}^-_aZ_k-\dot{I}^0_a(Z'_2+Z^0_m)
U˙a=U˙A+−I˙a+Zk−I˙a−Zk−I˙a0(Z2′+Zm0)
将(5)(7)式带入上式,可得:
I
˙
a
+
=
U
˙
A
+
3
Z
L
+
2
Z
k
+
Z
2
′
+
Z
m
0
\dot{I}^+_a=\dfrac{\dot{U}^+_A}{3Z_L+2Z_k+Z'_2+Z^0_m}
I˙a+=3ZL+2Zk+Z2′+Zm0U˙A+
考虑到
I
˙
=
3
I
˙
a
+
\dot{I}=3\dot{I}^+_a
I˙=3I˙a+,且忽略绕组漏抗,可得:
I
˙
=
U
˙
A
+
Z
L
+
1
3
Z
m
0
\dot{I}=\dfrac{\dot{U}^+_A}{Z_L+\dfrac{1}{3}Z^0_m}
I˙=ZL+31Zm0U˙A+
此时考虑磁路系统对
Z
m
0
Z^0_m
Zm0的影响:
三相组式变压器——
Z
m
0
=
Z
m
Z^0_m=Z_m
Zm0=Zm
单相稳态短路时(
Z
L
=
0
Z_L=0
ZL=0)
I
˙
k
≈
3
U
˙
A
+
Z
m
=
3
I
˙
m
\dot{I}_k\approx\dfrac{3\dot{U}^+_A}{Z_m}=3\dot{I}_m
I˙k≈Zm3U˙A+=3I˙m
单相稳态短路电流只有正序激磁电流(很小)的三倍——正常运行更小
因此Y,yn联结的三相变压器组不能带单相到中线的不对称负载
三相心式变压器—— Z m 0 ≪ Z m Z^0_m{\ll}Z_m Zm0≪Zm
负载电流主要由负载阻抗 Z L Z_L ZL决定
因此Y,yn联结的三相心式变压器可以带单相到中线的不对称负载
4.2.2中点位移
由等效电路可知,一次侧各序电流为:
{
I
˙
A
+
≈
I
˙
a
+
正序
I
˙
A
−
≈
I
˙
a
−
负序
I
˙
A
0
=
0
零序
\begin{cases} \dot{I}^+_A&\approx\dot{I}^+_a &\text{ 正序} \\ \dot{I}^-_A&\approx\dot{I}^-_a &\text{ 负序} \\ \dot{I}^0_A&=0 &\text{ 零序} \end{cases}
⎩
⎨
⎧I˙A+I˙A−I˙A0≈I˙a+≈I˙a−=0 正序 负序 零序
由4 变压器的不对称运行中(3)式可得一次侧各相电流:
{
I
˙
A
=
I
˙
A
+
+
I
˙
A
−
≈
2
3
I
˙
I
˙
B
=
α
2
I
˙
A
+
+
α
I
˙
A
−
≈
−
1
3
I
˙
I
˙
C
=
α
I
˙
A
+
+
α
2
I
˙
A
−
≈
−
1
3
I
˙
\begin{cases} \dot{I}_A=\dot{I}^+_A+\dot{I}^-_A\approx\dfrac{2}{3}\dot{I} \\ \dot{I}_B=\alpha^2\dot{I}^+_A+\alpha\dot{I}^-_A\approx-\dfrac{1}{3}\dot{I} \\ \dot{I}_C=\alpha\dot{I}^+_A+\alpha^2\dot{I}^-_A\approx-\dfrac{1}{3}\dot{I} \end{cases}
⎩
⎨
⎧I˙A=I˙A++I˙A−≈32I˙I˙B=α2I˙A++αI˙A−≈−31I˙I˙C=αI˙A++α2I˙A−≈−31I˙
忽略绕组励磁支路与漏抗压降:
{
U
˙
a
+
=
−
U
˙
A
+
正序
U
˙
a
−
=
0
负序
U
˙
a
0
=
−
I
˙
a
0
Z
m
0
=
E
˙
a
0
零序
(8)
\tag{8}\begin{cases} \dot{U}^+_a&=-\dot{U}^+_A &\text{ 正序} \\ \dot{U}^-_a&=0 &\text{ 负序} \\ \dot{U}^0_a&=-\dot{I}^0_aZ^0_m=\dot{E}^0_a &\text{ 零序} \end{cases}
⎩
⎨
⎧U˙a+U˙a−U˙a0=−U˙A+=0=−I˙a0Zm0=E˙a0 正序 负序 零序(8)
此时
U
˙
a
=
−
U
˙
A
+
−
I
˙
a
0
Z
m
0
=
−
U
˙
A
+
+
E
˙
a
0
\dot{U}_a=-\dot{U}^+_A-\dot{I}^0_aZ^0_m=-\dot{U}^+_A+\dot{E}^0_a
U˙a=−U˙A+−I˙a0Zm0=−U˙A++E˙a0
同理可得,一次侧各相电压:
{
U
˙
A
=
U
˙
A
+
+
U
˙
A
−
+
U
˙
A
0
=
U
˙
A
+
+
1
3
I
˙
Z
m
0
U
˙
B
=
U
˙
B
+
+
1
3
I
˙
Z
m
0
U
˙
C
=
U
˙
C
+
+
1
3
I
˙
Z
m
0
\begin{cases} \dot{U}_A=\dot{U}^+_A+\dot{U}^-_A+\dot{U}^0_A= \dot{U}^+_A+\dfrac{1}{3}\dot{I}Z^0_m \\ \dot{U}_B=\dot{U}^+_B+\dfrac{1}{3}\dot{I}Z^0_m \\ \dot{U}_C=\dot{U}^+_C+\dfrac{1}{3}\dot{I}Z^0_m \end{cases}
⎩
⎨
⎧U˙A=U˙A++U˙A−+U˙A0=U˙A++31I˙Zm0U˙B=U˙B++31I˙Zm0U˙C=U˙C++31I˙Zm0
带入式(8)可得:
U
˙
a
=
U
˙
a
+
+
U
˙
a
−
+
U
˙
a
0
=
−
(
U
˙
A
+
+
I
˙
a
0
Z
m
0
)
=
−
U
˙
A
\dot{U}_a=\dot{U}^+_a+\dot{U}^-_a+\dot{U}^0_a=-(\dot{U}^+_A+\dot{I}^0_aZ^0_m)=-\dot{U}_A
U˙a=U˙a++U˙a−+U˙a0=−(U˙A++I˙a0Zm0)=−U˙A
同理:
{
U
˙
A
=
−
U
˙
a
U
˙
B
=
−
U
˙
b
U
˙
C
=
−
U
˙
c
\begin{cases} \dot{U}_A=-\dot{U}_a \\ \dot{U}_B=-\dot{U}_b \\ \dot{U}_C=-\dot{U}_c \end{cases}
⎩
⎨
⎧U˙A=−U˙aU˙B=−U˙bU˙C=−U˙c
因此可得相量图如下:

采用Y,yn联结的变压器,原边无零序电流,因此副边零序电流全部为激磁性质电流
从而在铁心内产生了零序主磁通
Φ
0
\varPhi_0
Φ0,感应零序电动势
E
a
0
E^0_a
Ea0、
E
b
0
E^0_b
Eb0、
E
c
0
E^0_c
Ec0叠加到正序电动势上
从而使带负载端的电压下降;其余两端电压上升,以保持线电压不变
三相变压器组——零序主磁通可在主磁路内通过
零序磁通和电动势较大,使得带负载相电压急剧下降,以至于无法带负载,产生严重的中性点位移现象三相心式变压器——零序磁通被迫沿油和油箱壁闭合
零序磁通和电动势较小,中性点位移不严重,可以正常运行;
为了减少零序磁通沿油和油箱壁闭合产生的涡流损耗,以及减少电压变化,Y,yn联结心式变压器中线电流( 3 I 0 3I_0 3I0)不得超过额定电流的25%。
因此,可总结出现严重中点偏移的条件:
1、一边有零序电流,另一边没有 ⇒ \Rightarrow ⇒零序激磁电流 ⇒ \Rightarrow ⇒零序磁通
2、 Z m 0 Z^0_m Zm0较大 ⇒ \Rightarrow ⇒产生较大零序电动势 E ˙ 0 \dot{E}_0 E˙0
对于线-线间不对称负载,各种联结的变压器均不产生零序电流,也就不会有严重的中点偏移(不对称现象)


























 2755
2755

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








