一、k-means聚类
指定最后聚成的簇的数目,比如,将1000人聚成5组
二、层次聚类
不需要指定最终聚成的簇的数目。取而代之的是,算法一开始将每个实例看成一个簇,然后在算法的每次迭代中都将最相似的两个簇合并在一起,该过程不断重复直到只剩下一个簇为止。
三、单连接聚类
两个簇的距离定义为一个簇的所有成员到另一个簇的所有成员之间最短的那个距离。
四、全连接聚类
两个簇的距离定义为一个簇的所有成员到另一个簇的所有成员之间最长的那个距离
五、平均连接聚类
两个簇的距离定义为一个簇的所有成员到另一个簇的所有成员之间的平均距离
六、编程实现一个层次聚类算法
from queue import PriorityQueue
import math
"""
Example code for hierarchical clustering
"""
def getMedian(alist):
"""get median value of list alist"""
tmp = list(alist)
tmp.sort()
alen = len(tmp)
if (alen % 2) == 1:
return tmp[alen // 2]
else:
return (tmp[alen // 2] + tmp[(alen // 2) - 1]) / 2
def normalizeColumn(column):
"""Normalize column using Modified Standard Score"""
median = getMedian(column)
asd = sum([abs(x - median) for x in column]) / len(column)
result = [(x - median) / asd for x in column]
return result
class hClusterer:
""" this clusterer assumes that the first column of the data is a label
not used in the clustering. The other columns contain numeric data"""
def __init__(self, filename):
file = open(filename)
self.data = {}
self.counter = 0
self.queue = PriorityQueue()
lines = file.readlines()
file.close()
header = lines[0].split(',')
self.cols = len(header)
self.data = [[] for i in range(len(header))]
for line in lines[1:]:
cells = line.split(',')
toggle = 0
for cell in range(self.cols):
if toggle == 0:
self.data[cell].append(cells[cell])
toggle = 1
else:
self.data[cell].append(float(cells[cell]))
# now normalize number columns (that is, skip the first column)
for i in range(1, self.cols):
self.data[i] = normalizeColumn(self.data[i])
###
### I have read in the data and normalized the
### columns. Now for each element i in the data, I am going to
### 1. compute the Euclidean Distance from element i to all the
### other elements. This data will be placed in neighbors,
### which is a Python dictionary. Let's say i = 1, and I am
### computing the distance to the neighbor j and let's say j
### is 2. The neighbors dictionary for i will look like
### {2: ((1,2), 1.23), 3: ((1, 3), 2.3)... }
###
### 2. find the closest neighbor
###
### 3. place the element on a priority queue, called simply queue,
### based on the distance to the nearest neighbor (and a counter
### used to break ties.
# now push distances on queue
rows = len(self.data[0])
for i in range(rows):
minDistance = 99999
nearestNeighbor = 0
neighbors = {}
for j in range(rows):
if i != j:
dist = self.distance(i, j)
if i < j:
pair = (i,j)
else:
pair = (j,i)
neighbors[j] = (pair, dist)
if dist < minDistance:
minDistance = dist
nearestNeighbor = j
nearestNum = j
# create nearest Pair
if i < nearestNeighbor:
nearestPair = (i, nearestNeighbor)
else:
nearestPair = (nearestNeighbor, i)
# put instance on priority queue
self.queue.put((minDistance, self.counter,
[[self.data[0][i]], nearestPair, neighbors]))
self.counter += 1
def distance(self, i, j):
sumSquares = 0
for k in range(1, self.cols):
sumSquares += (self.data[k][i] - self.data[k][j])**2
return math.sqrt(sumSquares)
def cluster(self):
done = False
while not done:
topOne = self.queue.get()
nearestPair = topOne[2][1]
if not self.queue.empty():
nextOne = self.queue.get()
nearPair = nextOne[2][1]
tmp = []
##
## I have just popped two elements off the queue,
## topOne and nextOne. I need to check whether nextOne
## is topOne's nearest neighbor and vice versa.
## If not, I will pop another element off the queue
## until I find topOne's nearest neighbor. That is what
## this while loop does.
##
while nearPair != nearestPair:
tmp.append((nextOne[0], self.counter, nextOne[2]))
self.counter += 1
nextOne = self.queue.get()
nearPair = nextOne[2][1]
##
## this for loop pushes the elements I popped off in the
## above while loop.
##
for item in tmp:
self.queue.put(item)
if len(topOne[2][0]) == 1:
item1 = topOne[2][0][0]
else:
item1 = topOne[2][0]
if len(nextOne[2][0]) == 1:
item2 = nextOne[2][0][0]
else:
item2 = nextOne[2][0]
## curCluster is, perhaps obviously, the new cluster
## which combines cluster item1 with cluster item2.
curCluster = (item1, item2)
## Now I am doing two things. First, finding the nearest
## neighbor to this new cluster. Second, building a new
## neighbors list by merging the neighbors lists of item1
## and item2. If the distance between item1 and element 23
## is 2 and the distance betweeen item2 and element 23 is 4
## the distance between element 23 and the new cluster will
## be 2 (i.e., the shortest distance).
##
minDistance = 99999
nearestPair = ()
nearestNeighbor = ''
merged = {}
nNeighbors = nextOne[2][2]
for (key, value) in topOne[2][2].items():
if key in nNeighbors:
if nNeighbors[key][1] < value[1]:
dist = nNeighbors[key]
else:
dist = value
if dist[1] < minDistance:
minDistance = dist[1]
nearestPair = dist[0]
nearestNeighbor = key
merged[key] = dist
if merged == {}:
return curCluster
else:
self.queue.put( (minDistance, self.counter,
[curCluster, nearestPair, merged]))
self.counter += 1
def printDendrogram(T, sep=3):
"""Print dendrogram of a binary tree. Each tree node is represented by a
length-2 tuple. printDendrogram is written and provided by David Eppstein
2002. Accessed on 14 April 2014:
http://code.activestate.com/recipes/139422-dendrogram-drawing/ """
def isPair(T):
return type(T) == tuple and len(T) == 2
def maxHeight(T):
if isPair(T):
h = max(maxHeight(T[0]), maxHeight(T[1]))
else:
h = len(str(T))
return h + sep
activeLevels = {}
def traverse(T, h, isFirst):
if isPair(T):
traverse(T[0], h-sep, 1)
s = [' ']*(h-sep)
s.append('|')
else:
s = list(str(T))
s.append(' ')
while len(s) < h:
s.append('-')
if (isFirst >= 0):
s.append('+')
if isFirst:
activeLevels[h] = 1
else:
del activeLevels[h]
A = list(activeLevels)
A.sort()
for L in A:
if len(s) < L:
while len(s) < L:
s.append(' ')
s.append('|')
print (''.join(s))
if isPair(T):
traverse(T[1], h-sep, 0)
traverse(T, maxHeight(T), -1)
filename = '//Users/raz/Dropbox/guide/data/dogs.csv'
hg = hClusterer(filename)
cluster = hg.cluster()
printDendrogram(cluster)
七、试试看
该数据集从卡内基梅隆大学(CMU)下载,地址为:http://lib.stat.cmu.edu/DASL/Datafiles/Ceraals.html
k-means聚类是最流行的聚类算法的
1、选择k个随机实例作为初始中心点;
2、REPEAT
3、将每个实例分配给最近的中心点从而形成k个簇;
4、通过计算每个簇的平均点来更新中心点
5、UNTIL中心点不再改变或改变不大
先放一下k-means聚类
爬山法
无法保证会达到全局最优的结果
SSE或散度
为度量某个簇集合的质量,我们使用误差平方和(sum of the squared error)或者称为散度的指标
其计算过程如下:对每个点,计算它到属于它的中心点之间的距离平方,然后将这些距离平方加起来求和
假定我们在同一数据集上运行两次k-means算法,每次选择的随机初始点不同。那么是第一次还是第二次得到的结果更好呢?为回答这个问题,我们计算两次聚类结果的SSE值,结果显示SSE值小的那个结果更好。
以下开始k-means
import math
import random
"""
Implementation of the K-means algorithm
for the book A Programmer's Guide to Data Mining"
http://www.guidetodatamining.com
"""
def getMedian(alist):
"""get median of list"""
tmp = list(alist)
tmp.sort()
alen = len(tmp)
if (alen % 2) == 1:
return tmp[alen // 2]
else:
return (tmp[alen // 2] + tmp[(alen // 2) - 1]) / 2
def normalizeColumn(column):
"""normalize the values of a column using Modified Standard Score
that is (each value - median) / (absolute standard deviation)"""
median = getMedian(column)
asd = sum([abs(x - median) for x in column]) / len(column)
result = [(x - median) / asd for x in column]
return result
class kClusterer:
""" Implementation of kMeans Clustering
This clusterer assumes that the first column of the data is a label
not used in the clustering. The other columns contain numeric data
"""
def __init__(self, filename, k):
""" k is the number of clusters to make
This init method:
1. reads the data from the file named filename
2. stores that data by column in self.data
3. normalizes the data using Modified Standard Score
4. randomly selects the initial centroids
5. assigns points to clusters associated with those centroids
"""
file = open(filename)
self.data = {}
self.k = k
self.counter = 0
self.iterationNumber = 0
# used to keep track of % of points that change cluster membership
# in an iteration
self.pointsChanged = 0
# Sum of Squared Error
self.sse = 0
#
# read data from file
#
lines = file.readlines()
file.close()
header = lines[0].split(',')
self.cols = len(header)
self.data = [[] for i in range(len(header))]
# we are storing the data by column.
# For example, self.data[0] is the data from column 0.
# self.data[0][10] is the column 0 value of item 10.
for line in lines[1:]:
cells = line.split(',')
toggle = 0
for cell in range(self.cols):
if toggle == 0:
self.data[cell].append(cells[cell])
toggle = 1
else:
self.data[cell].append(float(cells[cell]))
self.datasize = len(self.data[1])
self.memberOf = [-1 for x in range(len(self.data[1]))]
#
# now normalize number columns
#
for i in range(1, self.cols):
self.data[i] = normalizeColumn(self.data[i])
# select random centroids from existing points
random.seed()
self.centroids = [[self.data[i][r] for i in range(1, len(self.data))]
for r in random.sample(range(len(self.data[0])),
self.k)]
self.assignPointsToCluster()
def updateCentroids(self):
"""Using the points in the clusters, determine the centroid
(mean point) of each cluster"""
members = [self.memberOf.count(i) for i in range(len(self.centroids))]
self.centroids = [[sum([self.data[k][i]
for i in range(len(self.data[0]))
if self.memberOf[i] == centroid])/members[centroid]
for k in range(1, len(self.data))]
for centroid in range(len(self.centroids))]
def assignPointToCluster(self, i):
""" assign point to cluster based on distance from centroids"""
min = 999999
clusterNum = -1
for centroid in range(self.k):
dist = self.euclideanDistance(i, centroid)
if dist < min:
min = dist
clusterNum = centroid
# here is where I will keep track of changing points
if clusterNum != self.memberOf[i]:
self.pointsChanged += 1
# add square of distance to running sum of squared error
self.sse += min**2
return clusterNum
def assignPointsToCluster(self):
""" assign each data point to a cluster"""
self.pointsChanged = 0
self.sse = 0
self.memberOf = [self.assignPointToCluster(i)
for i in range(len(self.data[1]))]
def euclideanDistance(self, i, j):
""" compute distance of point i from centroid j"""
sumSquares = 0
for k in range(1, self.cols):
sumSquares += (self.data[k][i] - self.centroids[j][k-1])**2
return math.sqrt(sumSquares)
def kCluster(self):
"""the method that actually performs the clustering
As you can see this method repeatedly
updates the centroids by computing the mean point of each cluster
re-assign the points to clusters based on these new centroids
until the number of points that change cluster membership is less than 1%.
"""
done = False
while not done:
self.iterationNumber += 1
self.updateCentroids()
self.assignPointsToCluster()
#
# we are done if fewer than 1% of the points change clusters
#
if float(self.pointsChanged) / len(self.memberOf) < 0.01:
done = True
print("Final SSE: %f" % self.sse)
def showMembers(self):
"""Display the results"""
for centroid in range(len(self.centroids)):
print ("\n\nClass %i\n========" % centroid)
for name in [self.data[0][i] for i in range(len(self.data[0]))
if self.memberOf[i] == centroid]:
print (name)
##
## RUN THE K-MEANS CLUSTERER ON THE DOG DATA USING K = 3
###
# change the path in the following to match where dogs.csv is on your machine
km = kClusterer('../../data/dogs.csv', 3)
km.kCluster()
km.showMembers()
试试看更多的数据集








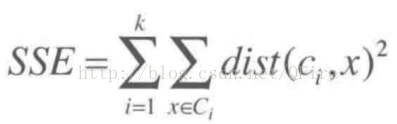














 4136
4136

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








