苔藓生长优化算法(MGO)-2024年9月SCI新算法-公式原理详解 Matlab代码免费获取

        声明：文章是从本人公众号中复制而来，因此，想最新最快了解各类智能优化算法及其改进的朋友，可关注我的公众号：强盛机器学习，不定期会有很多免费代码分享~

目录

原理简介

一、确定风向

二、孢子散布搜索

三、双传播搜索

四、隐生机制

算法流程图和伪代码

性能测评

参考文献

完整代码

---

苔藓生长优化算法(Moss Growth Optimization, MGO)是一种新型的元启发式算法（智能优化算法），灵感来源于自然环境中苔藓的生长过程。不同于以往的动物园算法，该算法采用了种群划分的方法，也有一些与以往算法不同新的机制值得我们学习，可以一试！该成果由Boli Zheng于2024年9月发表在SCI二区期刊《Journal of Computational Design and Engineering》上！

由于发表时间较短，谷歌学术上还没人引用！你先用，你就是创新！

原理简介

灵感：苔藓是地球上最古老的陆地植物之一。它通常生长在潮湿和阴凉的地方；然而，它在不同的环境中显示了弹性，从树木繁茂的地区到大都市地区。尽管没有花、果实、种子、根或真正的脉管系统，这种植物依靠独特的繁殖机制。具体来说，它们有三种繁殖方式：无性繁殖、有性繁殖和营养繁殖。此外，隐生是一种重要的生存策略，有助于物种的延续。

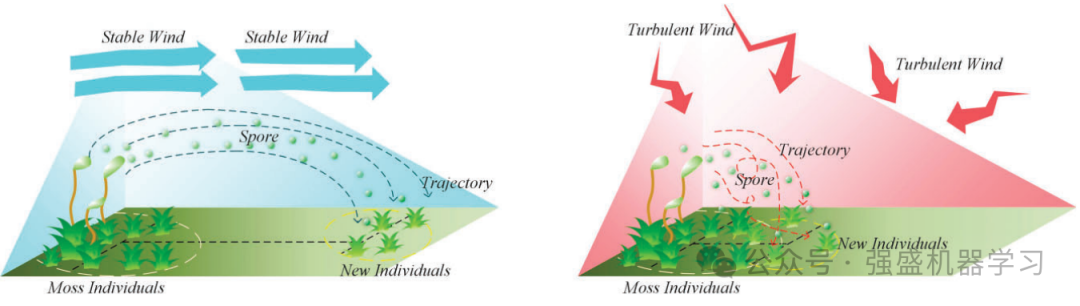
一、确定风向

MGO开发了一种创造性的机制，称为“确定风向”。这种机制利用大多数个体与最优个体之间的位置关系来确定种群中所有个体的进化方向。这种演化方向有效地避免了MGO陷入局部最优解。需要注意的是，MGO算法将单个苔藓个体作为搜索代理m，该算法的种群X由所有苔藓个体组成。本文利用MGO算法所做的如下假设来模拟风向：

(1)在整个迭代过程中，风向保持不变。

(2)假设苔藓个体代表解空间中的位置，当前最佳候选位置对应于最优解中当前苔藓个体。

(3)风的方向总是从苔藓数量较多的地区吹向最有利生长环境中的单个苔藓。

种群X中最特殊的个体是Mbest。本文采用Mbest的j维值作为阈值，并与所有个体的j维值进行比较，如式(1)所示：

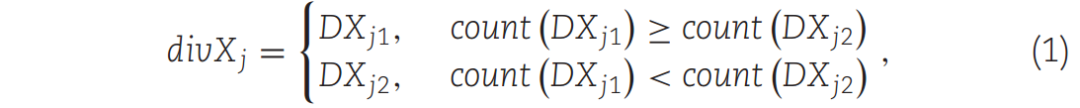
其中函数count（·）表示计算给定集合集合中苔藓个体的数量。

多次除法后得到的集合见式(2)：

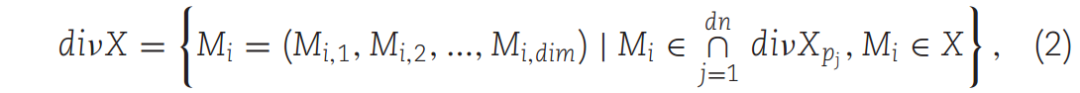
式中，dn为要被分割的次数，本文设dn的值为[dim/4]且不小于1。[·]为所填数的底函数。Pj表示第j个随机数，满足范围(1,2,…, dim)和式(3)：

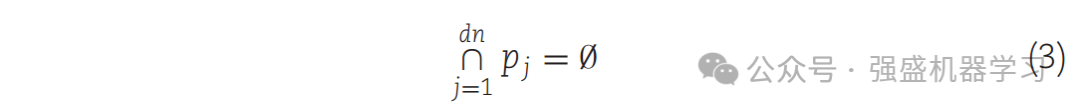
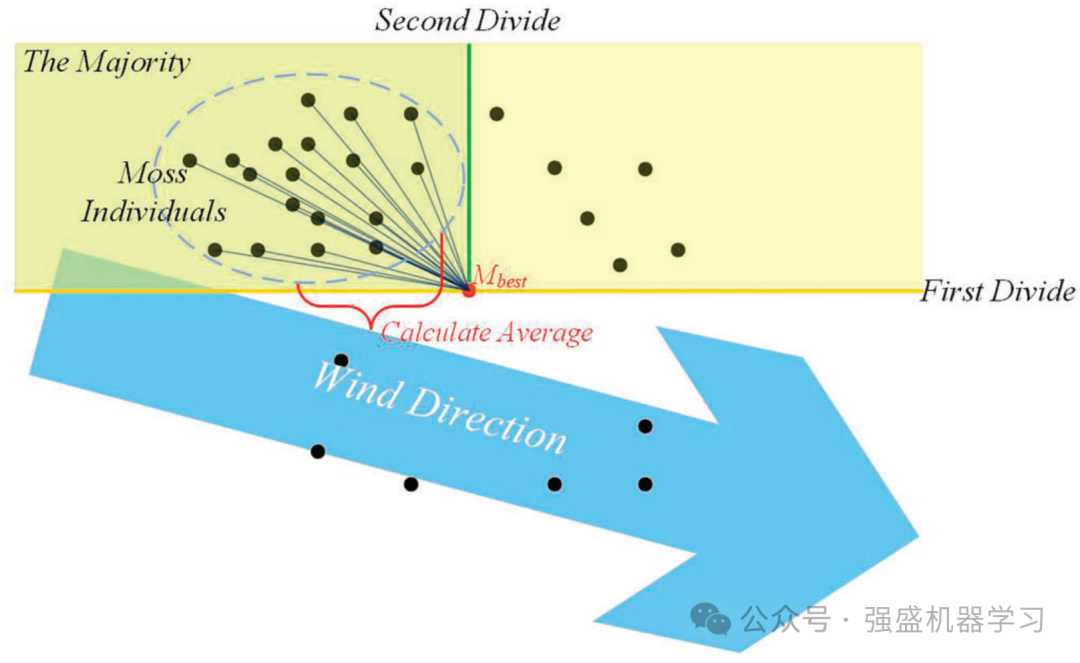
原文作者对风进行了简单的模拟，其中风总是从区域divX到最特殊的个体Mbest，如下图所示。风向的精确计算如式(4)所示：

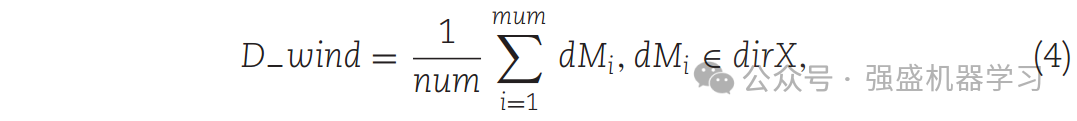
其中D_wind表示计算出的风向，与个体具有相同的维度。变量num表示dirX中的个体总数。dirX的计算可以从式(5)中看出。之所以计算主要个体与Mbest之间的平均距离，是因为这种方法可以平滑个体接近Mbest的路径，从而增强MGO的优化能力。

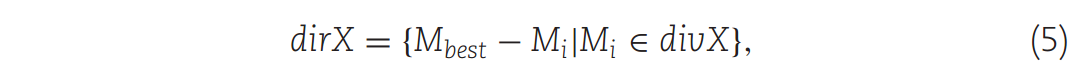
其中dirX表示divX内个体相对于Mbest的距离集合。

二、孢子散布搜索

大多数孢子在稳定的风条件下分散，而一小部分在湍流条件下分散。最终，随着风力减弱，孢子开始在离苔藓更近的地方定居。在本文中，孢子的位置被认为是一种新的解决方案。通过建模模拟孢子在风中的传播特性，如下图所示。孢子的位置由式(6)确定。两步的大小差异显著。这使得个体可以做出随机选择，以防止固定的步长在早期导致缓慢收敛，在后期无法收敛，从而确保种群多样性。

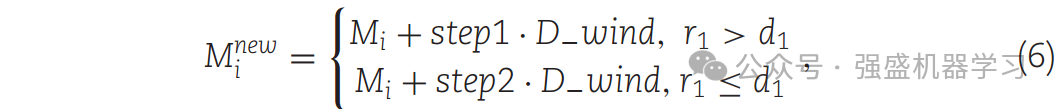
式中，Mnewi表示从i个苔藓个体mi中传播孢子获得的一种新苔藓。r1为（0,1）范围内的随机数，d1为恒定参数，本文将其设为0.2。当r1 > d1时，孢子在稳定的风条件下分散，而在湍流条件下分散。step1为稳定风条件下孢子传播距离，如式(7)所示。step2为湍流风条件下孢子传播距离，如式(8)所示。

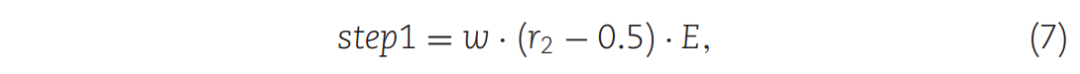
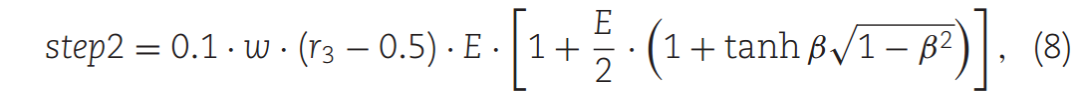
其中w为常数参数，本文设为2。r2是一个在（0,1）范围内的随机向量，其维数与D_wind相同。E为风的强度，其随迭代的进行而减小，如式(9)所示。r3是（0,1）范围内的随机向量，与D_wind具有相同的维数，β的值如式（10）所示。

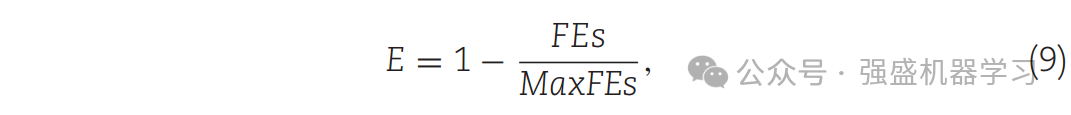
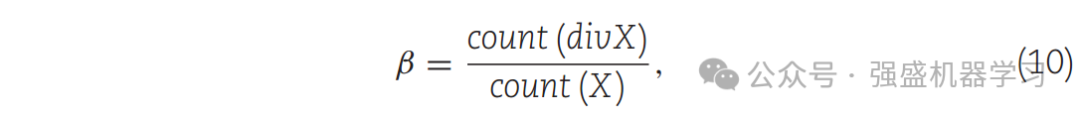
其中FEs表示当前的计算次数，而MaxFEs表示迭代的最大次数，β表示divX中总人数占X中总人数的比例。

三、双传播搜索

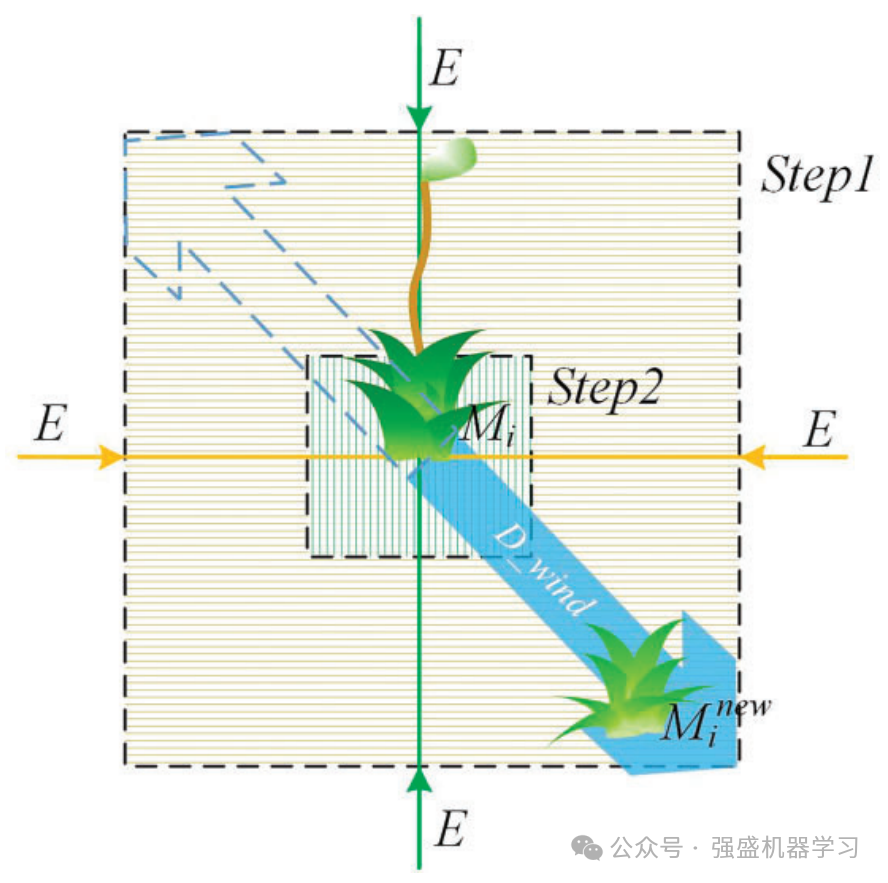
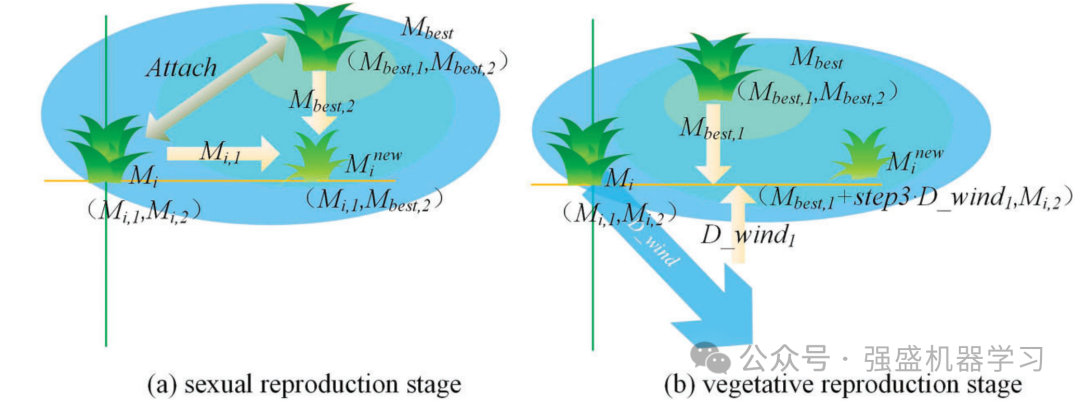
MGO的开发阶段包括双重繁殖搜索，模拟有性繁殖和营养繁殖，通过有性繁殖和营养繁殖产生新的个体，这些个体位于原始个体附近。需要注意的是，在使用双繁殖搜索时，必须满足条件c < 0.8，其中c表示（0,1）范围内的随机数。在有性繁殖过程中，个体基因作为解决方案，允许新个体从当前和最优个体中获取基因。在营养繁殖过程中，苔藓个体的碎片可以发育成新的个体，这被认为是一种新的解决方案。

双传播搜索如下图所示。新苔藓个体的位置由式（11）确定。该方法与传统的MAs不同之处在于，它增加了只改变单个维度的方法的比例，增强了整体的局部勘探能力。

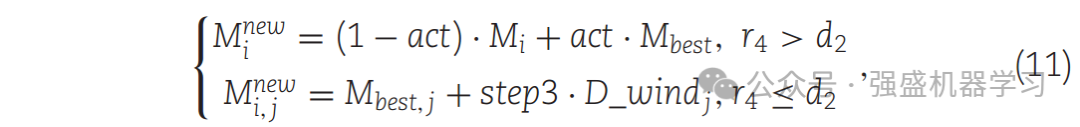
式中，Mnewi表示第i个新个体，Mnewij表示Mnewi中的第j个粒子，j是不超过个体最大维数的随机数。Mbest代表当前最优个体。Mbest中，j表示Mbest中的第j个粒子。D_windj是D_wind中的第j个粒子。R4为（0,1）范围内的随机数，d2为常数参数，本文将其设为0.5。当r4 > d2时，在有性繁殖阶段模拟双繁殖搜索，而在营养繁殖阶段则采用不同的计算方法模拟。然后，评估Mbest内的颗粒是否被利用，如式（12）所示。最后，step3的计算如式（13）所示。

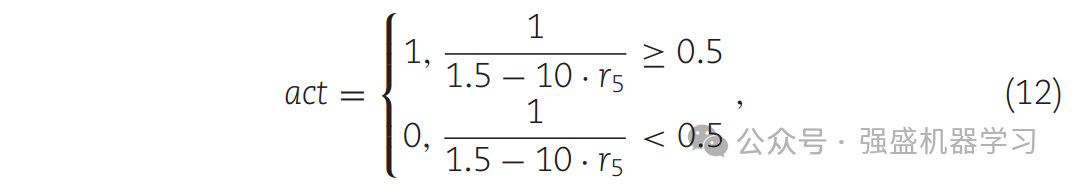
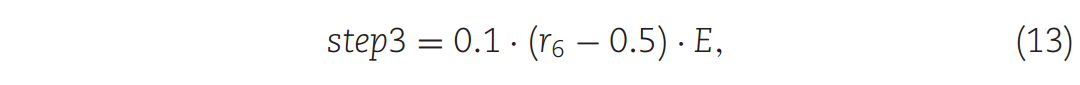
其中r5是（0,1）范围内的随机向量，与Mbest具有相同的维数。r6为（0,1）范围内的随机数，E为风力。

四、隐生机制

隐生现象是指苔藓在一段时间的不活动或干旱后恢复和繁茂的能力。当苔藓面临干旱环境或失去水供应时，它会干燥并进入代谢休眠状态。一旦条件变得有利，苔藓就有能力复苏。

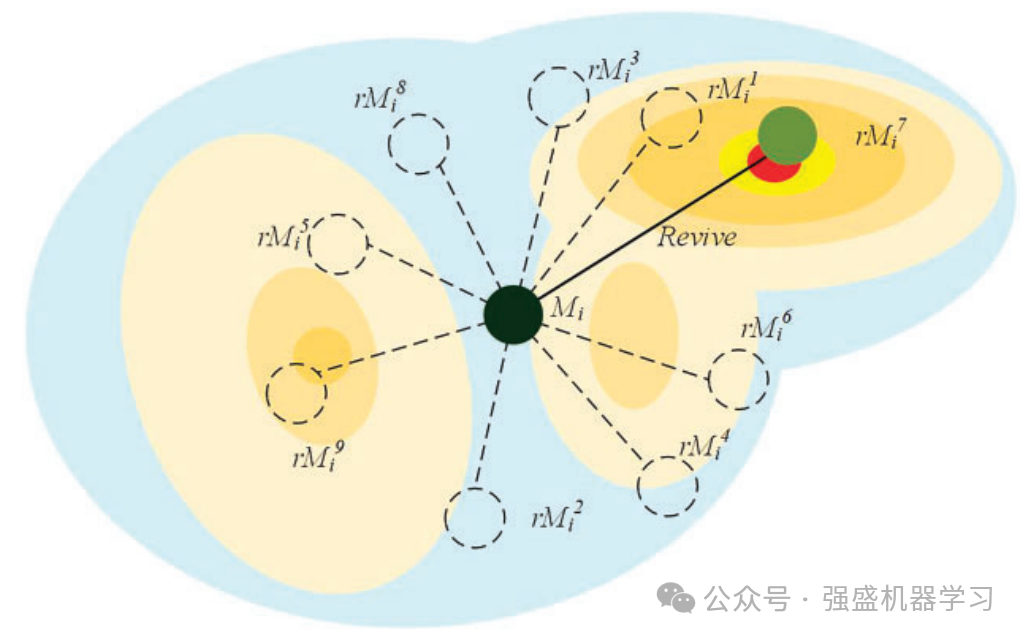
受隐生现象的启发，原文作者提出了一种记录个体历史信息的机制。这种方法不同于直接改变个体的传统方法。相反，这种机制记录每个迭代中产生的个体。一旦满足某些条件，例如达到最大记录数（本文设置为10条）或完成种群迭代，则触发该机制恢复最优个体并替换当前个体。一方面，隐生机制使苔藓个体能够从同一位置重复探索，从而保证了整个种群的全球探索能力。另一方面，个体在一定条件下可以被替代，保证了人口的质量。

隐生机制的一般过程如下图所示。对于苔藓种群中的第i个个体Mi， Mi对应于第0条记录。其余9条记录被标记为rMei，其中e表示Mi的第2条记录。很明显，第7条记录rM7 i获得了最优解。本文将最佳记录标记为rMbesti，然后将Mi修改为rMbesti。

隐生机制的伪代码如Algorithm1所示。

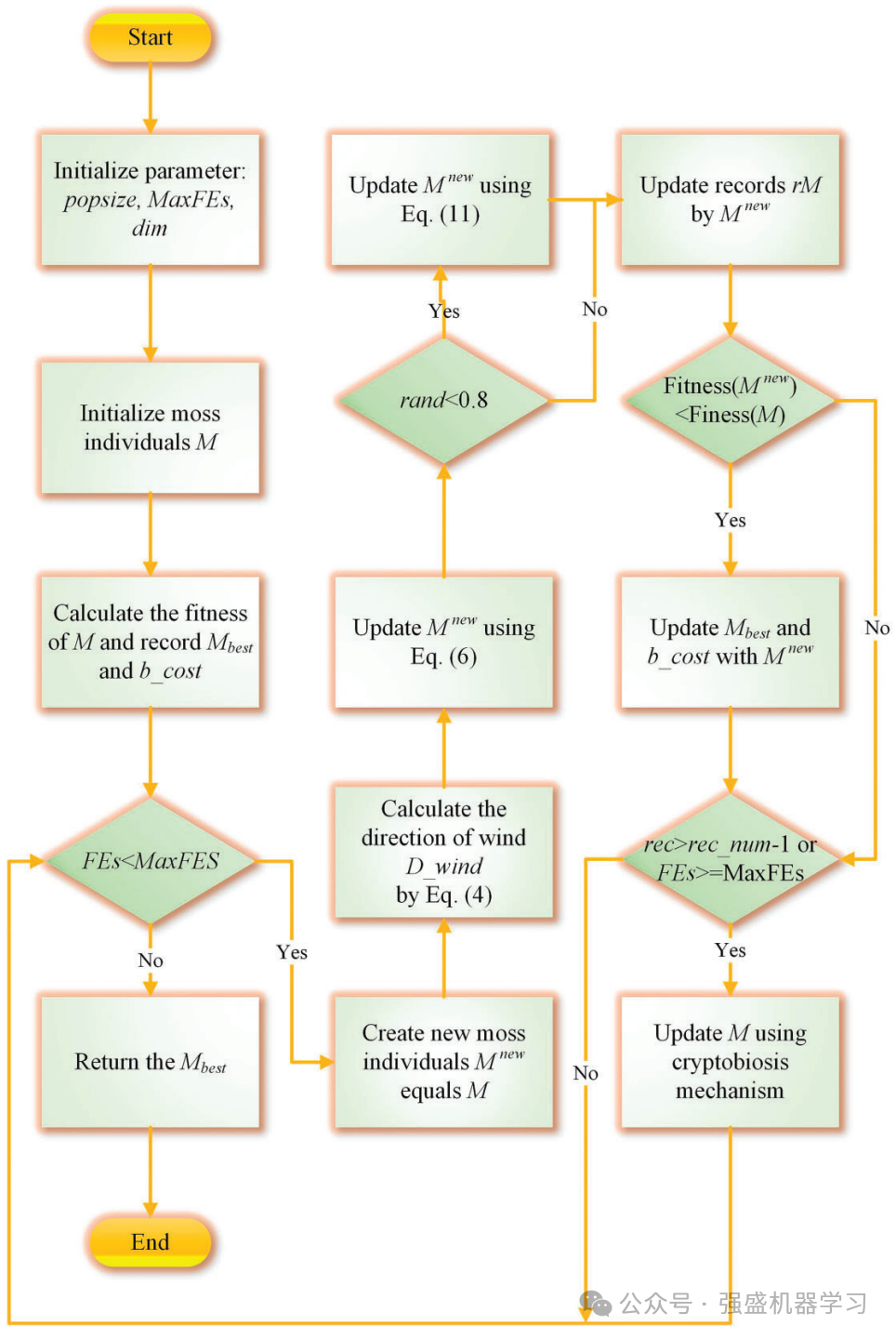
算法流程图和伪代码

为了使大家更好地理解，这边给出作者算法的流程图伪代码，非常清晰！

如果实在看不懂，不用担心，可以看下源代码，再结合上文公式理解就一目了然了！

性能测评

原文作者在CEC 2017和CEC 2022测试函数中，与10种原始和先进的算法进行比较，验证其性能优势，并将MGO应用于四个实际工程问题。实验结果表明其可以有效地解决复杂的工程设计问题。

这边为了方便大家对比与理解，采用23个标准测试函数，即CEC2005，设置种群数量为30，迭代次数为1000，和经典的粒子群优化算法PSO进行对比！这边展示其中5个测试函数的图，其余十几个测试函数大家可以自行切换尝试！

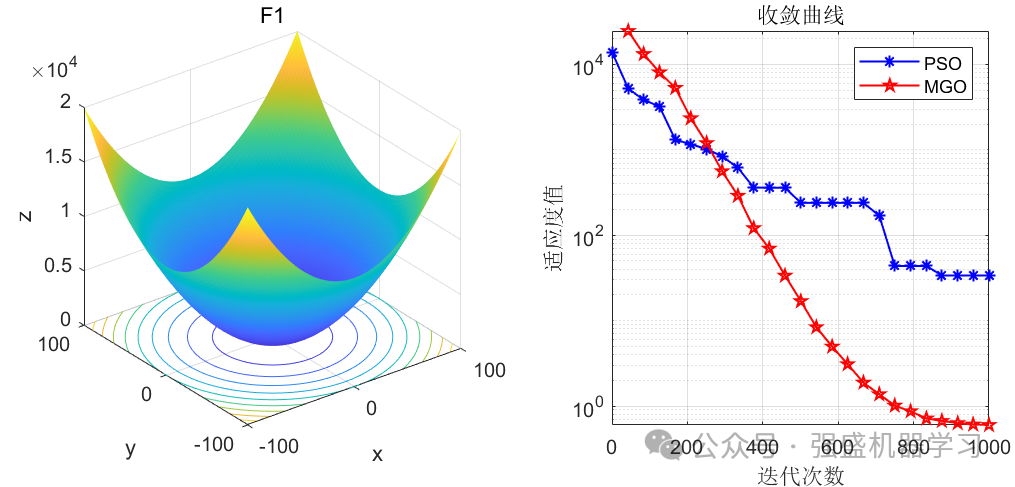
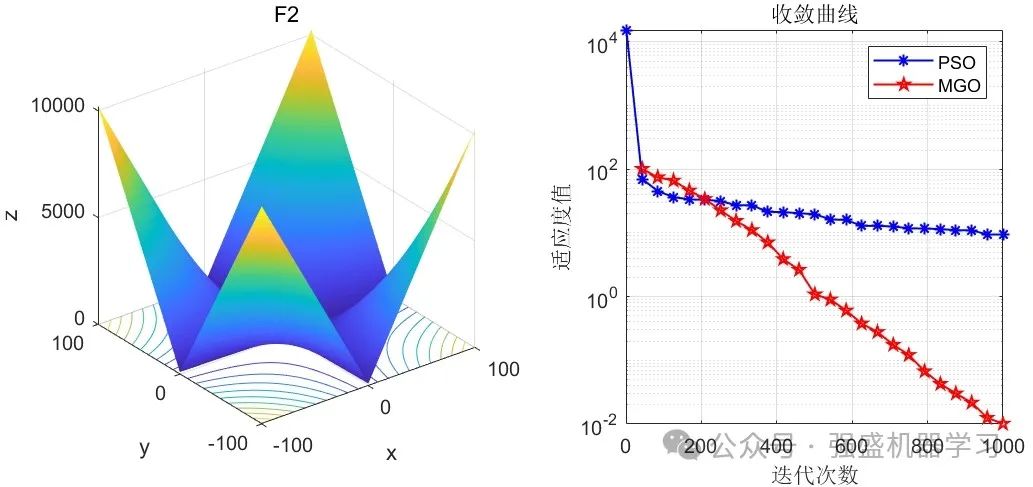
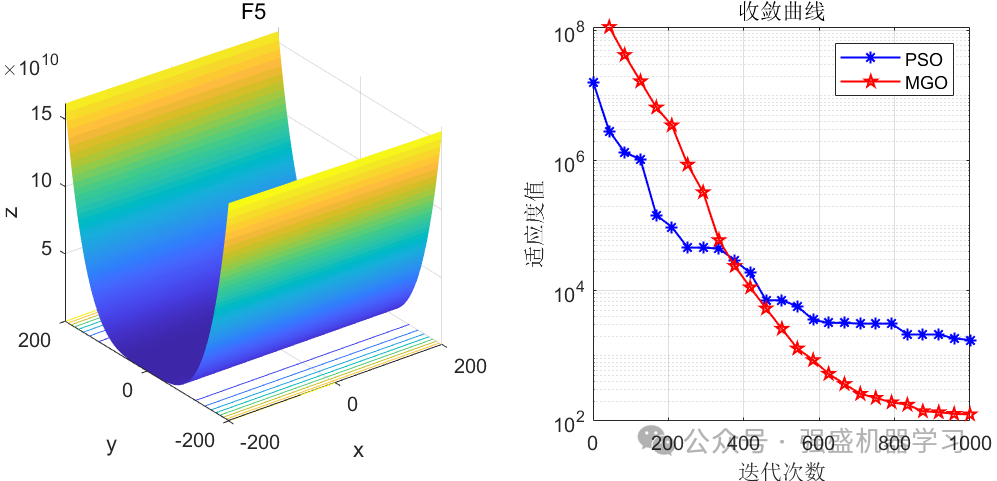
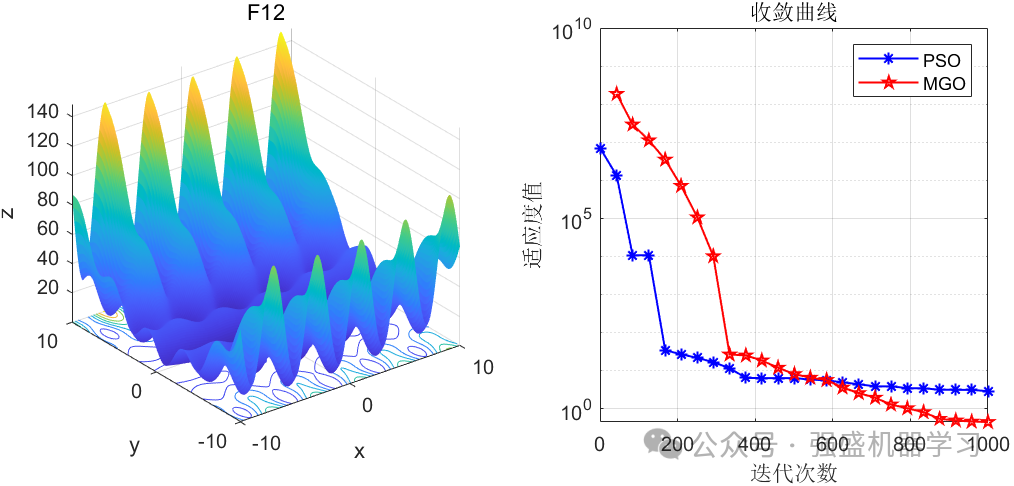
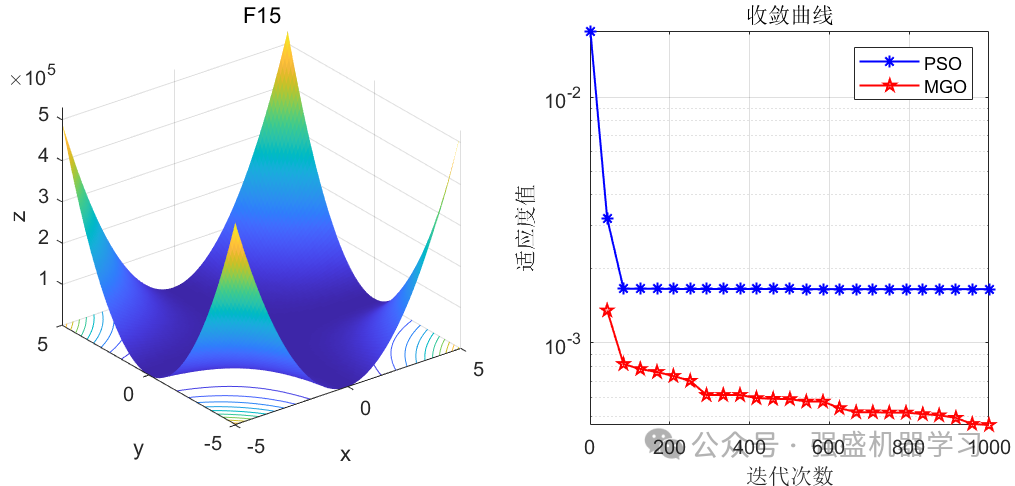
可以看到，这个算法在大部分函数上均优于经典的PSO算法，且拥有不错的跳出局部最优的能力！大家应用到各类预测、优化问题中也是一个不错的选择~

参考文献

[1]Zheng B, Chen Y, Wang C, et al. The moss growth optimization (MGO): concepts and performance[J]. Journal of Computational Design and Engineering, 2024, 11(5): 184-221.

完整代码

如果需要免费获得图中的完整测试代码，只需点击下方小卡片，再后台回复关键字，不区分大小写：

MGO

也可点击下方小卡片，再后台回复个人需求（比如MGO-LSTM）定制以下MGO算法优化模型（看到秒回）：

1.回归/时序/分类预测类：SVM、RVM、LSSVM、ELM、KELM、HKELM、DELM、RELM、DHKELM、RF、SAE、LSTM、BiLSTM、GRU、BiGRU、PNN、CNN、BP、XGBoost、TCN、BiTCN、ESN、Transformer等等均可~

2.组合预测类：CNN/TCN/BiTCN/DBN/Transformer/Adaboost结合SVM、RVM、ELM、LSTM、BiLSTM、GRU、BiGRU、Attention机制类等均可（可任意搭配非常新颖）~

3.分解类：EMD、EEMD、VMD、REMD、FEEMD、TVFEMD、CEEMDAN、ICEEMDAN、SVMD、FMD等分解模型均可~

4.路径规划类：机器人路径规划、无人机三维路径规划、冷链物流路径优化、VRPTW路径优化等等~

5.优化类：光伏电池参数辨识优化、储能容量配置优化、微电网优化、PID参数整定优化、无线传感器覆盖优化、故障诊断等等均可~~

6.原创改进优化算法（适合需要创新的同学）：原创改进2024年的苔藓生长优化算法MGO以及班翠鸟PKO、蜣螂DBO等任意优化算法均可，保证测试函数效果！