【LLM基础教程】从序列切分到上下文窗口02_三种数据切分方法

上一节内容：【LLM基础教程】从序列切分到上下文窗口01_为什么序列建模必须切分数据
本节也是对沐神课程的进一步理解：53 语言模型【动手学深度学习v2】

​ 在上一节中我们看到：序列切分的目的，是把一条很长的文本，转化为模型可以处理的固定长度监督样本。

​ 那么接下来的问题就是：这些长度为$T$的子序列，应该如何从原始文本中取出来？

​ 不同的切分方式，实际上对应着不同的建模假设与工程取舍。在介绍具体策略之前，我们先明确一个统一的训练设定。之后，我们依次介绍三种最常见的策略。

零、统一的训练设定：固定长度的 next-token prediction

​ 为了便于分析，下面所有切分策略都基于同一个基本假设：模型每次处理一段固定长度为$T$的token序列。

1. 输入与输出的构造方式

​ 在语言建模任务中，我们通常采用 next-token prediction 作为训练目标。具体来说：

• 输入：长度为$T$的 token 序列

• 标签：将输入序列整体右移 1 位，长度仍为$T$

• 例如，对于原始 token 序列：
  $$(x_1,x_2,x_3,x_4,x_5,x_6,\cdots )$$
  我们可以构造一个训练样本：

  • 输入：$[x_1,x_2,x_3,x_4,x_5]$
  • 输出：$[x_2,x_3,x_4,x_5,x_6]$

• 这种“输入一段上下文、预测下一步 token”的训练方式，正是语言模型中最经典、也最通用的 next-token prediction 形式。

​ 在这一设定下，序列切分的差异，就体现在：这些长度为$T$的输入片段，是如何从原始长序列中取出的。

(1) 为什么训练形式是「序列 → 序列」

​ 从表面上看，这种训练方式有一个容易让人困惑的地方：输入是一个序列，输出为什么也是一个序列，而不是单个 token？

​ 答案在于：**语言模型的预测目标本身就是“逐时间步定义的”。**也就是说，这并不是人为设计的约定，而是由自回归建模方式自然决定的。

​ 在自回归语言模型中，序列的联合概率通过链式法则分解为：
$$P(x_1,\cdots ,x_T)=\prod _{t=1}^{T}P(x_t|x_{<t})$$
​ 这意味着模型在时间步$t$，模型的目标是预测$P(x_t|x_{<t})$。也就是说，每一个时间步，都对应着一个独立且明确的预测任务。

(2) 一次前向传播，对应$T$次预测

​ 当模型接收一整段长度为$T$的输入序列时，它并不是“等看完再预测”，而是会在内部并行地产生一组预测结果：
$$P(x_{t+1}|x_{\le t}),t=1,2,\cdots ,T$$
​ 从实现角度看：

• 模型会为序列中的 每一个位置 生成一个隐状态

• 每个位置的隐状态，都会输出一个对“下一个 token”的预测分布

  因此，把这$T$个时间步的预测结果一次性组织成一个序列输出，就成为最自然、也是最高效的训练方式。

2. 工程视角下的三点收益

​ 将训练目标设计为“序列 → 序列”，在工程上有非常直接的好处：

• 充分利用监督信号
  一段长度为$T$的真实文本，可以同时提供$T$个预测目标
• 训练与推理形式一致
  训练阶段和自回归生成阶段，遵循同样的“逐 token 预测”逻辑
• 高度并行化
  所有时间步的预测可以在一次前向传播中完成，显著提升训练效率

​ 因此，语言模型“输出也是一个序列”，并不是人为增加的复杂设计，而是由自回归建模方式和模型结构共同决定的自然结果。

一、理论上的滑动窗口（stride = 1）

1. 最直接、也最“完整”的切分方式

• 在所有切分策略中，滑动窗口(sliding window) 是最直观的一种：

  • 窗口长度固定为$T$
  • 每次向前移动 1 个 token（即 stride = 1）
  • 从序列开头一直滑到结尾

• 形式化地说，对于原始序列：$(x_1,x_2,\cdots ,x_N)$，可以构造出如下训练样本：
  $$(x_1,\cdots ,x_T),(x_2,\cdots ,x_{T+1}),\cdots$$
  ​ 对于长度为$N$的原始序列，使用 窗口大小为$T$、步长（stride）为 1 的滑动窗口切分，会得到$N-T$个序列训练样本。

  ​ 此外，可以看到样本高度重叠、数据最密集、信息利用最充分。

2. 为什么它是“理论上的理想方案”

​ 这种方式具有一个非常重要的性质：它最大限度地保留了局部上下文信息。

• 几乎每一个 token，都会出现在多个不同的上下文窗口中

• 模型可以充分学习到条件概率$P(x_t|P_{x<t})$的局部统计规律

  因此，从数据利用率的角度看，滑动窗口通常被视为理论上的理想上界。

• 局限性

  虽然滑动窗口在理论上很优雅，但在工程实践中很少直接使用：

  • 样本数量巨大，计算和存储成本极高
  • 同一 token 会被重复计算多次
  • GPU 并行效率低

  因此，真实训练中通常采用更高效的近似方案。

3. 工程上的现实问题

​ 尽管理论上的滑动窗口（stride = 1）能够完整覆盖所有可能的 next-token 监督信号，但在工程实践中，它会带来一系列非常现实、且难以忽视的问题。

• 相邻样本高度重叠，信息冗余严重

  相邻滑动窗口样本之间，重叠的是$T-1$ 个 token，这意味着新增的计算，往往只引入极少量的“新信息”。模型在连续的多次前向传播中，反复处理几乎相同的上下文。

• 样本数量线性增长，训练规模迅速膨胀

  对于长度为$N$的原始序列，窗口大小为$T$时，滑动窗口（stride = 1）会生成$N-T$个序列级训练样本。

  在大规模语料场景下，$N$往往以百万token计，$N-T\approx N$，这意味着训练样本数几乎与原始语料长度等量增长，数据加载、shuffle、batch 组织的开销显著增加。

• 计算与存储成本难以接受

  将上述两点结合起来，滑动窗口策略会在多个层面放大资源消耗：

  • 计算成本
    大量高度相似的样本，导致重复的前向与反向计算
  • 显存 / 内存压力
    更大的 batch 中包含大量冗余 token，降低有效 token 吞吐率
  • 存储与 I/O 开销
    若提前生成并保存切分后的样本，数据体积会急剧膨胀

  在大模型训练中，这类冗余会直接转化为可观的时间与硬件成本。

• 因此，在实际训练系统中，滑动窗口更多是一种“分析基准”，而不是直接采用的工程方案。

二、随机采样

Random Sampling

1. 为什么需要随机采样

• 在理论上，**滑动窗口（stride=1）**可以生成最完整的训练集；但在工程实践中，它的代价过高：

  • 样本数量随序列长度线性膨胀
  • 相邻样本高度重叠，token 被重复计算
  • 存储、IO 与计算成本都难以接受

  因此，实际系统中更常见的做法是：不构造完整训练集，而是在“潜在完整样本空间”中进行随机采样。

• 随机采样的目标并不是“制造更多样本”，而是：

  • 避免全量滑动窗口带来的资源消耗
  • 在多个 epoch 中不断改变子序列的对齐方式
  • 提升训练过程的随机性与泛化能力

2. 核心思想

​ 与滑动窗口（stride=1）会生成完整训练集不同，随机采样方式并不会生成所有长度为$T$的子序列，而是：

在完整训练集上随机抽取若干子序列用于训练

​ 为此，引入了一个关键设计：随机偏移量 offset：
$$\text{offset}\sim \mathbf{U}(0,T-1)$$

• 这一步的作用是：

  • 随机改变整条序列的“切分起点”
  • 避免模型在每个 epoch 中总是从$x_1$开始看到序列

• 此时，子序列的划分形式变为：
  $$(x_{\text{offset}+1},x_{\text{offset}+2},\cdots ,x_{\text{offset}+T})$$

• 需要特别强调的是：随机采样并不是在子序列内部打乱 token，而是随机选择子序列的起点。

3. 样本之间的关系：不连续、不保证顺序

• 在随机采样中：

  • 每个样本都是从原始长序列中独立截取的一段长度为$T$的子序列
  • batch 内的样本在原始序列中不一定相邻，甚至毫无关系

• 例如，假设这一轮训练随机抽取了 3 个样本，其起点分别为：

  • 样本 A 起点 = 3
  • 样本 B 起点 = 10
  • 样本 C 起点 = 6

  对应的子序列为：
  $$\begin{gathered} A:(x_3,x_4,\cdots ,x_{T+2}) \\ B:(x_{10},x_{11},\cdots ,x_{T+9}) \\ C:(x_6,x_7,\cdots ,x_{T+5}) \end{gathered}$$
  可以看到：

  • A 与 B 在原序列中相距很远
  • C 与 A 有部分重叠，但并非相邻样本
  • batch 内的样本整体呈现为乱序、非连续状态

  这正是随机采样希望达到的效果。

4. 代码实现：基于随机偏移的无重叠子序列采样

​ 下面的实现展示了一个典型的随机采样 DataLoader。在这里，参数batch_size指定了每个小批量中子序列样本的数目， 参数num_steps是每个子序列中预定义的时间步数。

Step 1：随机偏移，避免固定切分边界

offset = random.randint(0, num_steps - 1)
trimmed = corpus[offset:]

​ 这里随机跳过前 offset 个 token，防止模型每一轮训练都看到相同的切分方式。

Step 2：计算可生成的子序列数量（无重叠）

num_subseqs = (len(trimmed) - 1) // num_steps

​ 之所以减 1，是因为语言模型采用 next-token prediction，需要为每个输入 token 提供一个对应的标签。

Step 3：确定所有子序列的起点（等距、不重叠）

initial_positions = list(range(0, num_subseqs * num_steps, num_steps))

​ 每个子序列的起点是等距的(KaTeX parse error: Expected 'EOF', got '_' at position 12: T=\text{num_̲steps})。这些起点为：0, T, 2T, 3T, ...

​ 例如，生成的子序列索引：[0:5], [5:10], [10:15], ...

• 因此生成的子序列满足：

  • 完全不重叠，每个字序列之间相距num_steps
  • 不共享任何 token，每个样本都是从 corpus 中不相交的片段截出来的

  序列:     a b c d e f g h i j k l m n o
  子序列:   └─────┘ └─────┘ └─────┘
              4       4       4
  

Step 4: 打乱子序列起点，实现随机采样

import random
random.shuffle(initial_positions)

​ 随机采样不是按顺序取片段，而是随机选择片段。这样做，保证 batch 内的句子不连续、不相关。

• 例如，原序列：
  $$x_1,x_2,\cdots ,x_{14},x_{15}$$
  设定：

  • num_steps = 5
  • 则可切分的无重叠子序列起点为：

  [0, 5, 10]
  

  • 对应的子序列为：
    • 起点 0 → [x1, x2, x3, x4, x5]
    • 起点 5 → [x6, x7, x8, x9, x10]
    • 起点 10 → [x11, x12, x13, x14, x15]
  • 现在进行随机打乱：[10, 0, 5]
    • Batch1 可能拿的是 [x11, x12, x13, x14, x15]
    • Batch2 可能是 [x1, x2, x3, x4, x5]
    • Batch3 可能是 [x6,x7, x8, x9, x10]

  可以看出，非常随机，不受原始顺序影响。

Step 5: 构造 batch，并生成 X / Y

trimmed corpus
 └── 划分 → num_subseqs = 可切出的所有子序列数量
        └── 按 batch_size 分组
                └── 得到 num_batches 个 batch

num_subseqs = 总子序列数  
batch_size  = 每个 batch 样本数  
num_batches = 总子序列数 / 每个 batch 样本数

• 计算batch个数
  

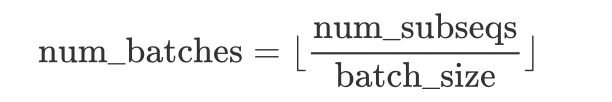
吐槽一下csdn，这里的latex公式无论怎么打都不能正常显示，我是最讨厌用截图来敷衍的。大家将就一下。

• 每个 batch 取 batch_size 个起点，每个起点对应一个长度为 num_steps 的子序列

  for i in range(0, batch_size * num_batches, batch_size):
      batch_positions = initial_positions[i:i + batch_size]
  

  这里的batch_positions是从initial_positions中取出的一个 batch 里的起始位置集合。

  • 例如：

    initial_indices = [200, 40, 600, 20, 480, 300, ...]  # 已打乱
    
    batch_size = 2
    第一次 batch -> [200, 40]
    第二次 batch -> [600, 20]
    ...
    

• 构造输入序列 X 与标签序列 Y

  def get_subseq(start):
      return trimmed[start:start + num_steps]
  
  X = [get_subseq(pos) for pos in batch_positions]
  Y = [get_subseq(pos + 1) for pos in batch_positions]
  

完整实现：

import random
import torch

def seq_data_iter_random(corpus, batch_size, num_steps):
    """
    随机采样方式的小批量序列生成器
    corpus: 整个语料（token 序列）
    batch_size: 每个 batch 中的样本数量
    num_steps: 每个子序列的长度
    """
    # ---- 1. 随机偏移 ----
    offset = random.randint(0, num_steps - 1)
    trimmed = corpus[offset:]

    # ---- 2. 计算可切分的子序列数量 ----
    num_subseqs = (len(trimmed) - 1) // num_steps
    initial_positions = list(range(0, num_subseqs * num_steps, num_steps))

    # ---- 3. 打乱所有子序列的起点 ----
    random.shuffle(initial_positions)

    def get_subseq(start):
        return trimmed[start:start + num_steps]

    # ---- 4. 构造 batch ----
    num_batches = num_subseqs // batch_size
    for i in range(0, batch_size * num_batches, batch_size):
        batch_positions = initial_positions[i:i + batch_size]

        X = [get_subseq(pos) for pos in batch_positions]
        Y = [get_subseq(pos + 1) for pos in batch_positions]

        yield torch.tensor(X), torch.tensor(Y)

• 例如，我们生成一个从$0$到$34$的序列。 假设批量大小为$2$(batch_size=2)，时间步数为$5$(num_steps=5)，这意味着可以生成$\lfloor \frac{35-1}{5}=6\rfloor$个“特征－标签”子序列对。 因为每个小批量中的样本为2，我们只能得到3个小批量。

  my_seq = list(range(35))
  batch_count = 0
  for X, Y in seq_data_iter_random(my_seq, batch_size=2, num_steps=5):
      print(f"=====batch {batch_count+1}======")
      print('X: ', X, '\nY:', Y)
      batch_count += 1
  

  =====batch 1======
  X:  tensor([[15, 16, 17, 18, 19],
  [ 0,  1,  2,  3,  4]]) 
  Y: tensor([[16, 17, 18, 19, 20],
  [ 1,  2,  3,  4,  5]])
  =====batch 2======
  X:  tensor([[20, 21, 22, 23, 24],
  [25, 26, 27, 28, 29]]) 
  Y: tensor([[21, 22, 23, 24, 25],
  [26, 27, 28, 29, 30]])
  =====batch 3======
  X:  tensor([[ 5,  6,  7,  8,  9],
  [10, 11, 12, 13, 14]]) 
  Y: tensor([[ 6,  7,  8,  9, 10],
  [11, 12, 13, 14, 15]])
  

  

5. 为什么随机采样要这样设计

​ 从建模假设上看，随机采样并不要求不同子序列之间保持原始文本中的连续性。这是因为，在语言模型的训练目标中，每一个长度为$T$的子序列，本身就已经构成了一个完整、独立的监督样本。

​ 具体来说，语言模型采用的是 next-token prediction 训练形式：

X = [t0, t1, t2, t3, t4]
Y = [t1, t2, t3, t4, t5]

​ 在这一设定下，模型在每一个时间步$t$，只关心：$P(t_{i+1}\mid t_{\le i})$，监督信号完全来自子序列内部，不依赖于相邻子序列是否在原始语料中连续。

​ 因此，从训练目标的角度看：只要子序列内部保持 token 的顺序关系，不同子序列之间是否相邻，并不会影响 next-token prediction 的正确性。

• 在这一前提下，随机采样的设计带来了非常明确的工程优势：

  • 高度并行化
    每个子序列都是独立样本，可以在 GPU 上同时计算，不需要维护跨序列状态。
  • 便于打乱与随机化
    通过打乱子序列起点，可以有效减弱位置偏置（position bias），使模型不会过度依赖特定位置模式。
  • 计算与存储效率更高
    子序列之间不重叠，避免了同一个 token 在大量样本中被重复计算，从而显著降低计算成本。

• 从这个角度看，“不重叠”并不是信息利用不足，而是一种有意识的工程取舍：在不改变训练目标的前提下，用更少的重复计算，获得足够多、足够随机的监督信号。

  这也是为什么，在实际的语言模型训练系统中，随机采样往往比 stride=1 的滑动窗口更常用。

三、顺序采样

Sequential Sampling

​ 在语言模型（尤其是 RNN / LSTM / 早期 Transformer）中，序列的连续性本身就是一种重要信号：

• 句法结构是跨 token 延续的

• 语义状态会随时间逐步演化

• 隐状态（hidden state）天然假设时间连续

  因此，与完全打乱的随机采样不同，顺序采样试图最大程度保留原始语料的时间结构。

1. 顺序采样的动机

​ 随机采样强调样本独立性和并行效率，但它刻意破坏了时间上的连续性。而在某些场景（尤其是 RNN / LSTM）中，我们希望：**模型在 batch 内仍然能够看到连续的上下文片段。**顺序采样正是为此而设计的。

• 核心思想：让模型看到语料中“连续”的序列片段，尽可能保持上下文的自然衔接。

• 顺序采样的特点可以概括为：

  • 不打乱语料的整体顺序
  • batch 内的每一行是一段连续时间序列
  • 行与行之间相互独立

  其本质是：在保持 batch 并行计算的前提下，尽量保留时间维度上的连续性。

2. 与随机采样的根本区别

• 随机采样： 把语料视为一个“token 池”，子序列之间不要求相关性

• 顺序采样： 把语料视为一条“长时间序列”，子序列是这条序列的切片

• 与随机采样不同，顺序采样中整个 corpus 会被按顺序切成若干子片段。
  

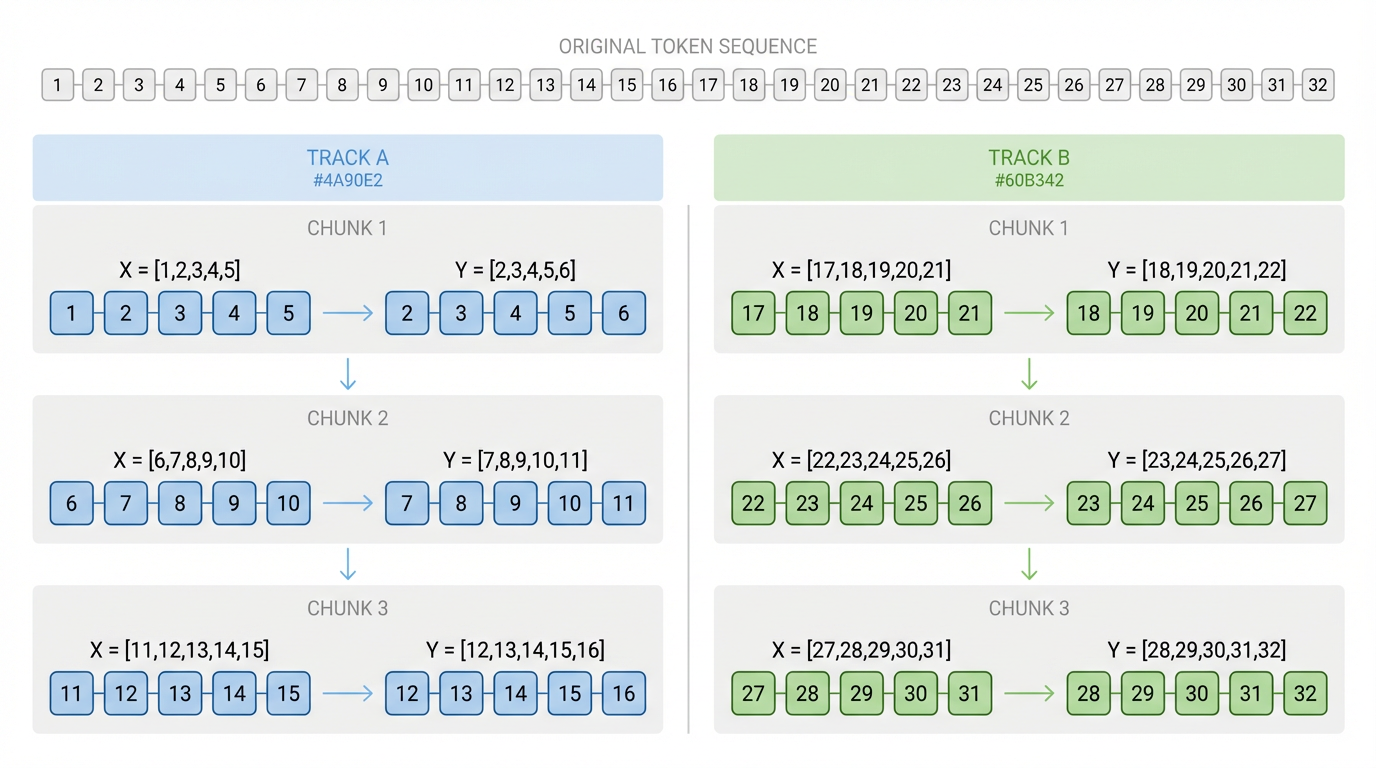
  这也是为什么顺序采样更常用于：

• RNN / LSTM 的语言模型

• 需要跨 batch 传递隐状态的训练方式

• 分析模型对长期依赖的建模能力

3. 顺序采样的实现

Step 1：随机偏移（Random Offset）

# ---- 1. 随机偏移 ----
offset = random.randint(0, num_steps)

• 为什么需要 offset？

  如果每个 epoch 都从 corpus[0] 开始切分，那么：

  • 每一轮训练看到的子序列切分位置完全相同
  • 模型容易记住“切分边界”，而不是语言规律
  • 泛化能力会明显下降

• 随机偏移的作用是：

  • 打破固定切分边界
  • 让同一个 token 在不同 epoch 中出现在不同位置
  • 在不破坏顺序结构的前提下引入随机性

• 在顺序采样中，offset 可以取到 num_steps（闭区间），因为我们后面是 先构造大段序列，再 reshape，不会产生越界问题。

Step2：计算可用于 batch 的 token 数

num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size

​ 这一行是纯工程约束，但非常关键。

• len(corpus) - offset - 1：可用的 token 数，其中- offset是跳过随机起点之前的 token；

  - 1：为构造 Y（右移一位）预留空间

• // batch_size：按 batch_size 整除，避免最后出现“凑不齐一个 batch” 的情况

• * batch_size：重新计算出可整除的 token 数

  顺序采样的一个重要特点是：我们宁愿丢掉少量尾部数据，也要保证 batch 内结构严格一致。

Step3：构造 X 和 Y（严格对齐的 next-token prediction）

Xs = torch.tensor(corpus[offset : offset + num_tokens])
Ys = torch.tensor(corpus[offset + 1 : offset + 1 + num_tokens])

​ 这是语言模型中最经典、也是最“干净”的训练格式：

• X（输入）：

  [t0, t1, t2, ..., tn-1]
  

• Y（标签）：

  [t1, t2, t3, ..., tn]
  

  二者长度完全一致，只是整体右移一位。这正是 next-token prediction 的数学实现形式：$P(x_{t+1}\mid x_{\le t})$。

Step 4：reshape 成 batch_size 行的“并行长序列”

Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)

​ 此时，每一行是一条 时间上连续的长序列，不同行之间是 相互独立、并行训练的样本

​ 可以把它理解为：我们从一条超长时间轴中， “抽取了 batch_size 条并行时间轨道”

Step 5：按 num_steps 切出连续的训练片段

num_batches = Xs.shape[1] // num_steps

for i in range(0, num_steps * num_batches, num_steps):
    X = Xs[:, i: i + num_steps]
    Y = Ys[:, i: i + num_steps]
    yield X, Y

这里切出来的每一个 (X, Y)：

• 在行内是连续的 token
• 在列方向保持严格对齐
• 在 batch 之间 时间顺序不被打乱

这一步确保了：模型在训练时，看到的是“自然语言原本的时间展开方式”。

完整实现

def seq_data_iter_sequential(corpus, batch_size, num_steps):  #@save
    """使用顺序分区生成一个小批量子序列"""
    # 从随机偏移量开始划分序列
    offset = random.randint(0, num_steps)
    num_tokens = ((len(corpus) - offset - 1) // batch_size) * batch_size
    Xs = torch.tensor(corpus[offset: offset + num_tokens])
    Ys = torch.tensor(corpus[offset + 1: offset + 1 + num_tokens])
    Xs, Ys = Xs.reshape(batch_size, -1), Ys.reshape(batch_size, -1)
    num_batches = Xs.shape[1] // num_steps
    for i in range(0, num_steps * num_batches, num_steps):
        X = Xs[:, i: i + num_steps]
        Y = Ys[:, i: i + num_steps]
        yield X, Y
        
        
my_seq = list(range(35))
for X, Y in seq_data_iter_sequential(my_seq, batch_size=2, num_steps=5):
		print('X: ', X, '\nY:', Y)

输出：

X:  tensor([[ 1,  2,  3,  4,  5],
     [17, 18, 19, 20, 21]]) 
Y: tensor([[ 2,  3,  4,  5,  6],
     [18, 19, 20, 21, 22]])
X:  tensor([[ 6,  7,  8,  9, 10],
     [22, 23, 24, 25, 26]]) 
Y: tensor([[ 7,  8,  9, 10, 11],
     [23, 24, 25, 26, 27]])
X:  tensor([[11, 12, 13, 14, 15],
     [27, 28, 29, 30, 31]]) 
Y: tensor([[12, 13, 14, 15, 16],
     [28, 29, 30, 31, 32]])

​ 输出示例清楚地说明：

• 每一行内部是严格连续的 token

• 不同行是并行的独立样本

• batch 之间保持时间顺序推进：同一行在不同 batch 中是连续的。

  这正是顺序采样的设计目标：时间连续性不是体现在 batch 内，而是体现在 batch 之间

四、三种切分方式的对比与取舍

​ 在理论上，如果对一个长度为$n$的序列进行建模，最“彻底”的方式是采用 滑动窗口（stride = 1），在每一个时间步都构造一个训练样本。

​ 但在实际训练系统中，无论是随机采样还是顺序采样，生成的$X$样本通常都是互不重叠的，而不是每个时间步都生成一个样本。

​ 这是一个工程取舍问题，而不是建模正确性的问题。

1. 整体对比

方式	是否重叠	样本数量	计算效率	使用场景
滑动窗口	是	极多	低	小数据、分析验证
随机采样	否	适中	高	大规模训练
顺序采样	否	适中	高	保留上下文

重叠样本不是“更正确”，而是一种成本极高的策略。

​ 在大规模训练中，不重叠 + 批量并行，往往性价比更高。

1. 理论滑动窗口 VS 实际训练切分

​ 以序列长度为$n$，num_steps=5 为例：

方式	样本长度	样本数量	是否重叠	优缺点
理论滑动窗口	5	$n-5+1$	是	最大化训练样本数量，但训练效率低
常规 seq / random	5	$\lfloor n/5\rfloor$	否	高效、课并行、上下文连续、训练稳定

​ 可以看到，两者的本质差异并不在于样本形式，而在于是否允许重叠。

2. 滑动窗口采样的样本数量是如何膨胀的

​ 假设序列长度为$n$：
$$x_0,x_1,\cdots ,x_{n-1}$$
​ 我们希望 每个样本长度为num_steps，并用于预测下一个 token（或下一个 num_steps 个 token）：

• 滑动窗口方式（步长 = 1）：

  • 每个样本长度 = num_steps
  • 样本 KaTeX parse error: Expected 'EOF', got '_' at position 42: … x_{i+\text{num_̲steps}-1}]
  • 对应的KaTeX parse error: Expected 'EOF', got '_' at position 46: … x_{i+\text{num_̲steps}}]

• 如果 num_steps = 5，那么第一条样本i=0就是：
  $$\begin{gathered} X[0]=[x_0,x_1,\cdots ,x_4] \\ Y[0]=[x_1,x_2,\cdots ,x_5] \end{gathered}$$

  • 第二条样本（滑动一步）：
    $$\begin{gathered} X[1]=[x_1,x_2,\cdots ,x_5] \\ Y[1]=[x_2,x_3,\cdots ,x_6] \end{gathered}$$

  • …依此类推，最终可生成的样本数量为： n - num_steps

• 但是：相邻样本之间共享 num_steps − 1 个 token，高度重叠。

3. 为什么实际 batch 训练中不构造$n-1$个样本

• 在真实训练中，我们通常不会采用 stride = 1 的滑动窗口，而是：

  • 一次取 num_steps 个时间步作为一个样本
  • 在 batch 维度上并行训练多条序列轨道

• 具体来说：

  • 若序列长度为$n$
  • 每个样本长度为 num_steps
  • 最多可以生成 KaTeX parse error: Expected 'EOF', got '_' at position 22: …r n / \text{num_̲steps} \rfloor 个 互不重叠的样本。

• 这样做的好处：

  • 避免重复计算

    • 滑动窗口会反复计算几乎相同的 token 组合

  • 显著提升 GPU 利用率

    • 不重叠样本更适合批量并行

  • 训练更稳定

    • 减少高度相关样本带来的梯度冗余

  • 更贴合现代模型训练范式

    • Transformer / GPT 并不依赖跨样本隐状态

⚠️ 如果希望引入更多上下文覆盖，可以使用 步长 < num_steps 的滑动窗口，但这一定会带来更高的时间与显存成本。