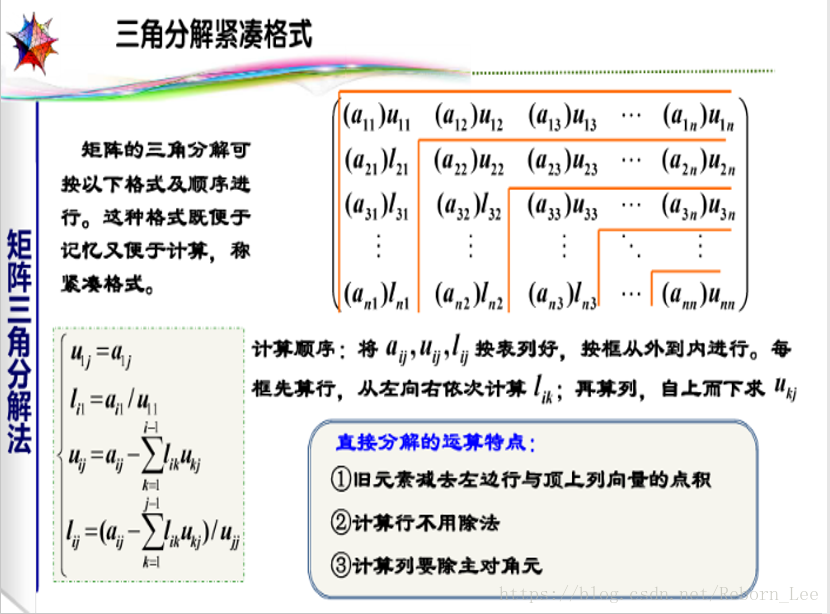
上篇博文由高斯消去法的矩阵形式推出了矩阵的LU分解:矩阵的三角分解法;
实际上,可以直接处理矩阵,得到矩阵的LU分解,这就是矩阵的直接LU分解;直接通过矩阵的元素得到计算LU元素的递推公式,不需要任何中间步骤。
学过矩阵论的都知道矩阵的LU直接分解法,数值分析这里又来了一遍,说明很重要了,事实上,这部分内容真的一点都不难,记得当初大家一起复习矩阵论时候,对这块内容,大家的分解方法各种各样,都认为自己的方法最好最简单,哈哈,这是好事,但最终的结果是一考完试就全部忘了,还管什么最简便方法,所以最后最吃香的还是正正规规地解法,过了一段时间还能捡起来用的主流方法。
下面直接上图:
Doolittle直接分解法:




看到这里,好像对简便运算没什么卵用,紧凑格式只是列举了计算好的L和U放到一起,我要这(紧凑格式)(铁棒)有何用?
继续看:
按下图的说法,这种紧凑格式貌似有用,可是计算机变成如何实现呢?(遇到实际问题再说吧,这里仅仅为了考试记忆。)
联系LU分解:
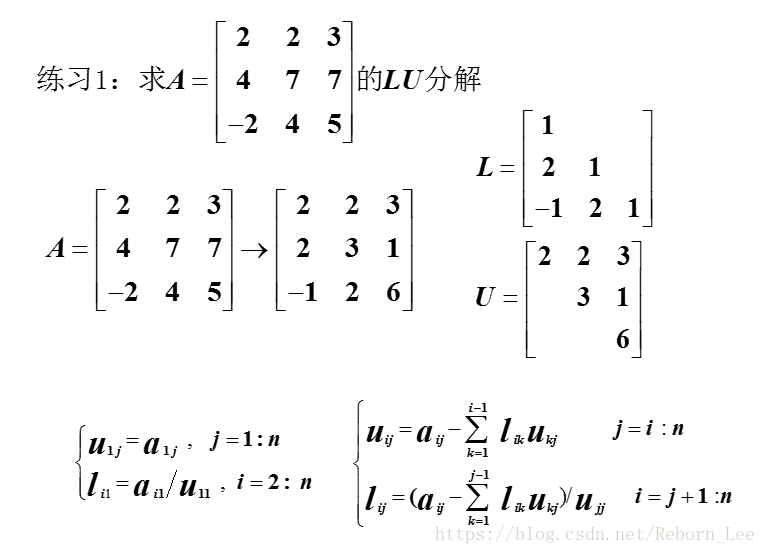
再举一个例子,维度大一些更能体会这些计算过程:

————————————————————————————————————————————————————
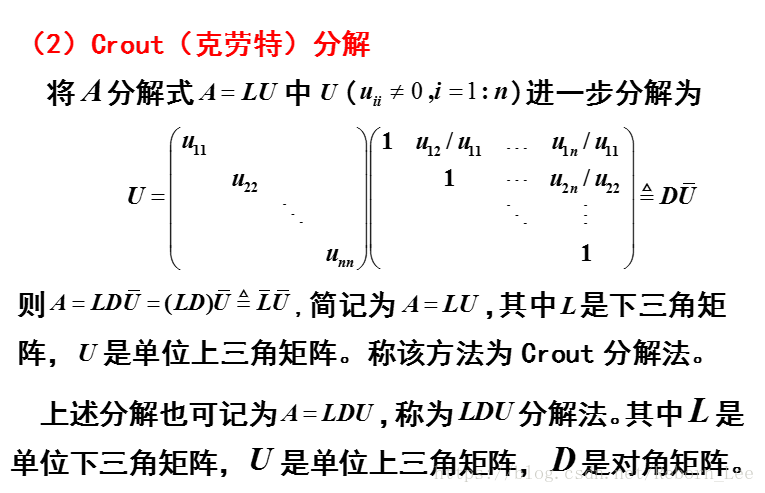
Crout分解:
Doolittle分解将矩阵分解成一个单位下三角矩阵和一个上三角矩阵,而Crout分解是将矩阵分解为一个下三角分解和一个单位上三角矩阵;
所以套路是一样的,你说是不是dan teng;如果我只记忆一种分解,那公式我也能记住,可是又多了这一个,这样dt之处在于这样会让人突然混乱哪一个是Doolittle分解,哪一个是Crout分解;
如果你不考试,就不要看了,都是一样的东西,又说了一遍。
如果A是对称矩阵,也可以当成普通的矩阵处理,处理完了之后就有下面的东西了,当做茶余饭后吧,狗头上戴个帽子的事情。


Crout分解就说这么多,哈哈,可见被代替了。
————————————————————————————————————————————————————
实对称正定矩阵的平方根分解:

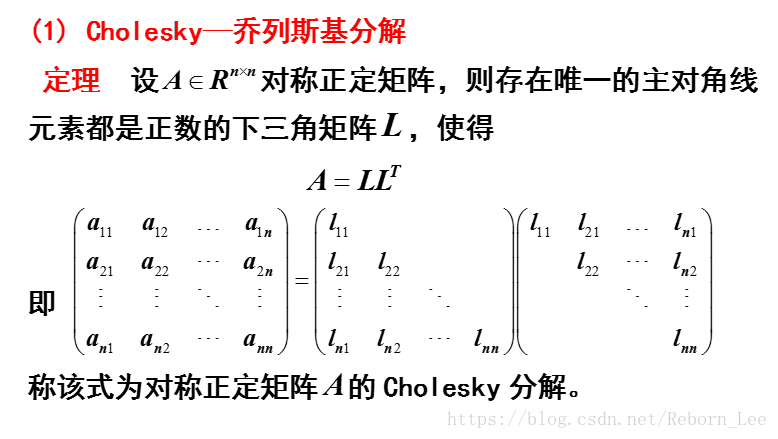
记住这个矩阵分解式就可以了。



针对缺点提出改进的平方根法,不得不说人类的智慧让人佩服:

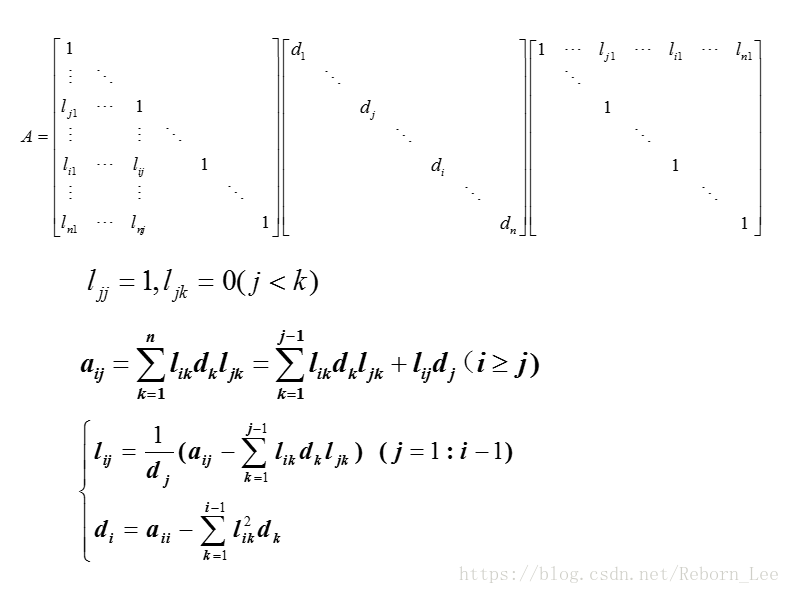
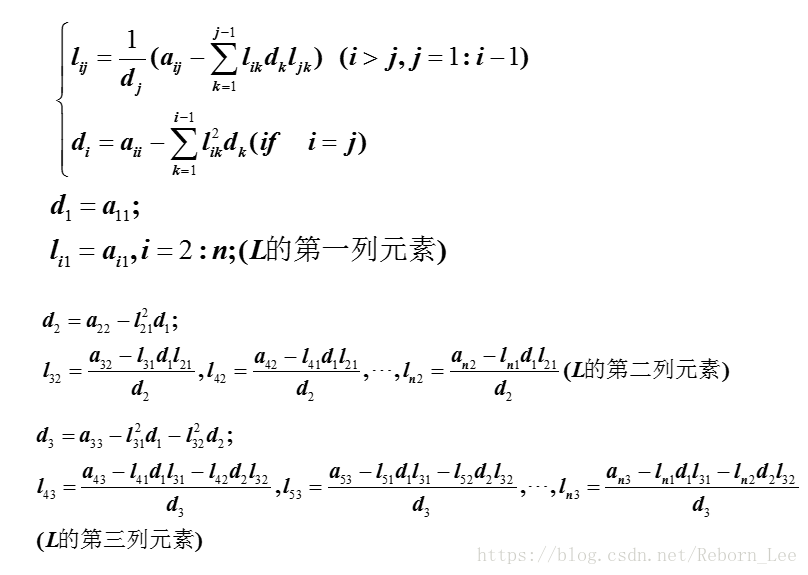
看看就行,这公式我都不理会。
直接举例:
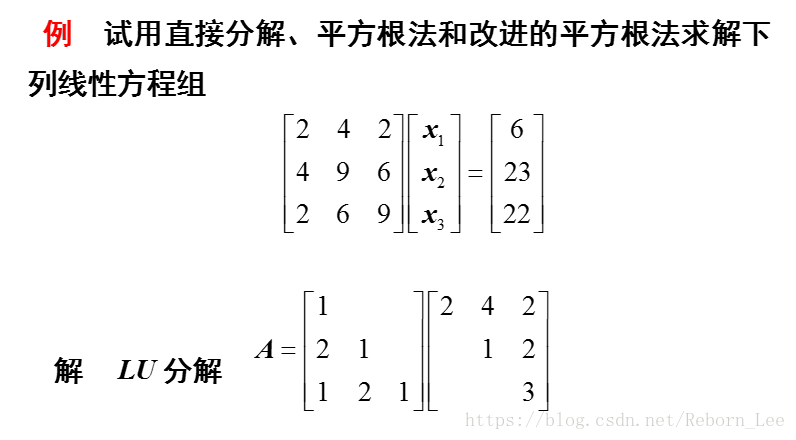























 4641
4641

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










