机器学习 | 机器学习之巅SVM系列(一)
本文记录了SVM的前提知识,即拉格朗日对偶问题
文章目录
一、优化函数的原始问题
假设 f ( x ) f(x) f(x), c i ( x ) c_i(x) ci(x), h i ( x ) h_i(x) hi(x)是定义在 R n R^n Rn上的连续可微函数(为什么要求连续可微呢,后面再说,这里不用多想)。
无约束条件,可行解区域外
若不考虑约束条件,即可行解区域外,则原始优化问题仅仅为:
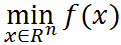
由于设
f
(
x
)
f(x)
f(x)连续可微,利用高中的知识,对
f
(
x
)
f(x)
f(x)求导数,然后令导数为0,就可解出最优解。
考虑约束条件,可行解区域内
若考虑约束最优化问题,原始问题将转为:
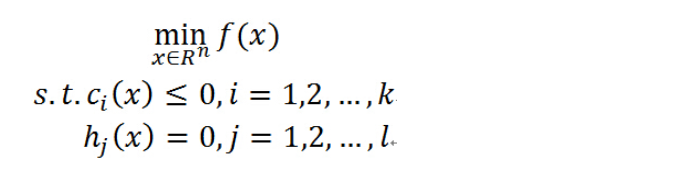
由于增加了约束条件,则不能直接对
f
′
(
x
)
=
0
f'(x)=0
f′(x)=0求解,因为需要满足约束条件,这就非常的狗血。那么能否将约束条件化解掉???
拉格朗日函数就是干这个的!
二、引入拉格朗日函数
前言:引入拉格朗日函数,目的是将有约束问题转化为无约束问题
广义的拉格朗日函数如下所示:
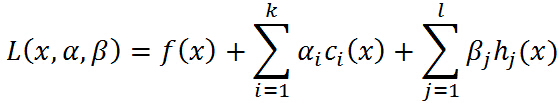
其中, 特别要求
α
i
≥
0
\alpha_i \ge0
αi≥0
现在,如果把
L
(
x
,
α
,
β
)
L(x, \alpha, \beta)
L(x,α,β)看作是关于
α
,
β
\alpha, \beta
α,β的函数,其最大值为:

因此
L
(
x
,
α
,
β
)
L(x, \alpha, \beta)
L(x,α,β)在求得了
α
,
β
\alpha, \beta
α,β最大值后,
m
a
x
α
,
β
:
α
i
≥
0
L
(
x
,
α
,
β
)
\mathop{max}\limits_{\alpha, \beta:\alpha_i\ge0}L(x,\alpha,\beta)
α,β:αi≥0maxL(x,α,β)仅是一个关于x的函数。
定义这个函数为
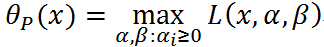
下面通过 x x x是否满足约束条件两方面来分析这个函数:
-
考虑 x x x违反了原始问题的约束,即 c i ( x ) > 0 c_i(x)>0 ci(x)>0或者 h j ( x ) ≠ 0 h_j(x)\neq0 hj(x)=0, 则
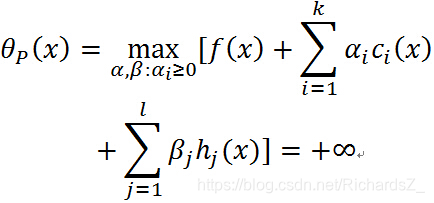
当 α i \alpha_i αi-> + ∞ +\infty +∞, h j ( x ) ≠ 0 h_j(x)\neq0 hj(x)=0,则很容易取值 β j \beta_j βj使得 β j h j ( x ) \beta_jh_j(x) βjhj(x)-> + ∞ +\infty +∞, 因此
θ p ( x ) = m a x α , β : α i ≥ 0 [ f ( x ) + ∑ i = 1 k α i c i ( x ) + ∑ j = 1 l β j h j ( x ) ) ] \theta_p(x)=\mathop{max}\limits_{\alpha, \beta:\alpha_i\ge0}[f(x)+\sum\limits_{i=1}^k\alpha_ic_i(x)+\sum\limits_{j=1}^l\beta_jh_j(x))] θp(x)=α,β:αi≥0max[f(x)+i=1∑kαici(x)+j=1∑lβjhj(x))] -> + ∞ +\infty +∞ -
考虑 x x x满足原始问题的约束,即可行解区域内,原优化问题的约束条件都得到满足,
-
因为 h j ( x ) = 0 h_j(x)=0 hj(x)=0,所以不论 β \beta β怎么取值,必然有 β h j ( x ) = 0 \beta h_j(x)=0 βhj(x)=0,
-
因为 c i ( x ) < 0 c_i(x)<0 ci(x)<0,且限定了 α i ≥ 0 \alpha_i\ge0 αi≥0,因此 α i c i ( x ) \alpha_i c_i(x) αici(x)最大值为0
综上所述, 原始优化问题根据约束可分为两种结果

那么在满足约束条件下,求解f(x)在可行解区域内的最小化,等于:
m
i
n
x
θ
p
(
x
)
=
m
i
n
x
[
m
a
x
α
,
β
:
α
i
≥
0
L
(
x
,
α
,
β
)
]
=
m
i
n
x
f
(
x
)
\mathop{min}\limits_x\theta_p(x)=\mathop{min}\limits_{x}[\mathop{max}\limits_{\alpha, \beta:\alpha_i\ge0}L(x,\alpha,\beta)] = \mathop{min}\limits_{x}f(x)
xminθp(x)=xmin[α,β:αi≥0maxL(x,α,β)]=xminf(x)
这下可以看出,
m
i
n
x
θ
p
(
x
)
\mathop{min}\limits_x\theta_p(x)
xminθp(x)等价于原始优化问题,下标P表示原始问题,
定义原始问题最优解
p
∗
=
m
i
n
x
θ
p
(
x
)
p^*=\mathop{min}\limits_x\theta_p(x)
p∗=xminθp(x)
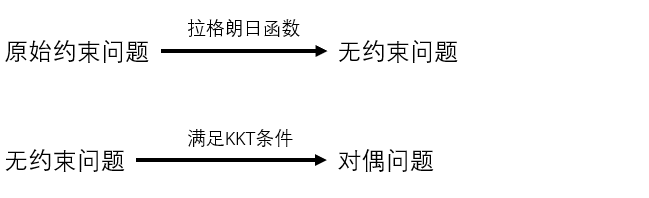
小结:通过拉格朗日函数可将原始带有约束的有话题转化为无约束的优化问题!
三、对偶问题
什么是对偶问题
前言:在原始优化问题求解困难时,若问题满足KKT条件,可将原始问题转为其对偶问题进行求解
定义对偶优化问题,是关于 α , β \alpha, \beta α,β的函数:
θ D ( α , β ) = m i n x L ( x , α , β ) \theta_D(\alpha,\beta)=\mathop{min}\limits_{x}L(x,\alpha,\beta) θD(α,β)=xminL(x,α,β),
乍一看,是不是与上一节原始无约束问题 θ p \theta_p θp很相似?是的,区别在于, θ p \theta_p θp是关于 x x x的最大化问题, θ D \theta_D θD是关于 α , β \alpha,\beta α,β的优化问题,所以是一个关于 α , β \alpha,\beta α,β的函数。
考虑此函数的极大化
m
a
x
α
,
β
:
α
i
≥
0
θ
D
(
α
,
β
)
=
m
a
x
α
,
β
:
α
i
≥
0
m
i
n
x
L
(
x
,
α
,
β
)
\mathop{max}\limits_{\alpha,\beta:\alpha_i\ge0}\theta_D(\alpha,\beta)=\mathop{max}\limits_{\alpha,\beta:\alpha_i\ge0}\mathop{min}\limits_{x}L(x,\alpha,\beta)
α,β:αi≥0maxθD(α,β)=α,β:αi≥0maxxminL(x,α,β) (1)
而上一节拉格朗日函数处理原始约束问题得到的结果
m
i
n
x
θ
p
(
x
)
=
m
i
n
x
m
a
x
α
,
β
:
α
i
≥
0
L
(
x
,
α
,
β
)
=
m
i
n
x
(
x
)
\mathop{min}\limits_x\theta_p(x)=\mathop{min}\limits_{x}\mathop{max}\limits_{\alpha, \beta:\alpha_i\ge0}L(x,\alpha,\beta) = \mathop{min}\limits_x(x)
xminθp(x)=xminα,β:αi≥0maxL(x,α,β)=xmin(x) (2)
式(1)与式(2)构成对偶关系,形式上可以看出很对称,只不过:
- 原始问题是先固定 L ( x , α , β ) L(x, \alpha, \beta) L(x,α,β)中的 x x x, 先优化出 α , β \alpha,\beta α,β,再优化 x x x;
- 而对偶问题则先固定 α , β \alpha,\beta α,β,优化出 x x x, 再确定参数 α , β \alpha,\beta α,β;
定义对偶问题的最优值:
d
∗
=
m
a
x
α
,
β
:
α
i
≥
0
θ
D
(
α
,
β
)
d^*=\mathop{max}\limits_{\alpha,\beta:\alpha_i\ge0}\theta_D(\alpha,\beta)
d∗=α,β:αi≥0maxθD(α,β)
原始问题与对偶问题的关系
对任意的
α
,
β
,
x
\alpha,\beta,x
α,β,x,有如下的关系
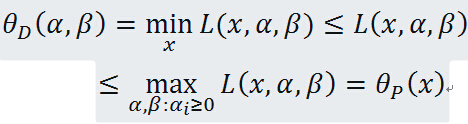
即

由于原始问题与对偶问题都有最优值,所以
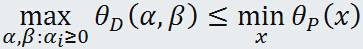
即得到如下定理:
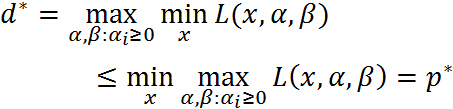
也就是说原始问题的最优值≥对偶问题的最优值,但是我们要通过对偶问题来求解原始问题,就必须使得原始问题的最优值与对偶问题的最优值相等,于是可以得出下面的推论:
推论:设 x ∗ , α ∗ , β ∗ x^*,\alpha^*,\beta^* x∗,α∗,β∗分别是原始问题和对偶问题的可行解,如果 d ∗ = p ∗ d^*=p^* d∗=p∗,那么 x ∗ , α ∗ , β ∗ x^*,\alpha^*,\beta^* x∗,α∗,β∗分别是原始问题和对偶问题的最优解。
所以,当原始问题和对偶问题的最优值相等: d ∗ = p ∗ d^*=p^* d∗=p∗时,可以用求解对偶问题来求解原始问题(当然是对偶问题求解比直接求解原始问题简单的情况下),
但是到底满足什么样的条件才能使的呢,这就是下面要阐述的 KKT 条件
四、KKT条件
前言:只要满足KKT条件,就可利用上节拉格朗日对偶问题来求解原始问题
KKT条件如下:

总结
简而言之,若遇到原始带约束的问题,可采用如下方法进行优化
参考文章
感谢这篇博主的分享《简易解说拉格朗日对偶》
https://www.cnblogs.com/90zeng/p/Lagrange_duality.html























 3808
3808











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








