电子电工基础：从理论到实践的全面解析

前言

电子电工基础是电子工程和电气工程学科的基石。无论是从事硬件设计、嵌入式系统开发，还是电力系统分析，掌握电子电工基础知识都是必不可少的。本文将从基础知识入手，逐步深入，并通过实际案例和公式详细解析相关概念。

1. 直流电路

1.1 欧姆定律

欧姆定律是电子电工中最基本的定律之一，描述了电压、电流和电阻之间的关系。

公式：

V=I×RV=I×R

• V：电压（伏特，V）
• I：电流（安培，A）
• R：电阻（欧姆，Ω）

应用案例：

假设有一个简单的直流电路，电阻 R=10 ΩR=10Ω，电流 I=2 AI=2A，则电压 VV 为：

V=2 A×10 Ω=20 VV=2A×10Ω=20V

图1：欧姆定律示意图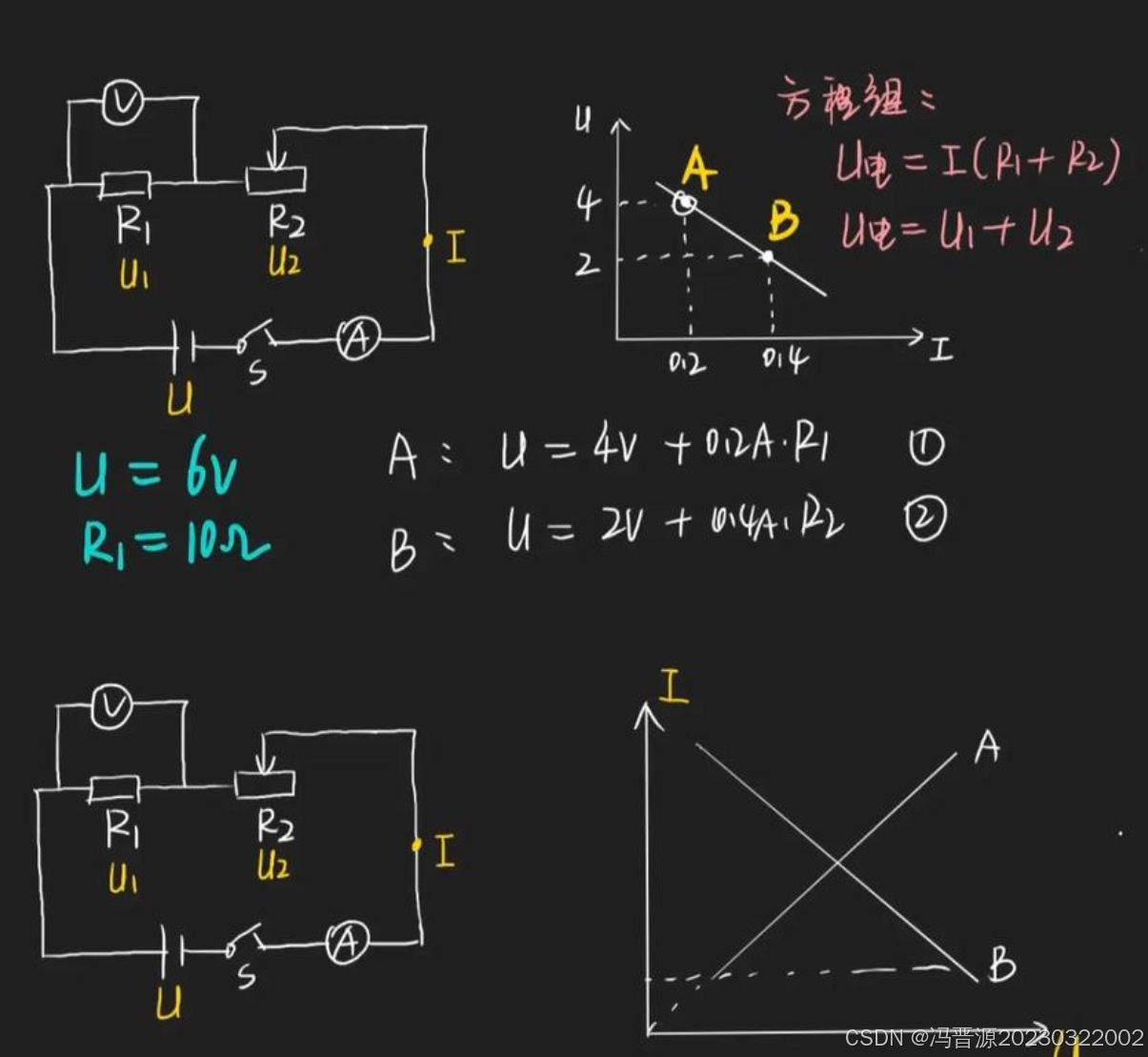

1.2 基尔霍夫定律

基尔霍夫定律包括基尔霍夫电流定律（KCL）和基尔霍夫电压定律（KVL）。

1.2.1 基尔霍夫电流定律（KCL）

公式：

∑Iin=∑Iout∑Iin​=∑Iout​

• ∑Iin∑Iin​ ：流入节点的电流总和
• ∑Iout∑Iout​ ：流出节点的电流总和

应用案例：

在一个节点处，流入的电流为 3 A3A 和 5 A5A，流出的电流为 4 A4A 和 4 A4A，则：

3 A+5 A=4 A+4 A3A+5A=4A+4A

验证：8 A=8 A8A=8A

1.2.2 基尔霍夫电压定律（KVL）

公式：

∑V=0∑V=0

• ∑V∑V ：回路中电压降的总和

应用案例：

在一个回路中，电压源 Vs=12 VVs​=12V，电阻 R1=4 ΩR1​=4Ω 和 R2=2 ΩR2​=2Ω 的电压降分别为：

V1=I×R1V1​=I×R1​
V2=I×R2V2​=I×R2​

根据 KVL：

Vs−V1−V2=0Vs​−V1​−V2​=0

假设电流 I=2 AI=2A，则：

V1=2 A×4 Ω=8 VV1​=2A×4Ω=8V
V2=2 A×2 Ω=4 VV2​=2A×2Ω=4V

验证：

12 V−8 V−4 V=012V−8V−4V=0

图2：基尔霍夫定律示意图

2. 交流电路

2.1 交流电的基本概念

交流电（AC）是电流和电压随时间周期性变化的形式。交流电的主要参数包括频率、周期、幅值和相位。

公式：

v(t)=Vmsin⁡(ωt+ϕ)v(t)=Vm​sin(ωt+ϕ)

• v(t)v(t) ：瞬时电压
• VmVm​ ：电压幅值
• ωω ：角频率（ω=2πfω=2πf）
• ff ：频率
• ϕϕ ：相位角

2.2 阻抗

阻抗（Z）是交流电路中电阻、电感和电容的综合效应。

公式：

Z=R+jXZ=R+jX

• ZZ ：阻抗
• RR ：电阻
• XX ：电抗（X=XL−XCX=XL​−XC​）
• XL=ωLXL​=ωL ：电感电抗
• XC=1ωCXC​=ωC1​ ：电容电抗

应用案例：

假设一个电路中，电阻 R=3 ΩR=3Ω，电感 L=0.01 HL=0.01H，电容 C=0.001 FC=0.001F，频率 f=50 Hzf=50Hz，则：

XL=2π×50 Hz×0.01 H=3.14 ΩXL​=2π×50Hz×0.01H=3.14Ω
XC=12π×50 Hz×0.001 F=3.18 ΩXC​=2π×50Hz×0.001F1​=3.18Ω
X=XL−XC=3.14 Ω−3.18 Ω=−0.04 ΩX=XL​−XC​=3.14Ω−3.18Ω=−0.04Ω
Z=R+jX=3 Ω−0.04 j ΩZ=R+jX=3Ω−0.04jΩ

图3：交流电路阻抗示意图

3. 实际应用

3.1 电源设计

在电源设计中，需要考虑电压、电流、功率和效率等因素。例如，设计一个线性稳压器，需要选择合适的稳压芯片，并根据负载电流和电压降计算散热需求。

公式：

线性稳压器的效率：

η=PoutPin=Vout×IoutVin×Iinη=Pin​Pout​​=Vin​×Iin​Vout​×Iout​​

应用案例：

设计一个输出电压 Vout=5 VVout​=5V，输出电流 Iout=1 AIout​=1A 的线性稳压器，假设输入电压 Vin=12 VVin​=12V，则效率为：

η=5 V×1 A12 V×1.1 A≈0.379=37.9%η=12V×1.1A5V×1A​≈0.379=37.9%

3.2 滤波器设计

滤波器用于滤除不需要的频率成分。常见的滤波器类型包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。

滤波器设计是电子电工基础中的一个重要部分，广泛应用于信号处理、通信系统、音频处理等领域。本文将详细介绍滤波器的分类、设计方法以及实际应用，并通过公式和电路图进行深入解析。

1. 滤波器概述

滤波器是一种选频电路，用于去除或保留特定频率范围的信号。根据其功能，滤波器主要分为以下几类：

• 低通滤波器（Low-Pass Filter, LPF）：允许低于截止频率的信号通过，抑制高于截止频率的信号。
• 高通滤波器（High-Pass Filter, HPF）：允许高于截止频率的信号通过，抑制低于截止频率的信号。
• 带通滤波器（Band-Pass Filter, BPF）：允许特定频率范围的信号通过，抑制其他频率的信号。
• 带阻滤波器（Band-Stop Filter, BSF）：抑制特定频率范围的信号，允许其他频率的信号通过。

2. 滤波器设计基础

2.1 传递函数

滤波器的传递函数 H(s)H(s) 描述了输入信号与输出信号之间的关系。对于无源滤波器，传递函数通常表示为：

H(s)=Vout(s)Vin(s)H(s)=Vin​(s)Vout​(s)​

其中，s=jωs=jω 是复频率。

2.2 截止频率

截止频率 fcfc​ 是滤波器开始显著衰减或通过的频率点。对于低通和高通滤波器，截止频率是3dB衰减点。

公式：

低通滤波器的截止频率：

fc=12πRCfc​=2πRC1​

高通滤波器的截止频率：

fc=12πRCfc​=2πRC1​

3. 无源滤波器设计

3.1 低通滤波器

电路图：

公式：

传递函数：

H(s)=11+sRCH(s)=1+sRC1​

幅频响应：

∣H(jω)∣=11+(ωRC)2∣H(jω)∣=1+(ωRC)2

​1​

设计步骤：

1.确定截止频率 fcfc​。

2.选择合适的电阻 RR 和电容 CC 值，使得 fc=12πRCfc​=2πRC1​。

公式：

低通滤波器的截止频率：

fc=12πRCfc​=2πRC1​

应用案例：

设计一个截止频率为 1000 Hz1000Hz 的低通滤波器，选择电容 C=0.1 μFC=0.1μF，则电阻 RR 为：

R=12π×1000 Hz×0.1 μF=1.59 kΩR=2π×1000Hz×0.1μF1​=1.59kΩ