译:自适应损失平衡物理信息神经网络
-- Neurocomputing -- 2022
一、引言
鉴于PINN的损失函数的各个权重是固定的,并且也有研究观察到PINN的训练效率敏感地依赖于与不同损失项相关的权重。但是一般的调整损失权重的方法非常耗时、费力,而且容易出现错误和遗漏。所以作者希望找到一种更方便的自适应学习损失权值的方法——自适应损失平衡物理信息神经网络(IbPINNs)。
二、方法
2.1、动机
首先PINN的损失是:

其中损失权重λ大小是固定的,以及

作者通过数值实验研究了损失权值对PINN精度的影响。这里演示通过表1中具有不同损失权的PINN学习一维泊松方程的结果。

误差曲线如图2所示:

很明显,PINN的性能受损失权值选择的影响。因此,需要提出一种更方便的方法来自适应学习这些损失权值,从而提高PINN的精度和鲁棒性。
2.2、IbPINNs
作者建立了一个输出为u的高斯概率模型。高斯似然被定义为带均值的高斯,由PINN和不确定性参数近似:

基于最小化目标,最小化模型的负对数似然:
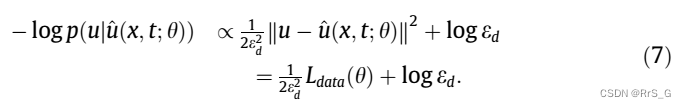
同样,也可以建立一个输出为g或h的高斯概率模型来定义PINN的BC和IC损失。进一步,假设高斯概率模型的输出包括两个向量u, g,每个都遵循一个高斯分布:
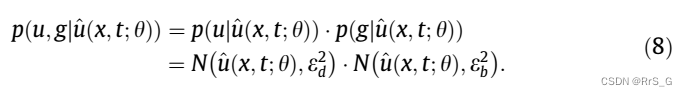
这就引出了多输出模型的最小化目标:

因此,作者建立了四个向量的多输出模型来定义损失函数。自适应损失平衡PINN(IbPINNs)的损失函数可以表示为:
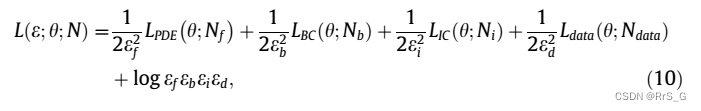
一方面,当自适应权重降低时,总权重
增加,这意味着对
的惩罚更大;另一方面,最后一项
可以防止自适应权重下降太多。一般来说,较大的自适应权值会降低损失项的贡献,而较小的自适应权值会增加其贡献并对模型造成惩罚。即自动调整各损失项的自适应权重的方法。
对上述损失做一下变换:

通过指数映射,可以使损失函数的最小化不受约束。由于exp(-s)解析为正域,自适应权值不会很快收敛到零。训练会在数值上更加稳定。ibpinn的示意图如图3所示。方法总结为算法一。


三、实验
二维泊松方程

结果:

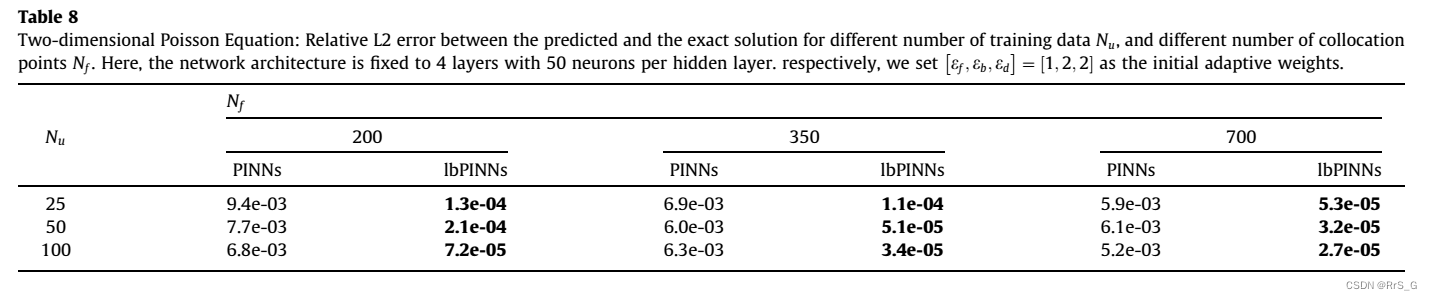







 本文介绍了自适应损失平衡物理信息神经网络(IbPINNs),解决PINN训练中固定损失权重的问题。研究发现PINN的性能高度依赖于损失权重的选择。IbPINNs通过建立高斯概率模型,自适应调整损失项权重,以提高模型的精度和鲁棒性。实验结果展示了该方法在二维泊松方程求解中的有效性。
本文介绍了自适应损失平衡物理信息神经网络(IbPINNs),解决PINN训练中固定损失权重的问题。研究发现PINN的性能高度依赖于损失权重的选择。IbPINNs通过建立高斯概率模型,自适应调整损失项权重,以提高模型的精度和鲁棒性。实验结果展示了该方法在二维泊松方程求解中的有效性。
















 5389
5389

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








