机器学习笔记系列
- 回归笔记：机器学习-回归算法笔记
- 分类笔记：机器学习-分类算法笔记
- 神经网络笔记：机器学习-神经网络算法笔记
- 朴素贝叶斯笔记：机器学习-朴素贝叶斯分类算法笔记
无监督学习
含义
- 给算法一个数据集，但是不给算法任何其他的信息，例如对错等，让算法自行分组
聚类
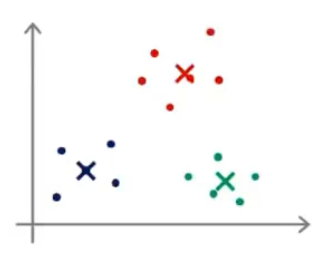
- 目的是自动从给定的数据集中自动分析其特征，并将其自动的分成一个个的簇
K-均值算法
介绍
-
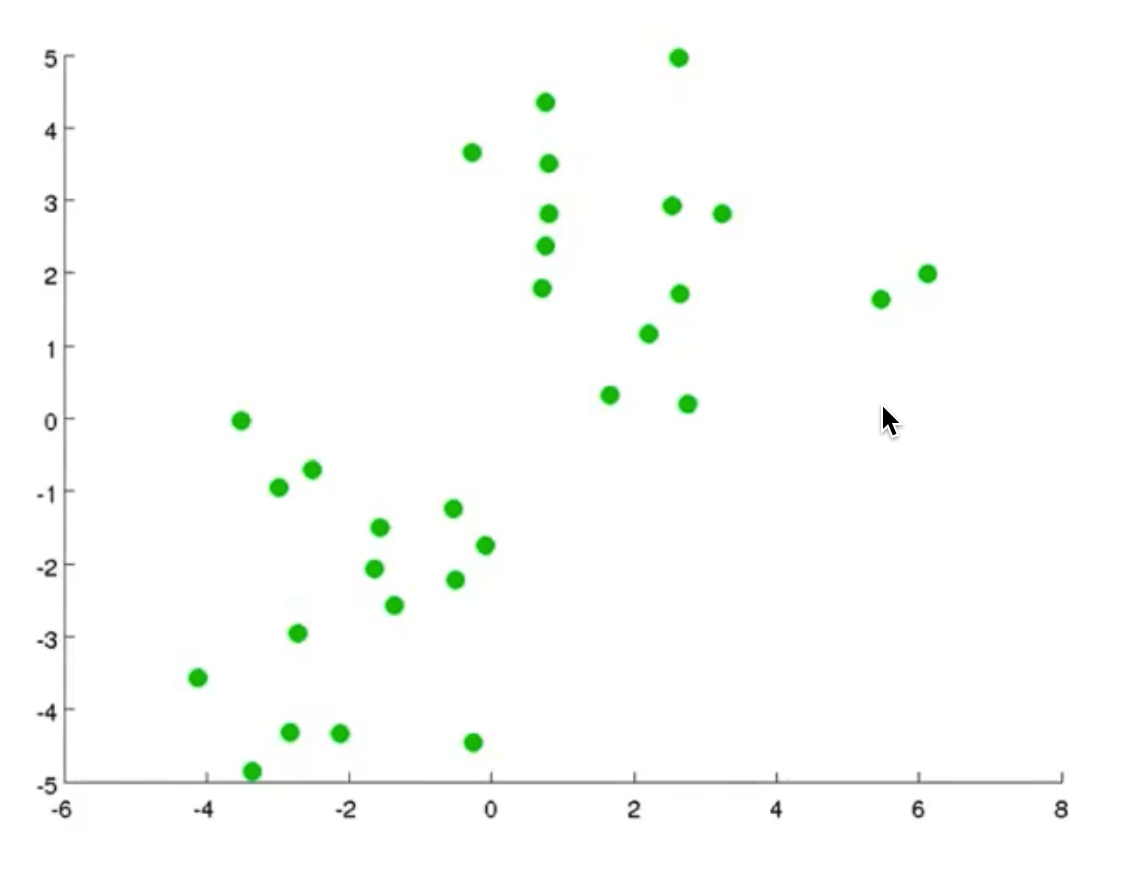
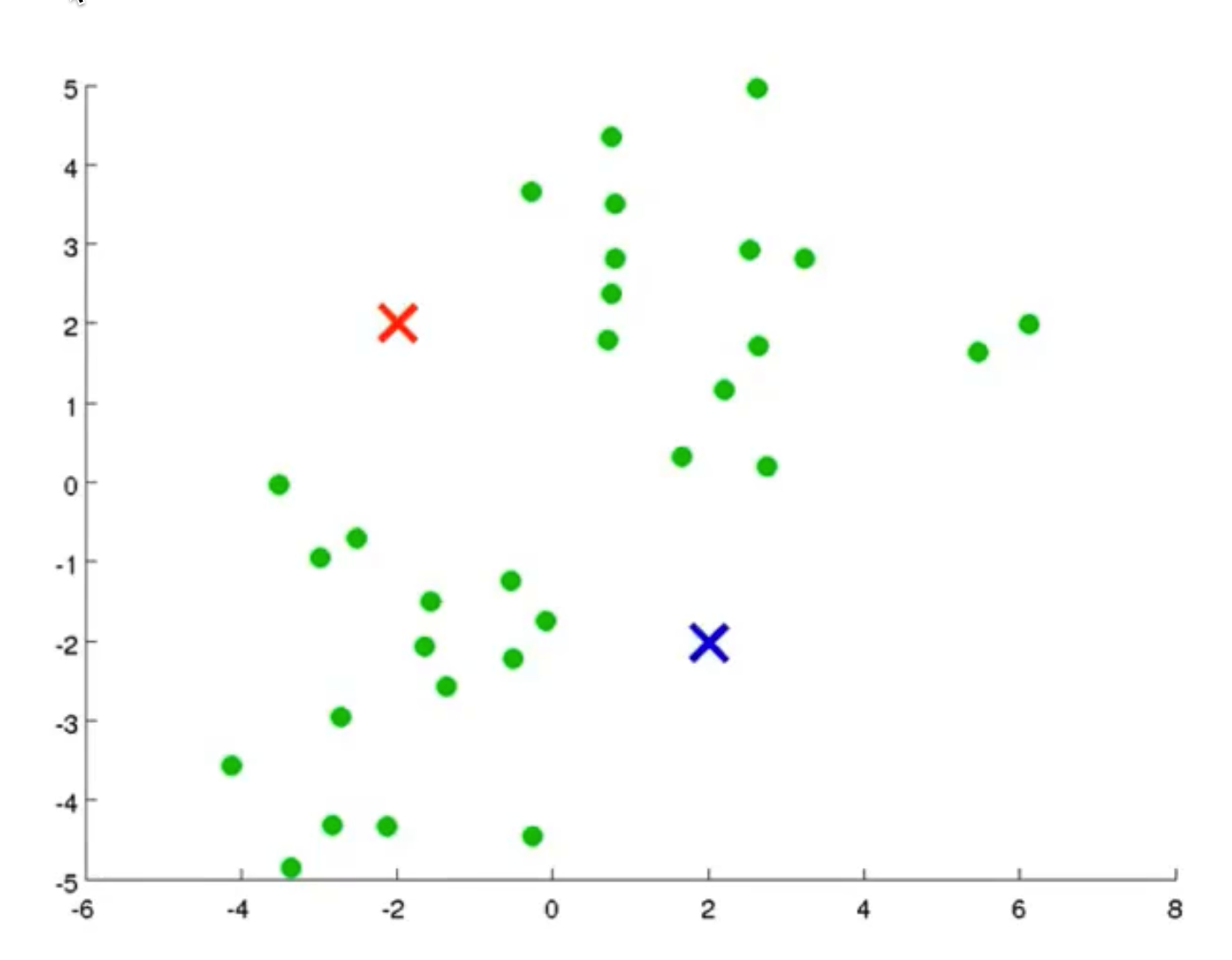
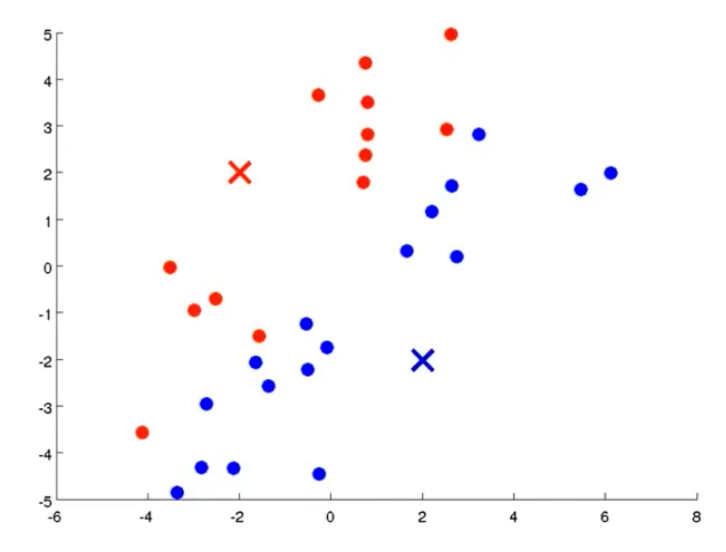
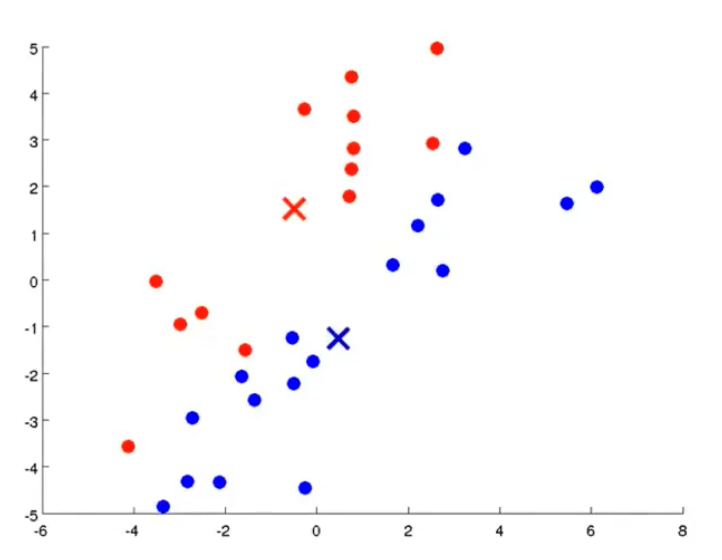
我们先想好要将整个数据集分为几个簇，若为K个簇，则分配K个聚类中心，将每个聚类中心随机分配一个数值，每个聚类中心的每次迭代都将比较所有样本和自己的距离，将离自己近的样本划分为自己的类别，然后计算自己类别下的所有样本的均值赋值给自己，再更新位置，最终碰到更新不动了，则划分完成，如下列步骤所示
-
-
-
-
-
-
-
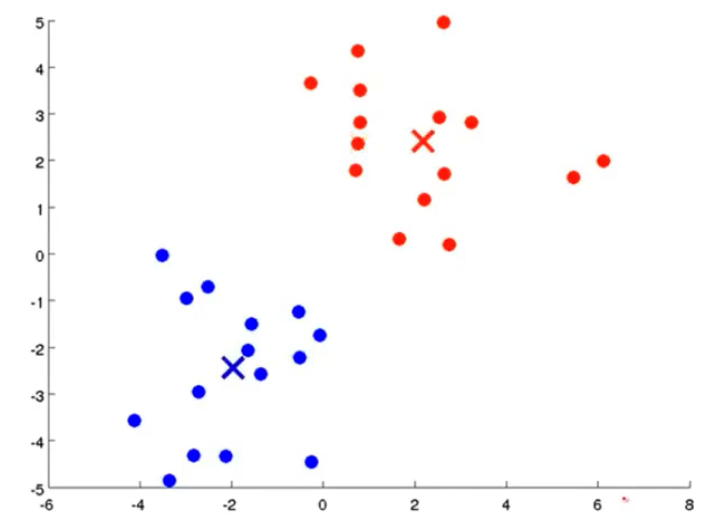
从上示图例可以清楚的看见两个聚类中心所移动的走向及其步骤的
大体步骤
- 输入：
- K个值（代表想要分成的簇的个数）
- 训练集
- 根据输入的K值随机确定 μ 1 , μ 2 , . . . , μ K ∈ R n \mu_1,\mu_2,...,\mu_K\in\mathbb{R}^n μ1,μ2,...,μK∈Rn个簇
- 递归（当聚类中心停止移动时跳出循环）
- for i in range(1, m) m代表样本的个数
- 计算出每个样本离每个聚类中心之间的距离，然后将其赋值给 c ( i ) c^{(i)} c(i)
- 例如： c ( 1 ) = 2 c^{(1)}=2 c(1)=2 的意思为第一个样本离2号聚类中心最近，属于2号聚类中心
- 计算样本与聚类中心的距离公式： ∥ x ( i ) − μ k ∥ 2 \left \| x^{(i)}-\mu_k \right \| ^2 x(i)−μk 2
- 该式可以不加平方，效果也是一样的，但是由于大家的公约都是加平方，所以我们这也加上平方
- for k in range(1, K)
- 计算每个聚类中心名下的所有样本的均值赋值给该聚类中心，移动聚类中心的位置
- for i in range(1, m) m代表样本的个数
一个问题
- 若划分完簇后，发现有聚类中心并没有任何样本怎么办，有两个方法
- 删除该聚类中心（常见做法）
- 重新随机聚类中心的数值位置，再进行迭代计算
优化目标函数（代价函数）
- 先定义几个符号
- c ( i ) c^{(i)} c(i) ：第i个样本所属的簇
- μ k \mu_k μk ：第k个簇
-
μ
c
(
i
)
\mu_{c^{(i)}}
μc(i) ：第i个样本所属的簇的聚类中心
- 例如，当 c ( 1 ) = 2 c^{(1)}=2 c(1)=2 时代表第一个样本属于2号簇，而 μ c ( 1 ) = μ 2 \mu_{c^{(1)}}=\mu_2 μc(1)=μ2
- 优化目标函数： J ( c ( 1 ) , . . . , c ( m ) , μ 1 , . . . , μ K ) = 1 m ∑ i = 1 m ∥ x ( i ) − μ c ( i ) ∥ 2 J(c^{(1)},...,c^{(m)},\mu_1,...,\mu_K)=\frac{1}{m}\sum\limits_{i=1}^{m}\left\|x^{(i)}-\mu_{c^{(i)}}\right\|^2 J(c(1),...,c(m),μ1,...,μK)=m1i=1∑m x(i)−μc(i) 2
- 不难看出，sum后面的就是我们的距离公式，该函数也就是要寻找出能使得该函数最小化的 c ( 1 ) , . . . , c ( m ) , μ 1 , . . . , μ K c^{(1)},...,c^{(m)},\mu_1,...,\mu_K c(1),...,c(m),μ1,...,μK
- 该函数也叫失真代价函数｜K均值算法的失真
初始化聚类中心
- 在初始化聚类中心之前我们首先需要确定我们的K值，一般情况下，K<m
- 因为你想想，m是样本个数，K是我们想要将该样本分类的个数，所以K<m
- 如何随机选择我们的聚类中心呢？
- 我们可以随机挑选K个样本，然后使我们的K个聚类中心等于这K个样本
- 也就如图所示
-
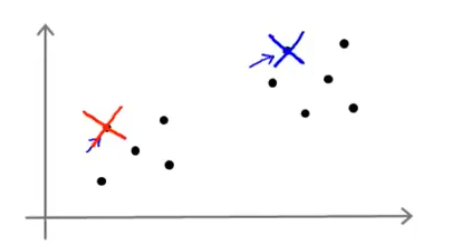
- 可以看到我们随机将我们的两个聚类中心放在了我们的两个样本上
- 但是我们可以发现一个问题，上图中是刚好将两个聚类中心随机到了两坨样本上
- 但是如果运气不好的话，就有可能出现如下情况
-
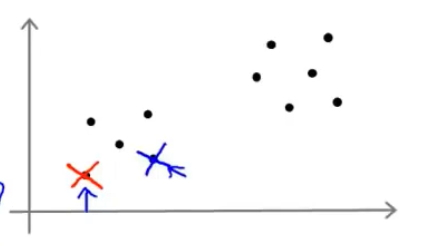
- 可以看到两个聚类中心在一坨样本当中，这样经过K均值算出的结果肯定和上图是不一样的
- 那么我们就陷入了局部最优的情况，那么我们怎样得出全局最优呢？
局部最优及全局最优
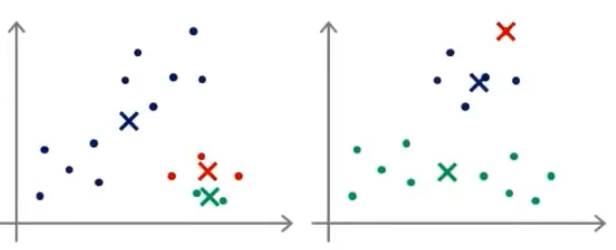
- 我们再来举个栗子
-
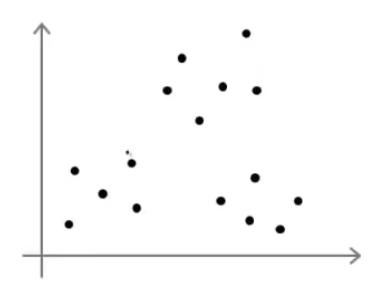
- 当我们有一个这样子的样本图，我们假设要将其分成3个簇
- 那么我们可能得出以下的三种结果
- 全局最优
-
- 局部最优
-
- 全局最优
- 这个主要的原因就在于初始化聚类中心不同的点所造成的
- 所以我们可以尝试多次初始化聚类中心，也就是运行多次K均值算法
- 一般运行K均值算法的次数为50-1000次
多次运行K均值步骤
- For i in range(1, 100) 运行100次K均值算法
- 随机初始化K均值聚类中心
- 运行K均值，获取 c ( 1 ) , . . . , c ( m ) , μ 1 , . . . , μ K c^{(1)},...,c^{(m)},\mu_1,...,\mu_K c(1),...,c(m),μ1,...,μK
- 计算代价函数J
- 经过上述运行后，我们可以得出100种分类该数据集的方法
- 我们最后从这100种方法中选择出代价函数J最小的那个方法
PS
- 一般情况下，当我们要分出的簇的个数较小，在10个以下的情况，我们运行多次初始化会有比较明显的效果，而如果K的值较大，例如100个以上，那么可能在第一次随机初始化的时候效果就比较好了，所以在给后续进行随机初始化的时候效果可能不会有很大的改进
- 一般情况下，当我们要分出的簇的个数较小，在10个以下的情况，我们运行多次初始化会有比较明显的效果，而如果k的值较大，例如100个以上，那么可能在第一次随机初始化的时候效果就比较好了，所以在给后续进行随机初始化的时候效果可能不会有很大的改进
参考链接
- https://www.bilibili.com/video/BV1FT4y1E74V/?spm_id_from=333.337.search-card.all.click&vd_source=97163a4e6e2704667559fdbd58743862
24
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
