机器学习 06：SMO 算法

概述

---

$SMO$ 是由 $Platt$ 在 1998 年提出的、针对软间隔最大化 $SVM$ 对偶问题求解的一个算法，其基本思想很简单：如果所有变量的解都满足此优化问题的 KKT 条件，则这个优化问题的解就得到了；否则在每一步优化中，挑选出诸多参数 ${\alpha }_k(k=1,2,\cdots ,n)$ 中的两个参数 ${\alpha }_i,{\alpha }_j$ 作为变量，其余参数都视为常数，问题就变成了类似于二次方程求最大值的问题，从而我们就能求出解析解，这两个变量中，一个是违反 KKT 条件最严重的那一个，另一个由约束条件自动确定一个。

选择变量的启发式方法

---

先来回顾一下 $SVM$ 中的优化目标函数：

$$\begin{gathered} \underset{{\alpha }_i\ge 0}{\min }\left(\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K({\vec{x}}_i,{\vec{x}}_j)-\sum _{i=1}^N{\alpha }_i\right) \\ s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0,0\le {\alpha }_i\le C \end{gathered}$$

由于要满足约束 $\sum _{i=1}^N{\alpha }_i{y}_i=0$，所以每次需要选取两个 ${\alpha }_i$ 做为变量，这一点与坐标上升法不同。

要使优化目标函数有解，我们需要使其满足 $KKT$ 条件中的互补松弛：

$${\alpha }_i(y_i(\vec{w}\cdot \varphi ({\vec{x}}_i)+b)-1+{\xi }_i)=0$$

根据上面的条件我们可以得出：

$$\{\begin{array}{ll}{y}_i(\vec{w}\cdot \varphi ({\vec{x}}_i)+b)\ge 1& {\alpha }_i=0\\ y_i(\vec{w}\cdot \varphi ({\vec{x}}_i)+b)=1& 0\le {\alpha }_i\le C\\ y_i(\vec{w}\cdot \varphi ({\vec{x}}_i)+b)\le 1& {\alpha }_i=C\end{array}$$

由于 $\vec{w}=\sum _{j=1}^N{\alpha }_j{y}_j\varphi ({\vec{x}}_j)$，我们令

$$g({\vec{x}}_i)=\vec{w}\cdot \varphi ({\vec{x}}_i)+b=\sum _{j=1}^N{\alpha }_j{y}_{j}K({\vec{x}}_i,{\vec{x}}_j)+b$$

则可以推出以下三个条件：

$$\{\begin{array}{ll}{y}_{i}g({\vec{x}}_i)\ge 1& {\alpha }_i=0\\ y_{i}g({\vec{x}}_i)=1& 0\le {\alpha }_i\le C\\ y_{i}g({\vec{x}}_i)\le 1& {\alpha }_i=C\end{array}$$

选择第一个变量

在 $SMO$ 中，我们称第一个变量为外循环。外循环取的是样本中违反 $KKT$ 条件最严重的点。

我们可以借助上面推出的条件来度量一个点违反 $KKT$ 条件的程度，具体来说，我们定义三份“差异向量”

$$\begin{gathered} {\vec{c}}^{(k)}=(c_1^{(k)},c_2^{(k)},\cdots ,c_N^{(k)}),k=1,2,3 \\ {c}_i^{(k)}=y_{i}g({\vec{x}}_i)-1 \end{gathered}$$

其中第 $k$ 个向量对应着第 $k$ 个条件。对于不同的条件，我们按不同方式将对应向量的某些位置置为 0。

• 第一个条件：${\alpha }_i=0\Rightarrow c_i^{(1)}\ge 0$ 若满足：

  • ${\alpha }_i>0$ 且 $c_i^{(1)}\le 0$
  • ${\alpha }_i=0$ 且 $c_i^{(1)}\ge 0$

• 第二个条件：$0\le {\alpha }_i\le C\Rightarrow c_i^{(2)}=0$ 若满足：

  • ${\alpha }_i=0$ 或 ${\alpha }_i=C$ 且 $c_i^{(2)}\ne 0$
  • $0\le {\alpha }_i\le C$ 且 $c_i^{(2)}=0$

• 第三个条件：${\alpha }_i=C\Rightarrow c_i^{(3)}\le 0$

  • ${\alpha }_i<C$ 且 $c_i^{(3)}\ge 0$
  • ${\alpha }_i=C$ 且 $c_i^{(3)}\le 0$

最后只需要将这三个差异向量的平方相加作为“损失”，从而直接选出损失最大的 ${\alpha }_i$ 作为外循环即可。

选择第二个变量

第二个变量成为内循环，只需要简单的随机选取一个即可。

取出这两个变量之后，把其它变量看做常数，这样优化目标函数就变成了带约束的二次规划问题。

目标函数的优化

---

假设选择的两个变量是 ${\alpha }_1,{\alpha }_2$，把其它的 ${\alpha }_i$ 都看作常数。定义 $K_{ij}=K({\vec{x}}_i,{\vec{x}}_j)$ 那么原先的优化目标函数就成了：
$$\begin{gathered} \underset{{\alpha }_1,{\alpha }_2}{\min }\frac{1}{2}{K}_{11}{\alpha }_1^2+\frac{1}{2}{K}_{2,2}{\alpha }_2^2+y_1{y}_2{K}_{1,2}{\alpha }_1{\alpha }_2-({\alpha }_1+{\alpha }_2)+y_1{\alpha }_1\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i,1}+y_2{\alpha }_2\sum _{i=3}^N{y}_i{\alpha }_i{K}_{i,2}+c \\ s.t.{\alpha }_1{y}_1+{\alpha }_2{y}_2=C \\ 0\le {\alpha }_i\le C,i=1,2 \end{gathered}$$

无约束求极值

我们先暂时不管约束条件 $0\le {\alpha }_i\le C,i=1,2$，通过 ${\alpha }_1=(C-{\alpha }_2{y}_2)y_1$ 可以将目标函数替换成单变量形式：
$$\min \varphi ({\alpha }_2)=\frac{1}{2}{K}_{1,1}(C-{\alpha }_2{y}_2{)}^2+\frac{1}{2}{K}_{2,2}{\alpha }_2^2+y_2{K}_{12}{\alpha }_2(C-{\alpha }_2{y}_2)-y_1(C-{\alpha }_2{y}_2)-{\alpha }_2+(C-{\alpha }_2{y}_2)\sum _{i=3}^N{\alpha }_i{y}_i{K}_{1,i}+y_2{\alpha }_2\sum _{j=3}^N{\alpha }_j{y}_j{K}_{2,j}+c$$

我们设更新前的值为 ${\alpha }_i^{old}$, 更新后的值为 ${\alpha }_i^{new}$，对目标函数进行一个偏导的求：
$$\frac{\partial \varphi ({\alpha }_2^{new})}{\partial {\alpha }_2^{new}}=(K_{1,1}+K_{2,2}-2K_{1,2}){\alpha }_2^{new}-K_{1,1}C{y}_2+K_{1,2}C{y}_2+y_1{y}_2-1-y_2\sum _{i=3}^N{\alpha }_i{y}_i{K}_{1,i}+y_2\sum _{j=3}^N{\alpha }_j{y}_j{K}_{2,j}=0$$

因为 SVM 中数据点的预测值为：$f({\vec{x}}_j)=\sum _{i=1}^N{\alpha }_i{y}_{i}K({\vec{x}}_i,{\vec{x}}_j)+b$ 因此有：

• $\sum _{i=3}^N{\alpha }_i{y}_i{K}_{1,i}=f({\vec{x}}_1)-{\alpha }_1^{new}{y}_1{K}_{1,1}-{\alpha }_2^{new}{y}_2{K}_{1,2}-b$
• $\sum _{i=3}^N{\alpha }_i{y}_i{K}_{2,i}=f({\vec{x}}_2)-{\alpha }_1^{new}{y}_1{K}_{1,2}-{\alpha }_2^{new}{y}_2{K}_{2,2}-b$

另有：$C={\alpha }_1^{old}{y}_1+{\alpha }_2^{old}{y}_2$

将上面三个式子带入偏导中并化简得：
$$(K_{1,1}+K_{2,2}-2K_{1,2}){\alpha }_2^{n}ew=(K_{1,1}+K_{2,2}-2K_{1,2}){\alpha }_2^{old}+y_2[(f({\vec{x}}_1)-y_1)-(f({\vec{x}}_2)-y_2)]$$

设 $\eta =K_{1,1}+K_{2,2}-2K_{1,2}$，则有：
$$\{\begin{array}{l}{\alpha }_2^{new}={\alpha }_2^{old}+\frac{y_2[(f({\vec{x}}_1)-y_1)-(f({\vec{x}}_2)-y_2)]}{\eta }\\ {\alpha }_1^{old}{y}_1+{\alpha }_2^{old}{y}_2={\alpha }_1^{new}{y}_1+{\alpha }_2^{new}{y}_2\end{array}$$

这样我们就求出了这两个变量在无约束情况下的解析解。

加入约束

当 $y_1\ne y_2$ 时，线性限制条件可以写成：${\alpha }_1-{\alpha }_2=k$，根据 $k$ 的正负可以得到不同的上下界，可以统一表示为：

• 下界：$L=\max (0,{\alpha }_2-{\alpha }_1)$
• 上界：$H=\min (C,C+{\alpha }_2-{\alpha }_1)$

当 $y_1=y_2$ 时，限制条件可以写成：${\alpha }_1+{\alpha }_2=k$，此时上下界可以统一为：

• 下界：$L=max(0,{\alpha }_1+{\alpha }_2-C)$
• 上界：$H=min(C,{\alpha }_1+{\alpha }_2)$

由此可知，此约束为方形约束，下图为它的限制区域。

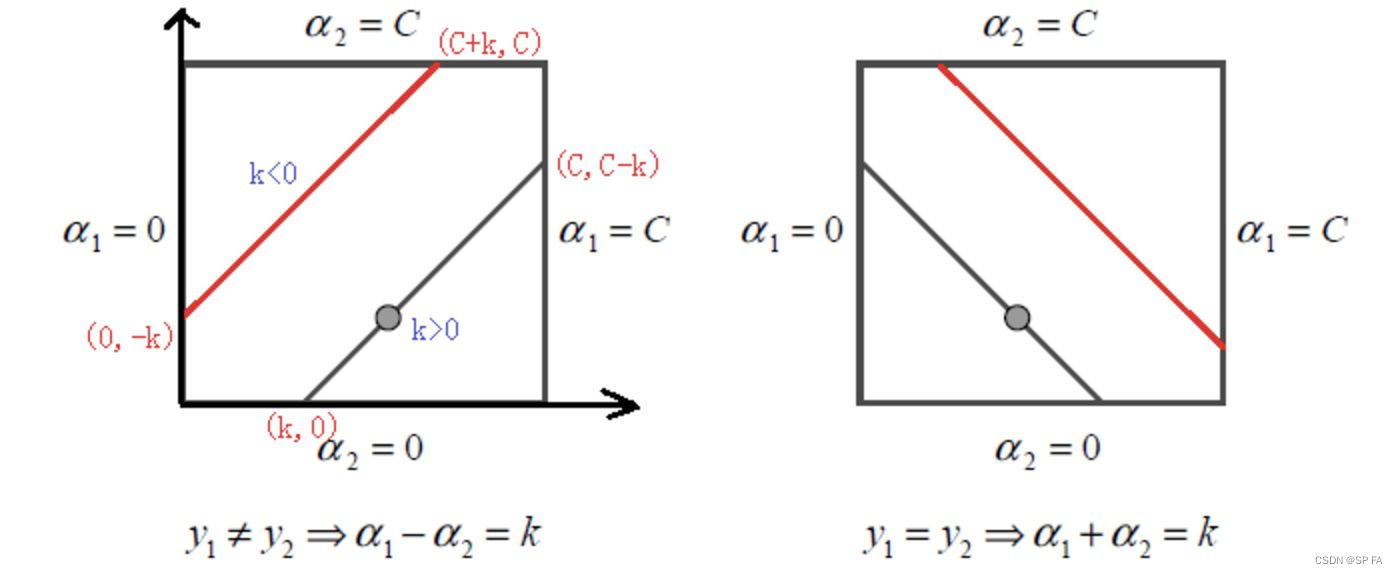
根据得到的上下界，我们可知加入约束后的 ${\alpha }_2^{new}$ 为：
$${\alpha }_2^{new}=\{\begin{array}{ll}H& {\alpha }_2^{new}>H\\ a_2^{new}& L\le {\alpha }_2^{new}\le H\\ L& {\alpha }_2^{new}<L\end{array}$$

这样就实现了对 ${\alpha }_i,{\alpha }_j$ 的更新。

更新阈值 b

---

每次更新完一对 ${\alpha }_i,{\alpha }_j$ 之后都需要重新计算阈值 $b$，因为它关系到 $f(\vec{x})$ 的计算和优化时误差 $E_i$ 的计算。

当 $0<alph{a}_1^{new}<C$，根据 $KKT$ 条件可知相应的数据点为支持向量，满足 $y_1(w^T+b)=1$，两边同时乘 $y_1$ 得：$\sum _{i=1}^N{\alpha }_i{y}_i{K}_{i,1}+b=y_1$，因此 $b_1^{new}$ 的值为：
$$b_1^{new}=y1-\sum _{i=3}^N{\alpha }_i{y}_i{K}_{i,1}-{\alpha }_1^{new}{y}_1{K}_{1,1}-{\alpha }_2^{new}{y}_2{K}_{2,1}$$

其中，$y1-\sum _{i=3}^N{\alpha }_i{y}_i{K}_{i,1}=-E_1+{\alpha }_1^{old}{y}_1{K}_{1,1}+{\alpha }_2^{old}{y}_2{K}_{2,1}+b^{old}$

当 $0<{\alpha }_2^{new}<C$ 时：
$$b_2^{new}=-E_2-y_1{K}_{1,2}({\alpha }_1^{new}-{\alpha }_1^{old})-y_2{K}_{2,2}({\alpha }_2^{new}-{\alpha }_2^{old})+b^{old}$$

当 $b_1,b_2$ 都有效时他们是相等的，即 $b^{new}=b_1^{new}=b_2^{new}$
当 ${\alpha }_1,{\alpha }_2$ 都在边界上，且 $L\ne H$ 时，选择它们的中点作为新的阈值：$b^{new}=\frac{b_1^{new}+b_2^{new}}{2}$

同步更新于：SP-FA 的博客

---

返回