第一题:
sum
sum Accepts: 640 Submissions: 1744
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
问题描述
给定一个数列,求是否存在连续子列和为m的倍数,存在输出YES,否则输出NO
输入描述
输入文件的第一行有一个正整数T(1≤T≤10),表示数据组数。
接下去有T组数据,每组数据的第一行有两个正整数n,m ( 1≤n≤100000 , 1≤m≤5000).
第二行有n个正整数x (1≤x≤100)表示这个数列。
输出描述
输出T行,每行一个YES或NO。
输入样例
2
3 3
1 2 3
5 7
6 6 6 6 6
输出样例
YES
NO
官方题解:
预处理前缀和,一旦有两个数模m的值相同,说明中间一部分连续子列可以组成m的倍数。 另外,利用抽屉原理,我们可以得到,一旦n大于等于m,答案一定是YES 复杂度 O(n)
分析:
首先用记录所有的前缀和sum[i](a[1]+..+a[i])。所以a[i]+…+a[j]=sum[j]-sum[i-1]。如果a[i]+..+a[j]是m的倍数的话,那么sum[i-1]%m一定等于sum[j]%m。所以我们只能判断在所有前缀和中是否存在sum[i],sum[j]模m后相等即可。
AC代码:
#include <iostream>
#include <cstring>
#include <cstdio>
#define maxn 100005
using namespace std;
int T,n,m,a[maxn],sum[maxn];
bool vis[5005];
int main()
{
scanf("%d",&T);
while (T--)
{
memset(vis,0,sizeof(vis));
memset(a,0,sizeof(a));
memset(sum,0,sizeof(sum));
scanf("%d%d",&n,&m);
bool f=0;
for (int i=1;i<=n;i++) scanf("%d",&a[i]);
for (int i=1;i<=n;i++)
{
sum[i]=a[i]+sum[i-1];
sum[i]%=m;
if (sum[i]==0)
{
f=1;
break;
}
}
if (f)
{
printf("YES\n");
continue ;
}
for (int i=1;i<=n;i++)
if (!vis[sum[i]]) vis[sum[i]]=1;
else
{
f=1;
break;
}
if (f) printf("YES\n");
else printf("NO\n");
}
return 0;
}
第二题:
domino
Accept: 0 Submit: 0
Time Limit: 2000/1000 MS (Java/Others) Memory Limit : 131072/131072 K (Java/Others)
小白在玩一个游戏。桌子上有n张多米诺骨牌排成一列。它有k次机会,每次可以选一个还没有倒的骨牌,向左或者向右推倒。每个骨
牌倒下的时候,若碰到了未倒下的骨牌,可以把它推倒。小白现在可以随意设置骨牌的高度,但是骨牌高度为整数,且至少为1,并且
小白希望在能够推倒所有骨牌的前提下,使所有骨牌高度的和最小。
Input:
第一行输入一个整数T(1≤T≤10)
每组数据有两行
第一行有两个整数n和k,分别表示骨牌张数和机会次数。(2≤k,n≤100000)
第二行有n-1个整数,分别表示相邻骨牌的距离d,1≤d≤100000
Output:
对于每组数据,输出一行,最小的高度和
输入样例
1
4 2
2 3 4
输出样例
9
官方题解:
首先骨牌只要考虑都往右推,其次能带倒骨牌的前提是高度大于等于距离+1。所以如果推一次,那么就是骨牌高度=离下一块骨牌距离+1. 把第一块左边距离设为无穷大,能推nk次,那么就是找nk块左边距离最大的向右推倒即可,所以只需要排序找到前nk-1大的距离。 有个小trick,推的次数可能大于骨牌数量 复杂度 O(nlogn)
分析:
一个骨牌想撞到旁边的骨牌,那么他的高度最小一定是它们之间的距离+1。(左推和右推一样,所以我们只需要考虑左推)。如果只有一个次机会推骨牌,那么第i个骨牌一定是它离右边的骨牌的距离+1,最后一个骨牌高度为1。现在有k次机会,那么我们可以把这一列骨牌分为k段,进行上述处理。那么我们怎么分段呢?分段其实就是可以不算一段距离,所以我们只要不算距离最大的k-1个距离即可。所以我们只需要sort()一次就可以了。
AC代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn=100010;
int a[maxn];
int main()
{
int t,n,k;
scanf("%d",&t);
while(t--)
{
scanf("%d%d",&n,&k);
for(int i=0;i<n-1;i++)
{
scanf("%d",&a[i]);
}
if(k>=n)
{
printf("%I64d\n",n);
continue;
}
long long ans=n;
sort(a,a+n-1);
for(int i=0;i<n-k;i++)
ans+=a[i];
printf("%I64d\n",ans);
}
return 0;
}
第三题:
abs
Accepts: 136 Submissions: 927
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 131072/131072 K (Java/Others)
问题描述
给定一个数x,求正整数y≥2,使得满足以下条件:
1.y-x的绝对值最小
2.y的质因数分解式中每个质因数均恰好出现2次。
输入描述
第一行输入一个整数T ( 1≤T≤50)
每组数据有一行,一个整数x ( 1≤x≤10^18)
输出描述
对于每组数据,输出一行y-x的最小绝对值
输入样例
5
1112
4290
8716
9957
9095
输出样例
23
65
67
244
70
官方题解:
由于y质因数分解式中每个质因数均出现2次,那么y是一个完全平方数,设y=z*z,题目可转换成求z,使得每个质因数出现1次. 我们可以暴力枚举z,检查z是否符合要求,显然当z是质数是符合要求,由素数定理可以得,z的枚举量在logn级别 复杂度
分析:
观察条件2
因为每个质因数恰好出现2次,所以y必定是一个平方数
假设y=z*z
那么z必定是一个由不同质数构成,且每种质数仅有一个的10^9以内的整数
思来想去,貌似没有什么特别优化的做法,那就暴力来一发
对于一个10^9范围内的数,若它在
显然,z为质数时也是满足的
那么我们就从sqrt(x)开始,分别向下,向上枚举,直到找到符合题意的z,哪个|y-x|小就取哪个
特判x<4的情况,因为题目规定y>=2
AC代码:
#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<math.h>
#include<vector>
#include<map>
#include<set>
#include<cmath>
#include<complex>
#include<string>
#include<algorithm>
#include<iostream>
#define eps 1e-8
#define LL long long
#define bitnum(a) __builtin_popcount(a)
using namespace std;
const int N = 50005;
int prime[N],p;
bool v[N];
void get_prime()
{
memset(v,false,sizeof(v));
p=0;
for(int i=2;i<N;i++)
{
if(!v[i])
{
prime[p++]=i;
for(int j=i+i;j<N;j+=i)
v[j]=true;
}
}
}
bool judge(__int64 x)
{
int k;
for(int i=0;i<p;i++)
{
k=0;
while(x%prime[i]==0)
{
k++;
x/=prime[i];
if(k>=2)
return false;
}
}
return true;
}
int main()
{
get_prime();
int t;
__int64 x,k,ans;
scanf("%d",&t);
while(t--)
{
scanf("%I64d",&x);
if(x<4)
{
printf("%I64d\n",4-x);
continue;
}
k=(__int64)sqrt(1.0*x);
int j;
for(j=0;;j--)
if(judge(k+j)) break;
ans=abs(x-(k+j)*(k+j));
for(j=1;;j++)
if(judge(k+j)) break;
ans=min(ans,abs(x-(k+j)*(k+j)));
printf("%I64d\n",ans);
}
return 0;
}








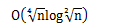














 848
848

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








