手撕代码
- 手撕mha
- 手撕transformer
- 手撕vit
- 只用numpy手撕mlp
手撕多头注意力,问transformer八股,问代码步骤,问时间复杂度以及如何优化
hot 100的medium(思路+代码)
树的层次遍历
力扣:最大公共子序列
二维0-1数组的最大全1正方形面积
八股重点是transformer八股
用 O ( n ) 的 时 间 复 杂 度 实 现 窗 口 为 k 的 maxpoolingld ( 滑 动 窗 口 + 双 端 队 列 )
八股
-
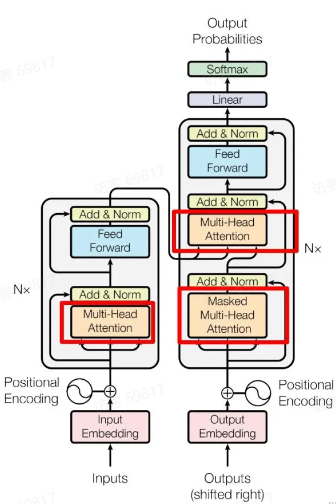
Transformer数据输入和处理的流程
先做embedding(图像patch embedding)–> 添加位置信息(Positional Encoding)–> 自注意力机制 --> 多头注意力机制 --> 前馈神经网络(FFN)–> 残差连接和LN- Encoder block 包含一个 Multi-Head Attention
- Decoder block 包含两个 Multi-Head Attention(其中有一个用到Masked)
- Multi-Head Attention 上方还包括一个 Add & Norm 层
- Add 表示残差链接(Residual Connection)用于防止网络退化
- Norm 表示 Layer Normalization,用于对每一层的激活值进行归一化
-
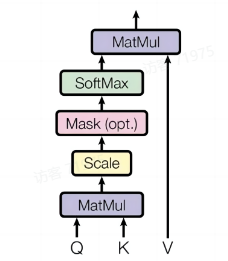
Self-Attention 结构
import numpy as np from math import sqrt import torch from torch import nn class Self_Attention(nn.Module): # input: batch size * seq_len * input_dim # q k v: (batch size, input_dim, dim k) def __init__(self, input_dim, dim_k, dim_v): super(Self_attention, self).__init__: self.q = nn.Linear(input_dim, dim_k) self.k = nn.Linear(input_dim, dim_k) self.v = nn.Linear(input_dim, dim_v) self.__norm_fact = 1 / sqrt(dim_k) def forward(self, x): Q = self.q(x) # Q: (batch_size, seq_len, dim_k) K = self.k(x) # K: (batch_size, seq_len, dim_k) V = self.v(x) # V: (batch_size, seq_len, dim_v) attn_scores = torch.matmul(Q, K.permute(0, 2, 1)) # Q·K^T attn_scores = attn_scores * self.__norm_fact # 缩放 attn = nn.Softmax(dim=-1)(attn_scores) # Softmax归一化 output = torch.bmm(attn, v) return output X = torch.randn(4, 3, 2) # 输入维度:(batch=4, seq=3, input_dim=2) print(X) self_attn = Self_Attention(2, 4, 5) # input_dim:2 k_dim: 4 v_dim: 5 res = self_attn(X) print(res.shape) # [4, 3, 5] -
self-MHA代码
from math import sqrt import torch import torch.nn as nn from torch import permute class Self_Attention_Multi_Head(nn.Module): # 输入张量维度 input: (batch_size , seq_len , input_dim) def __init__(self, input_dim, dim_k, dim_v, nums_head): super(Self_Attention_Multi_Head, self).__init__() # q k v: (batch_size , input_dim , dim_k) self.q = nn.Linear(input_dim, dim_k) # Q线性变换层 self.k = nn.Linear(input_dim, dim_k) # K线性变换层 self.v = nn.Linear(input_dim, dim_v) # V线性变换层 self.nums_head = nums_head # 头数 self.dim_k = dim_k # 总键维度 self.dim_v = dim_v # 总值维度 self._norm_fact = 1 / sqrt(dim_k) # 缩放因子 # x: (batch_size, seq_len, input_dim) def forward(self, x): # Q: (batch_size, seq_len, dim_k) # reshape:(num_heads, batch_size, seq_leng, head_dim) Q = self.q(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head) K = self.k(x).reshape(-1, x.shape[0], x.shape[1], self.dim_k // self.nums_head) V = self.v(x).reshape(-1, x.shape[0], x.shape[1], self.dim_v // self.nums_head) # batch_size, num_heads, seq_len, seq_len # Q * K.T(): batch_size * num_heads * seq_len * seq_len attn_scores = nn.Softmax(dim=-1)(torch.matmul(Q, K.permute(0, 1, 3, 2))) output = torch.matmul(attn_scores, V).reshape(x.shape[0], x.shape[1], -1) # Q * K.T() * V: (batch_size * seq_len * dim_v) return output x = torch.rand(1, 3, 4) print(x) attn = Self_Attention_Multi_Head(input_dim=4, dim_k=4, dim_v=4, nums_head=2) y = attn(x) -
详述FFN,FFN和mlp区别
-
手撕mlp
import numpy as np class Relu: def forward(self, x): self.x = x return np.maximum(0, x) def backward(self, grad_output, lr):# 这里的lr没有用到,但是为了保持参数接口的一致性,还是保留了 return grad_output * (self.x > 0) # relu函数的一阶导数,大于0部分为1,小于0部分为0 class LinearLayer: def __init__(self, input_c, output_c): # y = x @ w + b # self.w = np.random.rand(input_c, output_c) self.w = np.random.rand(input_c, output_c) * 0.001 # 这里乘上0.001是为了防止结果太大,梯度爆炸 self.b = np.zeros(output_c) def forward(self, x): self.x = x # 这里保存输入,为了后续在反向传播中计算梯度 # y = x @ w + b return np.dot(x, self.w) + self.b def backward(self, grad_output, lr): # linear层的梯度计算,涉及三个参数,x,w,b,为 dx, dw, db # 其中,dw和db是为了更新w和b # dx是为了计算下一层的梯度,链式法则 # y = x @ w + b # dl / dx = dl / dy * dy / dx = grad_output * w # 这里要注意矩阵的维度要对齐 grad_input = np.dot(grad_output, self.w.T) # dl / dw = dl / dy * dy / dw = grad_output * x # 这里要注意矩阵的维度要对齐 w_grad = np.dot(self.x.T, grad_output) b_grad = np.sum(grad_output, axis=0) # 更新w和b的参数 self.w -= lr * w_grad self.b -= lr * b_grad return grad_input class MLP: def __init__(self, input_c, hidden_c, output_c, layers_num): self.layers = [] # 初始化网络第一层 self.layers.append(LinearLayer(input_c, hidden_c)) self.layers.append(Relu()) # 初始化网络中间层 for i in range(layers_num - 2): self.layers.append(LinearLayer(hidden_c, hidden_c)) self.layers.append(Relu()) # 初始化网络最后一层,注意,最后一层没有relu激活函数 self.layers.append(LinearLayer(hidden_c, output_c)) def forward(self, x): res = x for layer in self.layers: res = layer.forward(res) return res def backward(self, grad_output, lr): grad = grad_output # 倒序遍历每一层,反向传播,计算每一层梯度 # for layer in reversed(self.layers): for layer in self.layers[::-1]: grad = layer.backward(grad, lr) return grad if __name__ == '__main__': input_data = np.random.rand(2, 8) input_c = 8 hidden_c = 16 output_c = 3 layers = 5 target = np.random.rand(2, 3) mlp_model = MLP(input_c, hidden_c, output_c, layers) # print(mlp_model.layers) for i in range(10): print(f'[Epoch: {i} / 100]', end=' ') res = mlp_model.forward(input_data) # 计算损失loss,这里使用mse,均方误差函数 loss = ((res - target) ** 2).mean() # 损失对于最后一层输出res的梯度 loss_grad = 2 * (res - target) # 反向传播,计算每一层梯度 mlp_model.backward(loss_grad, lr=0.1) print(f'[loss: {loss}]') -
为什么排序效果比召回更好?
-
Learning to rank是什么
(上面两道是搜广推的题目) -
过拟合和欠拟合的定义,怎么解决
问题 定义 表现
欠拟合 模型过于简单,无法捕捉数据中的基本规律(高偏差)。 训练集和测试集上表现均差。
过拟合 模型过于复杂,过度拟合训练数据中的噪声或细节(高方差)。 训练集表现好,测试集表现差(泛化能力弱)。 -
L1L2正则化分别是什么,公式,使用场景,两者数学方面的区别
-
L1正则化:权重系数的绝对值之和
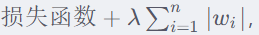
-
L2正则化:权重系数的平方和
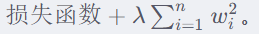
-
使用场景:
L1正则化常用于特征选择,因为它可以将不重要的特征的系数压缩到0。因此,L1正则化适用于特征数量多且需要进行特征选择的场景。
L2正则化常用于防止模型过拟合,它适用于特征数量较少且需要保持模型稳定性的场景。 -
两者数学方面的区别
L1正则化在参数空间中形成了一个菱形的可行域,而L2正则化在参数空间中形成了一个圆形的可行域。
L1正则化可以产生稀疏的权重矩阵,即许多权重会变为0,而L2正则化则会使得权重值更趋于较小的值,但不会变为0。
L1正则化适用于特征选择,而L2正则化适用于防止模型过拟合。
-
-
dropout在训练和推理阶段有什么区别?训练和测试的阶段一样吗,怎么平衡训练测试时的差异
- dropout作用
- 防止过拟合:通过在训练过程中随机“丢弃”一部分神经元(即将这些神经元的输出置为零),Dropout减少了神经元之间的共适应性,迫使网络学习到更加鲁棒和泛化能力强的特征。
- 集成学习效果:每次训练迭代中,Dropout相当于训练了一个不同的子网络。最终模型的预测可以看作是这些子网络的集成,从而提升了模型的整体性能和稳定性。
- 减少神经元共适应性:Dropout迫使每个神经元不依赖于特定的其他神经元,使得网络结构更加健壮,减少了对特定特征的过度依赖。
- 训练测试区别、平衡差异
- 训练阶段:使用 Dropout,随机丢弃一部分神经元的输出,并对剩余神经元的输出进行缩放。
- 测试阶段:不使用 Dropout,保留所有神经元的输出,不进行缩放。
- dropout作用
-
AUC的定义和计算方式
AUC(Area Under Curve)是ROC曲线(Receiver Operating Characteristic Curve)下的面积,用于衡量二分类模型的性能。ROC曲线以真阳性率(TPR)为纵轴,假阳性率(FPR)为横轴,通过不同阈值下的分类结果绘制而成。 -
AUC 的两个物理意义 公式和时间复杂度
物理意义:AUC的物理意义是从测试集中任选一个正样本,再任选一个负样本,模型对正样本预测分值大于负样本的概率 -
随机采样负样本对AUC有什么影响
-
召回时,如果数据集过大,如何提高召回效率?
-
优化器了解多少,展开说说
-
Adam优化器的原理(一阶矩、二阶矩、偏差校正)
-
SGD和Adam对比展开说说
SGD通过在每次迭代中随机选择一个或多个样本(小批量)来计算梯度,然后更新模型参数。它是一种简单且高效的优化算法。
Adam结合了动量(Momentum)和RMSprop优化器的优点。它通过计算梯度的一阶矩(均值)和二阶矩(未中心化的方差)来自适应地调整学习率。 -
MHA的公式 Q K V意义 手撕MHA代码 dk意义

-
MHA的时间复杂度


-
LoRA微调原理解释 为什么省显存

省显存:- 参数量少
- 冻结初始权重,只训练新增权重
- 存储开销小
- 模块化设计
-
为什么现在大模型都是decoder only而不是encoder-decoder
架构简单高效:移除编码器,简化模型结构,减少计算开销。
预训练优势:自回归预训练(预测下一个词)更简单,数据需求少。
任务灵活性:更适合对话、文本生成等动态任务。
性能与扩展性:在大规模预训练和多任务适应性上表现更好。
推理效率:生成新标记时无需重新计算整个输入,推理更快。 -
scaling law了解多少?哪一项提升对模型的帮助最大?公式了解多少?
-
Kmeans损失函数,每个簇的中心点怎么选。推导一下Kmeans参数()M 算 法)


-
交叉熵损失函数 、KL散度交叉熵和KL使用场景、两者区别联系

区别:
交叉熵损失函数是KL散度的一个特例,当真实分布是one-hot编码时,KL散度就变成了交叉熵损失函数。
交叉熵损失函数是模型训练中常用的损失函数,而KL散度更多地用于衡量概率分布之间的差异。
联系:
交叉熵损失函数和KL散度都是衡量概率分布之间差异的方法,它们在数学上是等价的,只是在不同的场景下使用不同的名称。 -
还用过什么损失(MAE等), 为什么分类不用MAE
在分类任务中,真实标签是离散的(如0或1),而模型的输出是连续的概率值(如0.7、0.3等)。MAE在这种情况下无法有效衡量模型的性能,因为它直接计算离散值和连续值之间的绝对误差。 -
交叉熵,求导过程























 3万+
3万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








