三体运动——基于MWORKS.Sysplorer研究初值对混沌系统数值求解的影响

近期，根据作家刘慈欣同名科幻小说改编的电视剧《三体》热播，宏大的内容叙事、高燃硬核的科幻设定、危险幽深的宇宙观念......无一不令人热血澎湃，作为高中熬夜读小说的三体粉，笔者自然不会错过。

“三体”名称来源于“三体问题”，剧中借怪才数学家魏成之口对这一概念进行了解释，笔者高中时期对书中场景的漫天想象也随着剧中魏成的描述逐渐清晰。

剧照：魏成解释“三体问题”

本期，我们就从科学的角度了解一下三体问题，并基于MWORKS.Sysplorer对三体问题展开一些仿真工作。

1  三体问题

“什么是三体问题，科学家又是如何围绕这一课题展开研究的？”这是一个有着四百年历史的数学问题，其根源在于模拟“日-地-月”系统的失败尝试。1885年，学数学出身的瑞典国王奥斯卡二世赞助了一场有奖数学竞赛，竞赛的题目是4个数学难题，其中之一便是多体问题——求解太阳系的运动问题。这一难题从牛顿时代提出直到竞赛发布之时，在学术界始终无人能攻克。

实际上这是一个N体问题，即在三维空间中给定N个质点，如果在质点之间只有万有引力的作用，在给定初始位置和速度的条件下，它们会怎样运动。法国科学家亨利·庞加莱将对问题进行了简化，只考虑三个星体，这就是著名的“三体问题”。

2  混沌系统

1887年，德国数学家Heinrich Bruns指出，寻找三体问题的通解注定是做无用功，只在特定条件下成立的特解才可能存在。依据这一思路，科学家们重新审视“三体问题”，找到了三类特解：拉格朗日点特解（提出者：欧拉和拉格朗日），布鲁克-赫农族特解（提出者：罗杰·布鲁克和米歇尔·赫农），以及“8”字形族特解（提出者：克里斯·摩尔）。2013年，贝尔格莱德大学的Milovan Šuvakov和Veljko Dmitrašinović两位科学家，利用计算机模拟从现有的特解出发，调整初始条件直到新类型的轨道能具体化，将特解总数增加到16类。

科学家们研究后发现，在给定的初始条件下，当时间趋于无穷时，几乎无法预测三体轨道的最终命运。这种对于轨道的长时间行为的不确定性，目前学界称之为混沌(chaos)现象。

由于三体问题没有显示解，即无法根据给定的时刻确定状态，因此科学家寻找特解也是基于数值算法，即根据当前时刻的状态递推下一时刻的状态。在这个递推过程中，由于计算机计算方式存在误差，因此递推的时间越长，误差会越大，可能会导致结果完全偏离。也就是说，初始值的细微差别可能会使得混沌系统数值求解产生完全不同的结果。

3  三体系统建模与仿真

同元软控自主研发的系统建模仿真环境MWORKS.Sysplorer具有完整的系统建模、编译分析、求解计算、后处理等功能，且编译求解内核达到国际先进水平。我们基于MWORKS.Sysplorer平台，利用天体引力场模型库快速建立三体运动模型，研究初值对混沌系统数值求解的影响。

首先，建立三体运动模型，有以下假设：

• 不考虑天体形状，将天体均简化为质点；

• 考虑引力场为质点引力场；

天体引力场模型库提供质点引力场、球谐引力场、多面体引力场模型，在此选用质点引力场模型，计算原理即为万有引力公式：

式中：

为天体受到的万有引力矢量；

为万有引力常数；

为中心天体质量；

为第二天体质量；

为第二天体相对中心天体的相对位置矢量；

为两天体中心距离；

根据三体之间的两两相互间作用力构建三体系统模型，如图1所示。

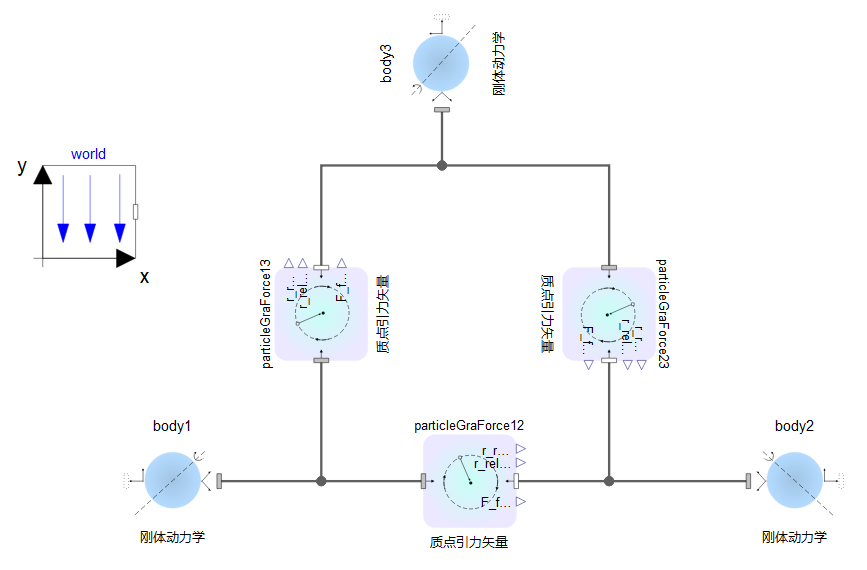
图1 三体系统模型

通过设置三个天体的质量、惯性系下初始位置、惯性系下初始速度，进行仿真，分析三个天体的运动轨迹。

与贝尔格莱德大学的Milovan Šuvakov和Veljko Dmitrašinović两位科学家研究路线相似，首先我们考虑一个特解情况，即三个天体质量相等、在直线上对称分布。

《三体》剧照

仿真的三个天体运行轨迹如图2所示，三个天体的运行轨迹形成首尾相连的“8”字形。

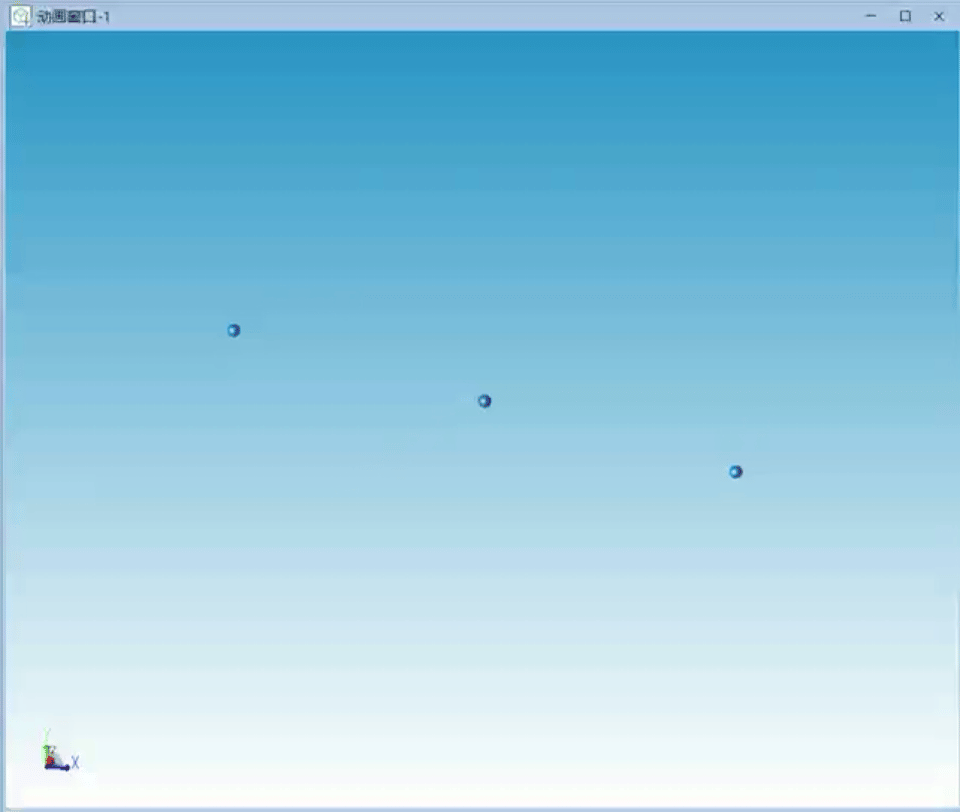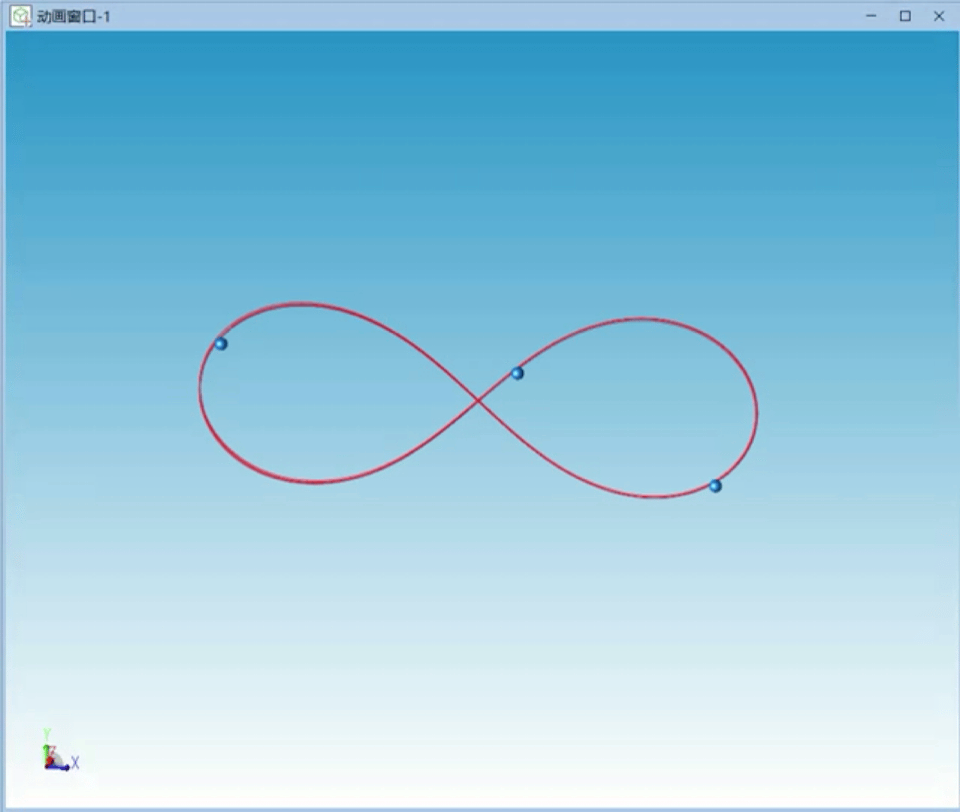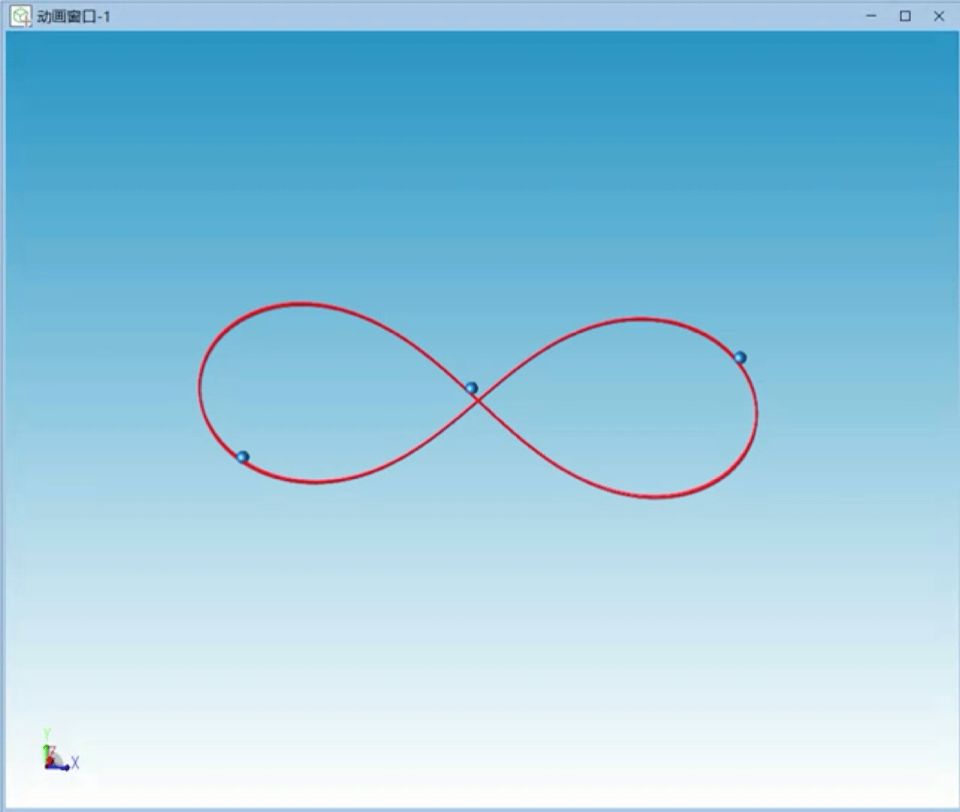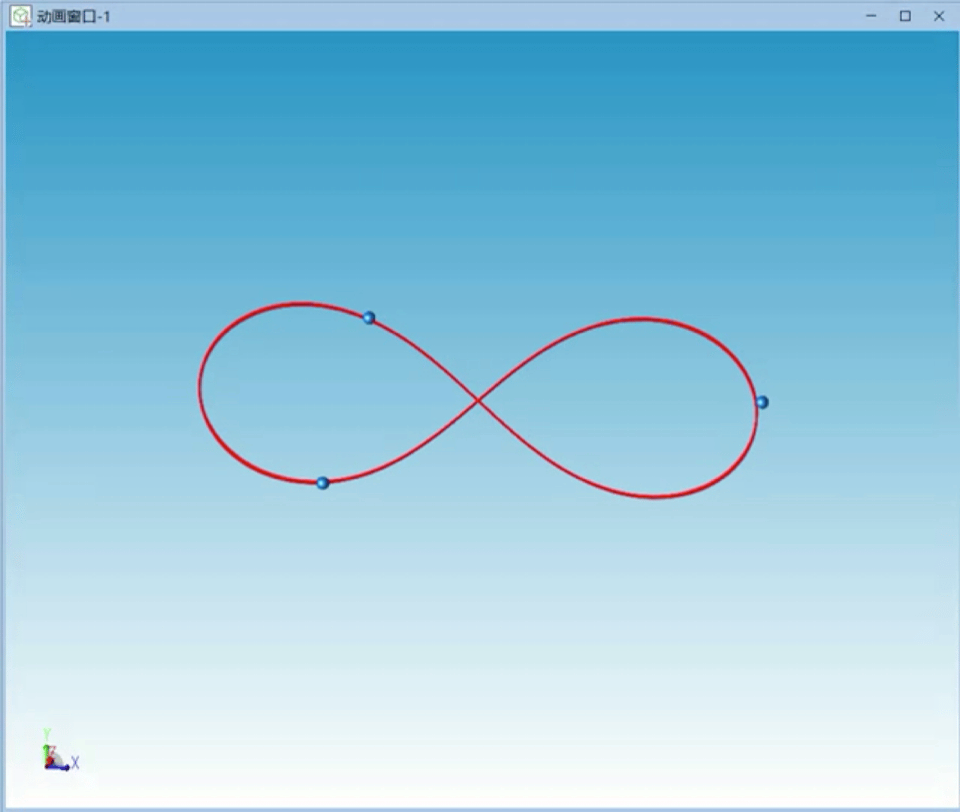
图2 8字形特解

我们考虑另一个特解情况，即三个天体质量相等、在空间中成三角形对称分布，仿真的三个天体运行轨迹如图3所示，三个天体运行轨迹接近一个圆。

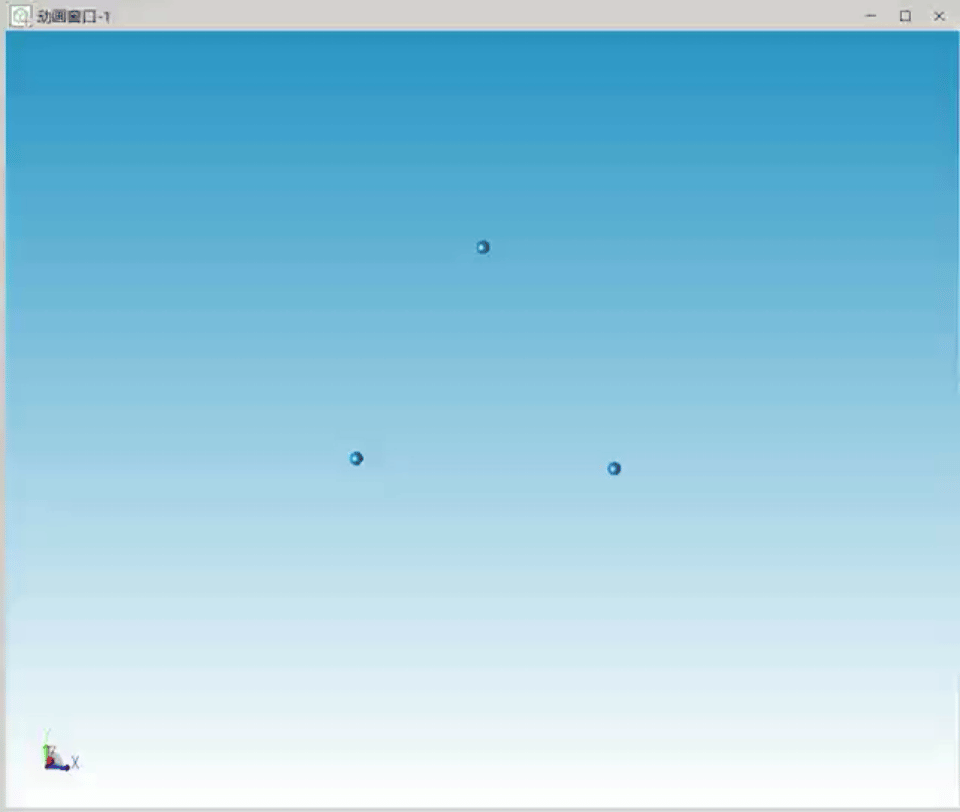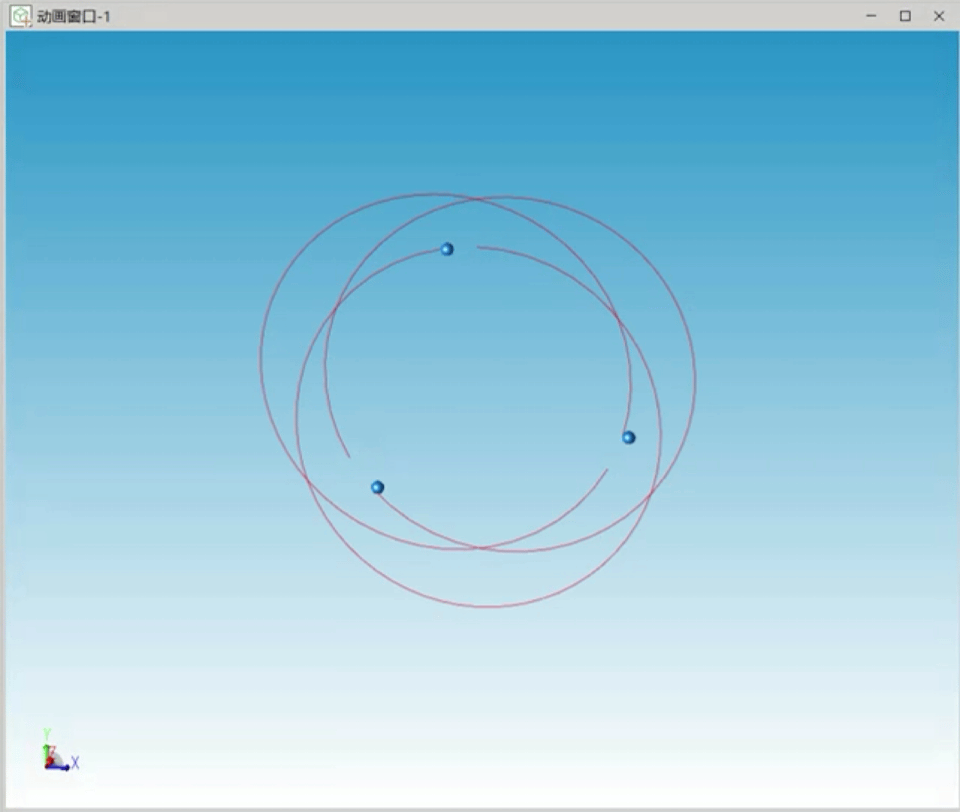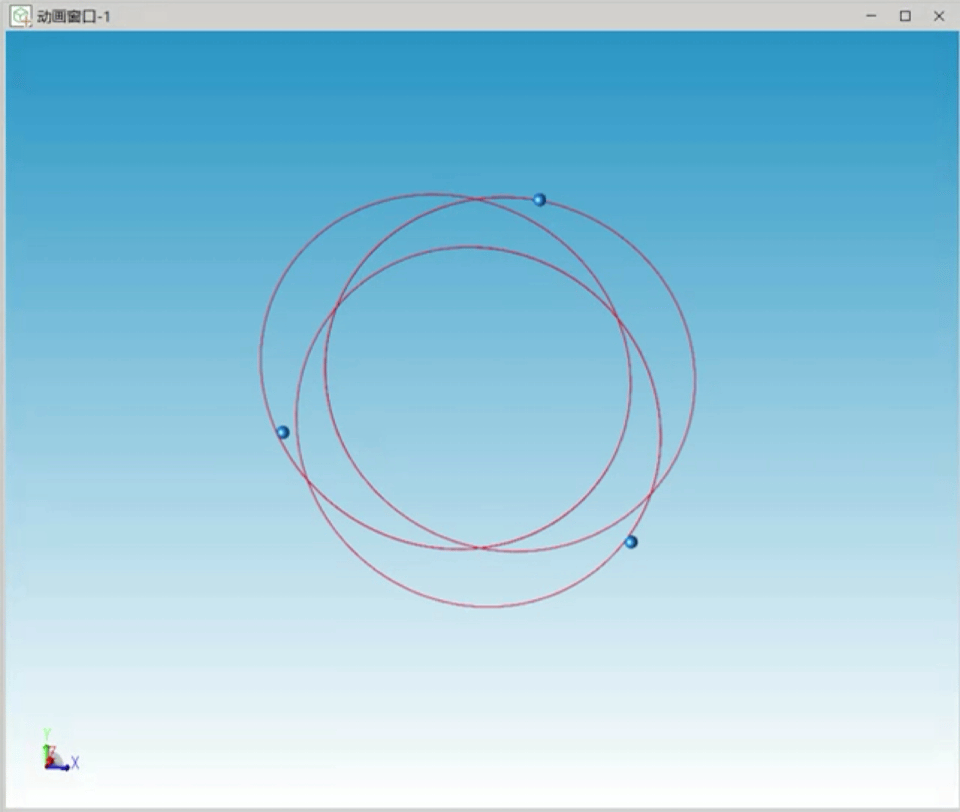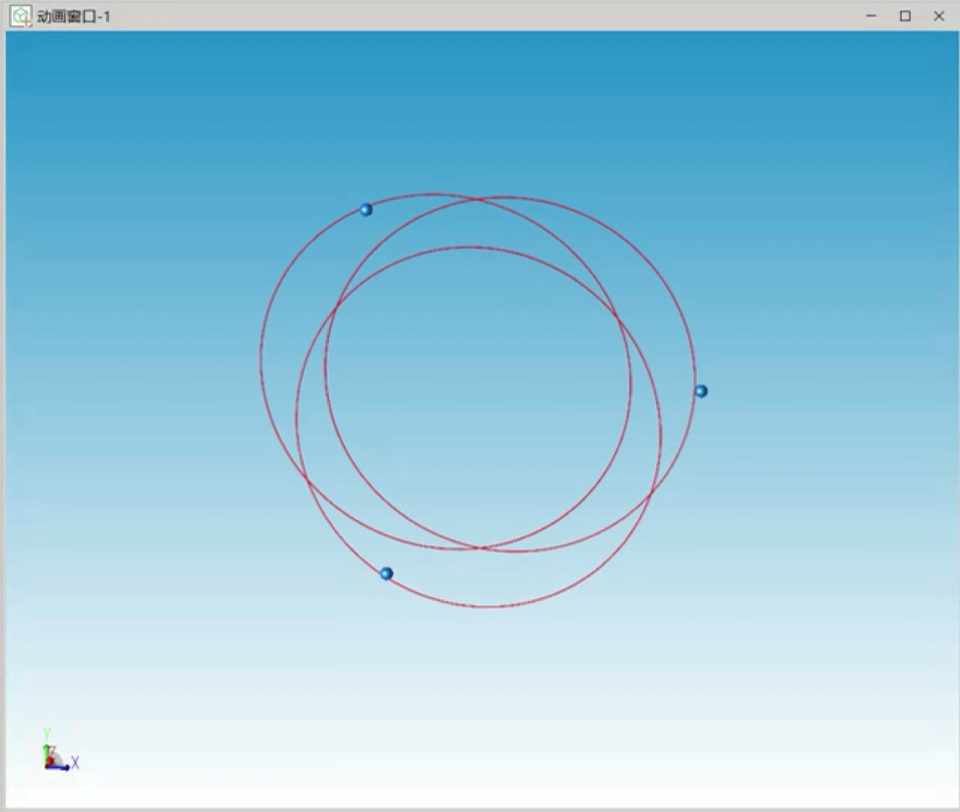
图3 三角形特解

其他初始条件不变的情况下，我们增大三个天体的初始惯性系速度，系统仍在较长时间内稳定，仿真的三个天体运行轨迹如图4所示，三个天体运行轨迹形成椭圆。

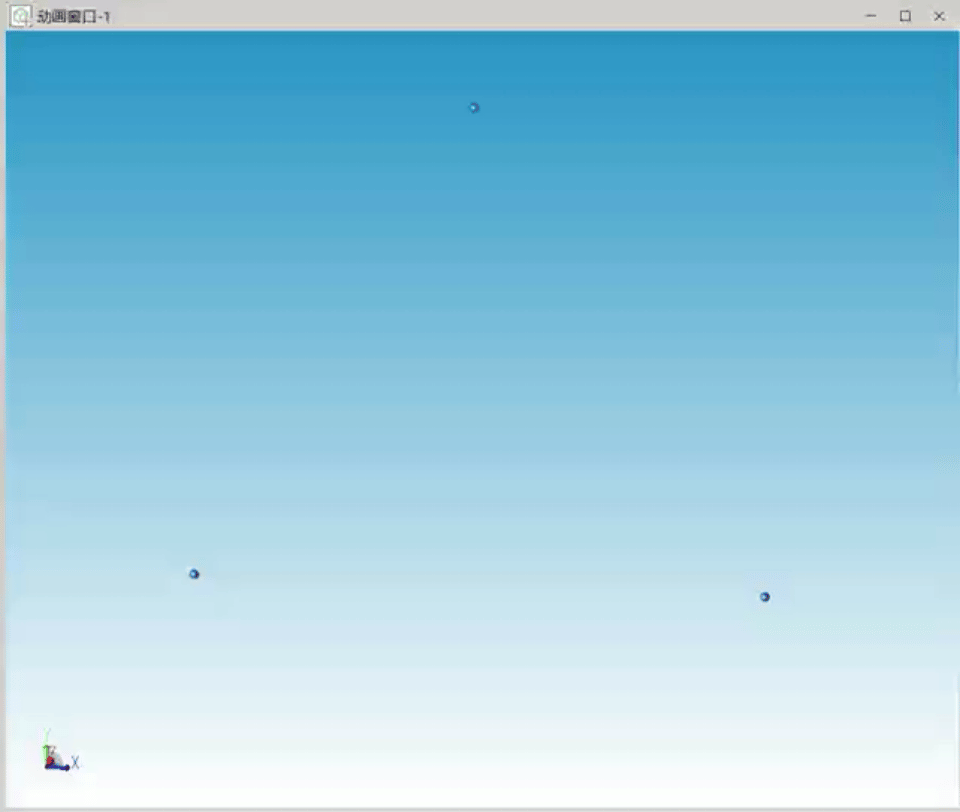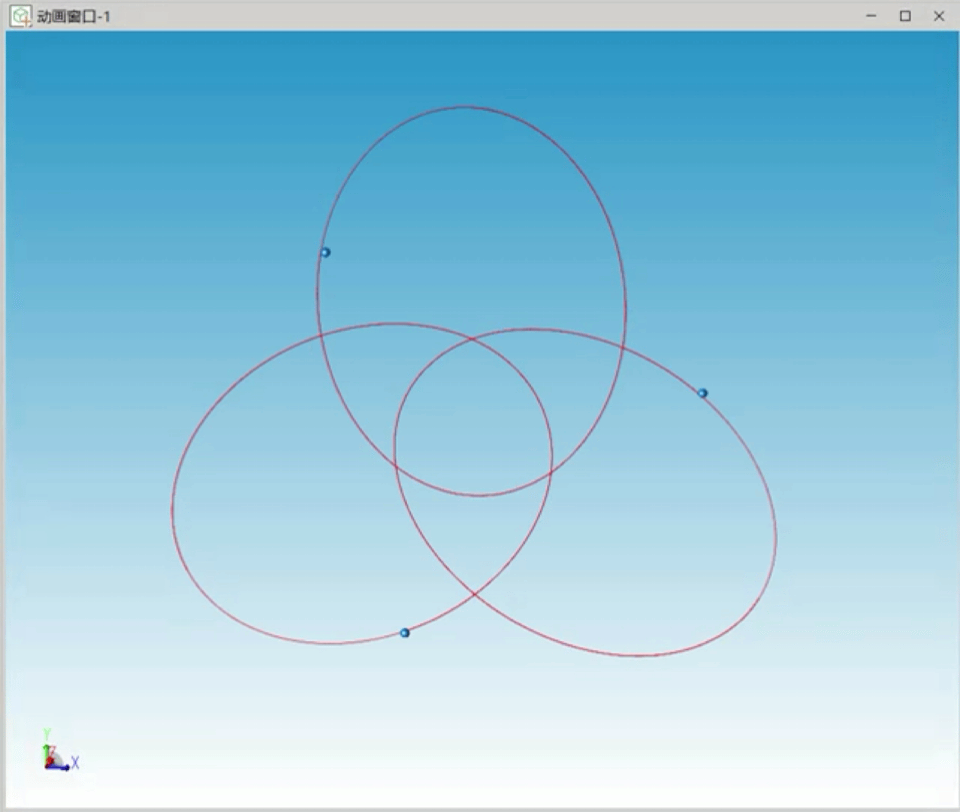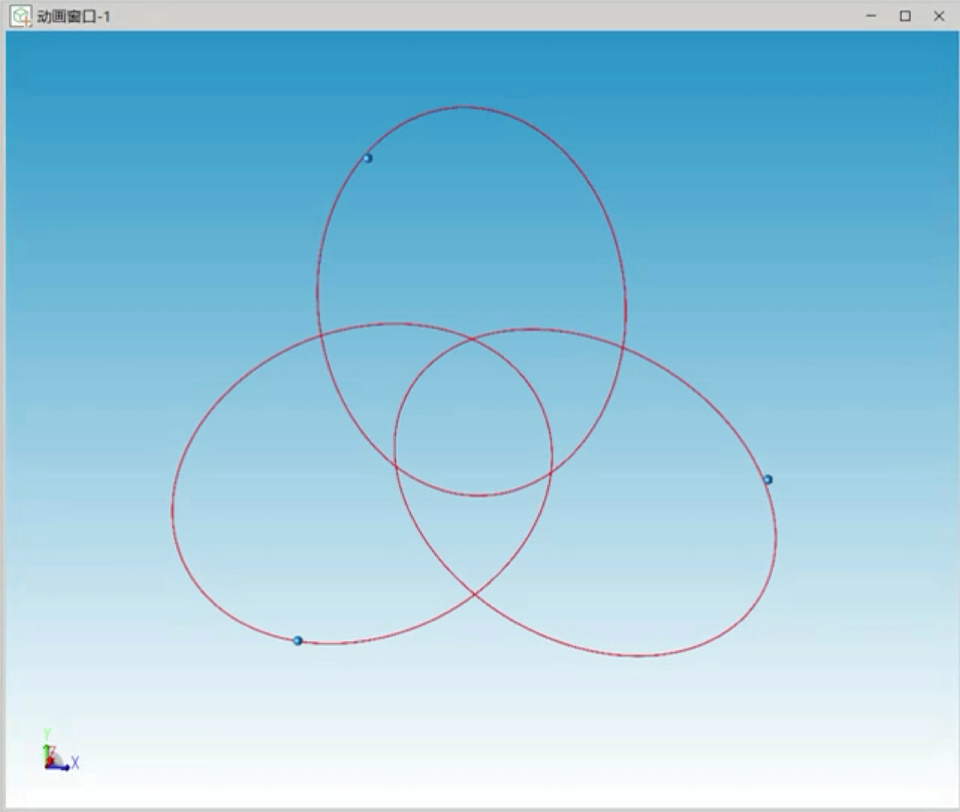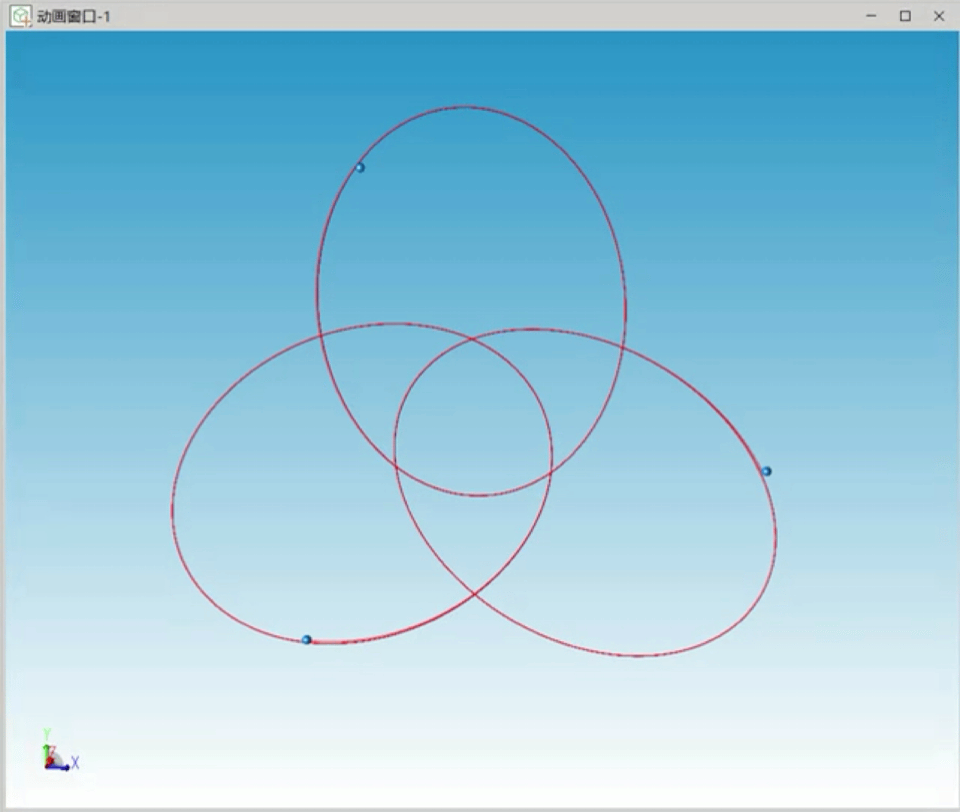
图4 三角形特解

我们增大三个天体的质量差，设置惯性系下初始速度，经过反复尝试稳定的三个天体运行轨迹如图5所示。

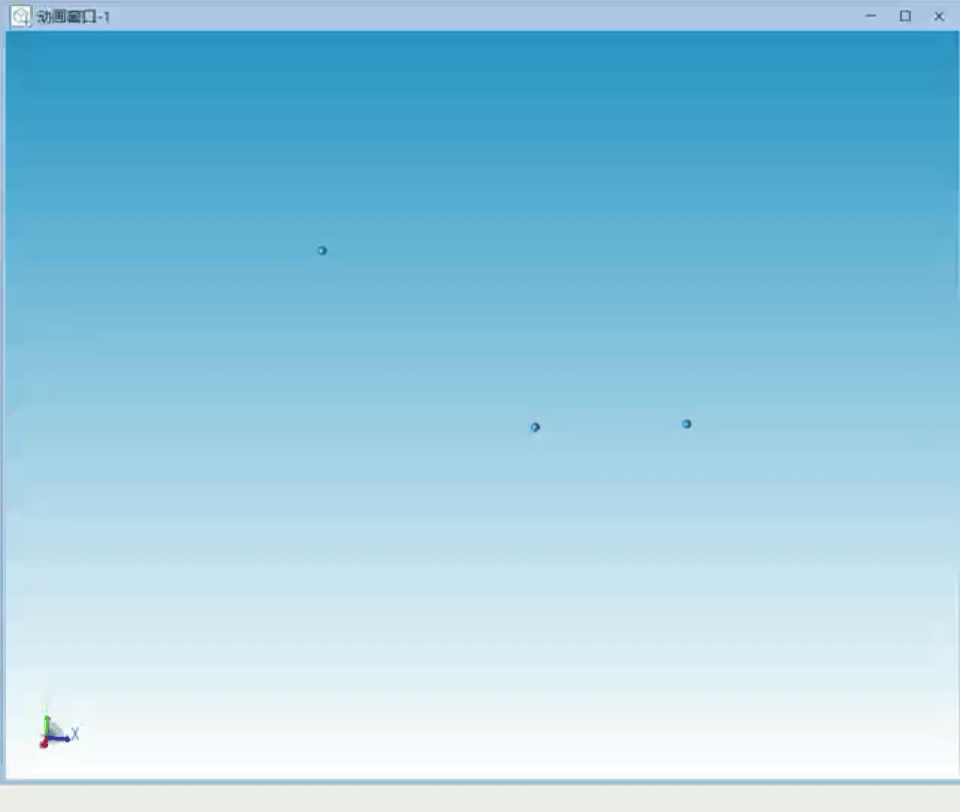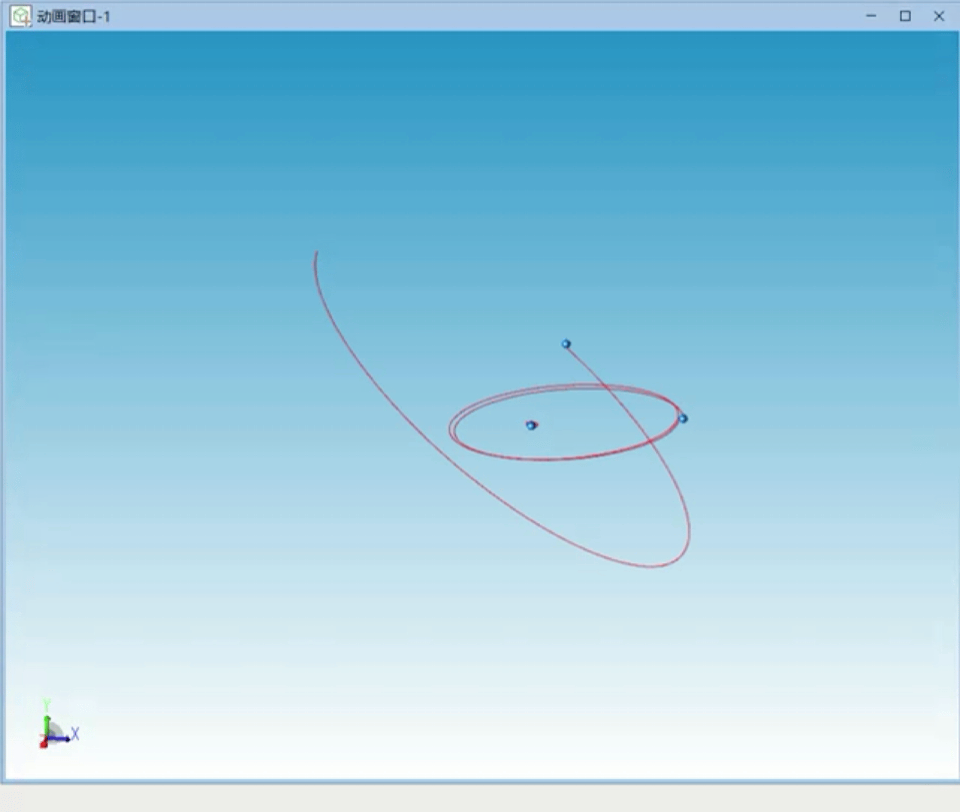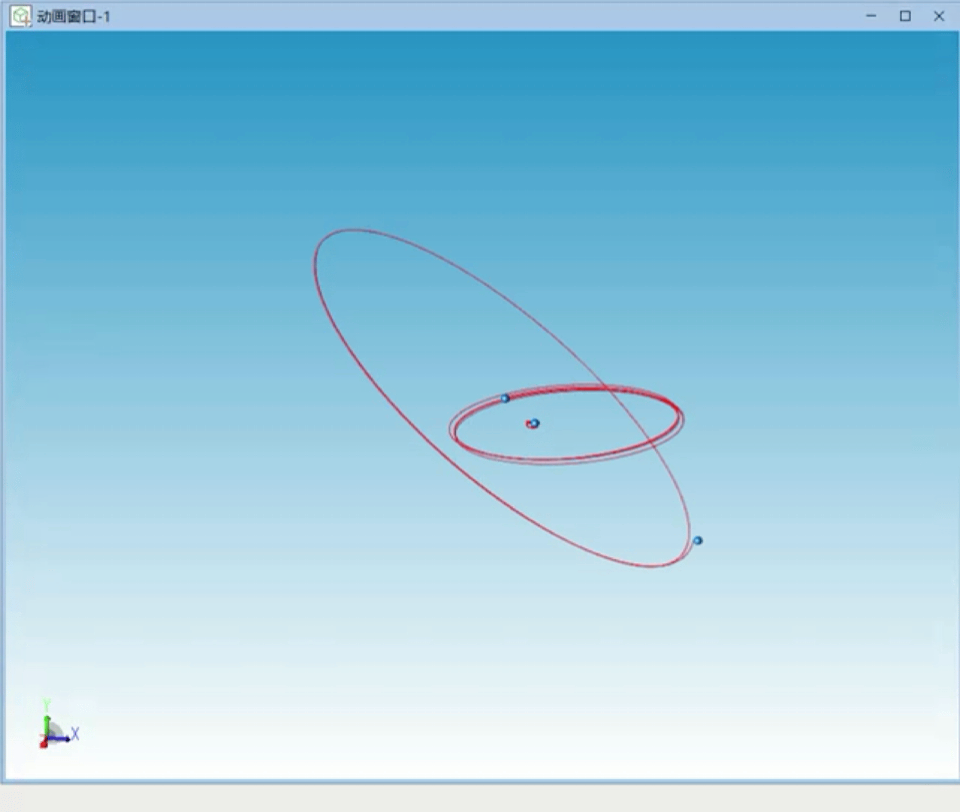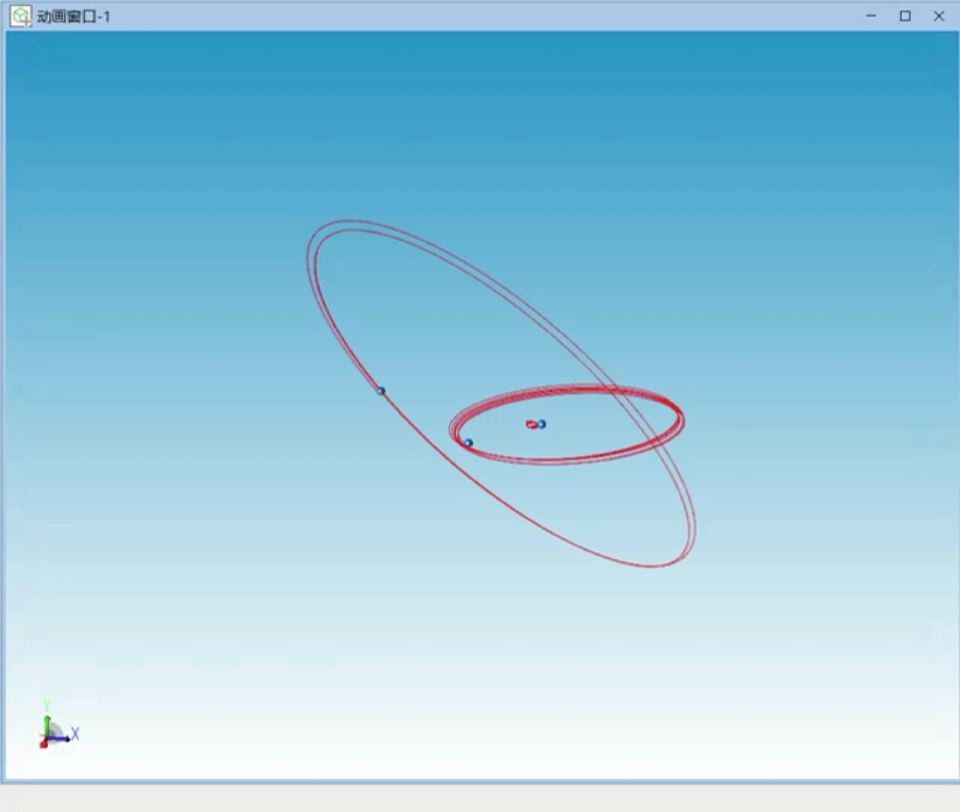
图5 单恒星双行星特解

继续增大三个天体的质量差，设置初始速度，模拟“日-地-月”系统，经过反复尝试稳定的运行曲线三个天体运行轨迹如图6所示。

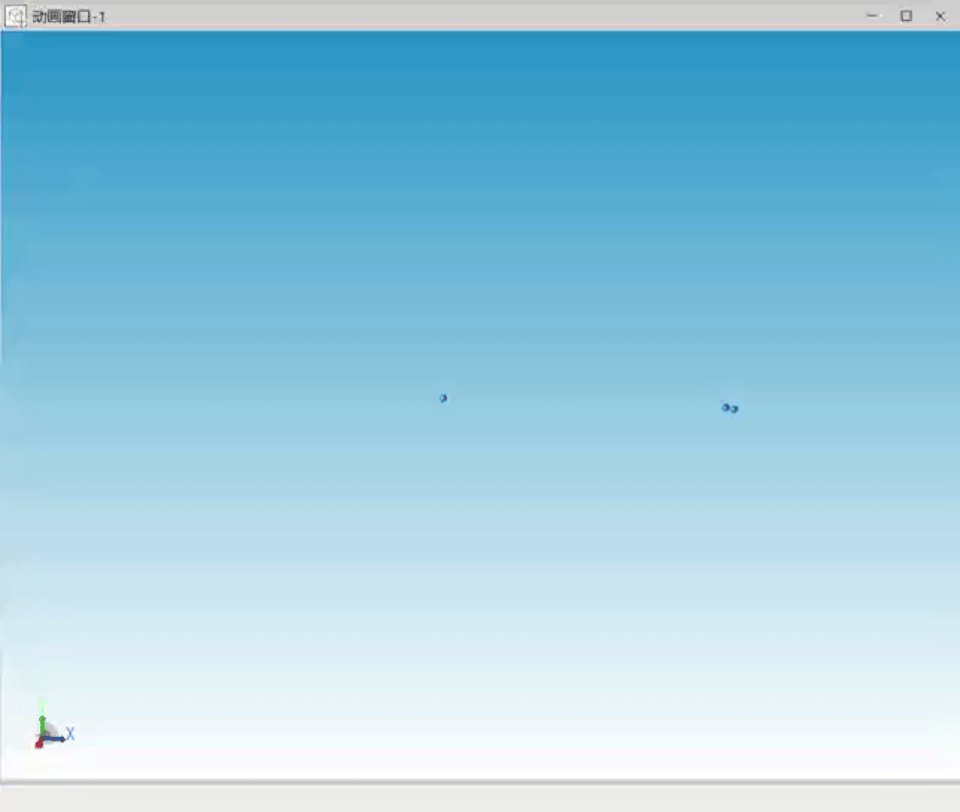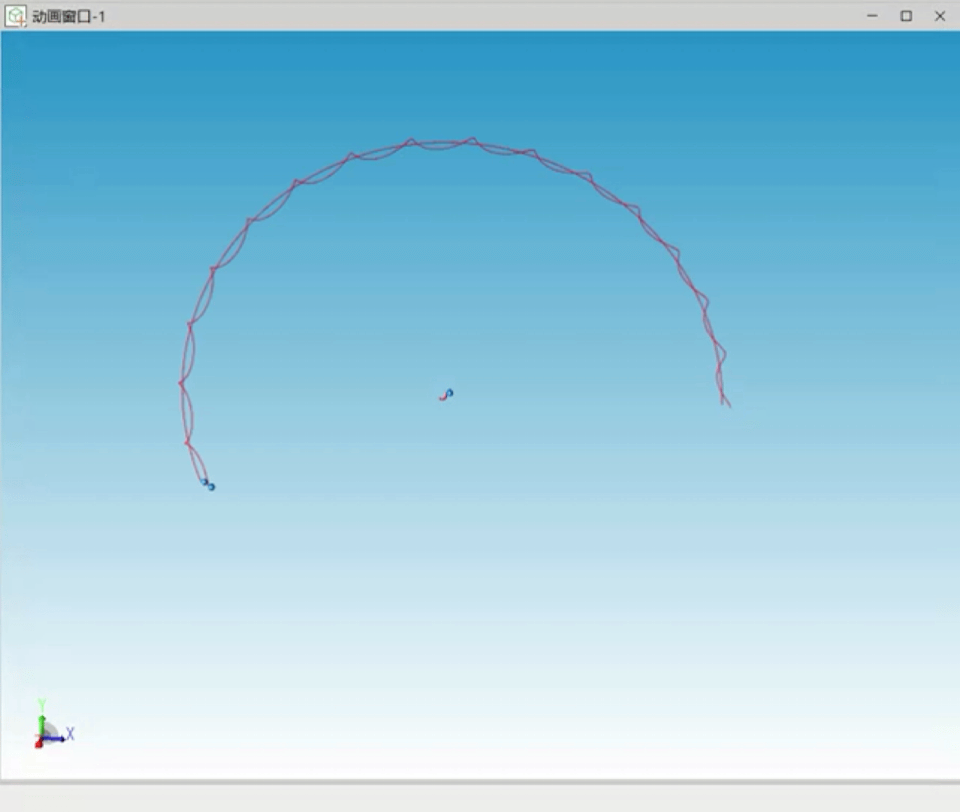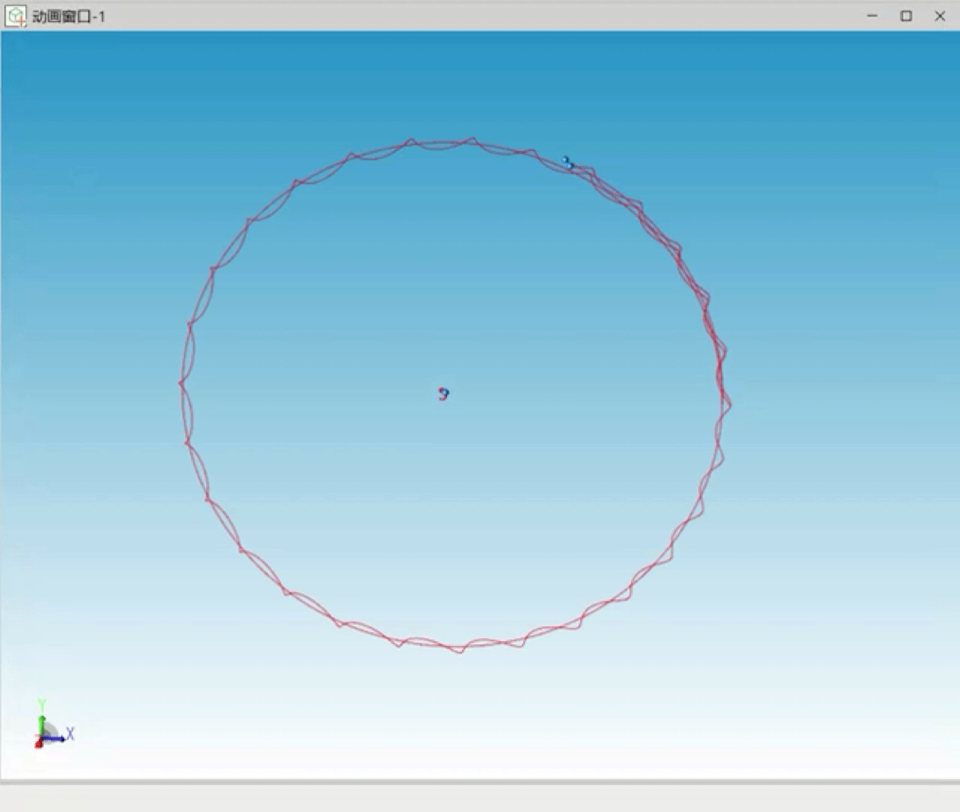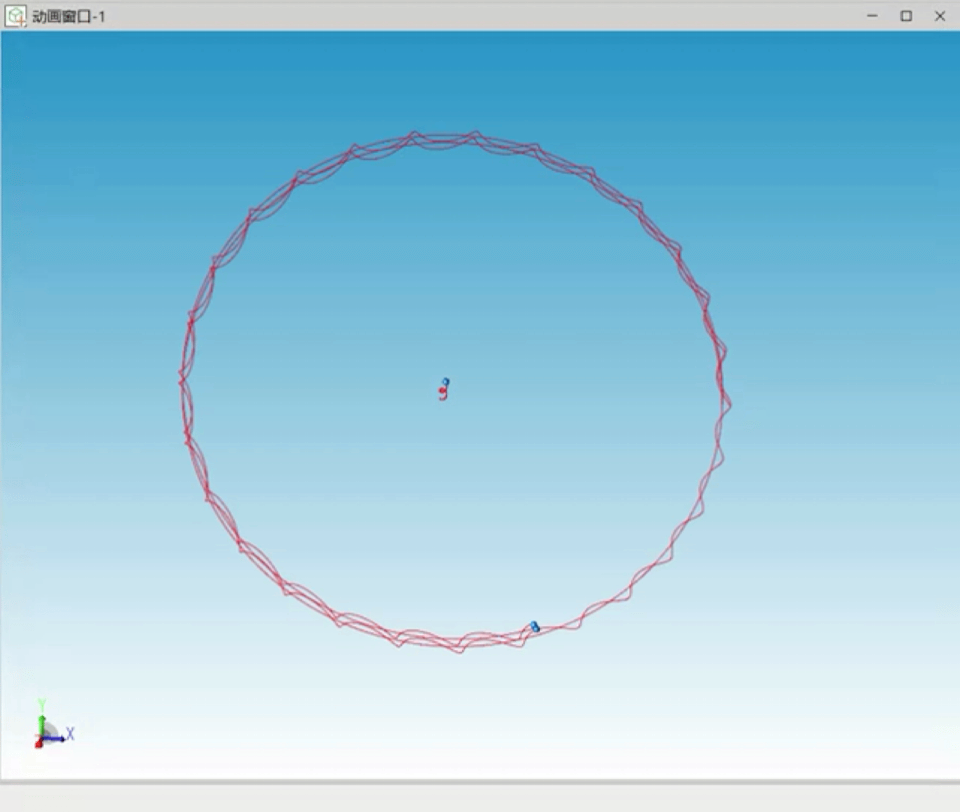
图6 日地月特解

经过仿真过程中的不断调试，笔者对三体问题的混沌性及计算机数值求解时初始值的重要性有了更深刻的认识。以下为调试过程中出现的多种三体不稳定状态曲线：

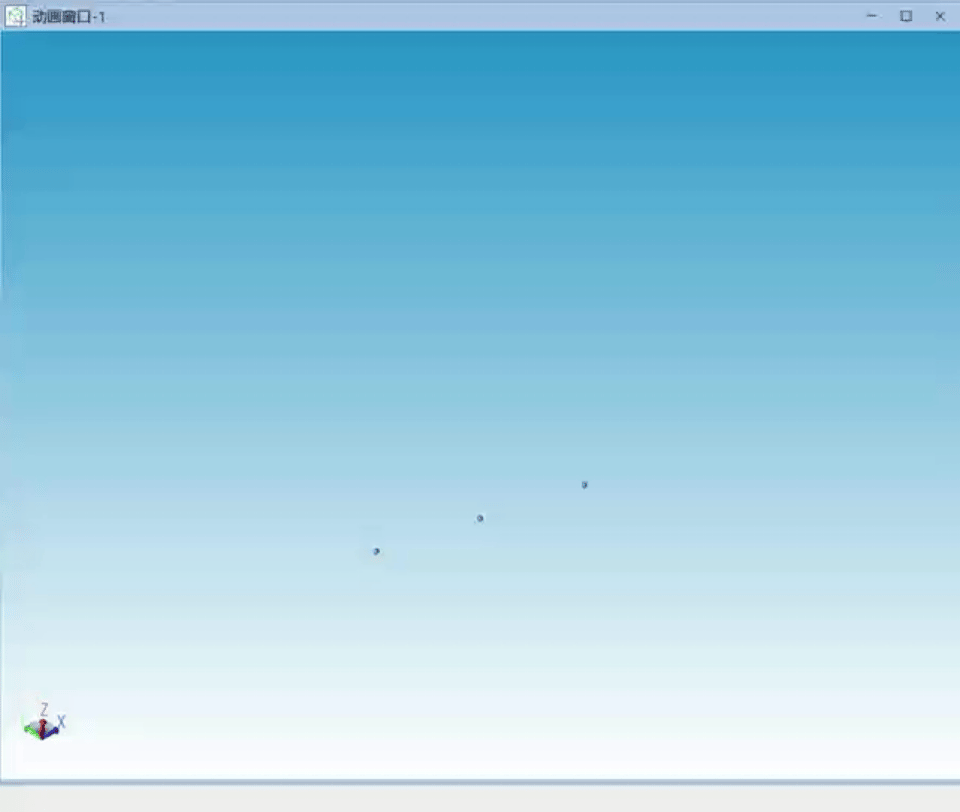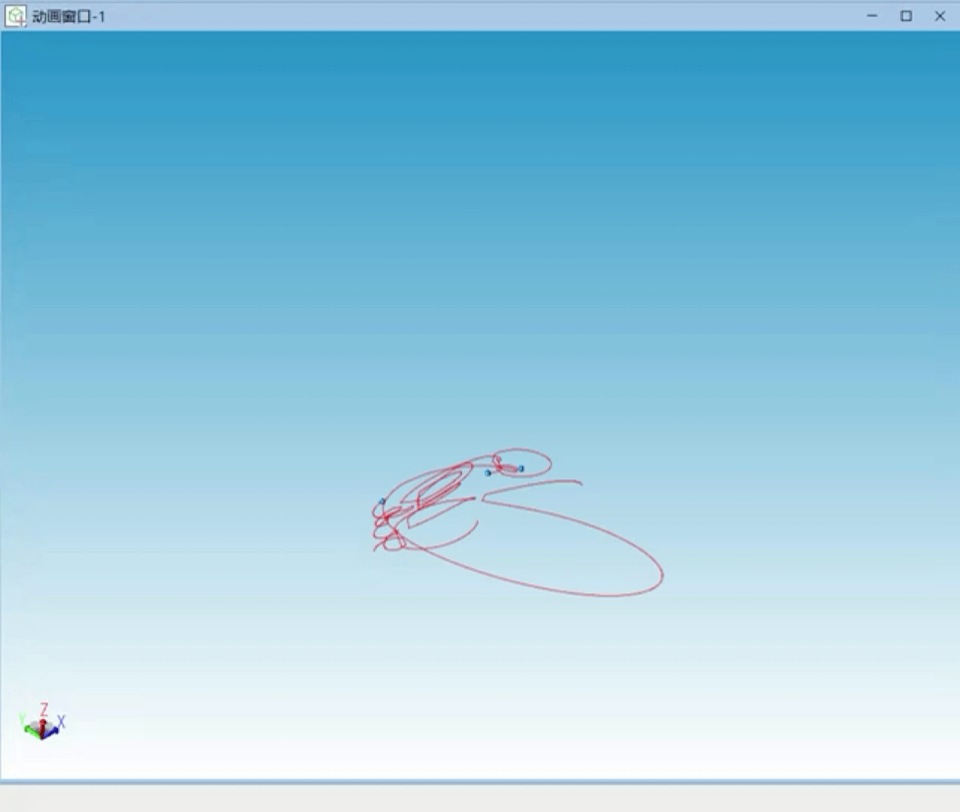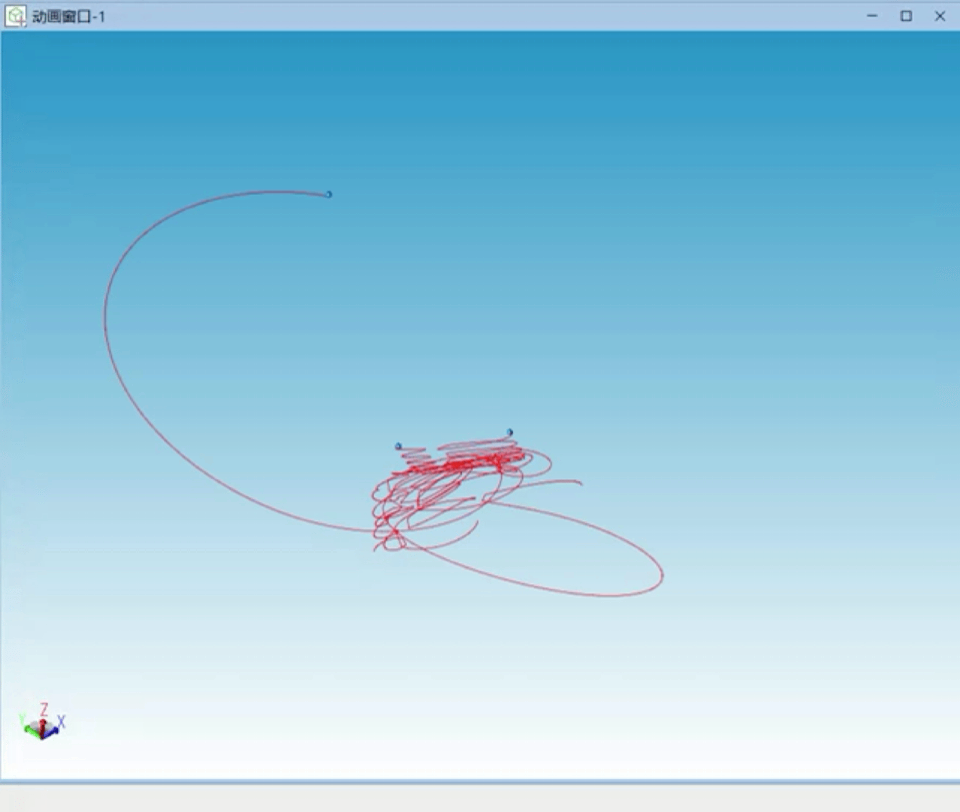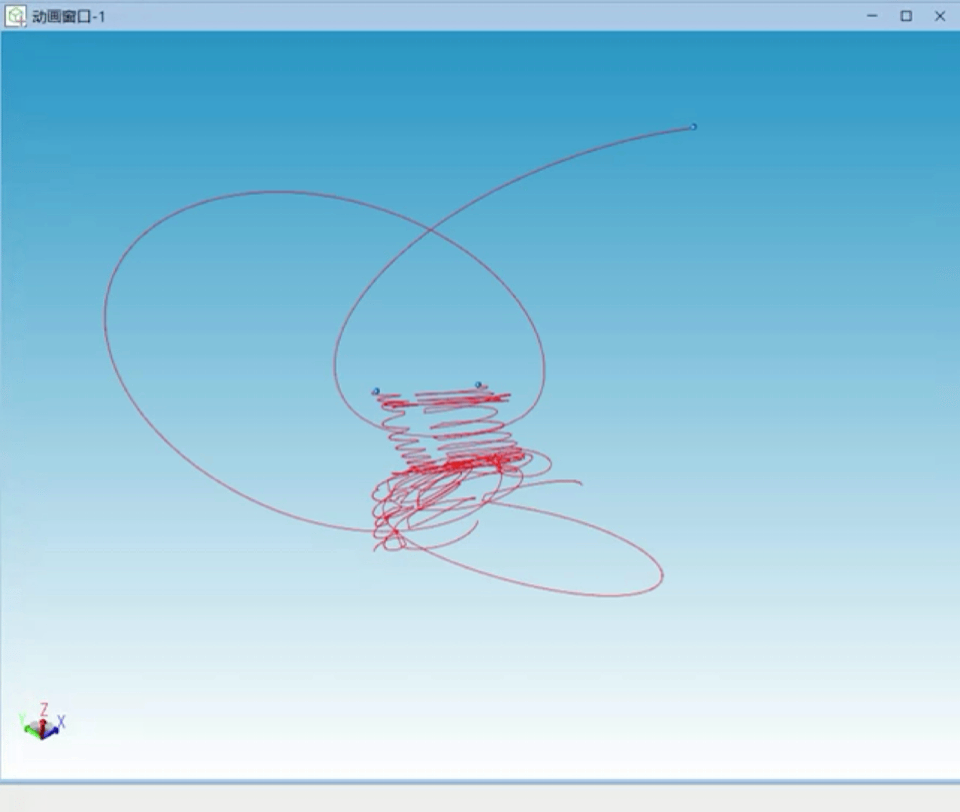
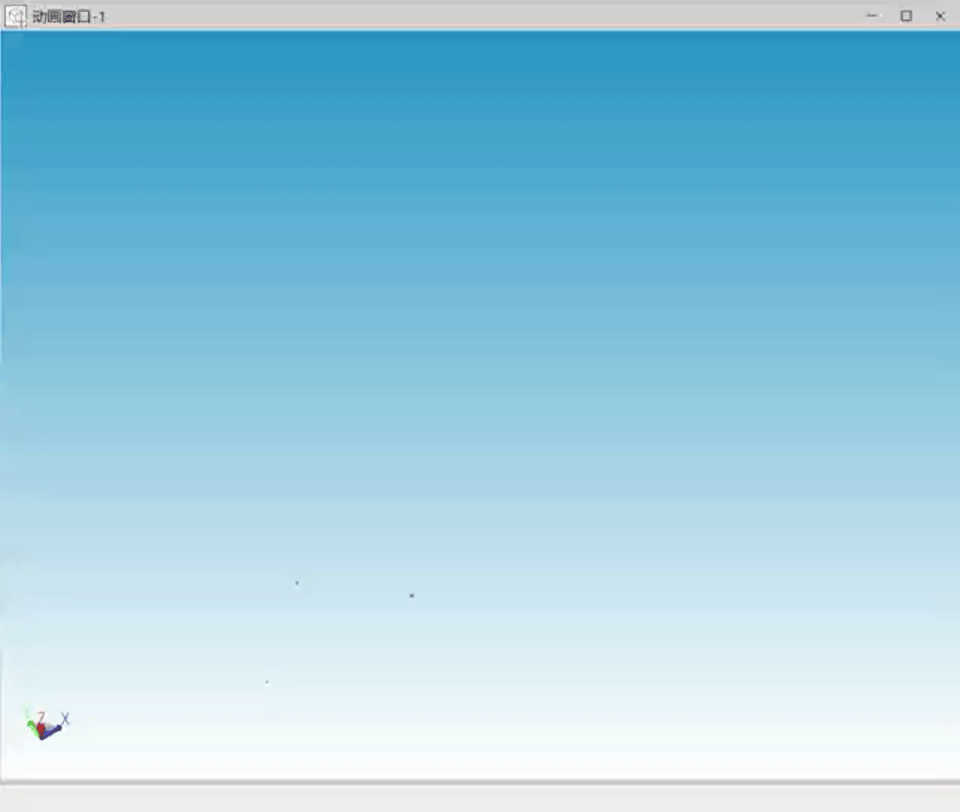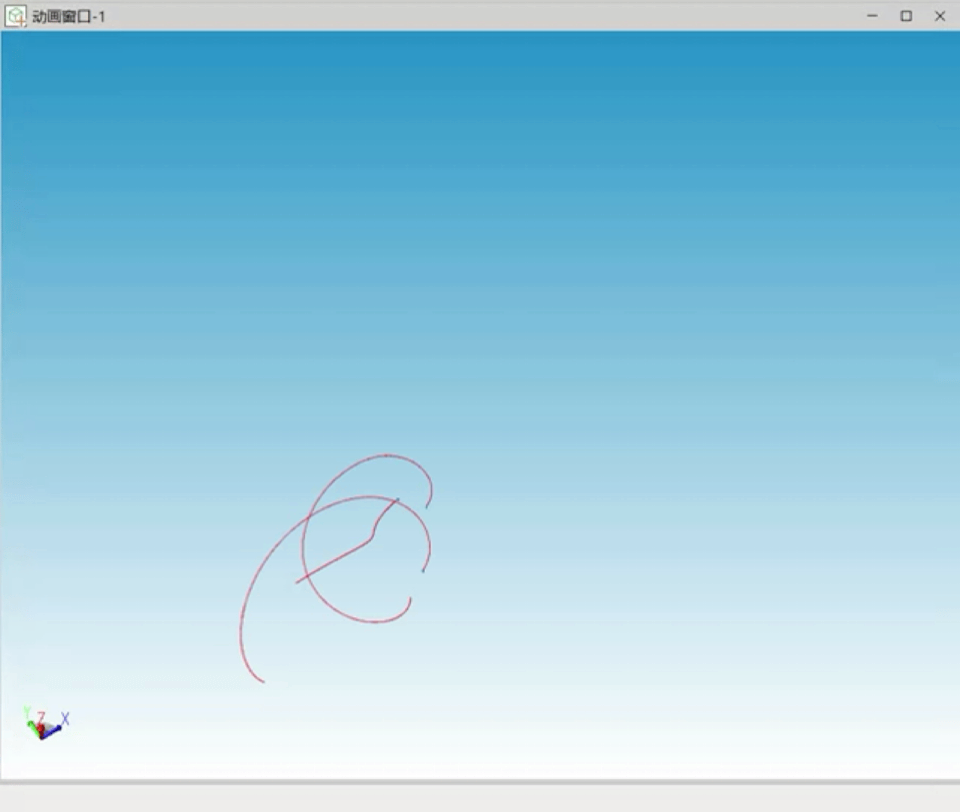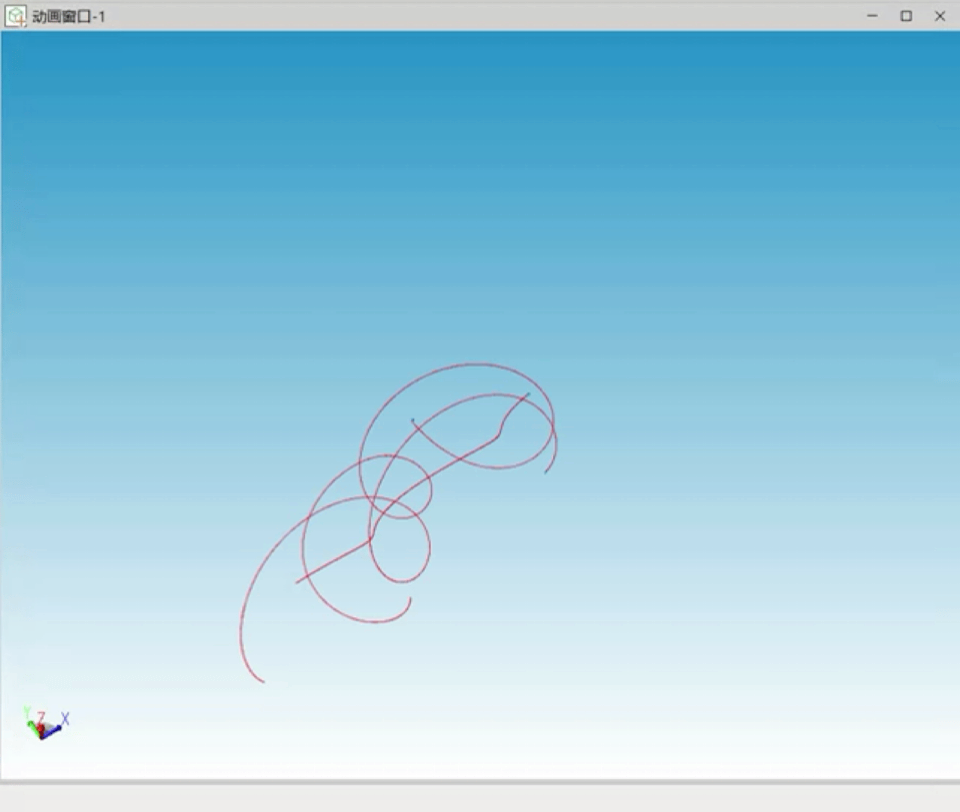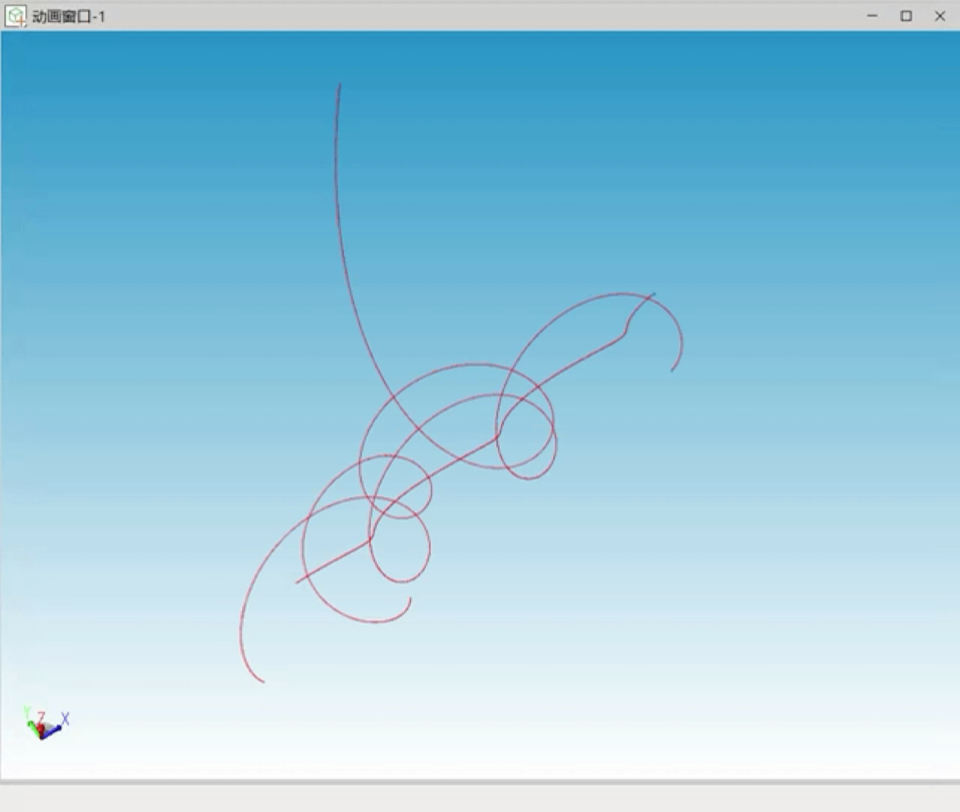
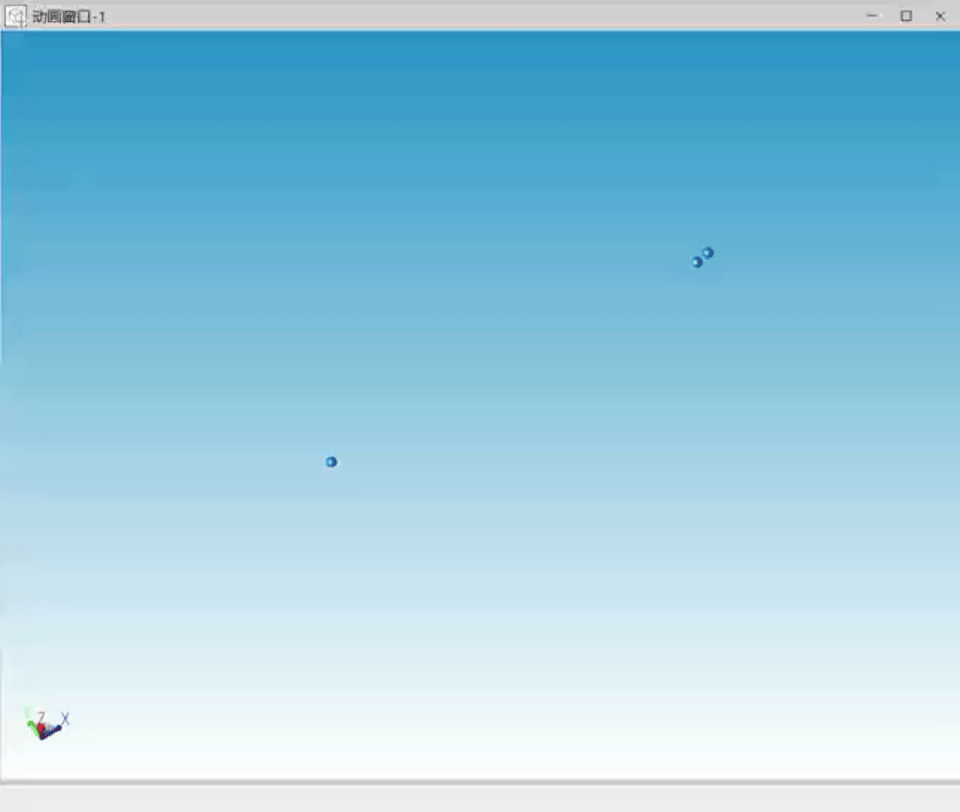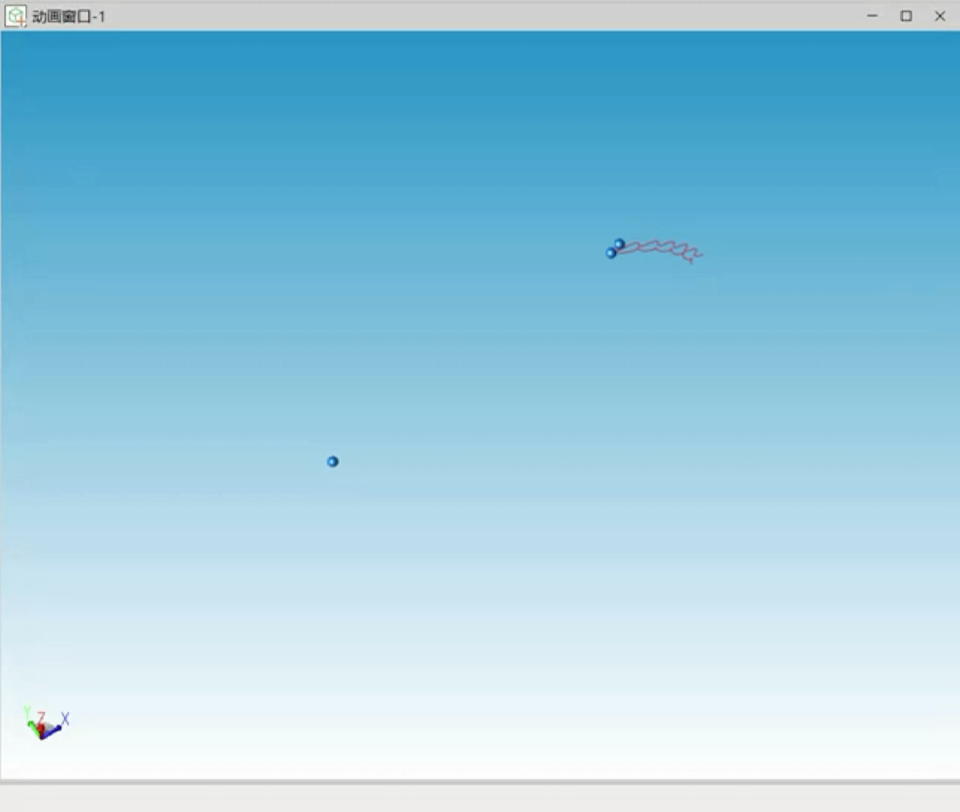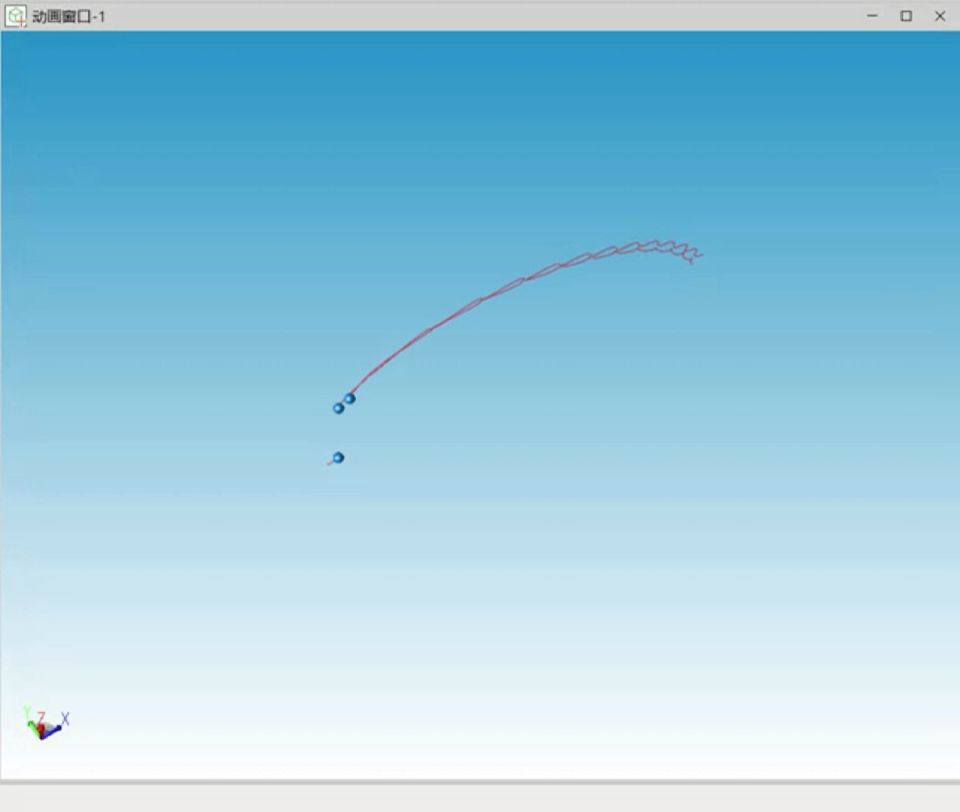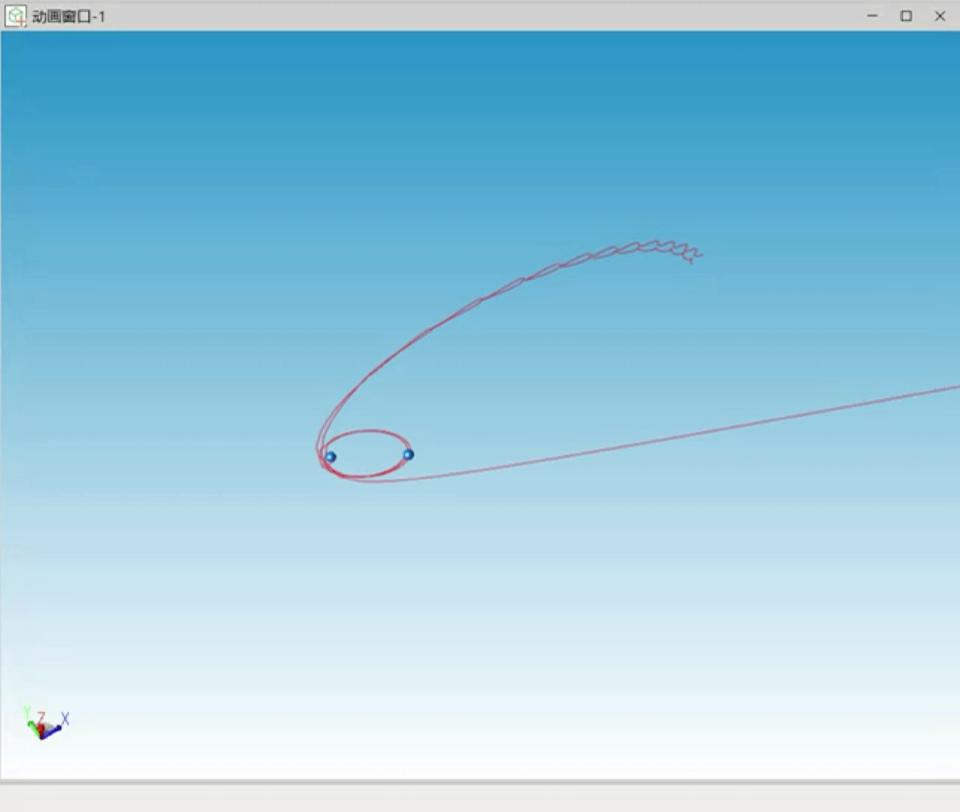
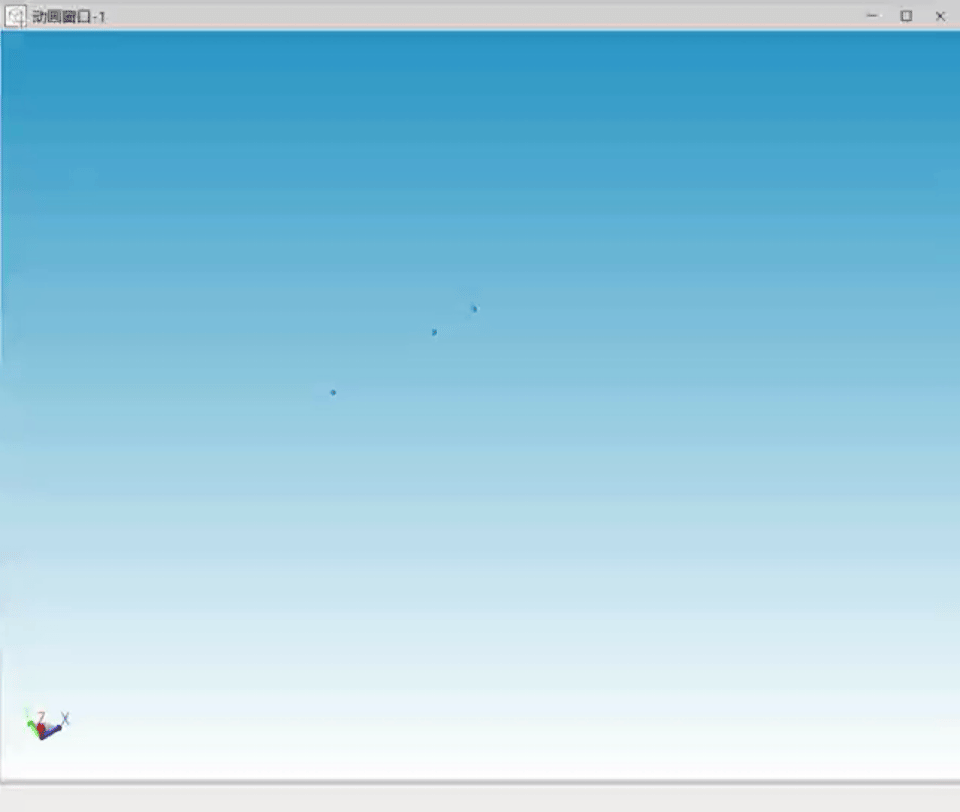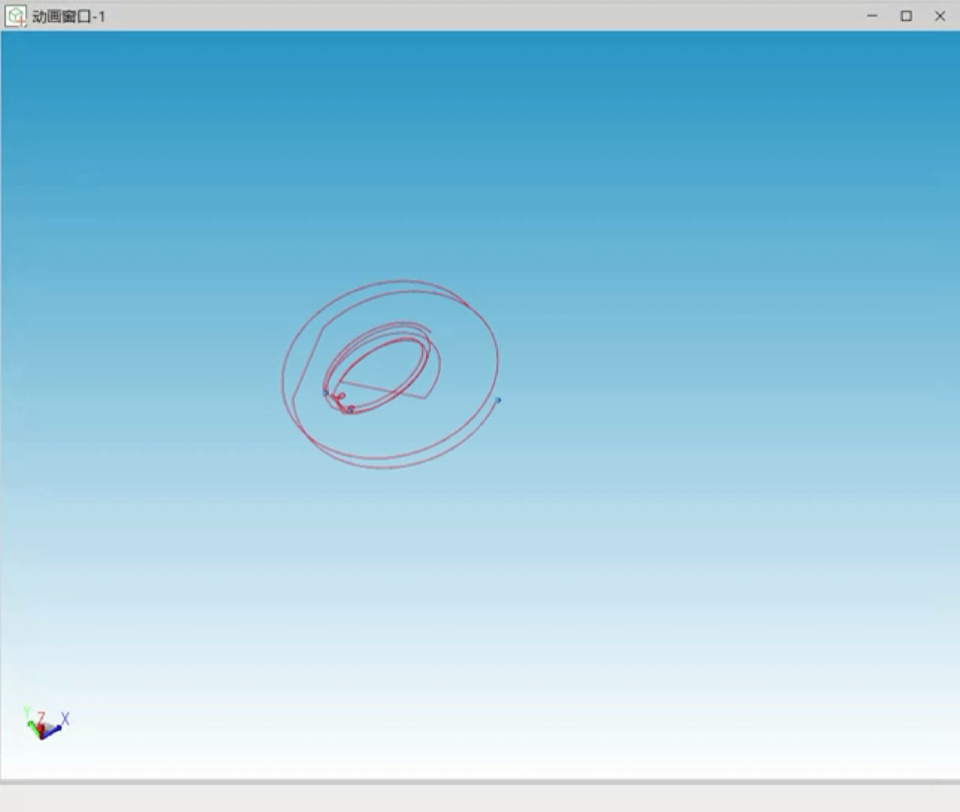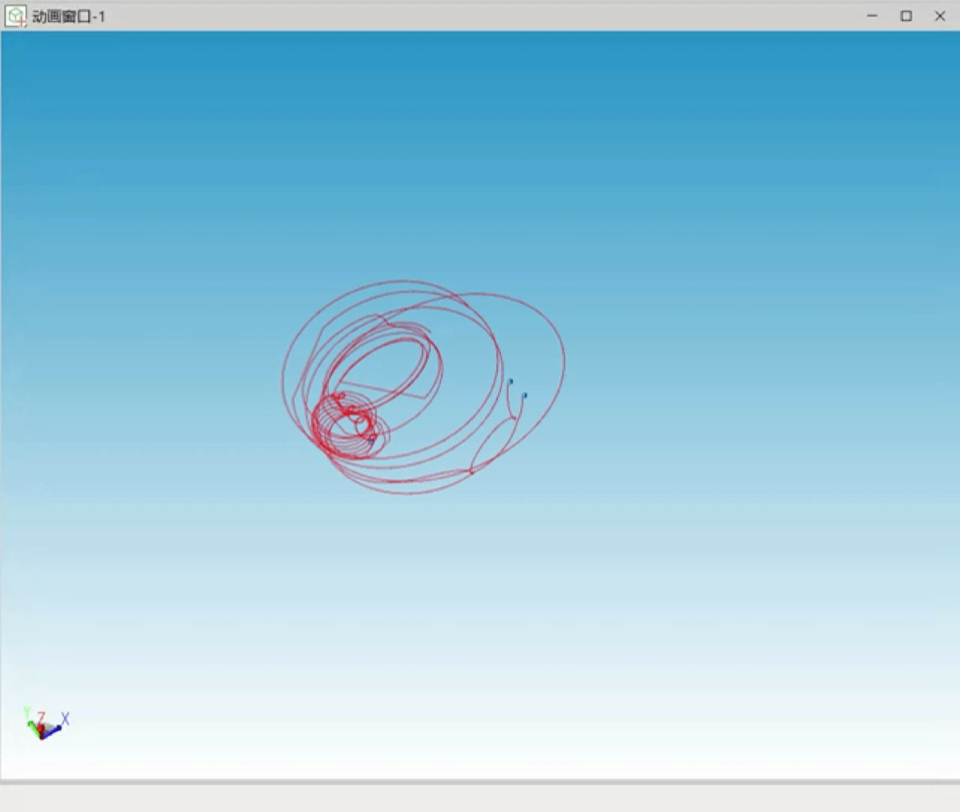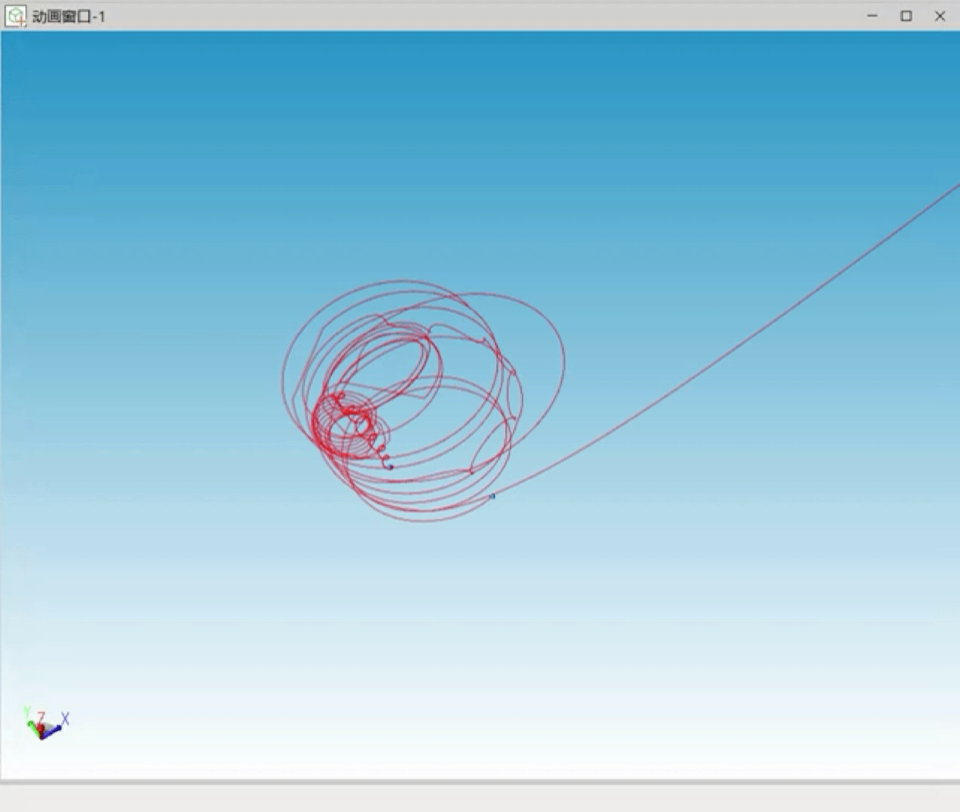
图7 不稳定解

在MWORKS中三体系统模型设置初始值的方式可直接通过设置状态变量的初值，选择三个天体的位置、速度为状态变量。例如图8为设置天体1的状态变量。

图8 设置天体1状态变量

设置天体1的初始位置和速度如图9所示。

图9 设置天体1初始位置和速度

【小贴士】在输入初值参数时，右侧提供“设置fixed属性”的小图钉，在未设定状态变量而又期望初始值设置生效时，非常有帮助。 

4  小结

基于本篇文章我们了解到了三体问题的由来、发展和混沌现象，并基于MWORKS.Sysplorer针对三体问题的特定情况建立了系统模型进行仿真，验证了不同初始状态对三体运动状态的重大影响。理论上，通过“基于MWORKS.Sysplorer从现有特解出发进行仿真模拟，不断调试初始条件直到新类型的轨道能具体化”方法，我们也可以发现三体的特解，为三体问题的科学进步作出贡献。

感兴趣的小伙伴可以利用MWORKS.Sysplorer进行仿真计算，一起开展三体运动研究，解救三体人于水深火热之中~