函数的微分与全微分

一、微分

1.1 定义

正方形金属薄片，函数$A=x^2$相应的增量$\Delta A$，即
$$\Delta A=(x_0+\Delta x{)}^2-x_0^2=2x_0\Delta x+(\Delta x{)}^2$$
当$\Delta x\to 0$时，第二部分$(\Delta x{)}^2$是比$\Delta x$高阶的无穷小，即$(\Delta x{)}^2=o(\Delta x)$。由此可见，如果边长改变很微小，即$|\Delta x|$很小时，面积的改变量$\Delta A$可近似第用第一部分来代替。

一般地，如果函数$y=f(x)$满足一定条件，那么增量$\Delta y$可表示为
$$\Delta y=A\Delta x+o(\Delta x)$$
其中A是不依赖于$\Delta x$的常数，因此$A\Delta x$是$\Delta x$的线性函数，且$\Delta y$与它的差
$$\Delta y-A\Delta x=o(\Delta x)$$
是比$\Delta x$高阶的无穷小。所以，当$A\ne 0$，且$|\Delta x|$很小时，可以用$\Delta x$的线性函数$A\Delta x$来近似替代$\Delta y$。

定义：设函数$y=f(x)$在某区间内有定义，$x_0$及$x_0+\Delta x$在这区间内，如果函数的增量
$$\Delta y=f(x_0+\Delta x)-f(x_0)$$
可表示为
$$\Delta y=A\Delta x+o(\Delta x)$$
其中A是不依赖于$\Delta x$的常数，那么称函数$y=f(x)$在点$x_0$是可微的，而$A\Delta x$叫做函数$y=f(x)$在点$x_0$相应于自变量增量$\Delta x$的微分，记作$dy$，即
$$dy=A\Delta x$$
例1：求函数$y=x^2$在$x=1$处的微分

解：函数$y=x^2$在$x=1$处的微分为
$$dy=(x^2{)}^{\prime }{|}_{x=1}\Delta x=2\Delta x$$

函数$y=f(x)$在任意点x的微分，称为函数的微分，记作$dy$或$df(x)$，即
$$dy=f^{\prime }(x)\Delta x$$
例2：函数$y=cosx$的微分为
$$dy=(cosx{)}^{\prime }\Delta x=-sinx\Delta x$$
例3：求函数$y=x^3$当$x=2$,$\Delta x=0.02$时的微分

解：先求函数在任意点x的微分
$$dy=(x^3)’\Delta x=3x^2\Delta x$$
再求函数当$x=2,\Delta x=0.02$时的微分
$$dy{|}_{x=2,\Delta x=0.02}=(3x^2\Delta x){|}_{x=2,\Delta x=0.02}=3\cdot 2^2\cdot 0.02=0.24$$
通常把自变量x的增量$\Delta x$称为自变量的微分，记作$dx$，即$dx=\Delta x$，于是函数$y=f(x)$的微分又可记作
$$dy=f^{\prime }(x)dx$$
从而有
$$\frac{dy}{dx}=f^{\prime }(x)$$
这就是说，函数的微分$dy$与自变量的微分$dx$之商等于该函数的导数。因此，导数也叫做“微商”。

1.2 几何意义

在直角坐标系中，函数$y=f(x)$的图形是一条曲线。对于某一固定的$x_0$值，曲线上有一个确定点$M(x_0,y_0)$，当自变量x有微小增量$\Delta x$时，就得到曲线上另一点$N(x_0+\Delta x,y_0+\Delta y)$。

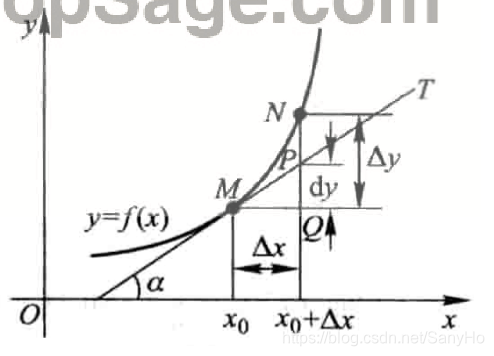
由图可知
$$\begin{gathered} MQ=\Delta x, \\ QN=\Delta y \end{gathered}$$
过点M作曲线的切线MT，它的倾角为$\alpha$，则
$$QP=MQ\cdot tan\alpha =\Delta x\cdot f^{\prime }(x_0)$$
即
$$dy=QP$$
由此可见，对于可微函数$y=f(x)$而言，当$\Delta y$是曲线$y=f(x)$上的点的纵坐标增量时，$dy$就是曲线的切线上点的纵坐标的相应增量。当$|\Delta x|$很小时，$|\Delta y-dy|$比|$\Delta x$|小得多。因此在点M邻近，我们可以用切线线段来近似代替曲线段。在局部范围内用线性函数近似非线性函数，在几何上就是局部用切线段近似替代曲线段，这在数学上称为非线性函数的局部线性化。

二、全微分

由偏导数定义知，二元函数对某个自变量的偏导数表示当另一个自变量固定时，因变量相对于该自变量的变化率。根据一元函数微分学中增量与微分的关系，可得
$$\begin{gathered} f(x+\Delta x,y)-f(x,y)\approx f_x(x,y)\Delta x, \\ f(x,y+\Delta y)-f(x,y)\approx f_y(x,y)\Delta y \end{gathered}$$
上面两式的左端分别叫做二元函数对x和对y的偏增量，而右端分别叫做二元函数对x和y的偏微分。

在实际问题中，有时需要研究多元函数中各个自变量都取得增量时因变量所获得的增量，即所谓的全增量问题。下面以二元函数为例进行讨论。

设函数$z=f(x,y)$在点$P(x,y)$的某邻域内有定义，$P^{\prime }(x+\Delta x,y+\Delta y)$为这邻域内的任意一点，则称这两点的函数值之差$f(x+\Delta x,y+\Delta y)-f(x,y)$为函数在点P对应于自变量增量$\Delta x$和$\Delta y$的全增量，记作$\Delta z$，即
$$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$$
一般说来，计算全增量$\Delta z$比较复杂。与一元函数的情形一样，我们希望用自变量的增量$\Delta x、\Delta y$的线性函数来近似地代替函数的全增量$\Delta z$，从而引入如下定义。

定义：设函数$z=f(x,y)$在点$(x,y)$的某邻域内有定义，如果函数在点$(x,y)$的全增量
$$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$$
可表示为
$$\Delta z=A\Delta x+B\Delta y+o(\rho )$$
其中A和B不依赖于$\Delta x$和$\Delta y$而仅与x和y有关，$\rho =\sqrt{(\Delta x{)}^2+(\Delta y{)}^2}$,那么称函数$z=f(x,y)$在点$(x,y)$可微分，而$A\Delta x+B\Delta y$称为函数$z=f(x,y)$在点$(x,y)$的全微分，记作$dz$，即
$$dz=A\Delta x+B\Delta y$$
如果函数在区域D内各点处都可微分，那么称这函数在D内可微分。

定理1（必要条件）：如果函数$z=f(x,y)$在点$(x,y)$可微分，那么该函数在点$(x,y)$的偏导数$\frac{\partial z}{\partial x}$与$\frac{\partial z}{\partial y}$必定存在，且函数$z=f(x,y)$在点$(x,y)$的全微分为
$$dz=\frac{\partial z}{\partial x}\Delta x+\frac{\partial z}{\partial y}\Delta y$$
定理2（充分条件）：如果函数$z=f(x,y)$的偏导数$\frac{\partial z}{\partial x}$、$\frac{\partial z}{\partial y}$在点$(x,y)$连续，那么函数在该点可微分。

以上关于二元函数全微分的定义及可微分的必要条件和充分条件，可以完全类似地推广到三元和三元以上的多元函数。

习惯上，我们将自变量的增量$\Delta x$与$\Delta y$分别记作$dx$与$dy$，并分别称为自变量x与y的微分。这样，函数$z=f(x,y)$的全微分就可写为
$$dz=\frac{\partial z}{\partial x}dx+\frac{\partial z}{\partial y}dy$$
通常把二元函数的全微分等于它的两个偏微分之和这件事称为二元函数的微分符合叠加原理。

叠加原理也适用于二元以上的函数。例如，如果三元函数$u=f(x,y,z)$可微分，那么它的全微分就等于它的三个偏微分之和，即
$$du=\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy+\frac{\partial u}{\partial z}dz$$