1. 问题引入——“以直代曲”——以直线近似曲线,“以平代曲”——以平面近似曲面
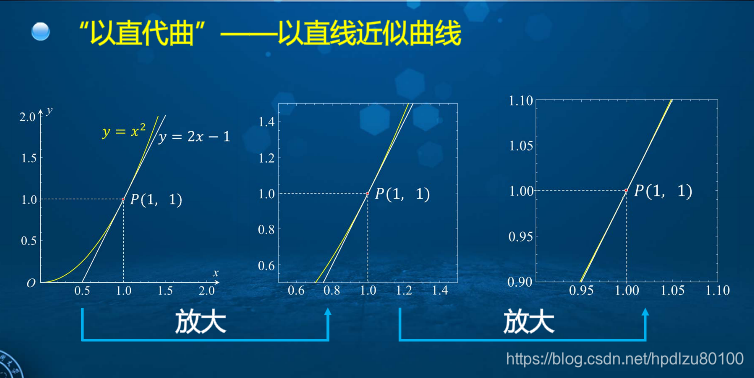

2. 一元函数微分的概念(线性逼近,可微与可导等价,以直代曲)

3. 二元函数的微分(偏增量,偏微分,全增量)

4. 二元函数的切向量、切平面(假设二元函数具有一阶连续偏导数)

5. 二元函数的局部线性近似(局部线性化函数)




6. 局部线性近似函数

7. 二元函数的可微与全微分的定义



1. 问题引入——“以直代曲”——以直线近似曲线,“以平代曲”——以平面近似曲面


2. 一元函数微分的概念(线性逼近,可微与可导等价,以直代曲)

3. 二元函数的微分(偏增量,偏微分,全增量)

4. 二元函数的切向量、切平面(假设二元函数具有一阶连续偏导数)

5. 二元函数的局部线性近似(局部线性化函数)




6. 局部线性近似函数

7. 二元函数的可微与全微分的定义



 3891
3891
 878
878

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


