支持向量机SVM在python下的使用

这里我们将简要介绍下SVM是什么，然后将做一些SVM的经典例子，其中也会结合一些其他的算法来完成这些例子
我的配置：Python 3.7+, Pycharm

一 SVM介绍

1.1 SVM可以做什么

1. 手写数字识别
   目前最好的识别水平：
   • LeNet 4（错误率<0.7%）
   • 多项式支持向量机（错误率<0.8%）
2. 性别识别
   通过SVM来判断是男还是女
3. 行人检测

1.2 SVM的理论基础

1.2.1 超平面的描述

在数学中，超平面是n维欧氏空间中余维度等于1的子空间，即n维空间中的超平面使n-1维的子空间。这是平面中的只献，空间中的平面的推广
设$F$为域（可以先将F视为实数集R），n维空间$F^n$中的超平面是由以下方程确定的：
$$a_1{x}_1+....+a_n{x}_n=b$$
这个看起来是一个由多变量组成的平面，接下来我们用数学概念来理解它

① 低维空间上对超平面的简单了解

理解：高中数学课本上的“点动成线，线动成面，面动成体”

我们先从低维空间出发，在低维空间中简单的来理解超平面：

1. 一维空间中，只有一个维度，一维坐标系为：$$a_1{x}_1+b=0$$在一维空间上确定了一个点，点则是一维空间上的超平面
2. 二维空间上，由两个维度，为平面直角坐标系：$$a_1{x}_1+a_2{x}_2+b=0$$在二维空间上确定了一条直线，则直线是二维空间上的超平面
3. 三维空间中，三个维度，三维坐标系:$$a_1{x}_1+a_2{x}_2+a_3{x}_3+b=0$$在三维空间上确定了一个平面，则平面是三维空间上的超平面
4. 以此类推到n维空间上，感觉有点像降维打击和层层升级的感觉hmmm

② 系统论证（可略）

n维空间中的超平面可以由以下方程给出：
$$a_1{x}_1+a_2{x}_2+....+a_n{x}_n+b=0$$
令$w$和$x$都是n维列向量，$x$是$n$维空间上的法向量，$b$是一个师叔，代表圆点到超平面的距离，则有：
$$\begin{gathered} x=(x_1,x_2,...,x_n{)}^T \\ a={a_1,a_2,...,a_n}^T \\ 改写成 \\ {a}^{T}x+b=0 \end{gathered}$$
在这里，我们从三维空间出发，在三维空间中，平面的定义为：
$$a_1{x}_1+a_2{x}_2+a_3{x}_3+b=0$$

注：不同地方的平面方程形式会有不同，但都可以化成以上形式，只是系数会有所不同，这里为了统一，采用上述形式

这个平面方程是线性的，即由三维空间上点的三个分量的线性组合构成，容易知道，这里的方程数量为1，类推到高维空间上，则有了超平面的概念（去掉变量，保留变量这类的操作）。因为超平面是平面中的直线，空间中平面的推广，所以当维度大于3时，才可以被称为超平面
超平面的本质时自由度比空间维度小1，那么如何理解自由度呢？

③ 自由度

数学上，自由度是一个随机向量的维度数，也就是一个向量能被完整描述所需要的最少单位向量数¹

简单理解：自由度是在当前维度空间的点至少要给定几个分量才能确定它，在一开始的用低维空间中的例子中正好说明了这点
超平面H是从$n$维空间到$n-1$维空间的一个映射子空间，它有一个$n$维向量和一个实数定义
依然从三维空间出发：三维空间中点集$I=(x,y,z)$满足等式(I为一个平面):
$$\begin{gathered} Ax+By+Cz+D=0(A,B,C均为标量，且至少有一个不为0) \\ 假设C不为0，则： \\ z=-\frac{A}{C}x-\frac{B}{C}y-\frac{D}{C}, \\ 则I(x,y,z)=(x,y,-\frac{A}{C}x-\frac{B}{C}y-\frac{D}{C})=x(1,0,-\frac{A}{C})+y(0,1,-\frac{B}{C})+(0,0,-\frac{D}{C}) \end{gathered}$$
说明这个平面过$(0,0,-\frac{D}{C})$,法向量为$(A,B,C)$,这里是将z替换了，换成x，y会有不同的结果，但是法向量还会使$(A,B,C)$
在该平面上任取一点$(x_0,y_0,z_0)$,显然这个点与$(0,0,-\frac{D}{C})$的差向量与法向量$(A,B,C)$垂直
由平面方程的点法式可以写成
$$A(x-0)+B(y-0)+C(x-(-\frac{D}{C}))=0$$
将这个式子进行变换，令非零向量$n=(A,B,C)$,该空间中有一个点$p=(0,0,-\frac{D}{C})$
可以推得
$$(A,B,C)((x,y,z)-(0,0,-\frac{D}{C}))=0$$
则在三维空间上，超平面的点为$i$，则超平面的方程为
$$n\ast (i-p)=0$$

④ 进一步推广到n维空间上

给定$n$维空间上的一个点 p = { x 1 , x 2 , . . . , x n } p = \lbrace x_{1}, x_{2}, ..., x_{n}\rbrace p={x1​,x2​,...,xn​}和非零向量 a = { a 1 , a 2 , . . . , a n } a = \lbrace{a_{1}, a_{2}, ..., a_{n}}\rbrace \quad a={a1​,a2​,...,an​}满足$a(i-p)=0$
点集$i$与点$p$的差向量与$a$正交，则称点集$i$为通过点$p$的超平面，向量$a$为通过超平面的法向量
按照该定义，只有当维度大于3才能成为超平面，当然也可以把直线看成是二维空间的超平面，平面是三维空间的超平面。n空间内的一个n-1维的仿射子空间

如何判断超平面的正负？
在二维平面上，判断一个点和一条直线的位置，我们可以把这个点代入到直线方程中将它和0进行比较，如果等于0则在直线上，大于或小于0，则在直线的左右侧，推广到n维空间也是一样的，根据这个来判断就可以啦~

1.2.2 支持向量机的描述

目标： 找到一个超平面，使得它能够尽可能多的将两类数据点正确的分开，同时使分开的两类数据点距离最远
解决方法： 构造一个在约束条件下的优化问题，具体的说是一个约束二次规划问题，通过求解该问题，得到分类器
定义：

• 支持向量： 为支持或支撑平面的构造中起作用的向量,对于线性可分，支持向量使两类样本中离分类面最近的点
• 机（机器）： 这里指的其实是一个算法，在ML中，我们经常把一些算法看做是一个机器，如分类机（分类器），而SVM本身就是一种监督学习的方法，它可以广泛的应用到统计分类以及回归分析中

1.3 线性SVM：可分情况

线性可分意味着存在超平面使训练点中的正类和负类样本分别位于该超平面的两侧

跟我们上面所构造的超平面方程一样，假设现在有一个方程：
$$(w\cdot x)+b=0$$
如果能确定这样的参数对$(w,b)$的话，就可以构造决策函数来进行识别新样本，决策函数的结果只有1和-1
$$f(x)=sgn((w\cdot x)+b)$$
线性可分情况下的最优分类线：

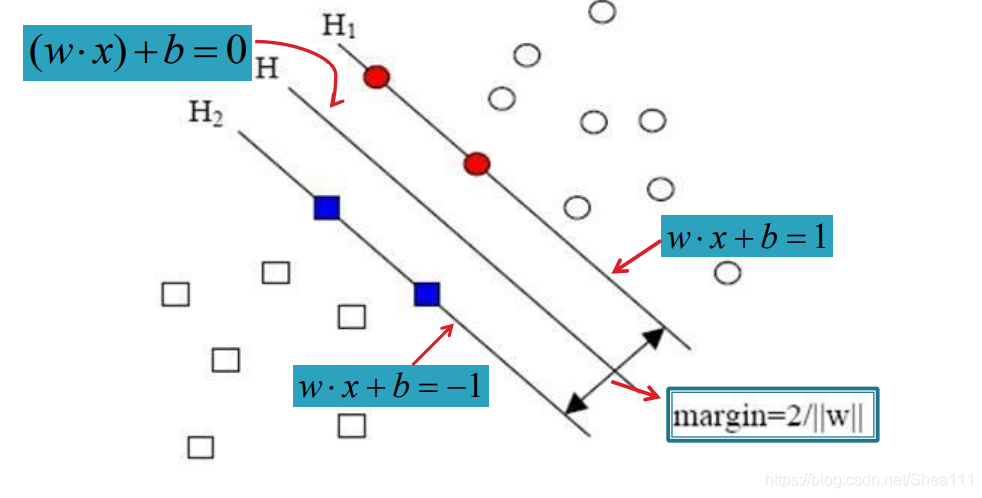
在选择分类线的过程中，我们的过程为：

1. 对于任意学习样本，其分布一定在直线之上或者直线之下，即有：
   $$\begin{gathered} w\cdot x_1+b\ge 1如果y_i=1 \\ w\cdot x_1+b\le -1如果y_i=-1 \end{gathered}$$
2. 将以上两式合并，则有：
   $$y(w\cdot x_1+b)\ge 1,i=1,2,...,N$$
3. 在选择分类线的过程中，上式对于任何学习样本都必须成立，在此前提下寻找最宽边界的问题，最后可以表示成一个约束优化问题：
   $$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||w|{|}^2 \\ s.t.y_i((w\cdot x_i)+b)\ge 1,i=1,...,n \end{gathered}$$
   如何求解这个方程，不再作多的讲解，感兴趣的朋友可以必应或Google以下都应该有的

1.4 线性SVM：不可分情况

现在考虑线性不可分情况，对于训练集$D$,不存在这样的超平面，使训练集关于该超平面的几何间隔取正值。如果要用超平面来划分的话，一定会有错分的点

但我们仍希望使用超平面进行划分，这个时候应该软化对间隔的要求，即容许不满足约束条件的样本点存在
对于线性可分我们构造的方程是：
$$y_i((w\cdot x_i)+b)\ge 1$$
为此，我们引入松弛变量${\xi }_i\ge 0$，并“**软化”**约束条件：
$$y_i((w\cdot x_i)+b)\ge 1-{\xi }_i,i=1,...,n$$
为了避免$\xi$取太大的值，需要在目标函数中对它们进行惩罚，于是原始优化问题 变为 ( 其中C称为惩罚因子)：
$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^n{\xi }_i \\ s.t.y_i((w\cdot x_i)+b)\ge 1-{\xi }_i,i=1,...,n{\xi }_i\ge 0 \end{gathered}$$
这个时候支持向量有下列性质：

• 界内支持向量一定位于间隔边界上的正确划分区；
• 支持向量不会出现在间隔意外的正确划分区
• 非支持向量一定位于带间隔的正确划分区
  

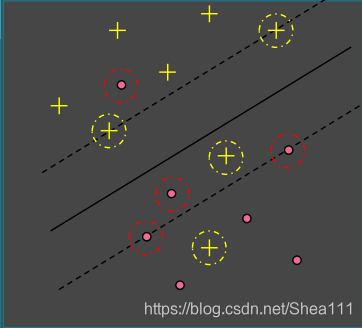
1.5 非线性SVM

对于一般的非线性情况—对于训练集T，无法找到之前的超平面来划分

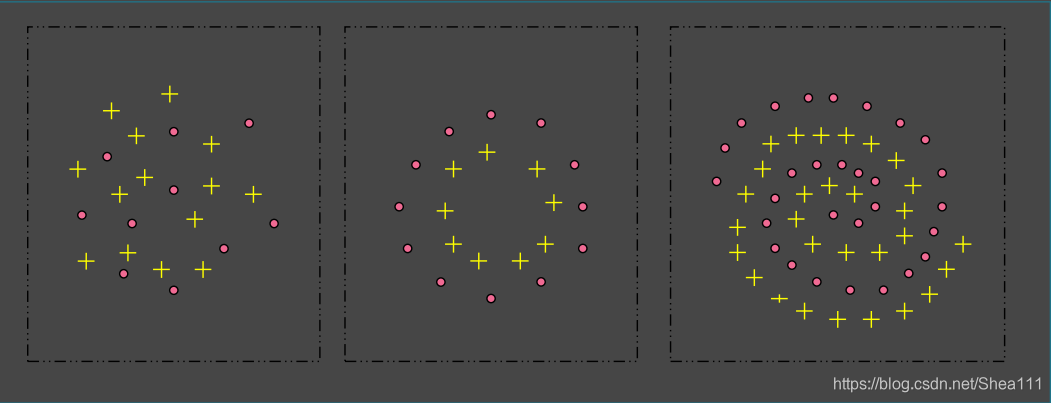
在这个时候我们通过核技术来处理，引入一个 非线性映射$\varphi$ 把输入空间 映射到一个（高维的）$Hilbert$空间$H$，使数据在H中是线性可分或线性不可分

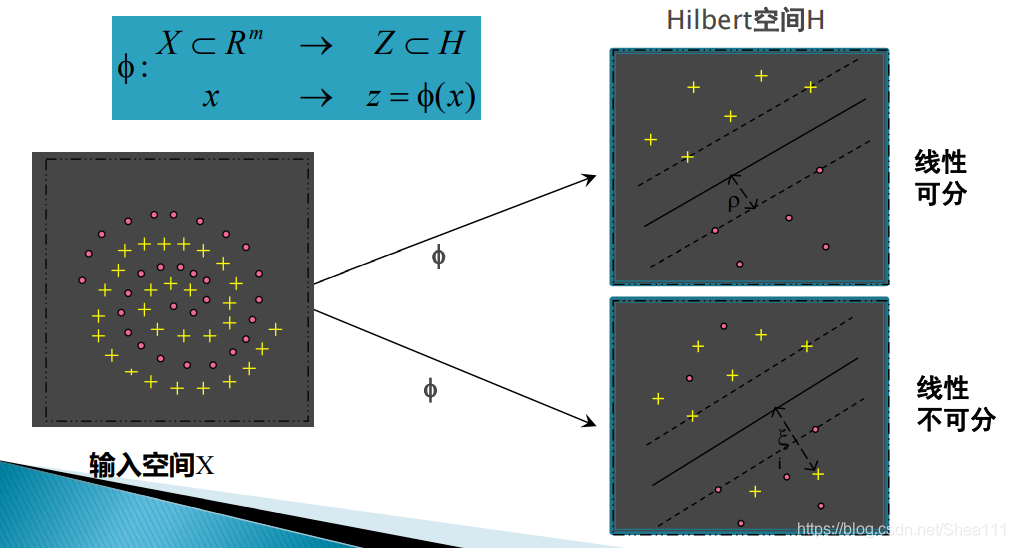
这个过程即为：

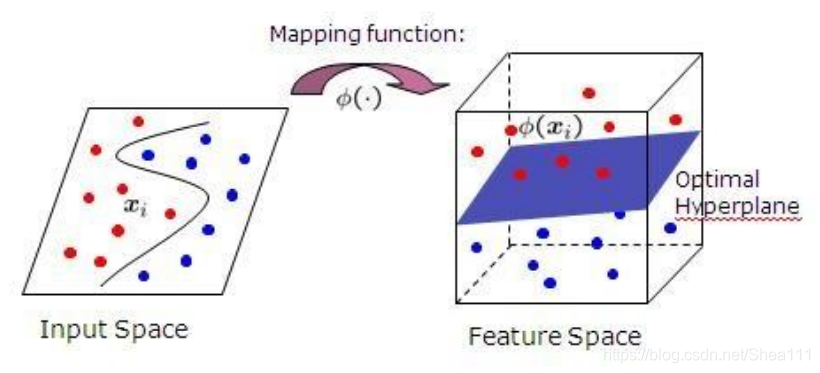
常用核函数：

• 线性核： $K(x\cdot x^{\prime })=(x\cdot x^{\prime })$
• 多项式核：$K(x\cdot x‘)=((x\cdot x’)+c{)}^d$
• 高斯RBF核：$K(x\cdot x^{\prime })=exp(-||x-x^{\prime }|{|}^2/{\sigma }^2)$
• Sigmoid核：$K(x\cdot x‘)=tanh(K(x\cdot x’)+v)$

核的比较：

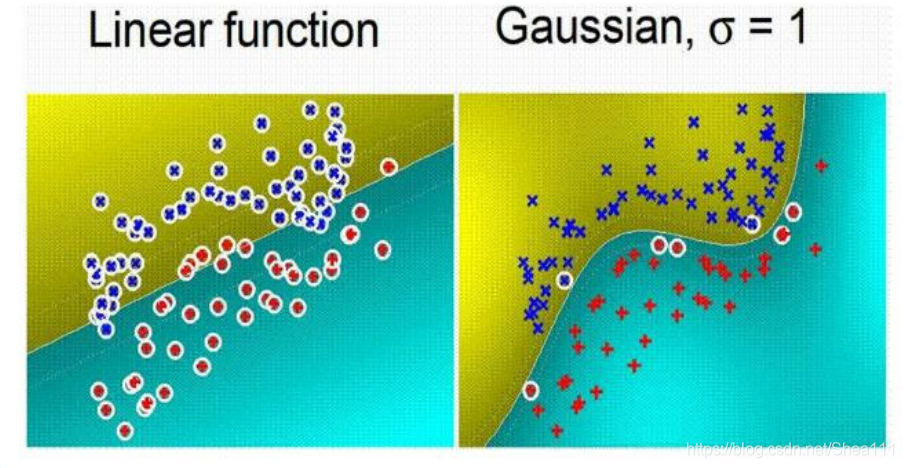
1.6 SVM的特点

SVM实现了高效的从训练样本到预报样本的“转导推理”，大大简化了通常的分类核回归问题
SVM的最终决策函数只由少数的支持向量决定，计算的复杂性取决于支持向量的数目，而不是样本空间的维数，这在某种意义上可以避免“维数灾”；如果说神经网络是对样本所有因子加权的话，SVM方法是对只占样本数的支持向量样本“加权”。而当预报因子与预报对象间蕴含的复杂非线性关系还不清楚的时候，基于关键样本的方法可能由于基于因子的“加权”
少数的支持向量决定了最终的结果，这不但能帮助我们抓住关键样本，“剔除”大量的冗余样本，而且这个方法不但算法简单，还具有比较好的“鲁棒性”。

二 SVM在MNIST上的使用

这里利用sklearn库进行svm训练MNIST数据集，准确率一般都可以达到90%以上

2.1 相关代码

关于数据集，可以使用tensorflow.examples.tutorials中自带的,也可以到官网自己下载，我这里是直接调用了，在这个过程中我的tutorials不知道为什么没有，我是到github上tensorflow库的开源下载下来的，如果你的也没有可以尝试一下这个方法。

from sklearn import svm
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('MNIST_data', one_hot=False)
train_num = 10000
test_num = 2000

x_train = mnist.train.images
y_train = mnist.train.labels
x_test = mnist.test.images
y_test = mnist.test.labels

# 构建预测器
predictor = svm.SVC(gamma=0.03, C=100.0, decision_function_shape='ovr', kernel='rbf')
# 喂入数据
predictor.fit(x_train[:train_num], y_train[:train_num])
# 训练得出的结果
result = predictor.predict(x_test[:test.num])
# 得出结果
accurancy = np.sum(np.equals(result, y_test[:test_num])/test_num
print("准确率为："+accurancy)

结果：

准确率为：0.9595

2.2 SVC函数解析

gamma
SVM的间隔，即是超平面距离不同类别的最小距离，是一个float的值，可以自己规定，也可以使用SVM的值，SVM自己的值有两个选择

• auto: 选择auto时，这个时候gamma = 1/feature_num,即特征的数目之一
• scale: 选择scale时，这个时候gamma = 1/（frature_num*X.std()），特征数目乘样本标准差分之1，一般来说，scale比auto结果更准确

C（惩罚参数）
C作为松弛变量的参数，一般称为惩罚参数， 用来调整容忍松弛度， 当C越大，则说明这个模型对分类错误更加容忍，这也是为了避免过拟合
decision_funtion_shape
两个选择：

• ovr： one vs rest 将一个类别与其他类别进行划分
• ovo： one vs one 两两划分

kernel
核函数的选择

• 当样本线性可分的时候，一般选择linear作为线性核函数
• 样本线性不可分的时候，可以有很多选择，一般选择rbf，rbf即径向基函数，又称高斯核函数

三 SVM在ADULT上的使用

3.1 数据集介绍

本数据来源于UCI的Adult数据集，在这里我们使用LIBSVM包对这个数据进行分类
因为原始数据集由14个特征，分别是age,workclass,fnlwgt(final weight),education,education-num,marital-status,occupation,relationship,race,sex,captital-gain,captital-loss,hours-per-week和native-country，其中有6个特征是连续值，8个特征是离散值，所以一开始先要做的处理是：把连续特征离散化 ，将有M个类别的离散特征转换为M个二进制特征
因为Adult数据集一共有48842条数据，每条数据需要从原始特征的14个转换成123个，并以2：1的比例分为训练集核测试机；其中a9a是训练集，用来训练分类器模型；a9a-t是测试集，用来预测模型的分类效果。他们一共有2个类别，标签分别用-1和1来表示，代表1个人一年的薪资是否超过50k
变换后的数据下载地址：
Libsvm–Adult数据集

3.2 相关代码

这里我使用的是python的libsvm库，其实也可以直接下载libsvm进行使用，但是我比较喜欢直接用pycharm来敲，所以我这里选用的配置依旧是pycharm+pytho3.7+

把a9a和a9a.t文件放在工程的目录夹后，就可以开始操作啦

# 首先调用libsvm来训练分类器模型
from libsvm.commonutil import svm_read_problem
from libsvm.svmutil import *

y, x = svm_read_problem('a9a')
m = svm_train(y, x, '-c 5')

# 开始预测分类器的准确性
test_y, test_x = svm_read_problem('a9a.t')
p_label, p_acc, p_val = svm_predict(test_y, test_x, m)

最后结果：

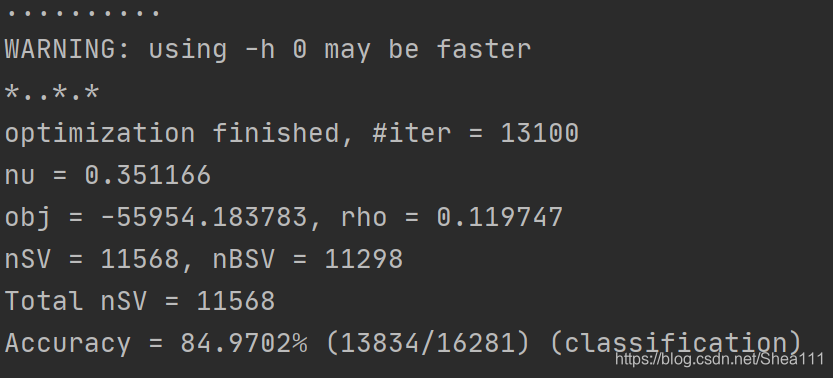
参数选项：

options:
-s svm_type : 设置SVM 类型，默认值为0，可选类型有
	0 -- C-SVC
	1 -- nu-SVC
	2 -- one-class SVM
	3 -- epsilon-SVR
	4 -- nu-SVR
	
-t 核函数类型：设置核函数类型，默认值为2，可选类型有
	0 -- 线性核: u'*v
	1 -- 多项式核: (gamma*u'*v + coef0)^degree
	2 -- RBF核（常用）: exp(-gamma*|u-v|^2)
	3 -- sigmoid核: tanh(gamma*u'*v + coef0)
	
-d degree : 
	set degree in kernel function (default 3)
	
-g gamma : 
	set gamma in kernel function (default 1/num_features)
	
-r coef0 : 
	set coef0 in kernel function (default 0)
	
-c cost : 
	设置C- SVC、e - SVR、n - SVR中从惩罚系数C，默认值为1
	
-n nu : 
	设置nu - SVC、one-class-SVM 与nu - SVR 中参数nu ，默认值0.5
	
-p epsilon : 
	核宽,设置e - SVR的损失函数中的e ，默认值为0.1；
	
-m cachesize : 
	设置cache内存大小，以MB为单位(默认40)：
	
-e epsilon : 
	设置终止准则中的可容忍偏差，默认值为0.001；
	
-h shrinking: 
	是否使用启发式，可选值为0 或1，默认值为1；
	
-b 概率估计: 
	是否计算SVC或SVR的概率估计，可选值0 或1，默认0；
	
-wi weight: 
	对各类样本的惩罚系数C加权，默认值为1；
-v n:
	n折交叉验证模式

其中-g选项中的k是指输入数据中的属性数

由此我们利用Libsvm和a9a的训练集得到的分类器模型在a9a测试集上的分类准确率约为84.97%

3.3 Libsvm使用总结

Libsvm的介绍、参数设置及应用

3.4 Adult数据集一般操作

目前大多是采用随机森林、朴素贝叶斯来进行预测，效果都是在85%附近，感兴趣的同学戳这两个链接：

1. 随机森林+SVM
2. 决策树+朴素贝叶斯

四 IRIS数据集

这里我们使用的是sklearn库里的svm， 数据准备直接从UCI下载iris.data即可

4.1 相关代码

import numpy as np
from matplotlib import colors
from sklearn import svm
from sklearn import model_selection
import matplotlib.pyplot as plt
import matplotlib as mpl


# *************将字符串转为整型，便于数据加载***********************
def iris_type(s):
    it = {b'Iris-setosa': 0, b'Iris-versicolor': 1, b'Iris-virginica': 2}
    return it[s]


#加载数据
data_path = 'iris.data'                                     # 数据文件的路径
data = np.loadtxt(data_path,                                # 数据文件路径
                  dtype=float,                              # 数据类型
                  delimiter=',',                            # 数据分隔符
                  converters={4: iris_type})                 # 将第5列使用函数iris_type进行转换
# print(data)                                               # data为二维数组，data.shape=(150, 5)
# print(data.shape)
# 数据分割
x, y = np.split(data,                                       # 要切分的数组
                (4,),                                       # 沿轴切分的位置，第5列开始往后为y
                axis=1)                                     # 代表纵向分割，按列分割
x = x[:, 0:2]                                               # 在X中我们取前两列作为特征，为了后面的可视化。x[:,0:4]代表第一维(行)全取，第二维(列)取0~2
# print(x)
x_train, x_test, y_train, y_test = model_selection.train_test_split(x,              # 所要划分的样本特征集
                                                                    y,              # 所要划分的样本结果
                                                                    random_state=1, # 随机数种子
                                                                    test_size=0.3)  # 测试样本占比


# **********************SVM分类器构建*************************
def classifier():
    # clf = svm.SVC(C=0.8,kernel='rbf', gamma=50,decision_function_shape='ovr')
    clf = svm.SVC(C=0.5,                         # 误差项惩罚系数,默认值是1
                  kernel='linear',               # 线性核 kenrel="rbf":高斯核
                  decision_function_shape='ovr') # 决策函数
    return clf


# 2.定义模型：SVM模型定义
clf = classifier()


# ***********************训练模型*****************************
def train(clf, x_train, y_train):
    clf.fit(x_train,         # 训练集特征向量
            y_train.ravel()) # 训练集目标值


# 3.训练SVM模型
train(clf, x_train, y_train)


# **************并判断a b是否相等，计算acc的均值*************
def show_accuracy(a, b, tip):
    acc = a.ravel() == b.ravel()
    print('%s Accuracy:%.3f' %(tip, np.mean(acc)))


def print_accuracy(clf, x_train, y_train, x_test, y_test):
    # 分别打印训练集和测试集的准确率  score(x_train,y_train):表示输出x_train,y_train在模型上的准确率
    print('training prediction:%.3f' % (clf.score(x_train, y_train)))
    print('testing prediction:%.3f' % (clf.score(x_test, y_test)))
    # 原始结果与预测结果进行对比   predict()表示对x_train样本进行预测，返回样本类别
    show_accuracy(clf.predict(x_train), y_train, 'training data')
    show_accuracy(clf.predict(x_test), y_test, 'testing data')
    # 计算决策函数的值，表示x到各分割平面的距离
    print('decision_function:\n', clf.decision_function(x_train))


# 4.模型评估
print_accuracy(clf, x_train, y_train, x_test, y_test)


def draw(clf, x):
    iris_feature = 'sepal length', 'sepal width', 'petal lenght', 'petal width'
    # 开始画图
    x1_min, x1_max = x[:, 0].min(), x[:, 0].max()  # 第0列的范围
    x2_min, x2_max = x[:, 1].min(), x[:, 1].max()  # 第1列的范围
    x1, x2 = np.mgrid[x1_min:x1_max:200j, x2_min:x2_max:200j]  # 生成网格采样点
    grid_test = np.stack((x1.flat, x2.flat), axis=1)  # stack():沿着新的轴加入一系列数组
    print('沿着新的轴加入一系列数组:\n', grid_test)
    # 输出样本到决策面的距离
    z = clf.decision_function(grid_test)
    print('样本到决策面的距离:\n', z)

    grid_hat = clf.predict(grid_test)  # 预测分类值 得到【0,0.。。。2,2,2】
    print('预测分类值:\n', grid_hat)
    grid_hat = grid_hat.reshape(x1.shape)  # reshape grid_hat和x1形状一致
    # 若3*3矩阵e，则e.shape()为3*3,表示3行3列

    cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'b', 'r'])

    plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)  # pcolormesh(x,y,z,cmap)这里参数代入
    # x1，x2，grid_hat，cmap=cm_light绘制的是背景。
    plt.scatter(x[:, 0], x[:, 1], c=np.squeeze(y), edgecolor='k', s=50, cmap=cm_dark)  # 样本点
    plt.scatter(x_test[:, 0], x_test[:, 1], s=120, facecolor='none', zorder=10)  # 测试点
    plt.xlabel(iris_feature[0], fontsize=20)
    plt.ylabel(iris_feature[1], fontsize=20)
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.title('svm in iris data classification', fontsize=30)
    plt.grid()
    plt.show()


# 5.模型使用
draw(clf, x)

4.2 结果展示

4.2.1 Console台：

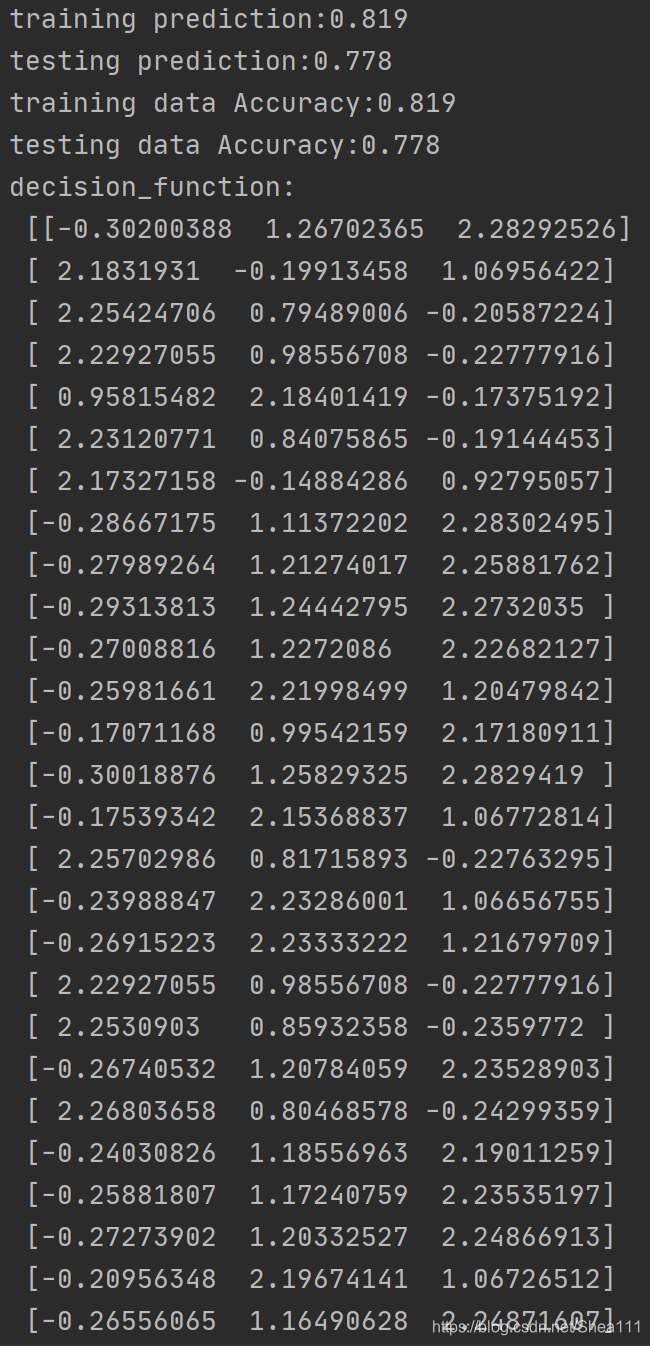
4.2.2 Figure图

① linear图

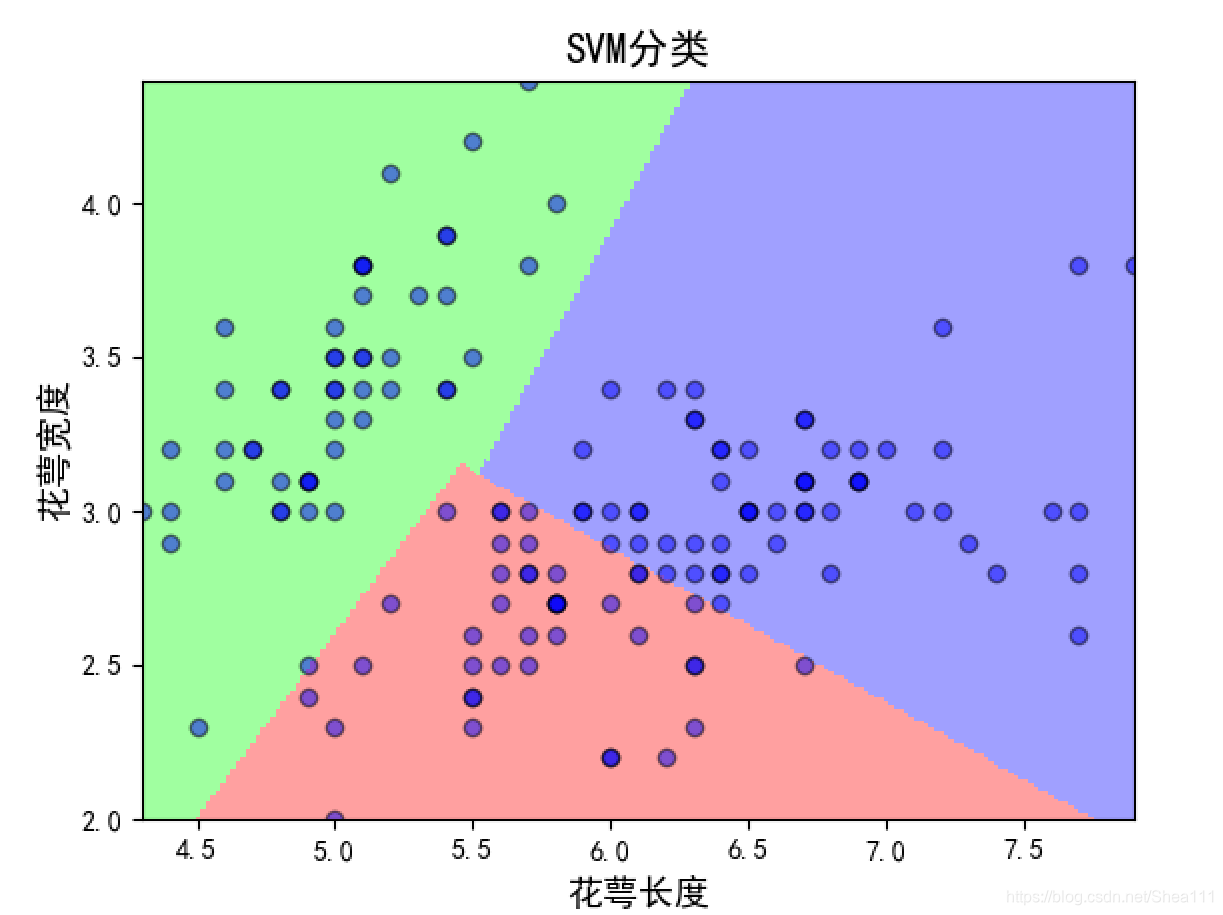
② rbf图

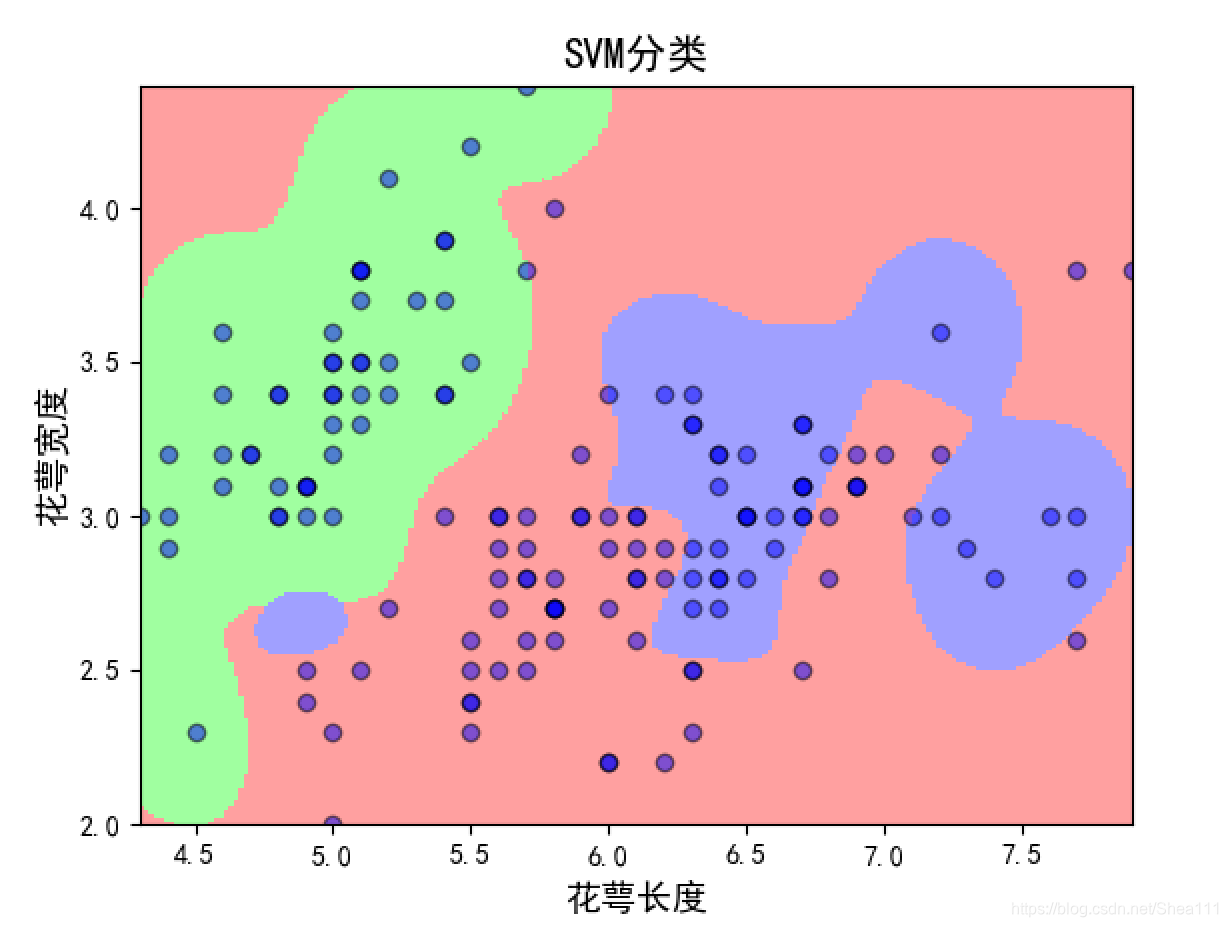
五 Abalone数据集–Regression

UCI上的数据集已经帮我们缩放到了[-1, 1]之间，但是当我用libsvm version='3.23.0.4"'中没有svm_scale这个，有可能是因为python中是不支持的，这个我训练出来的准确率也非常的低，即使改了很多个参数也是一样awa，希望有大佬给我指正一下代码哪里错了

from libsvm.commonutil import svm_read_problem
from libsvm.svmutil import *


y, x = svm_read_problem('abalone.txt')
m = svm_train(y, x, '-t 0 -c 4 -b 1')

test_y, test_x = svm_read_problem('abalone_scale.txt')
p_label, p_acc, p_val = svm_predict(test_y, test_x, m)

六 总结

libsvm库是十分好用的, 它的内置函数可以直接训练好模型，最后的这一块我把用libsvm是的基本操作讲一下，以下也是基于python的libsvm库， python处理成libsvm数据格式的方法为：https://blog.csdn.net/he99774/article/details/80389490

6.1 代码基本流程

# 导入必要库
from libsvm.commonutil import svm_read_problem
from libsvm.svmutil import * 

# 喂入数据
train_y, train_x = svm_read_problem(path) # 输入数据路径，
										  #一般都需要将数据改为libsvm的格式，必要时需要映射到[-1, 1]区间
#插一嘴，matlab应该是可以直接映射的，但python目前好像是不可以的

# 训练分类器
m = svm_train(y, x, '可选参数设置')

# 输入预测数据
test_y, test_x = svm_read_problem(path) # 测试数据
# 预测出结果
p_label, p_acc, p_val = svm_predict(test_y, test_x, m) 										  

6.2 分类器的参数设置

在3.2节，可以往上翻，根据需要的直接往里面填就好，示例：

m = svm_train(train_y, train_x, '-c 5 -b 1 -g 0.03') # 中间不用加分隔符

6.3 结果说明

一般console台会显示这些结果：

*.*
optimization finished,

#iter = 257
nu = 0.351161
obj = -225.628984, rho = 0.636110
nSV = 91, nBSV = 49
Total nSV = 91

在这里面

• #iter: 迭代次数
• nu: 与前面的操作参数-n nu相同
• obj: 为SVM文件转换为的二次规划求解得到的最小值
• rho: 为判决函数的常数项b
• nSV: 为支持向量个数
• nBSV: 为边界上的支持向量个数
• Total nSV: 为支持向量总个数

6.4 SVM优缺点

6.4.1 特点

• 非线性映射 是SVM方法的理论基础，SVM利用内积核函数代替向高维空间的非线性映射
• 对特征空间划分的最优超平面 是SVM的目标，最大化分类边际 的思想是SVM方法的核心
• 支持向量 是SVM的训练结果， 在SVM 分类决策 中决定作用的是支持向量
• SVM是一种有监视理论基础的新颖的小样本学习方法 ，它基本上不涉及概率测定及大数定律，因此不同于现有的统计方法，从本质上看，它避开了从归纳到演绎 的传统过程，实现了高效的从训练样本到预报样本 的“转导推理”
• SVM的最终决策函数 只由少数的支持向量所确定，计算的复杂数取决于支持向量的数目 ，而不是样本空间的维数 ，这在某种意义上避免了维数灾难
• 少数支持向量决定了最终结果，这不但可以帮助我们抓住关键样本，大量剔除冗余样本 ，而且这种方法不仅算法简单，还具有较好的鲁棒性
  鲁棒性体现在：
  1. 增、删非支持向量样本对模型没有影响
  2. 支持向量样本集具有一定的鲁棒性
  3. SVM方法对核的选取不敏感

6.4.2 不足

1. SVM算法对大规模训练样本难以实施 ，因为SVM是借助二次规划 来求解支持向量的，但是求解二次规划涉及到m阶矩阵的计算（m为样本的个数）， 当m很大时该矩阵的存储和计算将耗费大量的机器内存和运算时间。针对这些问题目前改进的算法有：
   • J.Platt ---- SMO算法
   • T.Joachims ---- SVM算法
   • C.J.C.Burges等 ---- PCGC
   • 张学工 ---- CSVM
   • O.L.Mangasar等 ---- SOR算法
2. 用SVM解决多分类问题存在困难 ，经典的SVM只给出了二类分类，如果要解决多类分类，需要使用多个二类支持机，即’ovr’，‘ovo’以及SVM决策树

6.5 帮助使用博客

这一篇博客是我觉得入门LIbsvm讲解最详细的一篇
libsvm使用心得

---

1. 参考资料：Wiki百科 ↩︎