读取编码器的计数脉冲转化成ROS的odom数据

1，理论模型

1.1 原理

如下图所示，蓝色圆形区域为小车的地盘，左右轮之间的间距为wheel_dist，注意算法中的所有的单位，全部是国际标准单位。移动机器人编码器，安装在左右轮上，机器人地底盘的坐标系为base_link坐标系，里程计坐标系为odom。

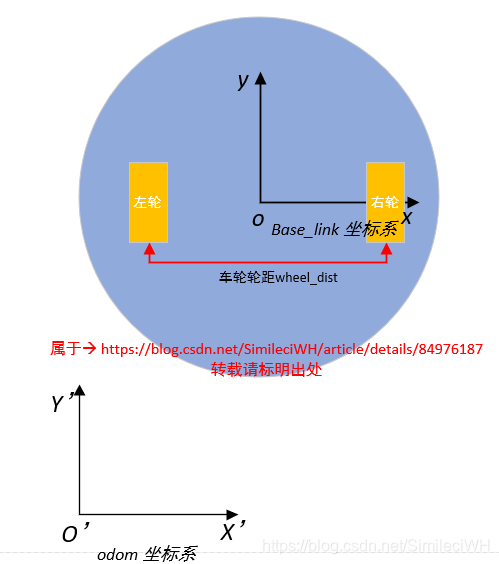
当移动机器人移动时，假设运动到如下图所示位置。图中的，V为移动小车中心点的运动速度方向，dxy_avg为移动小车中心点的运动距离。

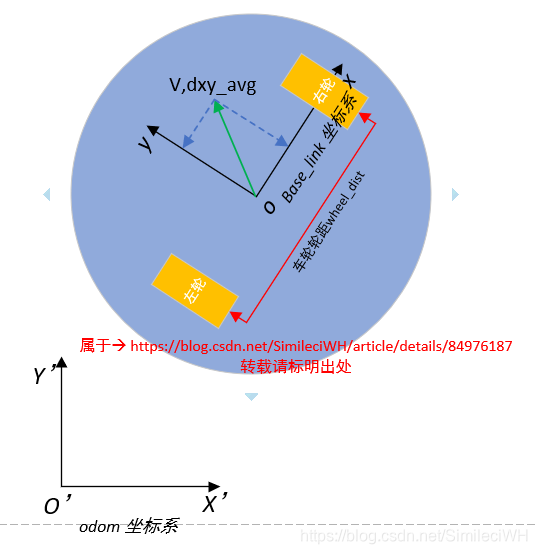
根据编码器的差值，可知前一时刻与当前时刻编码器增量的计数脉冲，已知小车车轮行走一个周长的长度的编码器计数脉冲个数，可以推算出，一个计数脉冲的移动距离。代码实现如下：

# (4096 * 7.5) dright is right boot position
dright = (right_enc - enc_right) * pi * D / (4096 * 7.5)
# dleft is left boot positon
dleft = (left_enc - enc_left) * pi * D / (4096 * 7.5)

其中，dright 为右轮的移动距离，dleft 为左轮的移动距离right_enc - enc_right为右轮编码器脉冲个数的增量，left_enc - enc_left为左轮编码器脉冲个数的增量，参数pi * D / (4096 * 7.5)，需要依据自己的小车测量出，编码器一个计数脉冲对应的行走距离（单位m）。

1.2 向中心点换算

因为在使用里程计向上层的开发中，往往对于小车模型，通常会考率成中心点的运动模型，即大致认为时一个质点，这是不准确的。算法如下：

 dxy_ave = (dright + dleft) / 2.0
 dth = (dright - dleft) / wheel_track
 vxy = dxy_ave / dt
 vth = dth / dt

其中， dxy_ave为左右轮的移动距离均值，认为是中心点的移动距离；dth 为通过为中心点的转动角度，通过弧长公式 $\theta =l/R$，中心点速度V=vxy 为位移对时间的微分$v=dx/dt$，vth 为角速度，为转动角度对时间的倒数 v t h = θ / d t vth= \theta/dt