SVD在推荐系统中的应用

1.SVD简介

SVD 技术是线性代数中的一种用于降低数据维度的矩阵分解技术，将高维的用户-项目评分矩阵分解成了低维的用户特征向量矩阵、项目特征向量矩阵以及包含奇异值的对角矩阵。

 2.关于SVD的分解原理

说明：具体的特征值、SVD分解的几何意义请参考博客。

奇异值分解(SVD)原理与在降维中的应用 - 刘建平Pinard - 博客园奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是https://www.cnblogs.com/pinard/p/6251584.html

SVD的分解公式如下：

 

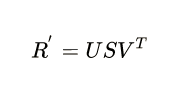
 其中为正交矩阵，为对角阵，为正交矩阵。

其分解示意图如下:

 

奇异值分解保证了原矩阵中的信息量，得到秩为k的最佳逼近矩阵，即包含原矩阵信息量超过特定阈值的近似矩阵。阈值 可以定义为前 k 个较大奇异值的平方和与全部奇异值平方和的比值，当给定时就可以求出k 值，从而得到最佳逼近矩阵。阈值的计算公式如下:

 

 其中为对角矩阵S的前 k 个较大奇异值的平方和,为对角矩阵S所有奇异值的平方和。

大多数情况下，只需要对角阵Σ前 10%的奇异值就能够拥有原矩阵 99%以上的信息量，根据如下公式可以算出k的大小

其中k是满足上式的最小整数，一般远小于m、n。

然后取出对角阵S的前 k 个奇异值构造新的对角阵,并从U 和V中取出对应的奇异值特征向量，组成两个新的正交矩阵,组成两个新的正交矩阵和,因此可以得到预测矩阵,是带有预测评分的矩阵近似于,公式如下:

 

其分解示意图如下:

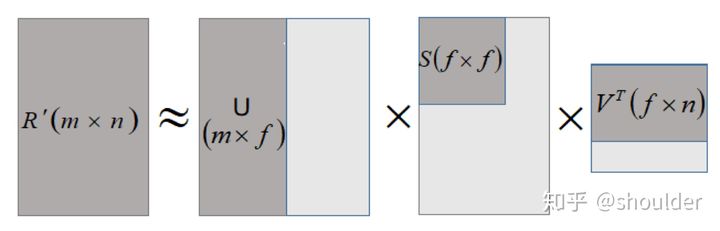
 上图中浅颜色表示原始数据，深颜色表示矩阵近似计算需要的数据。

 3.SVD在推荐系统中的应用举例

步骤一首先构造出一个用户对于电影的评分矩阵，如下图：

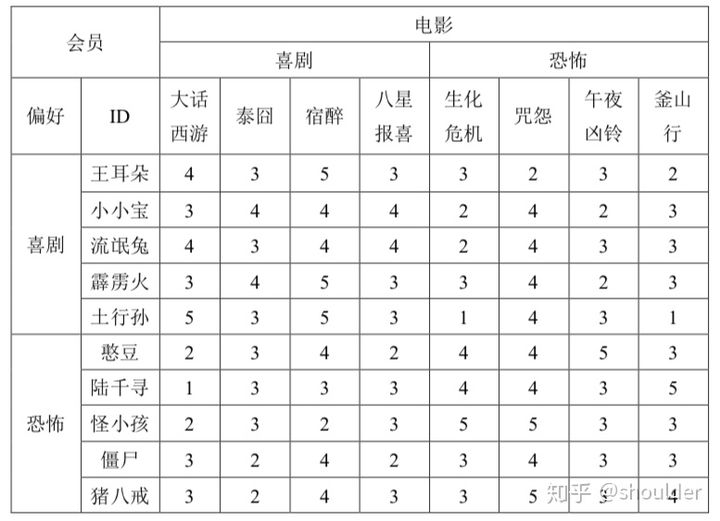
 步骤二对该矩阵进行分解，建议使用在线SVD计算器（下面是网址）

 在线奇异值分解(SVD)http://www.yunsuan.info/cgi-bin/singular_value_decomp.py

计算之后求得对应 的非零奇异值为{ = 29.3，= 5.9，= 3.1，= 2.5， ⋯ },，由于奇异值下降的速度非常快所以矩阵的信息量集中分布在前几个较大的特征值上，我们取前两个特征值。

前两个特征值对应右奇异矩阵的特征向量为：

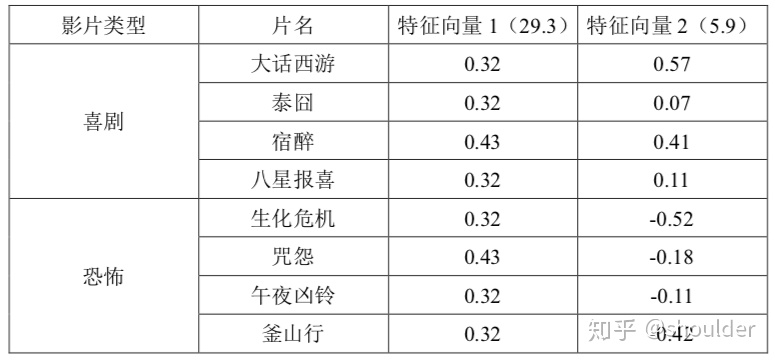
 前两个特征值对应左奇异矩阵的特征向量为：

 接下来我们利用公式和下图来计算用户u对于电影i的预测评分

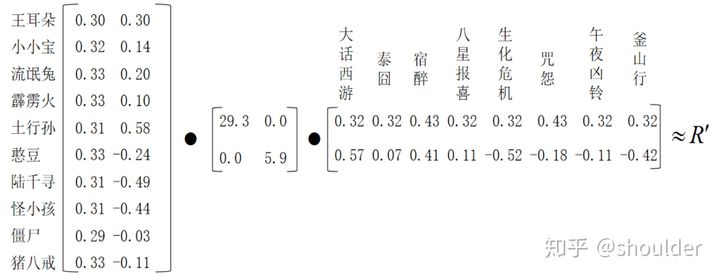
 我们可以计算出王耳朵对于午夜凶铃的评分为2.62，怪小孩对于釜山行的评分为4.00。

 

步骤三结果测评

王耳朵的观影历史显示其对喜剧类的电影评分较高，对恐怖电影普遍评分较低，因此可以推测她应该是不喜欢看午夜凶铃的，SVD模型给出的评分为2.62，与实际情况是相符的。

怪小孩的观影历史显示其对恐怖类的电影评分较高，对喜剧电影普遍评分较低，因此可以推测他应该是喜欢看釜山行的，SVD模型给出的评分为4.00，与实际情况是相符的。