基于Python的指数基金量化投资 - 正三角和倒三角投资模型

小将前行

于 2022-05-12 15:33:47 发布

阅读量3.7k

点赞数

分类专栏：指数基金量化投资文章标签： python

本文链接：https://blog.csdn.net/SocratesNietzsche/article/details/124732086

版权

本文探讨了两种指数基金投资策略——正三角和倒三角模式。正三角模式在低位买入更多，高位买入更少，降低投资成本，而倒三角则相反。通过比较，正三角模式在市场上涨时收益更高，下跌时亏损更小，是更为稳健的投资选择。文章提供源码并分享了实际应用中的数据和观察结果。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

普通投资者的投资方式中，有两种非常常见：

追涨杀跌式：涨了跟着买，跌了赶紧卖。

低买高卖式：跌了就买入，涨了就卖出。

第一种方式长期来看肯定是要亏钱的，长期追高难免不站岗，而第二种方式是比较正确的投资方式，但低买高卖要根据固定的指标来进行量化才能形成有效的模式。

如果把这两种投资方式进行量化，第一种称为倒三角投资模式，第二种称为正三角模式。
在这里插入图片描述
下面举两个例子来说明两种模式的差别（下面每一份代表买入1000元）。

倒三角模式就是指数高位的时候买得多，越高买得越多，而低位的时候买得少，越低买得越少，最后份额累积起来就形成了一个倒三角。最终的投资成本较高。
在这里插入图片描述
上图中是倒三角模式的一个例子，在指数低位的时候2700只买入了2份，随着指数向上，买入的份额越来越多，到指数变成3300时，买入了8份，这样算下来，买入的成本是3068.73。

正三角模式刚好和倒三角相反，指数高位的时候买得少，越高买得越少，而低位的时候买得多，越低买得越多。最终的投资成本较低。
在这里插入图片描述
上图中是正三角模式的一个例子，在指数低位的时候2700只买入了8份，随着指数向上，买入的份额越来越少，到指数变成3300时，只买入了2份，这样算下来，买入的成本是2908.79。

倒三角投资是不稳的，指数下跌的时候，份额集中在高位，下跌带来的亏损会被放大；而指数上涨的时候，由于成本较高，获得的收益也非常有限。

当指数上涨到3300点的时候，获得收益是(3300-3068.73)/3068.73=7.54%；而当指数下跌到2700点的时候，回撤亏损是(2700-3068.73)/3068.73=-12.02%

正三角投资就非常稳健，由于份额集中在低位，整个拉低了投资成本，指数下跌亏损有限，而指数如果上涨到和倒三角同样的指数点位会带来的更多的收益。

当指数上涨到3300点的时候，获得收益是(3300-2908.79)/2908.79=13.41%；而当指数下跌到2700点的时候，回撤亏损是(2700-2908.79)/2908.79=-7.18%
在这里插入图片描述
对比起来看，正三角和倒三角投资模式的区别是非常明显的，上涨到高位3300点，正三角会比倒三角将近多6个百分点的收益；而下跌到低位2700点，正三角会比倒三角将近少5个百分点的亏损。

下面来看看上证红利通过倒三角和正三角的投资比较，数据取上证红利指数成立以来的所有数据（2005年到目前的所有数据），而投资的区间取1300点到4000点之间，下图是上证红利的指数曲线，其中蓝线是1300点的位置，红线是4000点的位置。
在这里插入图片描述
投资过程中每隔300点增加或减少一份投入（一份投入=1000块钱）

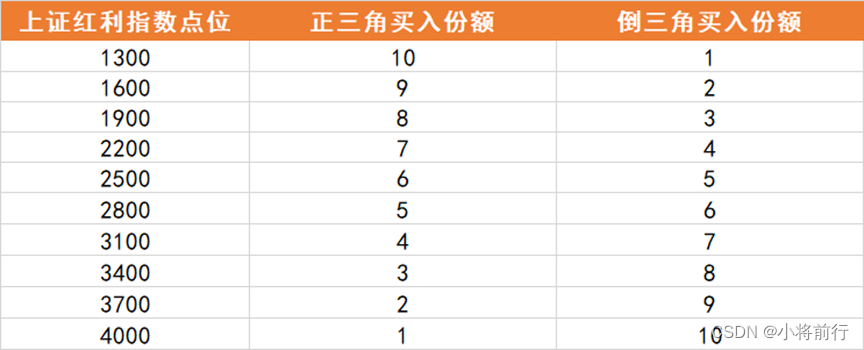
根据定好的模式，来看看正三角和倒三角买入的过程。

下面先给出具体的图例，具体的源码贴在后面，感兴趣大家可以参考。
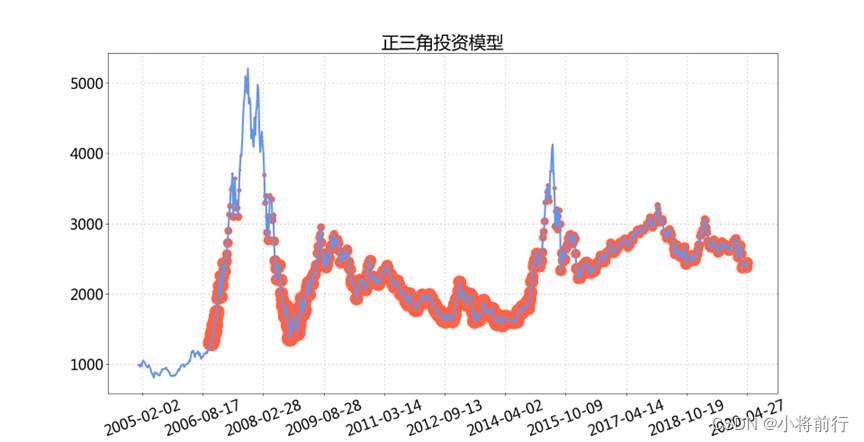
在这里插入图片描述
图中红圈是买入的份额，红圈越大表示买入越多，越小买入越少。可以看出正三角是低位买得多高位买得少，而倒三角正好相反，低位买得少高位买得多。

接着来看看两种方式的投资成本。
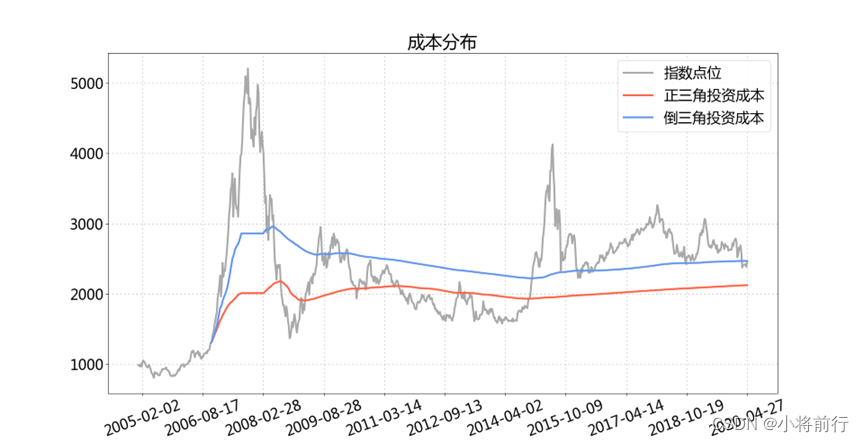
在这里插入图片描述
其中灰色曲线是上证红利的指数点位，很明显的能看出红线（正三角）低于蓝线（倒三角），除了成本低以外，红线（正三角）低于指数点位的区间是比蓝线（倒三角）多的，说明不仅收益高而且回撤小。下面比较下两者的收益走势。
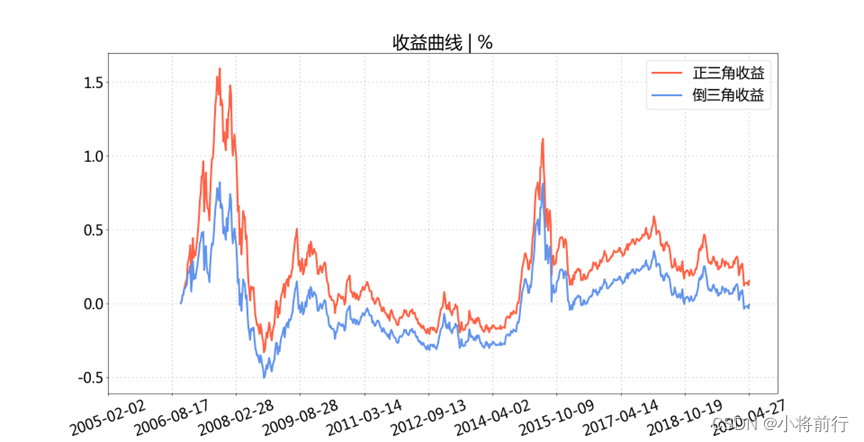
在这里插入图片描述
正三角的投资收益（正收益）在整个投资过程中是100%大于倒三角模式的，而且在某些时间点上会高出几十个百分点，同时回撤（负收益）也更低。

正三角投资是一种有效的投资方式，但真正操作起来却很困难，因为它是反人性的，需要克服周围的干扰和个人情绪的影响，越跌越买需要具备强大的情绪控制能力和极强的耐心。

源码

import pandas as pd
import numpy as np
import math as math
import matplotlib.pyplot as plt

name_index = 'sh.000015'
all_data_index = pd.read_csv('./exportfile/indexDataAll/' + name_index + '.csv')

calc_range = 0
calc_gap = 5
data_index_p = all_data_index['close'].values[0:len(all_data_index['close']):calc_gap]

def triangleDown(val_data_p, buy_cost, invest_count):
    thd_price   = [1300, 1600, 1900, 2200, 2500, 2800, 3100, 3400, 3700, 4000]
    each_invest = [1, 2, 3, 4, 5, 6, 7, 8, 9]
    if thd_price[0] < val_data_p <= thd_price[1]:
        each_ratio_todo = each_invest[0]
    elif thd_price[1] < val_data_p <= thd_price[2]:
        each_ratio_todo = each_invest[1]
    elif thd_price[2] < val_data_p <= thd_price[3]:
        each_ratio_todo = each_invest[2]
    elif thd_price[3] < val_data_p <= thd_price[4]:
        each_ratio_todo = each_invest[3]
    elif thd_price[4] < val_data_p <= thd_price[5]:
        each_ratio_todo = each_invest[4]
    elif thd_price[5] < val_data_p <= thd_price[6]:
        each_ratio_todo = each_invest[5]
    elif thd_price[6] < val_data_p <= thd_price[7]:
        each_ratio_todo = each_invest[6]
    elif thd_price[7] < val_data_p <= thd_price[8]:
        each_ratio_todo = each_invest[7]
    elif thd_price[8] < val_data_p <= thd_price[9]:
        each_ratio_todo = each_invest[8]
    else:
        each_ratio_todo = 0
    buy_each_invest = invest_count * each_ratio_todo
    plot_y = 0
    plot_x = 0
    plot_mark = 0
    if buy_each_invest != 0:
        buy_each_share = buy_each_invest / val_data_p
        buy_cost = buy_cost + buy_each_invest
        plot_y = val_data_p
        plot_x = i
        plot_mark = buy_each_invest
    else:
        buy_each_share = 0

    return buy_each_share, buy_cost, [plot_x, plot_y, plot_mark]

def triangleUp(val_data_p, buy_cost, invest_count):
    thd_price   = [1300, 1600, 1900, 2200, 2500, 2800, 3100, 3400, 3700, 4000]
    each_invest = [9, 8, 7, 6, 5, 4, 3, 2, 1]
    if thd_price[0] < val_data_p <= thd_price[1]:
        each_rati

最低0.47元/天解锁文章