傅里叶级数与傅里叶变换

SongGu1996

已于 2022-10-11 11:17:36 修改

阅读量8.8k

点赞数 25

分类专栏：机器学习文章标签：傅里叶级数傅里叶变换

于 2019-09-03 21:34:44 首次发布

本文链接：https://blog.csdn.net/SongGu1996/article/details/100520730

版权

机器学习专栏收录该内容

13 篇文章

订阅专栏

基础不牢，地动山摇。

傅里叶级数（周期函数）：任何满足狄利克雷收敛条件的周期函数都能用一系列三角函数的和来表示。

傅里叶变换（非周期函数）：傅里叶变换从傅里叶级数变换而来，且傅里叶变换的应用不仅限于周期函数，也适用于非周期函数。

1. 三角函数系的正交性

定义三角函数系为这样一个集合： $\left \{ 1,\ \sin x,\ \cos x,\ \sin 2x,\ \cos 2x,\ \cdots,\ \sin nx,\ \cos nx \right \}$ ；

三角函数系的正交性是指：从三角函数系中任取两个不同的元素，它们的乘积在 $\left [ -\pi,\pi \right ]$ 上的定积分等于零。证明如下图：

2. 周期为“2π”的函数展开为傅里叶级数

设 f(x) 是周期为 $2\pi$ 的周期函数，即： $f(x)=f(x+2\pi)$ 。这样的函数，我们可以将它展开成如下形式：

$f(x)=\sum_{n=0}^{\infty }a_{n}\cos nx+\sum_{n=0}^{\infty }b_{n}\sin nx$

可以看出，在取时，对应着展开式的常数项，让我们将它稍微拆分一下，把常数项单独拎出来：

$f(x)=a_{0}\cos 0x+\sum_{n=1}^{\infty }a_{n}\cos nx+b_{0}\sin 0x+\sum_{n=1}^{\infty }b_{n}\sin nx$

又因为： $\cos 0x=\cos 0=1$ ， $\sin 0x=\sin 0=0$ ，所以展开式可以写成：

$f(x)=a_{0}+\sum_{n=1}^{\infty }a_{n}\cos nx+\sum_{n=1}^{\infty }b_{n}\sin nx$

式中，系数 $a_{0}$ ， $a_{n}$ ， $b_{n}$ 可以用原函数 f(x) 和三角函数表示出来，让我们逐个计算一下：

① 考虑 ${\color{DarkBlue} a_{0}}$

技巧为：对展开式的等号两边同时在 $\left [ -\pi,\pi \right ]$ 上进行积分，计算如下：

$\int_{-\pi}^{\pi}f(x)\ dx=\int_{-\pi}^{\pi}a_{0}\ dx+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }a_{n}\cos nx\ dx+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }b_{n}\sin nx\ dx$

由上面介绍过的三角函数系的正交性可以看出，等号右边第二项和第三项其实都等于零，可以消掉，消掉后运算就变得很简单：

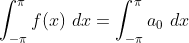
$\int_{-\pi}^{\pi}f(x)\ dx=\int_{-\pi}^{\pi}a_{0}\ dx$

$\int_{-\pi}^{\pi}f(x)\ dx=2\pi\cdot a_{0}$

$a_{0}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\ dx$

② 考虑 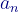${\color{DarkBlue} a_{n}}$

首先，让我们回顾一下 f(x) 的展开式：

$f(x)=a_{0}+\sum_{n=1}^{\infty }a_{n}\cos nx+\sum_{n=1}^{\infty }b_{n}\sin nx$

求 $a_{n}$ 的技巧为：对展开式两边同时先乘一个 $\cos mx$ ，再在 $\left [ -\pi,\pi \right ]$ 上进行积分，计算如下：

$\small \int_{-\pi}^{\pi}f(x)\cos mx\ dx=\int_{-\pi}^{\pi}a_{0}\cos mx\ dx+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }a_{n}\cos nx\cos mx\ dx+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }b_{n}\sin nx\cos mx\ dx$

由上面介绍过的三角函数系的正交性可以看出，等号右边的第一项和第三项其实都等于零，可以消掉，消掉后上式变为：

$\int_{-\pi}^{\pi}f(x)\cos mx\ dx=\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }a_{n}\cos nx\cos mx\ dx$

注意等号的右边，如果我们将求和符号拆开来写，这个式子可以写成：

$\int_{-\pi}^{\pi}f(x)\cos mx\ dx=\int_{-\pi}^{\pi}a_{1}\cos x\cos mx\ dx+\int_{-\pi}^{\pi}a_{2}\cos 2x\cos mx\ dx+\cdots+{\color{Red} \int_{-\pi}^{\pi}a_{m}\cos mx\cos mx\ dx}+\int_{-\pi}^{\pi}a_{n}\cos nx\cos mx\ dx$

由三角函数系的正交性可以看出，等号右边的无穷项中大部分都为零，只有一项不是零，这一项已经在上式中标红，因为三角函数系中两个不同的元素相乘才具有正交性，而这一项中的两个元素是相同的。将式子中等于零的项都去掉，可得：

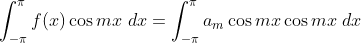
$\int_{-\pi}^{\pi}f(x)\cos mx\ dx=\int_{-\pi}^{\pi}a_{m}\cos mx\cos mx\ dx$
$=a_{m}\int_{-\pi}^{\pi}\cos ^{2}mx\ dx=a_{m}\int_{-\pi}^{\pi}\frac{1+\cos 2mx}{2}\ dx=a_{m}\int_{-\pi}^{\pi}\frac{1}{2}\ dx+a_{m}\int_{-\pi}^{\pi}\frac{\cos 2mx}{2}\ dx$
$=\pi\cdot a_{m}$

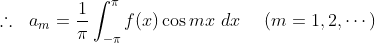
$\therefore \ \ a_{m}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos mx\ dx\ \ \ \ (m=1,2,\cdots)$

将换成即可得到 $a_{n}$ 的表达式：

$a_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\ dx\ \ \ \ (n=1,2,\cdots)$

③ 考虑 ${\color{DarkBlue} b_{n}}$

首先，还是先回顾一下 f(x) 的展开式：

$f(x)=a_{0}+\sum_{n=1}^{\infty }a_{n}\cos nx+\sum_{n=1}^{\infty }b_{n}\sin nx$

求 $b_{n}$ 的技巧为：对展开式两边同时先乘一个 $\sin mx$ ，再在 $\left [ -\pi,\pi \right ]$ 上进行积分，计算如下：

$\small \int_{-\pi}^{\pi}f(x)\sin mx\ dx=\int_{-\pi}^{\pi}a_{0}\sin mx\ dx+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }a_{n}\cos nx\sin mx\ dx+\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }b_{n}\sin nx\sin mx\ dx$

由三角函数系的正交性可以看出，等号右边第一项和第二项其实都等于零，可以消掉，消掉后上式变为：

$\small \int_{-\pi}^{\pi}f(x)\sin mx\ dx=\int_{-\pi}^{\pi}\sum_{n=1}^{\infty }b_{n}\sin nx\sin mx\ dx$

接下来的思路与算 $a_{n}$ 时一样，不再赘述，最后求得 $b_{n}$ 的表达式为：

$b_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx\ dx\ \ \ \ (n=1,2,\cdots)$

综上所述，周期为 $2\pi$ 的函数 f(x) 的傅里叶展开式为：

$f(x)=a_{0}+\sum_{n=1}^{\infty }a_{n}\cos nx+\sum_{n=1}^{\infty }b_{n}\sin nx$
$a_{0}=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)\ dx$
$a_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\ dx\ \ \ \ (n=1,2,\cdots)$
$b_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx\ dx\ \ \ \ (n=1,2,\cdots)$

但是我们发现， $a_{0}$ 的表达式中，系数为 $1/2\pi$ ，而 $a_{n}$ 和 $b_{n}$ 的表达式中，系数都为 $1/\pi$ ，为了照顾强迫症患者，周期为 $2\pi$ 的函数 f(x) 的傅里叶展开式还有另一种写法，同时这也是课本中广泛使用的写法：

${\color{DarkRed} f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }a_{n}\cos nx+\sum_{n=1}^{\infty }b_{n}\sin nx}$
${\color{DarkRed} a_{0}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\ dx}$
${\color{DarkRed} a_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nx\ dx\ \ \ \ (n=1,2,\cdots)}$
${\color{DarkRed} b_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nx\ dx\ \ \ \ (n=1,2,\cdots)}$

3. 周期为“2L”的函数展开为傅里叶级数

让我们将傅里叶级数推广到更一般的情况，假设 f(x) 是周期为的周期函数，即： f(x)=f(x+2L) 。在这里，我们的技巧是用换元法将这个周期为的函数转化成一个周期为 $2\pi$ 的新函数。思路如下：首先，考虑 $-L\leq x\leq L$ 是函数 f(x) 的一个周期，如果我们对这个周期同时除以，再同时乘上 $\pi$ ，可以转化为：

$-L\leq x\leq L\ \ \ \rightarrow \ \ \ -1\leq \frac{x}{L}\leq 1 \ \ \ \rightarrow \ \ \ -\pi\leq \frac{\pi x}{L}\leq \pi$

作变量代换 $z=\frac{\pi x}{L}$ ，于是我们就将区间 $-L\leq x\leq L$ 变换成了 $-\pi\leq z\leq \pi$ 。

由 $z=\frac{\pi x}{L}$ 可以得到 $x=\frac{Lz}{\pi}$ ，我们令： $f(x)=f(\frac{Lz}{\pi})=F(z)$ ，可以证明 F(z) 是周期为 $2\pi$ 的周期函数：

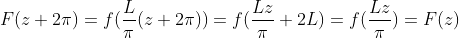
$F(z+2\pi)=f(\frac{L}{\pi}(z+2\pi))=f(\frac{Lz}{\pi}+2L)=f(\frac{Lz}{\pi})=F(z)$

所以我们可以将 F(z) 展开为傅里叶级数：

$F(z)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }a_{n}\cos nz+\sum_{n=1}^{\infty }b_{n}\sin nz$
$a_{0}=\frac{1}{\pi}\int_{-\pi}^{\pi}F(z)\ dz$
$a_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}F(z)\cos nz\ dz\ \ \ \ (n=1,2,\cdots)$
$b_{n}=\frac{1}{\pi}\int_{-\pi}^{\pi}F(z)\sin nz\ dz\ \ \ \ (n=1,2,\cdots)$

在以上式子中令： $z=\frac{\pi x}{L}$ ，并且注意到 F(z)=f(x) ，于是可以得到周期为的函数 f(x) 的傅里叶级数：

${\color{DarkRed} f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }a_{n}\cos \frac{n\pi x}{L}+\sum_{n=1}^{\infty }b_{n}\sin \frac{n\pi x}{L}}$
${\color{DarkRed} a_{0}=\frac{1}{L}\int_{-L}^{L}f(x)\ dx}$
${\color{DarkRed} a_{n}=\frac{1}{L}\int_{-L}^{L}f(x)\cos \frac{n\pi x}{L}\ dx\ \ \ \ (n=1,2,\cdots)}$
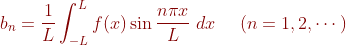
${\color{DarkRed} b_{n}=\frac{1}{L}\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L}\ dx\ \ \ \ (n=1,2,\cdots)}$

4. 傅里叶级数的复数形式

傅里叶级数还可以用复数形式表示，这里我们需要借助欧拉公式：

$\cos t=\frac{1}{2}(e^{it}+e^{-it})\ \ ,\ \ \sin t=-\frac{1}{2}i(e^{it}-e^{-it})$

利用欧拉公式可以将上面周期为的函数的傅里叶级数进行转化：

$f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }(a_{n}\cos \frac{n\pi x}{L}+b_{n}\sin \frac{n\pi x}{L})$
$=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }\left [ \frac{a_{n}}{2}(e^{\frac{n\pi x}{L}i}+e^{-\frac{n\pi x}{L}i})-\frac{b_{n}}{2}i(e^{\frac{n\pi x}{L}i}-e^{-\frac{n\pi x}{L}i}) \right ]$
$=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }\left [ \frac{a_{n}-b_{n}i}{2}e^{\frac{n\pi x}{L}i}+\frac{a_{n}+b_{n}i}{2}e^{-\frac{n\pi x}{L}i} \right ]$
$=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }\frac{a_{n}-b_{n}i}{2}e^{\frac{n\pi x}{L}i}+\sum_{n=1}^{\infty }\frac{a_{n}+b_{n}i}{2}e^{-\frac{n\pi x}{L}i}$

将等号右边第三项中的""用""来替换，即：

$\sum_{n=1}^{\infty }\frac{a_{n}+b_{n}i}{2}e^{-\frac{n\pi x}{L}i}=\sum_{n=-\infty }^{-1}\frac{a_{-n}+b_{-n}i}{2}e^{\frac{n\pi x}{L}i}$

大家可能有疑问，真的可以这样替换吗？答案是可以的，如果我们将求和符号拆开来写，会发现等号两边是同样的元素在相加。

可以发现，等号右边第二项和第三项都含有 $e^{\frac{n\pi x}{L}i}$ ，让我们将等号右边第一项改写一下，让它也含有 $e^{\frac{n\pi x}{L}i}$ ：

$\frac{a_{0}}{2}=\sum_{n=0}^{0}\frac{a_{0}}{2}e^{\frac{n\pi x}{L}i}$

由于 n=0 ，所以这一项中 $e^{\frac{n\pi x}{L}i}$ 其实等于；把等号右边第一项和第三项这样处理一下之后，复数形式的展开可以变为：

$f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }\frac{a_{n}-b_{n}i}{2}e^{\frac{n\pi x}{L}i}+\sum_{n=1}^{\infty }\frac{a_{n}+b_{n}i}{2}e^{-\frac{n\pi x}{L}i}$
$=\sum_{n=0}^{0}\frac{a_{0}}{2}e^{\frac{n\pi x}{L}i}+\sum_{n=1}^{\infty }\frac{a_{n}-b_{n}i}{2}e^{\frac{n\pi x}{L}i}+\sum_{n=-\infty }^{-1}\frac{a_{-n}+b_{-n}i}{2}e^{\frac{n\pi x}{L}i}$

写成这样之后，我们发现，已经包含了从 $-\infty$ 到 $\infty$ 的所有整数，所以，我们将展开式进一步简写为：

$f(x)=\sum_{-\infty }^{\infty }C_{n}e^{\frac{n\pi x}{L}i}$
$C_{n}=\left\{\begin{matrix} \frac{a_0}{2} & n=0\\ \frac{a_{n}-b_{n}i}{2}& \ \ \ \ \ \ n=1,2,3,4,\cdots\cdots\\ \frac{a_{-n}+b_{-n}i}{2}& \ \ \ \ n=-1,-2,-3,-4,\cdots\cdots\end{matrix}\right.$

将上一节最后得到的 $a_{0}$ ， $a_{n}$ ， $b_{n}$ 的值代入，可以得到：

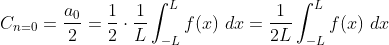
$C_{n=0}=\frac{a_{0}}{2}=\frac{1}{2}\cdot \frac{1}{L}\int_{-L}^{L}f(x)\ dx=\frac{1}{2L}\int_{-L}^{L}f(x)\ dx$

$C_{n=1,2,3,\cdots}=\frac{a_{n}-b_{n}i}{2}=\frac{1}{2}\left [ \frac{1}{L}\int_{-L}^{L}f(x)\cos \frac{n\pi x}{L}\ dx -\frac{1}{L}\cdot i\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L}\ dx\right ]=\frac{1}{2L}\int_{-L}^{L}f(x)\cdot (\cos \frac{n\pi x}{L}-i\cdot\sin \frac{n\pi x}{L})=\frac{1}{2L}\int_{-L}^{L}f(x)\cdot e^{-i\cdot\frac{n\pi x}{L}}dx$

$C_{n=-1,-2,-3,\cdots}=\frac{a_{-n}+b_{-n}i}{2}=\frac{1}{2}\left [ \frac{1}{L}\int_{-L}^{L}f(x)\cos \frac{-n\pi x}{L}\ dx +\frac{1}{L}\cdot i\int_{-L}^{L}f(x)\sin \frac{-n\pi x}{L}\ dx\right ]=\frac{1}{2L}\int_{-L}^{L}f(x)\cdot (\cos \frac{-n\pi x}{L}+i\cdot\sin \frac{-n\pi x}{L})=\frac{1}{2L}\int_{-L}^{L}f(x)\cdot (\cos \frac{n\pi x}{L}-i\cdot\sin \frac{n\pi x}{L})=\frac{1}{2L}\int_{-L}^{L}f(x)\cdot e^{-i\cdot\frac{n\pi x}{L}}dx$

到这一步，我们惊喜地发现，在取正整数或者负整数时， $C_{n}$ 的表达式是一样的，其实可以在取时，这个表达式同样成立，即我们可以只用这一个式子将所有的系数表示出来。那么周期为的函数展开成傅里叶级数的复数形式可以表示为：

${\color{DarkRed} f(x)=\sum_{-\infty }^{\infty }C_{n}e^{\frac{n\pi x}{L}i}}$
${\color{DarkRed} C_{n}=\frac{1}{2L}\int_{-L}^{L}f(x)\cdot e^{-i\cdot\frac{n\pi x}{L}}dx}$

5. 傅里叶变换

在实际应用中，我们会用一些符号使得式子看起来更舒服一些，我们用来表示周期，即 T=2L ；再令 $w_{0}=\frac{2\pi}{T}=\frac{\pi}{L}$ ，我们称 $w_{0}$ 为基频率，将这些符号表达加入后，周期为的函数的傅里叶级数可以写为：

$f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty }a_{n}\cos \frac{n\pi x}{L}+\sum_{n=1}^{\infty }b_{n}\sin \frac{n\pi x}{L}={\color{DarkBlue} \frac{a_{0}}{2}+\sum_{n=1}^{\infty }a_{n}\cos nw_{0}x+\sum_{n=1}^{\infty }b_{n}\sin nw_{0}x}$
$a_{0}=\frac{1}{L}\int_{-L}^{L}f(x)\ dx={\color{DarkBlue} \frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)\ dx}$
$a_{n}=\frac{1}{L}\int_{-L}^{L}f(x)\cos \frac{n\pi x}{L}\ dx={\color{DarkBlue} \frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)\cos nw_{0}x\ dx}$
$b_{n}=\frac{1}{L}\int_{-L}^{L}f(x)\sin \frac{n\pi x}{L}\ dx={\color{DarkBlue} \frac{2}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)\sin nw_{0}x\ dx}$

周期为的函数傅里叶级数的复数形式可以表示为：

$f(x)=\sum_{-\infty }^{\infty }C_{n}e^{\frac{n\pi x}{L}i}={\color{DarkBlue} \sum_{-\infty }^{\infty }C_{n}e^{i\cdot nw_{0}x}}$
$C_{n}=\frac{1}{2L}\int_{-L}^{L}f(x)\cdot e^{-i\cdot\frac{n\pi x}{L}}dx={\color{DarkBlue} \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)\cdot e^{-i\cdot nw_{0}x}\ dx}$

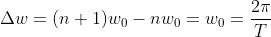前面讨论的都是周期函数，那么非周期函数怎么办呢，能否找到一种更加一般的表达形式呢？非周期函数，顾名思义，它不会重复，或者说在无穷远处会重复，所以我们可以认为非周期函数的周期 $T\rightarrow \infty$ ，此时， $w_{0}=\frac{2\pi}{T}\rightarrow 0$ 。让我们以 $nw_{0}$ 为变量，当 $w_{0}\neq 0$ 时， $nw_{0}$ 是离散值，当 $w_{0}$ 趋近于无穷小时，它就成为连续变量，取为，那么 $\Delta w=(n+1)w_{0}-nw_{0}=w_{0}=\frac{2\pi}{T}$ ； $\frac{1}{T}=\frac{\Delta w}{2\pi}$ ，让我们先将 $C_{n}$ 代入 f(x) 写成完整形式：

$f(x)=\sum_{-\infty }^{\infty }C_{n}e^{i\cdot nw_{0}x}=\sum_{-\infty }^{\infty } \frac{1}{T}\int_{-\frac{T}{2}}^{\frac{T}{2}}f(x)\cdot e^{-i\cdot nw_{0}x}\ dx\cdot e^{i\cdot nw_{0}x}$