状态空间方程

什么是状态方程？

一个动态系统可以用常微分方程表示，这是因为动态系统拥有其在任何时候的变化都是其当前状态的函数的特性。

以一个弹簧质量系统为例，

我们可以很容易推导出其微分方程：

从上述微分方程可以看出，系统的加速度是当前状态（位置）的方程，如果这一动态系统有初始能量，因为其状态和状态导数之间存在关系，它会一直持续运动。如果将弹簧拉伸后放开，它的加速度会改变速度进而改变位置，从而再次影响加速度。在上述系统中没有阻尼，能量未被消耗，其加速度->速度->位置循环会一直持续，使质量块即使在没有外力影响时也会一直做往复运动。

如果我们通过分析系统的状态和其状态导数之间的关系来看能量变化，我们可以对系统的稳定性做出这样的判断：如果能量随着时间的推移而耗散，那么系统就是稳定的。而如果能量耗散得越快，那么系统就越稳定。如果能量随着时间的推移而无限制地增长，哪怕只是其中的一部分，那么整个系统就是不稳定的。

稳定是一个系统的固有属性，它仅仅来自于状态及其导数之间的相互联系。然而，随着时间的推移，系统运动的方式也会受到外部能量增减的影响。因此，动态系统的导数既是当前状态的函数，也是任何外部输入的函数。

而状态空间表示法只不过是将高阶微分方程重新打包成一组一阶微分方程。这种重新包装可以使系统更易于分析，因为我们可以查看相互关联系统的基本行为，以及系统如何受到外部输入（甚至是多个外部输入）的影响。

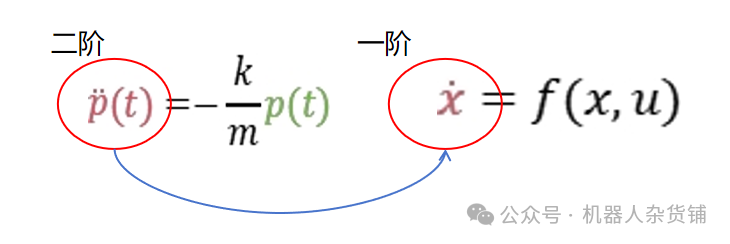
还有很多控制技术都建立在状态空间模型的基础上，如卡尔曼滤波、LQR 控制、鲁棒控制和模型预测控制等。在将系统用状态空间模型表述时，由于首先要建立导数向量，然后对整个向量进行积分以获得状态，因此在数值求解方面也有优势。

状态空间方程有两个方程：第一个是状态方程，第二个是输出方程。

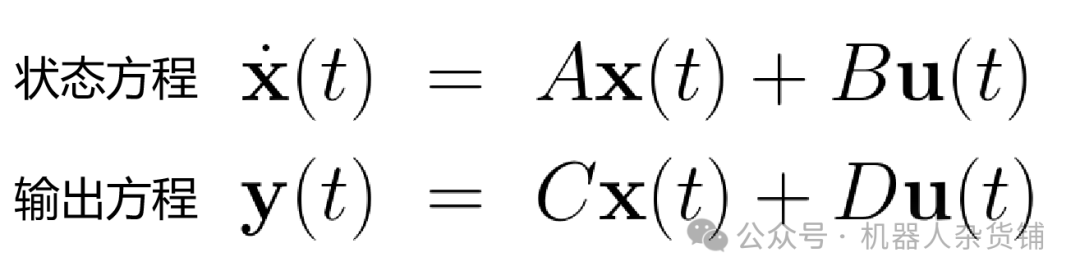
状态空间表示法是围绕状态向量 x 建立的。状态向量的变化或状态向量的导数，是当前状态加上外部输入的线性组合。

这样，我们就不用像使用高阶微分方程或传递函数那样，从头到尾观察系统的整个动态变化，而是专注于每个状态变量的动态变化，以及这些变量之间的关系。

状态方程的矩阵形式有两个矩阵，A 和 B。A 矩阵描述了内部状态如何相互关联，即系统的基本动态；B 矩阵描述了输入如何进入系统--它们会影响哪些状态？

现在我们来看看输出方程。Y 是系统输出的矢量。需要注意的是，输出并不一定就是状态变量。C 矩阵描述了如何将状态组合起来以获得输出，而 D 矩阵则用于让输入完全绕过系统并前馈到输出。

D 矩阵在实际应用中的简单例子是一个简单乘法器的状态空间表示，即增益块。输出等于输入乘以增益，因此在这种情况下，由于没有导数和状态，A、B 和 C 矩阵都为 0，而 D 矩阵就是增益值。

---

什么是状态变量？

状态变量是整个状态方程的关键，那么，怎么理解状态变量呢？

状态变量是完整描述系统的最小变量集合。完整描述的意思是：这一集合包含足够的信息，可以预测系统的未来行为。

再回到前面提到的弹簧-质量系统，在不了解系统信息的情况下，找出系统的状态变量，这将更有意义。如果要预测系统在一秒钟后的位置，都需要哪些信息？

首先需要弹簧常数k和质量m等系统常量，此外还需要知道作用在质量上的外力是什么，因此需要输入u。

但这只能获取部分信息，因为系统变量部分的初始条件还未知。这包括：

• • 质量块目前是否在移动？

  • 弹簧目前对质量的拉力有多大？

如果我们知道了这两个初始条件，再加上系统常量和输入，我们就能预测出一秒钟后质量的位置。

那么我们来考虑第一个问题：质量块目前是否在移动？假设这个系统中存在一些能量，那么质量块会往复运动，我们可以通过质量块的速度来判断质量块是否在移动。我们需要速度来预测未来的位置，因此我们可以说它是必要的，可以作为一个状态变量。

现在我们再看看初始弹簧力。力也是可变的，但是要如何获取呢？它是弹簧常数乘以弹簧拉伸的距离。

弹簧力 = k * 距离

因此，如果我们有了这个距离，或者质量块相对于未拉伸弹簧长度的位置，就能得到弹簧力。

因此，要完全描述这个系统，我们至少需要两个变量：位置和速度。既然有两个变量，这就是一个二阶系统。

那么问题又来了：为什么不是更多的状态呢？为什么不是三个？

要回答这个问题，让我们来考虑加速度。加速度是一个变量，因为它随着位置和速度的变化而变化。然而，我们并不需要知道加速度就能完全描述系统；加速度是作用在质量块上的力的结果，而在这种情况下，力是质量块位置的副产品。因此，我们通过位置获得加速度，而在状态变量列表中增加加速度是冗余信息。

初看起来可能有些奇怪的是，如果我们在这个系统中添加一个阻尼器，我们并没有增加这个系统的阶次，因为我们不需要任何额外的状态变量来解释这个额外的元素。阻尼器产生的力由质量的速度决定，而质量的速度已经包含在我们的状态变量列表中。因此，这两个系统的状态变量数量都是两个：位置和速度。

能不能是另两个不同的状态？

如果状态必须是两个，那为什么不是另两个不同的状态？为什么是位置和速度？其实，不一定非得位置和速度这两个状态变量。位置和速度这两个状态变量可以看作是状态空间中的坐标系。

但我们可以用任意两个线性独立变量来描述状态空间中的这个位置。任意的状态 1 和状态 2。我们最终会得到相同的系统状态、相同的总能量，只是坐标不同而已。

在状态空间表示法中，我们经常对状态变量进行重新定义。仍以上述弹簧阻尼系统举例，当我们将其 A 矩阵对角化，使其成为所谓的模态形式，便是在重定义状态变量。

这两个模型表示的是完全相同的系统，我们只是为状态向量选择了不同的坐标，不同的基础。因此，状态向量 x 由位置和速度组成，而状态向量 z 则由两个模态组成，这些特定状态的变化仅仅是它们自身的函数。也就是说，状态 1 并不依赖于状态 2 的当前值，反之亦然。如果我们能直接以模态形式写出状态空间表示，也许就能写出了。对于状态变量来说，位置和速度并没有什么特别之处，只是它们对我们来说是直观意义上的量。

不过，由于状态不再定义为位置和速度，如果我们想将系统的输出保持为位置和速度，C 矩阵也需要改变。通过这种方式，我们可以看到输出方程的好处。我们不必被迫完全按照我们的定义输出状态，而是能够将它们线性组合成我们感兴趣的变量。

与其把状态空间方程看作是将模型重新打包成任意一阶微分方程的一组矩阵，我们可以把它们看作是分别写出每个状态变量的动力学。而动态变化与能量在系统中的存储和传输方式息息相关。这样做的好处是，我们能够了解这些内部状态是如何变化和相互关联的，能量是如何移动的，我们还能使用线性代数的强大工具来分析和求解方程。

下次分享将会用matlab给出具体实例，以更深入了解状态空间方程。

也可关注公众号“机器人杂货铺”，发现更多精彩内容