深度学习 10 — Pytorch 实现车牌识别

TOMWilliamLIN

已于 2024-05-17 15:11:48 修改

阅读量1.3k

点赞数 12

分类专栏：深度学习文章标签：深度学习 pytorch 人工智能

于 2024-05-17 15:09:34 首次发布

本文链接：https://blog.csdn.net/TOMWilliamLIN/article/details/138858220

版权

深度学习专栏收录该内容

11 篇文章

订阅专栏

🍨 本文为[🔗365天深度学习训练营]中的学习记录博客

🍖 原作者：[K同学啊]

一、导入数据

import torch.nn as nn
import torch, torchvision
import torchvision.models as models
import torch.nn.functional as F
from torchvision import datasets
from torch.utils.data import DataLoader
from torchvision.transforms import transforms
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
device

1.获取类别名

import os, PIL, random, pathlib
import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif'] = ['SimHei'];
plt.rcParams['axes.unicode_minus'] = False;

data_dir = "./data"
data_dir = pathlib.Path(data_dir)

data_paths = list(data_dir.glob('*'))
classeNames = [str(path).split("/")[1].split("_")[1].split(".")[0] for path in data_paths]
print(classeNames)

data_paths = list(data_dir.glob('*'))
data_paths_str = [str(path) for path in data_paths]

data_paths_str

2.数据可视化

3.标签数字化

import numpy as np
char_enum = ["京","沪","津","渝","冀","晋","蒙","辽","吉","黑","苏","浙","皖","闽","赣","鲁",\
              "豫","鄂","湘","粤","桂","琼","川","贵","云","藏","陕","甘","青","宁","新","军","使"]
number = [str(i) for i in range(0,10)]
alphabet = [chr(i) for i in range(65,91)]

char_set = char_enum + number + alphabet
char_set_len = len(char_set)
label_name_len = len(classeNames[0])


def text2vec(text):
    vector = np.zeros([label_name_len,char_set_len])

    for i, c in enumerate(text):
        idx = char_set.index(c)
        vector[i][idx] = 1.0
    return vector

all_labels = [text2vec(i) for i in classeNames]

4.加载数据文件

import os
import pandas as pd
from PIL import Image

import torch.utils.data as data 
from torch.utils.data import Dataset
from torchvision.io import read_image

class MyDataset(data.Dataset):
    def __init__(self, all_labels, data_paths_str, transform):
        self.img_labels = all_labels
        self.img_dir = data_paths_str
        self.transform = transform

    def __len__(self):
        return len(self.img_labels)
    
    def __getitem__(self, index):
        image = Image.open(self.img_dir[index]).convert('RGB')
        label = self.img_labels[index]
        
        if self.transform:
            image = self.transform(image)
        return image, label

total_datadir = "./data"

train_transforms = transforms.Compose([
    transforms.Resize([224,224]),
    transforms.ToTensor(),
    transforms.Normalize(
        mean = [0.485, 0.456,0.406],
        std = [0.229, 0.224, 0.225])
])

total_data = MyDataset(all_labels, data_paths_str, train_transforms)
total_data

5.数据划分

train_size = int(0.8 * len(total_data))
test_size = len(total_data) - train_size

train_dataset, test_dataset = torch.utils.data.random_split(total_data, [train_size,test_size])

train_size, test_size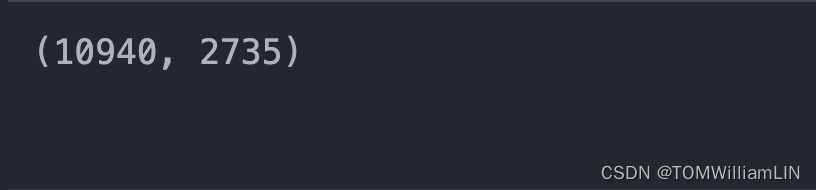

train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=16,shuffle=True)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=16,shuffle=True)

print("The number of images in a training set is: ", len(train_loader)*16)
print("The number of images in a test set is: ", len(test_loader)*16)
print("The number of batches per epoch is: ", len(train_loader))

for X, y in test_loader:
    print("Shape of X [N, C, H, W]: ", X.shape);
    print("Shape of y: ", y.shape, y.dtype);
    break;

二、自建模型

class Network_bn(nn.Module):
    def __init__(self):
        super(Network_bn, self).__init__()
        self.conv1 = nn.Conv2d(in_channels=3, out_channels=12, kernel_size=5, stride=1, padding=0)
        self.bn1 = nn.BatchNorm2d(12)
        self.conv2 = nn.Conv2d(in_channels=12, out_channels=12, kernel_size=5, stride=1, padding=0)
        self.bn2 = nn.BatchNorm2d(12)
        self.pool = nn.MaxPool2d(2,2)
        self.conv4 = nn.Conv2d(in_channels=12, out_channels=24, kernel_size=5, stride=1, padding=0)
        self.bn4 = nn.BatchNorm2d(24)
        self.conv5 = nn.Conv2d(in_channels=24, out_channels=24, kernel_size=5, stride=1, padding=0)
        self.bn5 = nn.BatchNorm2d(24)
        self.fc1 = nn.Linear(24*50*50, label_name_len*char_set_len)
        self.reshape = Reshape([label_name_len,char_set_len])

    def forward(self, x):
        x = F.relu(self.bn1(self.conv1(x)))
        x = F.relu(self.bn2(self.conv2(x)))
        x = self.pool(x)
        x = F.relu(self.bn4(self.conv4(x)))
        x = F.relu(self.bn5(self.conv5(x)))
        x = self.pool(x)
        x = x.view(-1, 24*50*50)
        x = self.fc1(x)

        x = self.reshape(x)

        return x

class Reshape(nn.Module):
    def __init__(self, shape):
        super(Reshape, self).__init__()
        self.shape = shape

    def forward(self, x):
        return x.view(x.size(0),*self.shape)

device = "cuda" if torch.cuda.is_available() else "cpu"

print("Using {} device".format(device))
model = Network_bn().to(device)
model

import torchsummary

torchsummary.summary(model, (3,224,224))

三、模型训练

1. 优化器和损失函数

optimizer = torch.optim.Adam(model.parameters(),lr=1e-4,weight_decay=0.0001)

loss_model = nn.CrossEntropyLoss()

from torch.autograd import Variable
def test(model, test_loader, loss_model):
    size = len(test_loader.dataset) 
    num_batches = len(test_loader)
   
    model.eval()
    test_loss, correct = 0, 0
    with torch.no_grad():
        for X, y in test_loader:
            X, y = X.to(device), y.to(device)
            pred = model(X)
            

            test_loss += loss_model(pred, y).item()
                  
            pred = pred.argmax(2)
            _, predicted = torch.max(y, 2)
            correct += (pred == predicted).type(torch.float).sum().item()/(y.size(0)*y.size(1))

    test_loss /= num_batches
    correct /= num_batches
 
    print(f'Avg loss: {test_loss:>8f}, accuracy:{correct:>8f}\n')
    return correct, test_loss
 
 
def train(model,train_loader, loss_model, optimizer):
    size = len(train_loader.dataset)
    num_batches = len(train_loader)
    model = model.to(device)
    model.train()
 
    for i, (images, labels) in enumerate(train_loader, 0):   # 0 是标起始位置的值
        images = Variable(images.to(device))
        labels = Variable(labels.to(device))
 
        optimizer.zero_grad()
        outputs = model(images)

        loss = loss_model(outputs, labels)
        loss.backward()
        optimizer.step()
 
        if i % 100 == 0:
            print('[%5d] loss: %.3f' % (i, loss))

2.模型训练

test_acc_list  = []
test_loss_list = []
epochs = 30

for t in range(epochs):
    print(f"Epoch {t+1}\n-------------------------------")
    train(model,train_loader,loss_model,optimizer)
    test_acc,test_loss = test(model, test_loader, loss_model)
    test_acc_list.append(test_acc)
    test_loss_list.append(test_loss)
print("Done!")

Epoch 1
-------------------------------
[    0] loss: 0.211
[  100] loss: 0.163
[  200] loss: 0.141
[  300] loss: 0.125
[  400] loss: 0.090
[  500] loss: 0.090
[  600] loss: 0.097
Avg loss: 0.072495, accuracy:0.312023

Epoch 2
-------------------------------
[    0] loss: 0.061
[  100] loss: 0.055
[  200] loss: 0.049
[  300] loss: 0.057
[  400] loss: 0.066
[  500] loss: 0.052
[  600] loss: 0.054
Avg loss: 0.054252, accuracy:0.391830

Epoch 3
-------------------------------
[    0] loss: 0.032
[  100] loss: 0.022
[  200] loss: 0.027
[  300] loss: 0.046
[  400] loss: 0.020
[  500] loss: 0.033
[  600] loss: 0.025
Avg loss: 0.046970, accuracy:0.445750

Epoch 4
-------------------------------
[    0] loss: 0.027
[  100] loss: 0.018
[  200] loss: 0.039
[  300] loss: 0.041
[  400] loss: 0.026
[  500] loss: 0.022
[  600] loss: 0.027
Avg loss: 0.045500, accuracy:0.476375

Epoch 5
-------------------------------
[    0] loss: 0.015
[  100] loss: 0.016
[  200] loss: 0.019
[  300] loss: 0.024
[  400] loss: 0.024
[  500] loss: 0.033
[  600] loss: 0.020
Avg loss: 0.041513, accuracy:0.496481

Epoch 6
-------------------------------
[    0] loss: 0.030
[  100] loss: 0.016
[  200] loss: 0.021
[  300] loss: 0.011
[  400] loss: 0.023
[  500] loss: 0.036
[  600] loss: 0.013
Avg loss: 0.039971, accuracy:0.512403

Epoch 7
-------------------------------
[    0] loss: 0.032
[  100] loss: 0.021
[  200] loss: 0.014
[  300] loss: 0.024
[  400] loss: 0.024
[  500] loss: 0.010
[  600] loss: 0.020
Avg loss: 0.037215, accuracy:0.525355

Epoch 8
-------------------------------
[    0] loss: 0.018
[  100] loss: 0.010
[  200] loss: 0.021
[  300] loss: 0.014
[  400] loss: 0.015
[  500] loss: 0.019
[  600] loss: 0.033
Avg loss: 0.036857, accuracy:0.527061

Epoch 9
-------------------------------
[    0] loss: 0.029
[  100] loss: 0.008
[  200] loss: 0.032
[  300] loss: 0.023
[  400] loss: 0.015
[  500] loss: 0.021
[  600] loss: 0.018
Avg loss: 0.036141, accuracy:0.538019

Epoch 10
-------------------------------
[    0] loss: 0.020
[  100] loss: 0.024
[  200] loss: 0.010
[  300] loss: 0.013
[  400] loss: 0.023
[  500] loss: 0.021
[  600] loss: 0.012
Avg loss: 0.035489, accuracy:0.550773

Epoch 11
-------------------------------
[    0] loss: 0.013
[  100] loss: 0.011
[  200] loss: 0.021
[  300] loss: 0.011
[  400] loss: 0.014
[  500] loss: 0.012
[  600] loss: 0.013
Avg loss: 0.034673, accuracy:0.552903

Epoch 12
-------------------------------
[    0] loss: 0.018
[  100] loss: 0.013
[  200] loss: 0.013
[  300] loss: 0.010
[  400] loss: 0.008
[  500] loss: 0.027
[  600] loss: 0.013
Avg loss: 0.032326, accuracy:0.570826

Epoch 13
-------------------------------
[    0] loss: 0.026
[  100] loss: 0.020
[  200] loss: 0.019
[  300] loss: 0.015
[  400] loss: 0.015
[  500] loss: 0.020
[  600] loss: 0.016
Avg loss: 0.033008, accuracy:0.565577

Epoch 14
-------------------------------
[    0] loss: 0.016
[  100] loss: 0.021
[  200] loss: 0.024
[  300] loss: 0.019
[  400] loss: 0.018
[  500] loss: 0.018
[  600] loss: 0.016
Avg loss: 0.032402, accuracy:0.578947

Epoch 15
-------------------------------
[    0] loss: 0.017
[  100] loss: 0.021
[  200] loss: 0.021
[  300] loss: 0.016
[  400] loss: 0.010
[  500] loss: 0.015
[  600] loss: 0.019
Avg loss: 0.031984, accuracy:0.579306

Epoch 16
-------------------------------
[    0] loss: 0.024
[  100] loss: 0.017
[  200] loss: 0.018
[  300] loss: 0.016
[  400] loss: 0.017
[  500] loss: 0.023
[  600] loss: 0.009
Avg loss: 0.031577, accuracy:0.587361

Epoch 17
-------------------------------
[    0] loss: 0.010
[  100] loss: 0.012
[  200] loss: 0.015
[  300] loss: 0.013
[  400] loss: 0.016
[  500] loss: 0.021
[  600] loss: 0.011
Avg loss: 0.030837, accuracy:0.593679

Epoch 18
-------------------------------
[    0] loss: 0.015
[  100] loss: 0.016
[  200] loss: 0.016
[  300] loss: 0.008
[  400] loss: 0.013
[  500] loss: 0.026
[  600] loss: 0.013
Avg loss: 0.029765, accuracy:0.600233

Epoch 19
-------------------------------
[    0] loss: 0.013
[  100] loss: 0.015
[  200] loss: 0.011
[  300] loss: 0.025
[  400] loss: 0.027
[  500] loss: 0.009
[  600] loss: 0.018
Avg loss: 0.029967, accuracy:0.599154

Epoch 20
-------------------------------
[    0] loss: 0.020
[  100] loss: 0.013
[  200] loss: 0.018
[  300] loss: 0.010
[  400] loss: 0.013
[  500] loss: 0.012
[  600] loss: 0.009
Avg loss: 0.030177, accuracy:0.596397

Epoch 21
-------------------------------
[    0] loss: 0.021
[  100] loss: 0.006
[  200] loss: 0.005
[  300] loss: 0.006
[  400] loss: 0.025
[  500] loss: 0.013
[  600] loss: 0.011
Avg loss: 0.028662, accuracy:0.611160

Epoch 22
-------------------------------
[    0] loss: 0.017
[  100] loss: 0.017
[  200] loss: 0.018
[  300] loss: 0.019
[  400] loss: 0.009
[  500] loss: 0.011
[  600] loss: 0.013
Avg loss: 0.028990, accuracy:0.611821

Epoch 23
-------------------------------
[    0] loss: 0.015
[  100] loss: 0.014
[  200] loss: 0.010
[  300] loss: 0.019
[  400] loss: 0.019
[  500] loss: 0.015
[  600] loss: 0.014
Avg loss: 0.028398, accuracy:0.612441

Epoch 24
-------------------------------
[    0] loss: 0.019
[  100] loss: 0.013
[  200] loss: 0.013
[  300] loss: 0.010
[  400] loss: 0.026
[  500] loss: 0.014
[  600] loss: 0.013
Avg loss: 0.027605, accuracy:0.615943

Epoch 25
-------------------------------
[    0] loss: 0.009
[  100] loss: 0.016
[  200] loss: 0.007
[  300] loss: 0.022
[  400] loss: 0.020
[  500] loss: 0.016
[  600] loss: 0.027
Avg loss: 0.028171, accuracy:0.614616

Epoch 26
-------------------------------
[    0] loss: 0.019
[  100] loss: 0.004
[  200] loss: 0.017
[  300] loss: 0.020
[  400] loss: 0.007
[  500] loss: 0.007
[  600] loss: 0.015
Avg loss: 0.028214, accuracy:0.620283

Epoch 27
-------------------------------
[    0] loss: 0.017
[  100] loss: 0.008
[  200] loss: 0.014
[  300] loss: 0.016
[  400] loss: 0.014
[  500] loss: 0.018
[  600] loss: 0.012
Avg loss: 0.027267, accuracy:0.623009

Epoch 28
-------------------------------
[    0] loss: 0.018
[  100] loss: 0.013
[  200] loss: 0.014
[  300] loss: 0.019
[  400] loss: 0.014
[  500] loss: 0.021
[  600] loss: 0.010
Avg loss: 0.026904, accuracy:0.625602

Epoch 29
-------------------------------
[    0] loss: 0.009
[  100] loss: 0.021
[  200] loss: 0.012
[  300] loss: 0.015
[  400] loss: 0.014
[  500] loss: 0.013
[  600] loss: 0.012
Avg loss: 0.027337, accuracy:0.627155

Epoch 30
-------------------------------
[    0] loss: 0.016
[  100] loss: 0.008
[  200] loss: 0.017
[  300] loss: 0.006
[  400] loss: 0.016
[  500] loss: 0.011
[  600] loss: 0.017
Avg loss: 0.027576, accuracy:0.623085

Done!

四、结果分析

import numpy as np
import matplotlib.pyplot as plt

x = [i for i in range(1,31)]

plt.plot(x, test_loss_list, label="Loss", alpha=0.8)

plt.xlabel("Epoch")
plt.ylabel("Loss")

plt.legend()    
plt.show()

五、个人总结

在本次实战中，通过对标签的数字化处理，我们深入了解了 One-hot 编码的概念和应用。这是一种将分类数据转换成二进制向量表示的方法。与此同时，我们还探讨了多维分类任务中的一些独特挑战，尤其是在计算准确率（accuracy）时的不同处理方式。以下是对相关概念的详细总结和补充：

One-hot 编码（One-hot Encoding）

One-hot 编码是一种常用的技术，将分类数据转换为二进制向量表示。这种方法特别适用于处理离散的类别型数据。具体来说，每个类别被转换为一个长度为 N 的向量，其中 N 是所有可能类别的数量。在这个向量中，只有一个元素是 1，表示当前类别的位置，其余元素都是 0。

例如，假设我们有以下三个类别：['猫', '狗', '兔']，使用 One-hot 编码将它们转换为向量表示：

'猫' -> [1, 0, 0]
'狗' -> [0, 1, 0]
'兔' -> [0, 0, 1]

这种编码方式有助于机器学习算法处理分类数据，因为它消除了类别之间的内在顺序或大小关系，使得所有类别在模型训练过程中被平等对待。

多维分类任务（Multi-dimensional Classification Tasks）

在多维分类任务中，每个输入样本可能对应多个分类标签。例如，某些自然语言处理和计算机视觉任务中，一个样本可能需要同时进行多个独立的分类。处理多维分类任务时，我们通常需要对每个分类任务分别计算预测结果，并结合所有任务的结果来评估模型性能。

计算准确率（Accuracy）

在多维分类任务中，计算准确率的方式有所不同。以下是处理多维分类任务时的一些关键步骤：

预测和真实标签的处理：
- 对于每个样本的每个分类任务，分别计算预测结果和真实标签。
- 使用 argmax 等方法获取每个分类任务的预测类别。
准确率计算：
- 逐个任务计算每个样本的正确预测数量。
- 累积所有分类任务的正确预测数量。
- 将累积的正确预测数量除以总的分类任务数量，得到整体准确率。

通过本次实战，掌握了 One-hot 编码的基本概念和实现方法，并且深入理解了多维分类任务中准确率计算的特殊处理方式