逻辑回归详解

一、广义线性模型

1.1 指数分布族

一维的指数分布族: f λ ( y ) = exp ⁡ { λ y − Ψ ( λ ) } ⋅ f 0 ( y ) (1) f_{\lambda}(y)=\exp\{\lambda y-\Psi(\lambda)\}\cdot f_0(y)\tag1 fλ​(y)=exp{λy−Ψ(λ)}⋅f0​(y)(1)

1.2 常见的指数分布：

• $N(\mu ,{\sigma }^2)$，化成指数分布的话，$\lambda =\frac{\mu }{{\sigma }^2},\Psi (\lambda )=\frac{\mu }{2{\sigma }^2}$
• $Poi(\mu )$，化成指数分布的话，$\lambda =\ln \mu ,\Psi (\lambda )=\mu$
• $Bi(n,\pi )$，化成指数分布的话，$\lambda =\ln \frac{\pi }{1-\pi },\Psi (\lambda )=n\ln (1+e^{\lambda })$

1.3 广义线性模型

广义线性模型就是解决响应变量是服从二项分布、泊松分布或理论上是任何指数分布族的线性拟合问题。

现有$N$个观测点 y = { y 1 , ⋯   , y N } \bm y=\{y_1,\cdots,y_N\} y={y1​,⋯,yN​}来自某一指数分布族，即$$y_i\sim f_{{\lambda }_i}(\cdot ),i=1,\cdots ,N\text{\hspace{1em}(2)}$$
此时需要估计$N$个参数${\lambda }_1,\cdots ,{\lambda }_N$（观测点独立，但不同分布，具体的${\lambda }_i$不同）

通过线性回归，将$N$个参数的问题，转化为对$p$个参数的估计，这就是广义线性模型的核心策略。如下：

设$$\mathbf{\lambda }=\mathbf{X}\mathbf{\alpha }\text{\hspace{1em}(3)}$$
其中，$\mathbf{X}$为$N\times p$的结构矩阵，$\mathbf{\alpha }$为$p$维未知参数。

即$$\left[\begin{array}{c}{\lambda }_1\\ {\lambda }_2\\ ⋮\\ {\lambda }_N\end{array}\right]={\left[\begin{array}{c}{\mathbf{x}}_1\\ {\mathbf{x}}_2\\ ⋮\\ {\mathbf{x}}_N\end{array}\right]}_{N\times p}{\left[\begin{array}{c}{\alpha }_1\\ {\alpha }_2\\ ⋮\\ {\alpha }_p\end{array}\right]}_{p\times 1}\text{\hspace{1em}(4)}$$
亦即${\lambda }_1={\mathbf{x}}_1^{\top }\mathbf{\alpha }$，${\lambda }_2={\mathbf{x}}_2^{\top }\mathbf{\alpha }$，$\cdots$，${\lambda }_N={\mathbf{x}}_N^{\top }\mathbf{\alpha }$。例如，${\lambda }_1=x_{11}{\alpha }_1+x_{12}{\alpha }_2+\cdots +x_{1p}{\alpha }_p$

$\mathbf{y}$的联合密度函数为$$f(\mathbf{y})=\prod _{i=1}^N{f}_{{\lambda }_i}(y_i)=\exp \left\{\sum _{i=1}^N({\lambda }_i{y}_i-\Psi ({\lambda }_i))\right\}\prod _{i=1}^N{f}_0(y_i)\text{\hspace{1em}(5)}$$
化成向量形式为$$f(\mathbf{y})=\exp \left\{{\mathbf{\lambda }}^{\top }\mathbf{y}-\Psi (\mathbf{\lambda })\right\}{f}_0(\mathbf{y})\text{\hspace{1em}(6)}$$
此时有$N$个参数${\lambda }_1,\cdots ,{\lambda }_N$，再将$\mathbf{\lambda }=\mathbf{X}\mathbf{\alpha }$带入可得$$f_{\mathbf{\alpha }}(\mathbf{y})=\exp \left\{{\mathbf{\alpha }}^{\top }{\mathbf{X}}^{\top }\mathbf{y}-\Psi (\mathbf{X}\mathbf{\alpha })\right\}{f}_0(\mathbf{y})\text{\hspace{1em}(7)}$$
此时有$p$个参数${\alpha }_1,\cdots ,{\alpha }_p$

为进一步求解，令$\mathbf{z}={\mathbf{X}}^{\top }\mathbf{y}$，带入可得$$f_{\mathbf{\alpha }}(\mathbf{y})=\exp \left\{{\mathbf{\alpha }}^{\top }\mathbf{z}-\gamma (\mathbf{\alpha })\right\}\cdot f_0(\mathbf{y})\text{\hspace{1em}(8)}$$
其中，$\gamma (\mathbf{\alpha })=\Psi (\mathbf{X}\mathbf{\alpha })$

$(8)$式是$p$维参数的指数分布族，$\mathbf{z}$为充分统计量，故对一个$p$维的广义线性模型，其估计都依赖与$\mathbf{z}$，这样，不管$N$多大，只分析$p$维即可，避免了高维估计。

1.4 估计参数

用极大似然来估计参数$\mathbf{\alpha }$。

由$(8)$式可得:$$l_{\mathbf{y}}(\mathbf{\alpha })={\mathbf{\alpha }}^{\top }\mathbf{z}-\gamma (\mathbf{\alpha })+\ln f_0(\mathbf{y})\text{\hspace{1em}(9)}$$
求导得$$\frac{\partial }{\partial \mathbf{\alpha }}{l}_{\mathbf{y}}(\mathbf{\alpha })=\mathbf{z}-\frac{\partial }{\partial \mathbf{\alpha }}\gamma (\mathbf{\alpha })\text{\hspace{1em}(10)}$$
由于$\mathbf{z}={\mathbf{X}}^{\top }\mathbf{y}$，$\frac{\partial }{\partial \mathbf{\alpha }}\gamma (\mathbf{\alpha })=E_{\mathbf{\alpha }}(\mathbf{z})$，所以有$${\mathbf{X}}^{\top }\mathbf{y}-E({\mathbf{X}}^{\top }\mathbf{y})={\mathbf{X}}^{\top }\left(\mathbf{y}-E(\mathbf{y})\right)={\mathbf{X}}^{\top }\left(\mathbf{y}-\mu (\hat{\mathbf{\alpha }})\right)=0\text{\hspace{1em}(11)}$$
即未知参数$\mathbf{\alpha }$的极大似然估计满足$${\mathbf{X}}^{\top }\left(\mathbf{y}-\mu (\hat{\mathbf{\alpha }})\right)=0\text{\hspace{1em}(12)}$$

二、逻辑回归模型

2.1 基本思想

假设我们有$n$组分类数据， { y 1 , ⋯   , y n } \left\{y_1,\cdots,y_n\right\} {y1​,⋯,yn​}， y i ∈ { 0 , 1 } y_i\in\{0, 1\} yi​∈{0,1}，因变量服从伯努利分布，即$y_i\sim Bi(p_i)$， p i = P { y i = 1 ∣ x i } p_i=P\{y_i=1|\bm x_i\} pi​=P{yi​=1∣xi​}，逻辑回归本质上是估计$p_i$。

由于伯努利分布是指数分布族，所以可以用广义线性模型来估计$p_i$，所以逻辑回归是广义线性模型的一种。

2.2 模型的形式

由$1.3$节可知，对于$$y_i\sim f_{{\lambda }_i}(\cdot ),i=1,\cdots ,N\text{\hspace{1em}(13)}$$
需要先对参数$\mathbf{\lambda }$进行变换$$\mathbf{\lambda }=\mathbf{X}\mathbf{\alpha }\text{\hspace{1em}(14)}$$
即${\lambda }_i={\mathbf{x}}_i^{\top }\mathbf{\alpha }=x_{i,1}{\alpha }_1+\cdots +x_{i,p}{\alpha }_p$

对于伯努利分布$Bi(p)$，$\lambda =\ln \frac{p}{1-p}$，所以有$$\ln \frac{p_i}{1-p_i}={\mathbf{x}}_i^{\top }\mathbf{\alpha }=x_{i,1}{\alpha }_1+\cdots +x_{i,p}{\alpha }_p\text{\hspace{1em}(15)}$$

对上式化简可得$$p_i=\frac{\exp ({\mathbf{x}}_i^{\top }\mathbf{\alpha })}{1+\exp ({\mathbf{x}}_i^{\top }\mathbf{\alpha })}=\frac{1}{1+\exp (-{\mathbf{x}}_i^{\top }\mathbf{\alpha })}\text{\hspace{1em}(16)}$$

如果令$z_i=x_i^{\top }\mathbf{\alpha }$的话，上式可化为$$p_i=\frac{1}{1+\exp (-z_i)}\text{\hspace{1em}(17)}$$

这就是典型的$Sigmoid$函数$$g(z)=\frac{1}{1+\exp (-z)}\text{\hspace{1em}(18)}$$

这样，就将估计$n$个参数$p_1,\cdots ,p_n$转化为估计$p$个参数${\alpha }_1,\cdots ,{\alpha }_p$了，具体$p$的大小，根据我们选择有多少特征。

由$(15)$可知，$x_{i,1}{\alpha }_1+\cdots +x_{i,p}{\alpha }_p$并不是$y_i=1$的概率，而是对数几率（事件的几率$\frac{p}{1-p}$）

2.3 参数的估计

还是用极大似然法估计${\alpha }_1,\cdots ,{\alpha }_p$

$1.4$的推导的针对一般的广义线性模型，对于逻辑回归，我们可有：

似然函数为$$L=\prod _{i=1}^n{p}_i^{y_i}(1-p_i{)}^{1-y_i}\text{\hspace{1em}(19)}$$
对数似然函数为$$l=\sum _{i=1}^n\left[y_i\ln p_i+(1-y_i)\ln (1-p_i)\right]\text{\hspace{1em}(20)}$$
进行化简：$l=\sum _{i=1}^n\left[y_i\ln \frac{p_i}{1-p_i}+\ln (1-p_i)\right]=\sum _{i=1}^n\left[y_i({\mathbf{x}}_i^{\top }\mathbf{\alpha })-\ln (1+\exp ({\mathbf{x}}_i^{\top }\mathbf{\alpha }))\right]$

故对$$l=\sum _{i=1}^n\left[y_i({\mathbf{x}}_i^{\top }\mathbf{\alpha })-\ln (1+\exp ({\mathbf{x}}_i^{\top }\mathbf{\alpha }))\right]\text{\hspace{1em}(21)}$$
求极大值，即可得到参数$\mathbf{\alpha }$的估计

2.4 参数的求解

可用梯度下降法、牛顿法、拟牛顿法等进行求解

2.4.1 梯度下降法

梯度下降法是求解无约束最优化问题的一种最常用的方法，优点是实现简单。梯度下降法是一种迭代算法。先选取适当的初值$x^{(0)}$，不断迭代，更新$x$的值，进行目标函数的极小化，直到收敛。由于负梯度方向是使函数值下降最快的方向，在迭代的每一步，以负梯度方向更新$x$的值，从而达到减小函数值的目的。

为什么负梯度方向是使函数值下降最快的方向?

设函数$f(x)$在$x_k$附近连续可微,且$g_k=\nabla f(x_k)\ne 0$, 由Taylor展开式$$f(x)=f(x_k)+(x-x_k{)}^T\nabla f(x_k)+o(||x-x_k||)$$
可知, 若记$x-x_k=\alpha d_k$, 则满足$d_k^T{g}_k<0$的方向$d_k$是下降方向. 当$\alpha$给定后, $d_k^T{g}_k$越小, 即$-d_k^T{g}_k$越大, 函数下降越快. 由$Cauchy-Schwartz$不等式$$|d_k^T{g}_k|\le |d_k||g_k|$$
故当且仅当$d_k=-g_k$时, $d_k^T{g}_k$最小, 从而称$-g_k$时最速下降方向.

对$(21)$变形得$$l=\sum _{i=1}^n\left[-y_i({\mathbf{x}}_i^{\top }\mathbf{\alpha })+\ln (1+\exp ({\mathbf{x}}_i^{\top }\mathbf{\alpha }))\right]\text{\hspace{1em}(22)}$$
所以我们得目标是$$\underset{\mathbf{\alpha }}{\min }l\text{\hspace{1em}(23)}$$

对$(22)$求导得$$\frac{\partial }{\partial \mathbf{\alpha }}l=\sum _{i=1}^n(\frac{1}{1+\exp (-{\mathbf{x}}_i^{\top }\mathbf{\alpha })}-y_i){\mathbf{x}}_i\text{\hspace{1em}(24)}$$

所以可以得到参数$\mathbf{\alpha }$的更新方式为$${\mathbf{\alpha }}^{t+1}={\mathbf{\alpha }}^t-\eta \sum _{i=1}^n(\frac{1}{1+\exp (-{\mathbf{x}}_i^{\top }{\mathbf{\alpha }}^t)}-y_i){\mathbf{x}}_i\text{\hspace{1em}(25)}$$

梯度下降法又分为梯度下降法、随机梯度下降法和批次随机梯度下降法。

• 梯度下降法：每次更新参数用所有的样本。
  优点：得到的是全局最优解
  缺点：计算量打，速度慢
• 随机梯度下降法：每次更新参数用随机抽取的一个样本
  优点：速度快
  缺点：有可能陷入局部极小解
• 批次随机梯度下降法：每次更新参数用随机抽取的一部分样本，优缺点介于上述两种之间

2.4.2 牛顿法和拟牛顿法

牛顿法和拟牛顿法也是求解无约束最优化问题的常用方法，有收敛速度快的优点。牛顿法是迭代算法，每一步需要求解目标函数的黑塞矩阵的逆，计算比较复杂。拟牛顿法通过正定矩阵近似黑塞矩阵的逆矩阵或黑塞矩阵，简化了这一计算过程。

• 牛顿法：
  $${\mathbf{\alpha }}^{(t+1)}={\mathbf{\alpha }}^{(t)}-H_t^{-1}{g}_t\text{\hspace{1em}(26)}$$
  其中，$H(\mathbf{\alpha })={\left[\frac{{\partial }^{2}f}{\partial {\alpha }_i\partial {\alpha }_j}\right]}_{n\times n}$为黑塞矩阵，$g_t=\nabla f({\mathbf{\alpha }}^{(t)})$为$f(\mathbf{\alpha })$在${\mathbf{\alpha }}^{(t)}$处的一阶导的值。
• 拟牛顿法：
  用正定矩阵近似黑塞矩阵的逆矩阵或黑塞矩阵。

2.4.3 梯度下降法和牛顿法的对比

链接：最优化问题中，牛顿法为什么比梯度下降法求解需要的迭代次数更少？

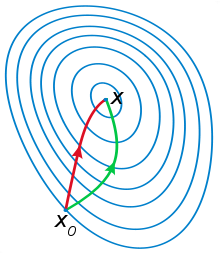
牛顿法比梯度下降法收敛的要快，这是因为牛顿法是二阶收敛，梯度下降是一阶收敛。事实上，梯度下降法每次只从当前位置选一个上升速度最大的方向走一步，牛顿法在选择方向时，不仅会考虑上升速度是否够大，还会考虑你走了一步之后，上升速度是否会变得更大，所以所需要的迭代次数更少。

下面是wiki上的图片，红色的牛顿法的迭代路径，绿色的是梯度下降法的迭代路径。

2.5 面试常见题

2.5.1 简单介绍一下算法

逻辑回归是在数据服从伯努利分布的假设下，通过极大似然的方法，运用梯度下降法来求解参数，从而达到将数据二分类的目的。

2.5.2 逻辑回归是如何做分类的

逻辑回归作为一个回归函数，如何用于分类问题。 逻辑回归中，对于每个$\mathbf{x}$，其条件概率$y$的确是一个连续的变量。而逻辑回归中可以设定一个阈值，$y$值大于这个阈值的是一类，$y$值小于这个阈值的是另外一类。至于阈值的选择，通常是根据实际情况来确定，一般情况下选取 0.5 作为阈值来划分。

2.5.3 逻辑回归损失函数

逻辑回归的损失函数是其极大似然函数。

2.5.4 逻辑回归中为什么使用对数损失而不用平方损失

对于逻辑回归，这里所说的对数损失和极大似然是相同的。 不使用平方损失的原因是，在使用 Sigmoid 函数作为正样本的概率时，同时将平方损失作为损失函数，这时所构造出来的损失函数是非凸的，不容易求解，容易得到其局部最优解。 而如果使用极大似然，其目标函数就是对数似然函数，该损失函数是关于未知参数的高阶连续可导的凸函数，便于求其全局最优解。

2.5.5 优缺点

• 优点：

  • 形式简单，模型的可解释性非常好。从特征的权重可以看到不同的特征对最后结果的影响，某个特征的权重值比较高，那么这个特征最后对结果的影响会比较大。

  • 训练速度快。分类的时候，计算量仅仅只和特征的数目相关。并且逻辑回归的分布式优化 SGD 发展比较成熟。

  • 方便调整输出结果，通过调整阈值的方式。

• 缺点：

  • 准确率欠佳。因为形式非常的简单，而现实中的数据非常复杂，因此，很难达到很高的准确性。
  • 很难处理数据不平衡的问题。
  • 只能处理二分类问题。处理多分类的话，需要一对一或一对多。

2.5.6 和线性回归的联系与区别

• 区别：
  • 一个是分类，一个是回归
  • 线性回归假设因变量服从正态分布，逻辑回归假设因变量服从伯努利分布
  • 线性回归优化的目标函数是平方损失，而逻辑回归优化的是对数损失
  • 线性归回要求自变量与因变量呈线性关系，而逻辑回归没有要求
• 联系：
  • 两个都是线性模型，线性回归是普通线性模型，逻辑回归是广义线性模型
  • 目标函数都可以认为是极大似然函数

2.5.7 需要标准化吗？

不需要，但如果加入了正则化，就需要，和线性回归一样。
详见数据特征 标准化和归一化

2.5.8 LR一般需要连续特征离散化原因

• 离散特征的增加和减少都很容易，易于模型快速迭代
• 稀疏向量内积乘法速度快，计算结果方便存储，容易扩展
• 离散化的特征对异常数据有很强的鲁棒性(比如年龄为300异常值可归为年龄>30这一段)
• 逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性（假设原本只有一个参数控制连续特征，离散化后，便有M个参数控制），能够提升模型表达能力，加大拟合；
• 离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
• 特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；

2.5.9 怎么样连续特征离散化？

等宽法、等频法、根据经验
详情见连续数据离散化最通俗的理解与操作

2.5.10 逻辑回归在训练的过程当中，如果有很多的特征高度相关或者说有一个特征重复了很多遍，会造成怎样的影响

如果在损失函数最终收敛的情况下，其实就算有很多特征高度相关也不会影响分类器的效果。 但是对特征本身来说的话，假设只有一个特征，在不考虑采样的情况下，你现在将它重复 N 遍。训练以后完以后，数据还是这么多，但是这个特征本身重复了 N 遍，实质上将原来的特征分成了 N 份，每一个特征都是原来特征权重值的百分之一。

2.5.11 为什么还是会在训练的过程当中将高度相关的特征去掉

• 去掉高度相关的特征会让模型的可解释性更好
• 可以大大提高训练的速度