非均匀有理B-样条(Non-Uniform Rational B-Splines, NURBS)基础知识

B样条是无理的，组成无理B样条曲线或曲面。有理曲线或曲面可以精确地表示圆锥截面。非均匀有理B样条(Non-Uniform Rational B-Splines, NURBS)就是为了表达更精确的曲面引入的，其控制顶点包含权重。NURBS的基函数与B样条不同，但结点向量、张量积的性质和细分规则是不变的。

1 几何角度

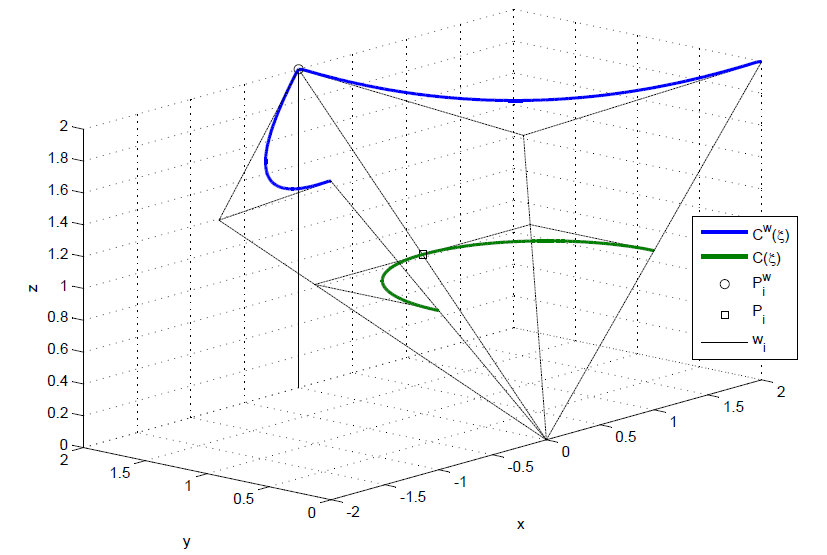
在${\mathbb{R}}^d$空间的NURBS实体通过在${\mathbb{R}}^{d+1}$空间的B样条实体投影得到，其中$d$是维数。图1说明了一个在${\mathbb{R}}^2$空间的半圆$C(\xi )$是如何通过在${\mathbb{R}}^3$空间的二次B样条曲线$C^w(\xi )$得到的。

控制顶点${\mathbf{P}}_i$的表示如下
$$({\mathbf{P}}_i{)}_j=\frac{({\mathbf{P}}_i^w{)}_j}{w_i}j=1,\dots ,d\text{\hspace{1em}(1)}$$
其中$w_i=({\mathbf{P}}_i^w{)}_{d+1}$而${\mathbf{P}}_i^w$是“投影控制顶点”。权重$w_i$在几何上是“投影控制顶点”的“高”，见图1。也就是说${\mathbb{R}}^d$维的NURBS实体中的控制顶点，是维的B样条控制顶点前几维分量除以最后一维分量得到的。

图1     B样条曲线投影到z=1平面，得到NURBS半圆

从几何上来讲，在NURBS中进行结点插入首先要将NURBS中的控制顶点投影到${\mathbb{R}}^{d+1}$维空间，之后使用B样条结点插入公式计算插入后的控制顶点，最后再将其投影到${\mathbb{R}}^d$维空间得到新的NURBS控制顶点。

2 代数角度

NURBS曲线的基函数表示为
$$R_i^p(\xi )=\frac{N_{i,p}(\xi )w_i}{W(\xi )}=\frac{N_{i,p}(}{{\sum }_{\hat{i}=1}^n{N}_{\hat{i},p}(\xi )w_i}$$