基于卡尔曼滤波算法的轨迹跟踪实例和python代码

卡尔曼滤波算法简介

卡尔曼滤波算法是比较经典的用于轨迹跟踪、轨迹平滑、状态估计的算法。

前提假设

卡尔曼滤波使用的前提之一是该系统是线性的，且维度有限。个人对线性系统的理解为下一时刻系统状态和当前时刻系统状态可以用一个线性关系函数来表达。这个线性关系只存在于前后时刻的系统状态间，长时间可以不成立。比如对于一个车辆轨迹的跟踪，每个时刻车辆的状态定义为[position, velocity]。前后时刻间的时长足够短的话，可以把车辆的运动近似为匀速运动。那么下一个时刻的车辆状态转移方程可以写成：position_next = position_pre + t * velocity_pre，velocity_next = velocity_pre，可以看出都为线性关系。因此可以称之为线性系统。
第二个前提是测量信息中包含的误差都为白噪音，即测量误差分布为高斯分布。一般来说检测器的随机误差都符合高斯分布。

特点

适用于连续变化的系统；
轻量化，只用保存上一状态的信息；
快速，适用于实时问题。

原理

详细的原理推荐大家学习此文章: https://www.bzarg.com/p/how-a-kalman-filter-works-in-pictures/

Python实例

本文构建了一个匀加速直线运动的物体，其中把加速度看成是控制变量。（其实也可以把加速度放入状态变量中进行考虑）模拟了20秒的跟踪，每秒更新一次。
其中有几个协方差矩阵比较绕，稍微解释一下：
1、Q表示外界噪音矩阵。可以理解为状态转移预测值和真实值之间的误差。有可能因为道路颠簸或其它外界原因导致的误差，是不太可知的。根据经验大概给一个靠谱的值就好。若设置Q<<R，则滤波会很信任估计值，若设置Q>>R则滤波器会很信任测量值。
2、R表示测量值和真实值之间的协方差矩阵。表示检测设备的误差，这理论上是可以检测出来的。
3、P表示状态协方差矩阵。表示估计值和真实值之间的误差大小。初始化为单位矩阵就好，会自动更新。
（备注：位置和速度可以看成两个独立变量，因此协方差矩阵只在对角线上有值）

import numpy as np
import matplotlib.pyplot as plt


class KalmanFilter:
    def __init__(self, F, B, u, Q, H, R, P):
        """
        :param F: 状态转移矩阵，固定
        :param B: 控制矩阵，固定
        :param u: 控制向量，例如加速度
        :param Q: 外界噪音，协方差矩阵，固定
        :param H: 单位转化矩阵，固定
        :param R: 观测值的协方差矩阵，固定
        :param P: 状态协方差矩阵，更新变化
        """
        self.F = F
        self.B = B
        self.u = u
        self.Q = Q
        self.H = H
        self.R = R
        # K为卡尔曼增益，基于H、P、R计算，更新变化
        self.K = 0
        self.P = P

    def predict(self, x0):
        x1 = np.dot(self.F, x0) + self.B * self.u
        self.P = np.dot(np.dot(self.F, self.P), self.F.T) + self.Q
        return x1

    def update(self, x1, z):
        P_ = np.dot(np.dot(self.H, self.P), self.H.T)
        self.K = np.dot(P_, np.linalg.inv(P_ + self.R))
        x_ = x1 + np.dot(self.K, (z - np.dot(self.H, x1)))
        # 更新P
        self.P = P_ - np.dot(self.K, np.dot(self.H, P_))
        return x_

if __name__ == "__main__":
    """
    构建初始速度为v0的匀加速运动的一维物体
    加速度为a, 作为控制信息
    状态为位置p和速度v
    用卡尔曼滤波来进行跟踪
    """
    # 总时间
    T = 20
    # 速度和加速度初始化值
    v0 = 0
    a = 1
    # 物体状态真实值
    p = [v0 * t + 0.5 * a * t**2 for t in range(T)]  # 真实位置
    p = np.array(p)
    v = [v0 + a * t for t in range(T)]  # 真实速度
    v = np.array(v)
    # 构建观测值
    # # 模拟白噪音,精确到小数点后两位
    sd_p = 3  # 位置标准差设置为3
    sd_v = 1  # 速度标准差设置为1
    noise_p = np.round(np.random.normal(0, sd_p, T), 2)  # 位置噪音
    noise_v = np.round(np.random.normal(0, sd_v, T), 2)  # 速度噪音
    # # 带有噪音的观测值
    z = np.array([p + noise_p, v + noise_v])
    # 实例化滤波器
    t = 1  # 时间间隔
    n = 2  # 物体状态[p, v]的维度
    F = np.array([[1, t], [0, 1]])  # 状态转移矩阵, [p_1, v_1] = [[1, t], [0, 1]] * [p_0, v_0]
    B = np.array([[0.5 * t**2], [t]])  # 控制矩阵, 描述控制变量和物体状态之间的关系
    u = a  # 控制向量，此例子中为加速度
    P = np.eye(n)  # 状态协方差矩阵初始化
    Q = np.array([[1, 0], [0, 1]])  # 外界噪音协方差矩阵
    H = np.eye(n)  # 单位转化矩阵
    R = np.array([[sd_p**2, 0], [0, sd_v**2]])  # 观测值协方差矩阵
    kf = KalmanFilter(F, B, u, Q, H, R, P)
    
    # 绘制真实值、观测值、滤波输出值三者之间的动态关系
    fusion = np.zeros([2, T-1])
    # 初始化
    x = z[:, 0].reshape((2, 1))
    # 绘图的x、y轴
    ax = []
    ay_real = []
    ay_sensor = []
    ay_fusion = []
    # 将 figure 设置为交互模式，figure 不用 plt.show() 也可以显示
    plt.ion()
    for i in range(T-1):
        x = kf.predict(x)
        x = kf.update(x, z[:, i+1].reshape((2, 1))) 
        fusion[0, i] = x[0, 0]
        fusion[1, i] = x[1, 0]
        ax.append(i+1)
        ay_real.append(p[i+1])
        ay_sensor.append(p[i+1]+noise_p[i+1])
        ay_fusion.append(x[0, 0])
        plt.clf()
        plt.plot(ax, ay_real, color='k', marker='o', markersize=5, label='real position')
        plt.plot(ax, ay_sensor, color='b', marker='^', markersize=5, label='sensory position')
        plt.plot(ax, ay_fusion, color='r', marker='s', markersize=5, label='fusion position')
        plt.legend()
        plt.pause(0.5)  # 暂停一段时间，不然画得太快会卡住显示不出来
        plt.ioff()  # 将 figure 设置为阻塞模式，也是 figure 的默认模式，figure 必须用 plt.show() 才能显示
    plt.show()
        

输出结果

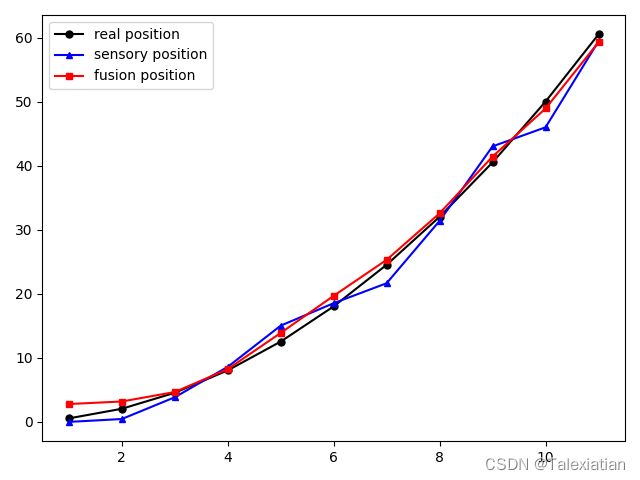
直观上来说卡尔曼滤波跟踪的轨迹比检测轨迹更接近真实轨迹。并且由于观测误差的存在，检测轨迹在真实轨迹周围波动明显，而滤波轨迹明显比检测轨迹更加平滑。

如有错误，欢迎指正！