LQR轨迹跟踪|python实现

LQR轨迹跟踪 | python实现

基本概念

离散LQR求解公式推导看这篇博客，这里直接给出结果。
$$\begin{array}{rl}& P_k=Q+A^T{P}_{k-1}A-A^{T}PB(B^T{P}_{k-1}B+R{)}^{-1}{B}^T{P}_{k-1}A\\ & K=(B^{T}PB+R{)}^{-1}{B}^{T}PA\\ & u^{\ast }(k)=-Kx(k)\end{array}$$
式中$P_k$表示LQR求解过程中的黎卡提矩阵迭代值，$P$表示收敛后的黎卡提矩阵；$K$表示反馈增益；$A,B$表示离散的系统矩阵；$Q,R$表示系统状态和输入的权重矩阵；$x,u$分别表示系统状态和系统输入，$u^{\ast }$表示最优系统输入。

求解步骤

1. 设置迭代最大值$N$和收敛差值$\epsilon$

2. 设置迭代初值$P_0=Q$

3. 迭代求解，$k=1,...,N$
   $$P_k=Q+A^T{P}_{k-1}A-A^{T}PB(B^T{P}_{k-1}B+R{)}^{-1}{B}^T{P}_{k-1}A$$
   若$|P_k-P_{k-1}|\le \epsilon$，表示黎卡提矩阵收敛，可以结束迭代，否则迭代至最大步数$N$。

4. 计算反馈增益
   $$K=(B^{T}PB+R{)}^{-1}{B}^{T}PA$$

5. 用反馈增益$K$进行控制
   $$u^{\ast }(t)=-Kx(t)$$

python实现轨迹跟踪

实现效果

图1 LQR轨迹跟踪效果示意

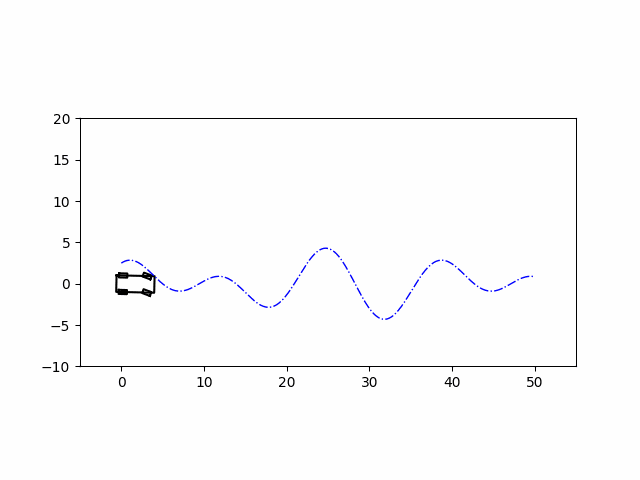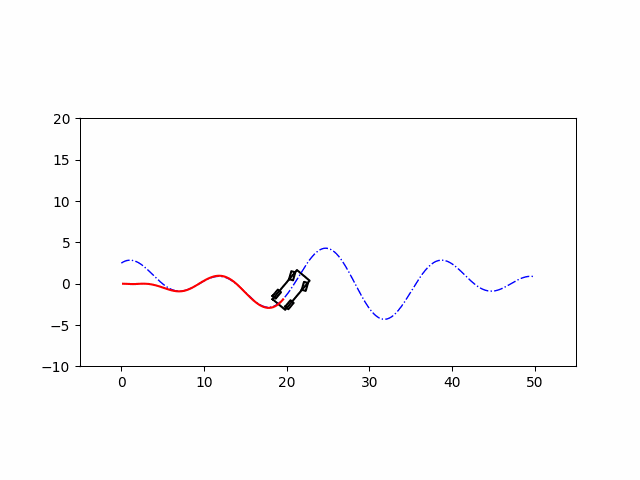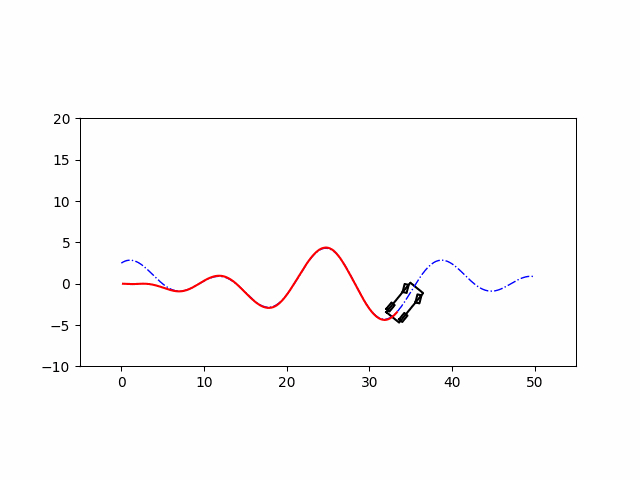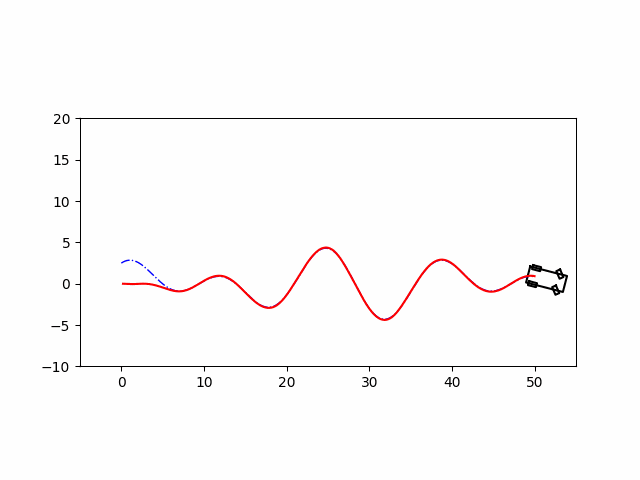
这里用LQR控制以后轴中心为车辆中心的模型进行轨迹跟踪，用这个模型是因为方便线性化进行控制，该模型线性化推导过程可以看这篇博客。

LQR求解

轨迹跟踪的完整代码在github仓库，这里给出LQR求解部分

import math
import numpy as np

class DiscreteLQR:
    def __init__(self, Ad, Bd, Q, R, epsilon = 1e-4):
        self.Ad = Ad # 离散系统矩阵
        self.Bd = Bd # 离散系统矩阵
        self.Q = Q
        self.R = R
        self.P = Q # 给个初始值Q
        self.K = np.mat(np.zeros([Bd.shape[1], Bd.shape[0]]))
        self.epsilon = epsilon
    
    # 离散LQR迭代求解，给定一个P的初值，迭代更新P和K，直到收敛
    def solve(self, MAX_ITER = 100):
        self.P = self.Q
        for it in range(MAX_ITER):
            P_ = self.Q + self.Ad.T * self.P * self.Ad - self.Ad.T * self.P * self.Bd * (self.R + self.Bd.T * self.P * self.Bd).I * self.Bd.T * self.P * self.Ad
            if (abs(P_ - self.P).max() < self.epsilon):
                break
            self.P = P_
        if (it == MAX_ITER - 1):
            print("Maximum iteration reached.")
            return False
        self.K = (self.R + self.Bd.T * self.P * self.Bd).I * self.Bd.T * self.P * self.Ad
        return True

    def update_mat(self, Ad, Bd, Q, R):
        self.Ad = Ad
        self.Bd = Bd
        self.Q = Q
        self.R = R