Iterated Tverberg Point-Theory

Abstract

这个算法是在写实验的时候要执行的，因为阅读的文档和最后的报告都是要用英文写，所以这里就用英文来写了，用的英文句子都比较简单，希望理解起来容易一些。所参照的论文，课件都在博文中说道。大家觉得算法介绍，执行不对的地方欢迎指出来共同探讨。

Iterated Tverberg point algorithm was used to compute an approximate of center point in computational geometry. Here, we use it to combine a set of models computed by machine learning algorithm to a much better model.

Definitions

1. Closed Halfspace is a set $\{x \in R^d: a \cdot x \leq b, a \in R^d, b\in R\}$.
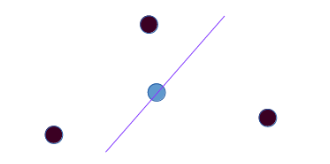
2. The Tukey depth of a point x with respect to a set P is the minimum number of points of P in any halfspace containing x. In the following figure, the depth of the blue point w.r.t the black points set is 1.
   
3. A point x is a centerpoint with respect to a set $P \subset R^d$ if depth of x is at least $\frac{n}{d+1}$.
4. Convex hull of a set A, denoted by conv(A), is the set of all convex combination of points in A. $conv(A) = \{x | \exists a_{1},...,a_{N} \in A, \alpha_{1},...,\alpha_{n} \geq 0; \sum_{i=1}^{N} \alpha_{i}=1; x=\sum_{i=1}^{N} \alpha_{i}a_{i}. \}$.

主要参照 http://www.cs.cmu.edu/afs/cs/academic/class/15456-s10/ClassNotes/

Theorems

这个部分的理论证明是后面算法执行必须要用的所以很必要。

1. Radon Theorem
   Let $a_1, a_2, ...,a_m \in R^d$, m $\geq d+2$, then there is a partition of {1,…,m} into I and J such that the convex hull of $\{a_i, i \in I\}$ and $\{a_j, j \in J\}$ is nonempty.

   Proof: Denote $b_i := (a_i, 1)$. There are $m \geq d+2$ vectors in $d+1$ dimensional space,
   thus they are linearly dependent. It means that there exists $\alpha_1,...,\alpha_m$ not all zero
   such that:
   

   $$\begin{equation} \sum_{i=1}^{m} \alpha_{i}b_{i}=0. \end{equation}$$
   Construct $I = \{i|\alpha_i \geq 0\}$ and $J=\{j| \alpha_j < 0\}$.
   As the last coordinate of $b_i$ is 1, thus:
   
   ∑i∈Iαi