数理方程的一些内容

临时备考用，有许多未完善地方，有错误欢迎纠正

三种方法

特征线法；分离变量法；积分变换法；
1.特征线法：就是列特征方程，令ξη带入…
2.分离变量法：就是令u(x,t)=X(x)T(t)，带入分成两组方程求解…
3.积分变换法：拉氏变换与傅氏变换（我们考拉氏变换）
阶:偏微分方程中最高阶偏导数的阶数称为偏微分方程的阶。
线性:偏微分方程中关于未知函数及其各阶偏导数都是一次的,且方程中的系数仅依赖于自变量,称为线性偏微分方程,否则称为非线性偏微分方程。
拟线性:在非线性偏微分方程中,如果关于未知函数的最高阶导数是一次的,则称之为拟线性偏微分方程。
半线性:在拟线性偏微分方程中,当未知函数的最高阶导数的系数不含未知函数及其低阶偏导数而仅依赖于自变量时,则称之为半线性偏微分方程。
自由项:在偏微分方程中,不含未知函数及其偏导数的项称为方程的自由项.。
齐次:若偏微分方程中的自由项为零,则称该方程为齐次方程,否则称为非齐次方程。
例子：

二阶非线性（拟线性）非齐次
一阶非线性（拟线性）齐次
二阶线性非齐次
三阶非线性（半线性）齐次
二阶非线性（半线性）非齐次

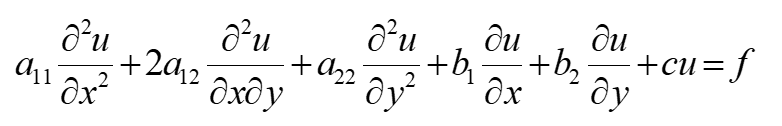
这里的a₁₁,a₁₂,a₂₂,b₁,b₂,c,f都是x和y的函数
记

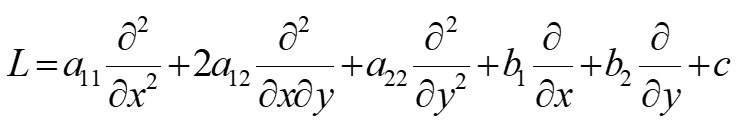
L称为线性微分算子。
一般而言,一个m阶偏微分方程,其未知函数是n元函数,那么通解中含有m个n-1元的任意函数。

叠加定理

叠加原理对任意阶的线性齐次偏微分方程都适用,而对非线性偏微分方程是不成立的
1.若u₁,u₂…u_n都满足线性齐次方程 L[u]=0，则它们的线性组合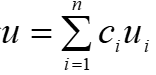
必满足方程L[u]=0,其中u₁,u₂…u_n为不同时为零的常数。
2.若u₁,u₂…u_n满足L[u]=0,而

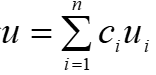
在求解区域上一致收敛,且可逐项求出方程中所出现的各阶偏导数,则

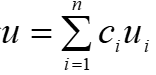
也满足方程 L[u]=0 。

三类经典方程

1.波动方程(也称为双曲型方程)
2.热传导方程(也称为抛物型方程)
3.拉普拉斯方程(也称为椭圆型方程)

波动方程

一维：

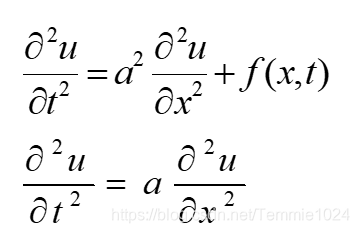
二维：

三维：

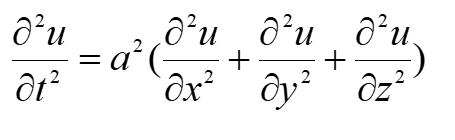
热传导方程

拉普拉斯方程和泊松方程

三维泊松方程

三维拉普拉斯方程

三维拉普拉斯算子

定解条件

定解条件: 包括初始条件和边界条件

初始条件

描述系统或过程的初始状态的条件
波动方程的初始条件

热传导方程的初始条件

拉普拉斯方程和泊松方程描述的是系统的稳定状态,和时间t无关,因而不需要初始条件
初始条件的个数与方程中未知函数关于时间偏导数的阶数相同

边界条件

描述系统或过程的边界状态的条件,常见的边界条件有三类

也可以统一写作

二阶线性齐次微分方程通解公式

写出特征方程

计算r₁与r₂的值

1. r₁≠r₂，且都为实数。通解为
   
2. r₁=r₂，且都为实数。通解为
   
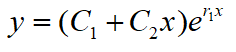
3. r₁与r₂为共轭复根（a±bi）。通解为
   

含两个自变量的二阶线性偏微分方程的分类和化简

判断方程类型

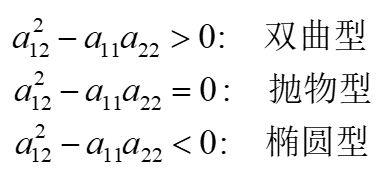
化简

方程为双曲线型

令ξ=φ(x,y) η=ψ(x,y)带入原式

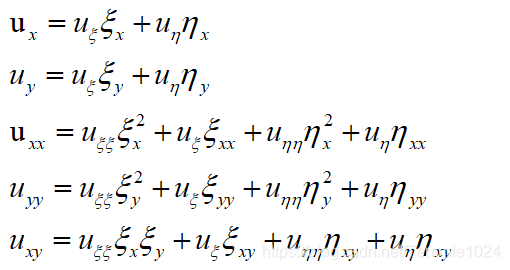
方程为抛物线型

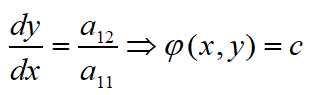
这时ψ(x,y)任意取单要满足一定条件，通常选择x或y即可。
再令ξ=φ(x,y) η=ψ(x,y)带入原式
方程为椭圆型

再令ξ=φ(x,y) η=ψ(x,y)带入原式

行波法（特征线法）

一维波动方程的初值问题

达朗贝尔公式

对于波动方程的初值问题

依旧可以根据上面的化简方法进行化简计算。达朗贝尔公式就是这样推导出来的。.


其结果为：

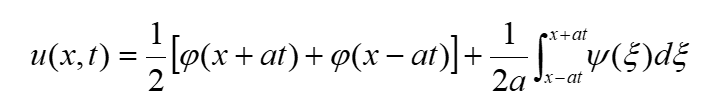
分离变量法

其次线性方程使用令u(x,t)=X(x)T(t),带入原方程化简。

非齐次问题

非齐次边界条件齐次化

设u(x,y)=v(x,t)+w(x)利用叠加性，使w(x,y)的边界条件非齐次，v(x,t)的边界条件齐次

解非齐次方程

方程非齐次与边界条件非齐次。
1.如果边界条件非齐次，那么令u(x,t)=v(x,t)+w(x,t)
根据给出的条件，经常设w(x,t)为：

2.如果边界条件齐次（或根据上面化成了齐次），方程非齐次，使用级数，设v(x,t)=∑T(t)sin(nπx/l),f(x,t)=∑f_n(x,t)sin(nπx/t)带入计算

拉氏变换

线性性质

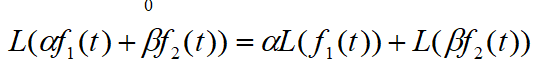
微分性质

若n-1阶导数在0点均为0，则

积分性质

位移性质

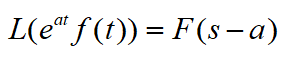
延迟性质