【文献阅读】Model Compression and Efficient Inference for Large Language Models: A Survey

摘要

基于 Transformer 的大型语言模型取得了巨大成功。然而，推理过程中高昂的内存和计算成本使得在资源受限的设备上部署大型模型颇具挑战。本文从算法角度研究了大型语言模型的压缩和高效推理方法。在分类方面，与较小的模型类似，大型语言模型的压缩和加速算法仍可分为量化、剪枝、知识蒸馏、紧凑架构设计和动态网络。不过，大型语言模型与较小模型相比有两个显著特点：（1）大多数压缩算法在压缩后需要对模型进行微调甚至重新训练。大型模型最显著的问题是模型微调或训练的成本极高。因此，许多针对大型模型的算法，如量化和剪枝，开始探索无调优算法。（2）大型模型强调通用性和泛化能力，而非在单个任务上的性能。所以，许多算法，如知识蒸馏，关注的是如何在压缩后保持其通用性和泛化能力。由于这两个特点在早期大型模型中并不十分明显，我们进一步将大型语言模型分为中型模型和 “真正的” 大型模型。此外，我们还介绍了一些成熟的大型模型高效推理框架，这些框架可以支持基本的压缩或加速算法，极大地方便了用户进行模型部署。

关键词：大型语言模型；模型压缩；高效推理；量化；剪枝；知识蒸馏；紧凑架构设计；动态网络

 1 引言

大型语言模型（LLMs）已成为人工智能领域中一个重要且热门的话题。与以往的语言模型相比，大型语言模型（如ChatGPT、LLaMA、Claude）对未见数据展现出更强的泛化能力。此外，它们甚至呈现出许多小模型所不具备的能力（即涌现能力），比如多步推理和遵循指令的能力。这些进展彰显了大型语言模型的巨大潜力。

然而，推理过程中高昂的内存和计算开销也阻碍了大型语言模型的部署。例如，一个权重为float32的100亿参数模型需要消耗37GB内存，更不用说推理内存成本会随着序列长度的平方而进一步增加。为了在资源受限的设备甚至移动设备上部署模型，许多大型语言模型借助量化等模型压缩方法来降低推理内存和计算成本。

深度学习模型的压缩领域出现的时间比大型语言模型要早得多。它假定我们已经有一个预定义（甚至是预训练）的模型。模型压缩旨在降低模型在推理过程中的内存和计算成本，使模型能够在各种资源受限的设备上运行。从算法角度来看，常见的模型压缩方法包括：
量化：将float32的权重或激活值转换为低比特的浮点数或整数。比特数越少，所需内存越少。此外，更少的比特数可能意味着更高的并行性和更快的推理速度。
剪枝：致力于去除预先设计好的模型中不重要的组件（如神经元、层等），从而降低推理过程中的内存和计算成本。
知识蒸馏：引入一个预训练的大型模型作为教师模型，并将其知识转移到一个新的较小模型（称为学生模型）中。然后，较小的模型将具备与教师模型近乎相同的能力，同时占用更少的内存和计算成本。
紧凑架构设计：设计成本更低的新算子来替代（通常是近似替代）原始模型中繁琐的算子。对于Transformer模型，自注意力机制是主要的优化目标，常常被其他算子所取代。
动态网络：对每个推理样本区别对待。原始模型是一个超网络，每个样本仅选择超网络的一个子结构进行推理。专家混合（MoE）就是一种动态推理方式。

此外，上述方法还可以结合使用，以实现进一步的压缩和加速。现有的压缩方法为我们压缩大型语言模型提供了重要的基础和思路。然而，大型语言模型也给模型压缩带来了许多新的挑战：
1. 许多先前的模型压缩方法在压缩后通常需要对模型进行微调。然而，由于大型语言模型的微调成本极高，研究人员不得不探索无微调或至少是更高效的微调方法。
2. 大型语言模型强调在各种任务和未见数据上的通用性和泛化能力，甚至是涌现能力，而不是像神经机器翻译那样处理单个任务。因此，压缩后的大型语言模型需要更仔细地验证其通用性和泛化能力。

为了应对这些挑战，人们提出了许多专门针对大型语言模型的压缩方法。在本文中，我们将对这些方法进行全面的综述。为了更好地介绍这些方法，我们进一步将参数在10亿左右或更少的语言模型（如BERT、GPT2）单独划分出来，称它们为中型模型，尽管它们通常也被视为大型语言模型。而参数超过10亿的模型（如LLaMA、Claude、ChatGPT等）则保留大型语言模型的名称。这是因为中型模型受上述两个挑战的影响较小，即中型模型相对更容易微调，展现出的涌现能力也较少。因此，许多针对中型模型的压缩方法仍然与针对较小模型的方法相似。

本文后续章节安排如下：第2节将介绍一些预备知识。然后，我们将在第3、4、5、6、7、8节分别讨论剪枝、知识蒸馏、量化、紧凑架构设计和动态网络。

 2 预备知识

在本节中，我们将介绍一些关于Transformer、大型语言模型、参数高效训练等方面的重要预备知识。

 2.1 Transformer

Transformer最早在[1]中被提出，最初用于机器翻译。其基本结构如图1所示。输入（一个句子）通常通过嵌入层投影为一系列向量（称为标记），作为Transformer的输入。每个Transformer块由一个注意力模块和一个多层感知器（MLP）模块组成。
注意力机制：对于输入序列中的每个标记，它首先通过线性函数映射为查询向量（Q）和/或键值对向量（K和V）。然后，注意力模块可以描述为将一个查询向量和一组键值对映射为一个输出。输出通过对值向量进行加权求和计算得到，其中分配给每个值向量的权重由查询向量与相应键向量的兼容性函数计算得出。最常见的注意力模块是缩放点积函数：
\(Attention(Q, K, V)=softmax\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V\) (1)
其中，权重通过Q和K的点积计算得出，\(\sqrt[n]{d_{k}}\)是一个常数缩放因子。
多头注意力机制：此外，Transformer不是使用单个注意力函数处理键、值和查询，而是采用多头注意力机制[1]，如图1所示。它通过不同的线性层将输入标记映射为h个不同的查询、键和值（\(({Q_{i}, K_{i}, V_{i} | i \in[1, h]})\) ）。然后，最终输出为：
\(\begin{aligned} Muti-Head Attention & =Concat\left( head _{1}, \cdots, head _{h}\right) W_{o} \\ head _{i} & =Attention\left(Q_{i}, K_{i}, V_{i}\right), \end{aligned}\)
其中\(Wo\)是一个线性投影矩阵。
编码器和解码器：最初的Transformer用于神经机器翻译，采用编码器 - 解码器结构。编码器首先独立处理输入序列（例如，用源语言书写的文本），解码器将编码器的输出作为输入，并预测最终输出（例如，目标语言）。编码器和解码器的注意力模块有两个核心区别：（1）编码器采用全注意力机制，输入序列中的任意两个标记都可以相互可见。另一方面，解码器采用单向注意力机制。这是因为解码器逐个生成输出标记，每个标记只能看到其之前的输出标记。（2）编码器采用自注意力模块，即Q、K、V都来自源语言的输入标记。相比之下，解码器采用交叉注意力机制，其中K、V来自编码器的输出，而Q是解码器的最后一个输出标记。随着发展，除了编码器 - 解码器模型（例如T5 [2]），许多后续的语言模型也采用纯编码器结构（例如BERT [3]）和纯解码器结构，如GPT系列[4,5,6]模型。

虽然我们简要介绍了Transformer中的一些重要概念，但更详细的介绍可参考许多先前的综述[7,8]。

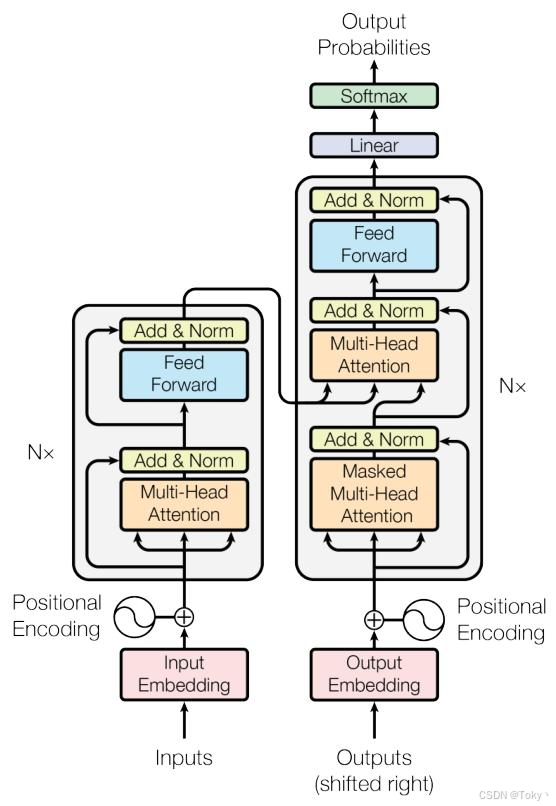
图1：源自[1]的Transformer架构

 2.2 中型/大型语言模型

随着Transformer的成功，越来越多基于纯Transformer的语言模型涌现，模型的参数数量也在不断增加。尽管对于大型语言模型的参数规模没有具体的阈值，但通常认为 “大型” 语言模型可以追溯到2018年提出的BERT [3]和GPT - 1 [4]，它们的参数规模都达到了数亿。

此后，更多的语言模型如GPT - 3 [9]、盘古 [10]、T5 [2]、CPM - 2 [11]、BLOOM [12]、OPT [13]、GLM [14]、PaLM [15]、QWen [16]、ERNIE [17]、LLaMA [18]等被提出。除了参数规模，这些模型与之前模型最显著的区别在于它们的涌现性。正如[19]中所提出的，大型语言模型利用大规模自监督预训练，使模型具备许多小模型中未出现的能力（即涌现能力），包括多步推理、遵循指令、程序执行能力等。例如，GPT - 3、LLaMA和许多其他大型语言模型可以通过上下文学习解决少样本任务，甚至是零样本任务。大型语言模型的突破展示了其在解决一系列复杂任务时相较于小模型令人惊讶的能力（称为涌现）。

为了进一步强调这种差异，我们将参数超过数亿的语言模型分为中型模型和大型模型。具体来说，参数在10亿左右或更少的模型称为中型模型，而参数超过10亿的模型称为大型模型。

 2.3 参数高效微调（PEFT）

正如我们在引言中所讨论的，许多模型压缩算法，如知识蒸馏和剪枝，在压缩后需要进行微调甚至重新训练以恢复精度。然而，对于中型或大型模型来说，全参数微调或训练的成本非常高。为此，人们提出了许多参数高效微调（PEFT）算法。它们致力于尽可能少地微调参数或训练轮次，以降低微调成本。在本文中，我们主要讨论推理阶段（而非训练/微调阶段）的模型压缩和加速算法，但我们仍在附录A中补充了一些PEFT算法。

 3 量化

量化是指将输入值从一个较大（通常是连续）的集合映射到一个较小（通常是有限）的集合的过程（例如，图2展示了一个示例）。这是降低大型语言模型内存成本和提高推理速度最直接的方法，尤其是在支持低比特数据类型快速运算的硬件（如INT4）上。需要注意的是，量化在神经网络训练[20]和推理中都取得了显著成功，而本综述仅关注推理部分。

量化方法相较于其他压缩方法（如剪枝和蒸馏）有几个优点：1）压缩比高：将大型语言模型中的权重从32位浮点数量化为4位整数可以大幅将模型大小压缩至约八分之一，这对于像大型语言模型推理这样受内存限制的过程至关重要；2）成本低：许多量化方法不需要重新训练整个大型语言模型，这使得计算资源有限的研究人员更容易负担；3）灵活性高：量化与大多数其他压缩方法兼容，这为进一步提高性能提供了绝佳机会。

为了帮助读者更好地理解量化方法，我们将在3.1小节首先介绍标准量化方法和一些基本概念。然后，在3.2节中，我们将简要总结在大型语言模型出现之前，针对中型语言模型（如BERT、GPT2等）的一些最重要的工作。3.3节和3.4节涵盖了专注于大型语言模型推理的量化方法的最新进展。考虑到重新训练一个拥有数十亿参数的模型的困难，我们通常根据技术是否需要重新训练，将大型语言模型量化方法分为两部分。3.3节讨论无需重新训练的方法（即训练后量化，PTQ），而3.4节讨论需要重新训练的方法（即量化感知训练，QAT）。最后，在3.5节中，我们讨论一些在前面章节未涵盖，但具有未来研究潜力的高级话题。

图2：(a) 均匀量化将一个实值范围划分为均匀、有限的区间，然后将同一区间内的实值映射到相同的整数。(b) 一个FP16张量被量化为INT4格式，然后再反量化回FP16。

 3.1 基本概念

量化的历史比神经网络长得多，具体的量化方法也多种多样。为了让读者清晰地理解各种量化概念，我们将首先介绍标准均匀量化和相应的反量化过程。之后，我们解释在不同量化方法中经常提到的几个基本概念。

1. 均匀量化：量化最基本的形式是将一个实值范围划分为均匀、有限的区间（例如，对于b位整数，划分为\(2^{b}\)个区间），然后将同一区间内的实值映射到相同的整数。这个过程的公式如下：
\(Q(r)=ROUND\left(\frac{r}{S}\right)+Z\)
其中\(Q(\cdot)\)是量化算子，r是要量化的实值，S是一个实值缩放因子，Z是一个整数零点，ROUND(·)是一个舍入操作（例如，四舍五入到最接近的整数）。这种方法被称为均匀量化，因为每个区间的长度相同（等于缩放因子S），并且量化值是均匀分布的（例如，整数0、1、2，...）。

从量化值恢复实值的操作称为反量化：
\(\overline{r}=S \cdot(Q(r)-Z)\)
需要注意的是，由于ROUND(·)函数引入的信息损失，恢复的值\(\bar{r}\)可能与原始实值r不同。

2. 非均匀量化：与均匀量化相对的是非均匀量化，在非均匀量化中，量化值不一定是均匀分布的，区间的长度也可以不同。非均匀量化的一般公式为：
\(Q(r)=Q_{i}, if r \in\left[\Delta_{i}, \Delta_{i+1}\right)\)
其中\(Q_{i}\)是候选量化值，称为量化级别，\(\Delta_{i}\)和\(\Delta_{i+1}\)定义了一个区间，实值将被映射到相应的\(Q_{i}\)。

在固定比特宽度的情况下，非均匀量化通常比均匀量化能实现更高的精度和更低的量化误差，因为神经网络的权重通常不是均匀分布的。然而，非均匀量化方法可能计算效率较低，因为这些方法通常涉及耗时的查找操作，无法直接与GPU等并行计算硬件兼容。

3. 裁剪范围和校准：与均匀量化相关的一个重要因素是裁剪范围\([\alpha, \beta]\)，使得低于α或高于β的实值将分别被裁剪为α或β。裁剪范围也直接影响均匀量化中的缩放因子S：
\(S=\frac{\beta-\alpha}{2^{b}-1}\) (6)
选择裁剪范围的过程称为校准。常见的校准选择包括使用最小/最大值（即\(-\alpha=r_{min }\) ，\(\beta=r_{max }\) ）、使用绝对最大值（即\(-\alpha=\beta=max (|r|)\) ）或最小化实值和量化值之间的信息损失（即KL散度）。

4. 对称/非对称量化：当裁剪范围\([\alpha, \beta]\)关于0对称（\(\alpha+\beta=0\)且\(Z = 0\)）时，相应的方法通常称为对称量化；否则为非对称量化。

非对称量化的裁剪范围更紧凑，这对于神经网络中的激活值尤为重要，因为其范围可能显著不平衡（例如，在ReLU激活函数之后，所有激活值都变为非负）。然而，对称量化在反量化步骤中计算效率更高。

5. 量化粒度：神经网络量化的一个分类标准是粒度，它对应于哪些权重/激活值一起被量化并共享量化参数。我们从粗到细列出典型的粒度如下：

•     层粒度：卷积层中所有滤波器的权重或线性层的全权重矩阵一起被量化。
•     通道粒度：卷积层中单个滤波器的权重一起被量化。
•     行/列粒度：线性层权重矩阵的单个行/列的权重一起被量化。
•     标记粒度：每个标记的激活值一起被量化。
•     组粒度：权重或激活值中的几个连续实值被视为一组并一起被量化。组大小通常较小（例如，64个连续实值）。

一般来说，更细的粒度将模型权重或激活值划分为更小的组，可以减少量化误差。然而，更细的粒度需要存储更多的量化参数，并在计算过程中引入更高的量化开销。

需要注意的是，不同的工作可能使用不同的符号。为了清晰起见，在本综述中，我们设输入\(X \in \mathbb{R}^{N ×D_{in }}\) ，权重矩阵\(W \in \mathbb{R}^{D_{in } ×D_{out }}\) ，其中N是批量大小，\(D_{in }\)和\(D_{out }\)分别是输入和输出维度。一个线性层可以写为\(Y=X W \in \mathbb{R}^{N ×D_{out }}\) 。

6. 训练后量化/量化感知训练：减少量化误差的一种有效方法是通过训练。量化方法可以分为量化后是否需要重新训练：
    训练后量化（PTQ）：无需重新训练的方法，量化后的模型可直接用于推理。
    量化感知训练（QAT）：需要重新训练的方法，有助于恢复量化引入的误差。

量化对训练好的模型参数造成的扰动可能会使模型偏离其在浮点精度训练中收敛的点。QAT通过在重新训练中模拟量化过程（例如，在计算图中注入模拟权重量化的节点）或使用额外参数微调量化后的模型（例如，与Adapters或LoRA结合）来解决这个问题，使模型能够学习收敛到一个在量化后性能更好的点。然而，对拥有数十亿参数的完整大型语言模型进行重新训练，对大多数研究人员来说成本难以承受。因此，PTQ方法也被广泛研究，以通过特定的非训练方法（例如最优脑外科手术算法）在不引入额外计算预算的情况下实现更好的性能。

一般来说，量化中的舍入操作是一个不可微的过程，所以QAT乍一看似乎是不可能的。然而，研究人员发现一种称为直通估计器（STE）的简单方法在大多数情况下效果良好，该方法忽略舍入操作，并用恒等函数对其进行近似。

7. 静态/动态量化：神经网络权重和激活值量化的一个关键区别在于，权重在推理过程中大多是固定的，因此可以静态计算裁剪范围校准中使用的统计信息。而激活值并非如此，因为其范围和统计信息直到运行时才知道。因此，激活值量化可以分为两类。
    静态量化：指的是在推理前使用一些校准输入来预计算量化参数以找到典型的激活统计信息，或者在神经网络训练期间联合学习这些参数的方法。
    动态量化：在运行时动态计算量化参数，通常比静态量化更准确，但计算所需统计信息（如最小值、最大值等）的开销可能较高。
8. 模拟/仅整数量化：还有一种分类标准是量化值是否用于实际运算（例如矩阵乘法）。对于模拟量化（也称为伪量化），权重和激活值仅以低比特数据类型（如INT4）存储，在进行实际运算时必须反量化为高比特数据类型（如float16）。对于仅整数量化，运算可以使用低比特数据类型进行。模拟量化可以减少神经网络的内存成本和数据移动时间，这很有帮助，因为一些研究表明大型语言模型推理受内存限制而非计算限制。相比之下，仅整数量化可以进一步利用特定硬件支持的高效低比特运算来加速。
9. 仅权重量化/权重+激活值量化：量化目标是仅权重还是权重和激活值两者。先前的工作[21]发现激活值量化通常比权重量化更敏感，所以仅权重量化可以达到更低的比特宽度。然而，权重量化后在与激活值相乘之前必须进行反量化，所以仅权重量化不能是仅整数的，并且会在推理过程中引入额外的计算开销。

我们简要介绍了量化中一些最重要的概念。这些概念普遍适用于所有神经网络量化，并且每种具体方法可能适用于几种不同的概念（例如，一种用于大型语言模型的均匀对称动态层粒度模拟量化方法）。我们根据这些基本概念在表1中对大型语言模型的主要量化方法进行了分类。
表1：几种强大的大型语言模型量化基线方法的详细分类。✓表示一种量化方法属于特定类别，×表示不属于，◦表示一种量化方法在两种情况下都可以使用。对于在不同比特宽度下工作的方法，我们报告最低有效比特宽度。有关每个类别的详细解释，请参见3.1小节。

 3.2 中型语言模型的量化方法

为了便于表达，我们将规模小于或接近10亿参数的模型称为中型语言模型，以BERT、GPT - 2和BART为代表。

中型语言模型的量化方法[22]主要采用QAT框架而非PTQ，因为重新训练这样一个模型的成本相对可以接受。重新训练带来的评估指标（如准确率）的提升非常显著，尤其是在极低比特设置（如1比特或2比特量化）下。因此，我们将首先介绍中型语言模型的主流方法，即QAT方法，然后介绍PTQ方法。

 3.2.1 中型语言模型的QAT

早期的工作旨在将类似BERT模型的权重量化为INT8。Q8BERT [23]应用了来自[24]的基本QAT框架，将BERT的权重和激活值都量化为8比特，且模型性能没有显著下降。

一些工作使用更复杂的方法实现了低于8比特的量化[25,26,27,28,29,30,31]。例如，Q - BERT [25]保持8比特的激活值，同时将混合精度的权重降低到2/3比特。它使用海森矩阵来确定每层权重的比特宽度，以便对相应海森矩阵顶部特征值较小的层进行更激进的量化。此外，TernaryBERT [27]将其权重限制为 - 1、0、+ 1，仅使用2比特，并采用8比特的激活值。它通过最小化原始模型和量化模型之间激活值和注意力分数的均方误差（MSE）来采用知识蒸馏，以克服性能下降的问题。在TernaryBERT之后，BinaryBERT [32]将BERT量化的极限推进到权重量化，即将权重限制在\({-\alpha,+\alpha}\) 。作者提出通过从半尺寸的TernaryBERT等效拆分来初始化BinaryBERT，以继承三元模型的良好性能。此外，BiBERT [28]是BERT的全量化（即1比特权重、嵌入和激活）。作者发现全二元模型的严重性能下降来自信息退化和优化方向不匹配。因此，提出了双注意力结构和方向匹配蒸馏（DMD）方案，以保留原始BERT的大部分能力。

一些工作实现了模型性能下降和量化比特宽度之间的自动平衡。Zhao等人[29]利用可微神经架构搜索方法自动为参数分配精度。具体来说，在一个结合了交叉熵损失和模型大小惩罚的目标函数下，交替优化权重和权重的比特分配。优化过程旨在为每组参数获得一组接近最优的比特分配。

 3.2.2 中型语言模型的PTQ

PTQ方法经过精心设计，通常不需要额外的微调或重新训练来补偿量化误差。GOBO [33]使用非均匀量化（即聚类）将绝大多数符合高斯分布的权重量化为3比特，并将少数异常值权重单独以FP32保存。I - BERT [34]为特定的非线性函数（如GeLU、Softmax、LayerNorm）设计了仅整数近似方法，以实现无需任何浮点计算的端到端仅整数BERT推理。Dai等人[35]使用更细的粒度来减少量化误差。具体来说，作者将权重和激活值量化为4比特，采用组粒度量化（例如，将16 - 64个连续权重视为一组）。使用校准集来确定每组的缩放因子。

此外，需要注意的是，通过精心定制的PTQ方法获得的量化参数，通常可以作为QAT方法中重新训练的良好初始化点。

 3.2.3 量化生成式中型语言模型

尽管上述针对类似BERT模型的量化方法取得了成功，但在生成式大型语言模型出现之前，对生成式语言模型（如GPT、BART）进行量化的尝试很少[36]。关键区别在于量化误差会在逐个标记的生成过程中累积，因此量化生成式语言模型通常是一个更复杂的问题。

根据Tao等人[37]的研究，直接将为类似BERT模型设计的量化方法应用于生成式语言模型会受到同质词嵌入和权重分布差异的阻碍。同质词嵌入是指生成式语言模型的词嵌入在量化后变得彼此难以区分的问题。另一方面，权重分布差异意味着模型的权重高度偏斜且存在异常值。为了解决这些挑战，作者提出了两种解决方案：标记级对比蒸馏和模块依赖动态缩放。

DQ - BART [38]使用QAT框架和蒸馏训练目标，联合蒸馏和量化序列到序列模型BART。DQ - BART采用标准对称均匀量化，如公式(3)所示，并将训练目标设置为最小化量化和蒸馏后的低精度学生模型与全精度教师模型之间的输出logits、注意力和隐藏状态的差异。

在本节中，我们仅简要介绍了在中型语言模型上完成的最重要的工作。有关中型语言模型量化方法的更详细总结，感兴趣的读者可参考[39,40]。

 3.3 大型语言模型的训练后量化

在过去几年中，大型语言模型的训练后量化（PTQ）方法显著增加。部分原因是PTQ不涉及大型语言模型极其昂贵的重新训练过程，所以对大多数研究人员来说这是一个更可行的方向。

此外，我们大致将大型语言模型的PTQ工作分为两类：仅权重量化和权重+激活值量化。我们将在以下部分分别讨论与这两类相关的工作。

 3.3.1 仅权重量化

在本部分中，我们关注仅对大型语言模型的权重（而非激活值）进行量化的问题。一般来说，仅权重量化属于模拟量化方法；权重仅以低比特数据类型存储，在实际计算前需要进行反量化。这意味着此类方法可以减小大型语言模型的整体大小，并减少在内存之间移动权重的时间，但无法享受特定硬件支持的加速低比特运算。

虽然前面的小节讨论了各种可用于量化中型语言模型的方法，但大型语言模型因其独特的特性带来了额外的挑战。这些挑战包括：
1. 大型语言模型在推理过程中严重依赖内存，尤其是当推理批量大小较小时[49]。这使得最小化内存使用和优化不同存储设备之间的数据传输至关重要。
2. 大型语言模型的激活模式独特，这给应用适用于中型语言模型的量化方法带来了挑战。系统异常值[43]就是大型语言模型激活值的一种独特属性，阻碍了此类方法直接用于大型语言模型的仅权重量化。

一些工作对大型语言模型直接应用均匀、四舍五入到最接近的量化方法，并进行了一些小的修改[14,21,50]。ZeroQuant - V2 [21]对OPT和BLOOM进行量化。研究表明，使用16比特激活值并直接将这些模型的权重量化为8比特整数（采用行对称量化）会导致可忽略的困惑度下降，而仅4比特权重量化则会导致显著的性能下降。为了进一步挑战低比特量化的极限，ZeroQuant - V2 [21]提出了低秩补偿（LoRC）方法，该方法使用存储高效的低秩矩阵\(\hat{E}\)来近似原始权重矩阵\(W\)和量化权重矩阵\(\hat{W}\)之间的误差\(E\)，使得\(\hat{W}+\hat{E}\)能更好地近似原始权重\(W\)。然而，Zeng等人[14]发现GLM - 130B可以直接使用行对称量化将权重量化为4比特，且在LAMBADA数据集上的零样本准确率评估中性能下降可忽略不计。作者将GLM - 130B具有吸引人的4比特量化属性归因于其权重分布比GPT风格的模型（如OPT和BLOOM）更规整，没有那么多偏斜。

另一类研究在大型语言模型的仅权重量化中考虑非均匀方法。关键的见解在于，训练后大型语言模型的权重分布是非均匀的，所以让公式(4)中的区间\([\Delta_{i}, \Delta_{i+1})\)也非均匀，有助于将量化推进到更低的比特宽度。LUT - GEMM [51]（也称为nuQmm）扩展了一种非均匀量化方法，即二进制编码量化（BCQ）[52]，它将全精度参数分解为二进制参数和一组单独的缩放因子。

作者在传统BCQ方法中添加了一个偏差项以增加表示能力，并使用组粒度量化在压缩比和模型性能之间进行权衡。SqueezeLLM [49]验证了大型语言模型推理受内存限制，与其他神经网络相比算术强度极低。此外，SqueezeLLM采用基于灵敏度的k - 均值质心作为非均匀量化的量化权重值（见公式(5)中的\(X_{i}\) ）。基于灵敏度的k - 均值方法将权重的海森矩阵近似为灵敏度，突出了最小化对海森值较大的权重的扰动的重要性。SqueezeLLM比标准均匀量化方法具有更好的困惑度，同时与FP16基线相比实现了约2倍的加速。Dettmers等人[48]提出了一种新的NormalFormat（NF）数据类型，也可视为非均匀量化。NF数据类型基于分位数量化[53]，这是一种信息论上最优的数据类型，可确保每个量化区间从输入张量中分配到相等数量的值。作者利用预训练神经网络权重通常具有以零为中心、标准差为\(\sigma\)的正态分布这一特性，因此可以通过缩放\(\sigma\)将其归一化到标准正态分布\(N(0,1)\) 。k比特的NormalFormat对标准正态分布\(N(0,1)\)使用k比特分位数量化来找到其量化值\(Q_{i}\) （\(Q_{i}\)的定义见公式(5)）。在实践中，要量化的权重被重新缩放到范围\([-1, 1]\) ，然后四舍五入到最接近的量化值\(X_{i}\) ，即采用四舍五入到最接近（RTN）方法。

上述是零样本方法，仅考虑最小化原始权重矩阵\(W\)和量化权重矩阵\(Q(W)\)之间的差异，即最小化权重矩阵的量化误差\(argmin_{\hat{w}}|| W-Q(W) \|\) 。然而，考虑到神经网络的高度非线性，权重空间中的小距离并不一定意味着原始模型和量化模型的输出差异也小。因此，如果给定一小组典型示例\(C\)（称为校准集），则有一些单样本方法[41,42,54,55]考虑优化原始层和量化层的输出激活之间的差异：
\(argmin_{\hat{w}}\| X W-X Q(W)\| for X \in C\)

大型语言模型仅权重量化的单样本方法的一个典型工作是GPTQ（也称为OPTQ）[42]，它基于一种称为最优脑量化（OBQ）[56]的自适应舍入方法。OBQ独立处理权重矩阵的每一行，一次量化一个权重，同时更新所有尚未量化的权重以补偿量化单个权重所产生的误差。然而，OBQ并非专门为大型语言模型设计，在实践中可能速度较慢且不准确。为了解决这些问题，GPTQ并行量化所有权重行以提高效率，使用延迟批量更新在量化过程中实现更高的计算与内存比，并使用Cholesky重写来帮助提高数值稳定性。通过这些修改，GPTQ可以在单个NVIDIA A100 GPU上约4小时内对OPT - 175B或BLOOM - 176B进行量化。此外，GPTQ在极端量化（将权重量化到2比特或更低）下仍能提供合理的精度。QuIP [55]定义了一类自适应舍入方法来优化公式(7)，并在预定义的方法族中定义了最优方法，称为LDLQ。LDLQ使用校准集中向量的二阶矩矩阵的LDL分解来找到更新尚未量化权重的最优方法。作者表明GPTQ是LDLQ的一个特殊情况。此外，QuIP提出了非相干处理，可将权重矩阵转换为更适合量化的形式。结合LDLQ和非相干处理，QuIP是第一个在2比特仅权重量化上取得可行结果的大型语言模型量化方法。AWQ [41]表明，仅保留FP16中与显著激活对应的0.1%通道，并对其余权重矩阵进行量化，有助于显著提高模型性能，这意味着权重并非同等重要。此外，AWQ旨在在不使用混合精度的情况下减少关键权重的量化误差，这通过激活感知缩放来实现，该方法通过与公式(7)类似的目标自动找到每个（输入）通道的缩放比\(s\) ，即\(argmin_{s}\left\|(s^{-1} \cdot X) Q(W \cdot s)-X W\right\|\) ，使得具有高缩放因子的显著权重能够得到更好的表示，而不显著的权重也不会被忽略。OWQ [57]是对OPTQ的改进，显著提高了量化模型的质量。它使用混合精度量化方案，对易受激活异常值影响的权重应用更高的精度。敏感权重通过类似于[49]的基于灵敏度的方法来识别。

也有一些研究关注量化中的舍入标准。SignRound [58]指出，随着量化比特宽度的减小，量化网格变宽，因此强调了向上和向下舍入的重要性。它扩展了先前的工作[59]，使用带符号梯度下降来学习权重舍入，并且可以在400次优化步骤内取得良好的结果。

 3.3.2 权重+激活值量化

对大型语言模型的权重和激活值都进行量化是一个具有挑战性的问题，原因如下：第一，激活值的范围和统计信息直到实际运行时才知道；第二，对权重和激活值进行量化能够在特定硬件上实现高效的低比特数据类型运算；第三，大型语言模型激活值中出现的系统异常值对模型性能至关重要，在量化过程中不应被裁剪。虽然前两个原因适用于所有模型，但第三个原因是大型语言模型所特有的，将针对大型语言模型的方法与先前模型的方法区分开来。

与仅权重量化类似，权重+激活值量化也可以使用基本的均匀量化方法[21,43,44,63]，但需要特别注意激活值中的异常值。LLM.int8() [43]强调随着模型规模的扩大，大型语言模型激活值中会出现极端异常值。作者表明这些异常值具有高度系统性。给定线性层的输入激活\(X_{f 16} \in \mathbb{R}^{N ×D_{in }}\) ，异常值几乎在序列中的所有\(N\)个标记中系统地出现，但它们仅限于特定的特征/隐藏维度\(\hat{d} \in{1,2, ..., D_{in }}\) 。因此，LLM.int8()提出分离异常值特征维度\(O={\hat{d} | \hat{d} \in \mathbb{Z}, 1 ≤\hat{d} ≤D_{in }}\) ，该集合包含所有至少有一个激活异常值且幅度大于阈值\(\alpha\)的特征维度\(\hat{d}\) 。异常值维度以高精度数据类型（如FP16）保留，而平均值则使用对称均匀量化为低精度数据类型（如INT8）。用爱因斯坦记号表示，矩阵乘法变为：
\(X_{f16}W_{f16} \approx \sum_{\hat{d} \in O} X_{f16}^{\hat{d}}W_{f16}^{\hat{d}} + S_{f16} \cdot \sum_{d \notin O} X_{i8}^{d}W_{i8}^{d}\)(8)
其中\(S_{f16}\)是反量化因子。异常值维度的数量\(|O|\)非常小，所以这种分解通常只会消耗超过0.1%的额外内存。与将异常值分离到一个额外矩阵不同，RPTQ [63] 提出基于激活\(X \in \mathbb{R}^{N×D_{in}}\)各维度的最小值和最大值\((X_{min, i}, X_{max, i})\)对其维度进行聚类和重新排序。其思路是将包含异常值的维度归为同一簇，并进行簇级量化。需要注意的是，每个激活维度的统计信息是在校准集上测量的，这样在推理前就可以完成聚类以找到维度的新顺序。为了进一步减少延迟，RPTQ将重新排序操作与其他操作融合：1）与LayerNorm操作结合，避免额外的数据移动和调整；2）对权重\(W\)的列进行重新排序，以对输出\(Y = XW\)的维度进行重新排序。

最近，低比特浮点格式（如FP4、FP8）作为大型语言模型量化的有前景的替代方案出现[64,65,66]。尽管FP8格式可能具有更高的硬件成本，但它得到了NVIDIA等领先硬件供应商的支持。直观地说，低比特FP格式可以看作是非均匀量化的一种特殊情况，它为小数值提供了通常更广泛的数据范围和更高的精度，但对大数值的精度较低。FP格式的这种特性有助于解决激活中的异常值问题。MoFQ（混合格式量化）[64]和ZeroQuant - FP [65]都表明，在激活量化方面，FP8量化始终优于INT8。MoFQ进一步提供了一种算法，根据张量误差、层输出误差或模型输出误差，从一些候选格式（INT4、INT8、FP4、FP8）中为每一层确定最佳数据格式。此外，MoFQ将标准FP格式中的特殊NaN（非数字）和Inf（无穷大）值重新分配为归一化数字，以增强并让FP格式表示更多的值，这对于像FP4这样的低比特格式尤为重要。ZeroQuant - FP将权重和激活都量化为FP格式。对于使用FP4权重和FP8激活的情况，ZeroQuant - FP提出了一种位移动方法，将FP4转换为FP8以有效提高推理效率。

另一种有前景的方法是抑制激活维度中出现的异常值[45,67,68,69,70]。其基本思想是，我们可以将激活中的异常值维度按因子\(s_{i}\)缩小，并将权重矩阵中相应的维度按因子\(S_{i}\)放大，而不改变层的输出：
\(Y = XW = (\hat{X} diag(s)) \cdot (diag(s)^{-1} \hat{W}) = \hat{X} \hat{W}\)
这样缩放后的激活\(\hat{x}\)将更适合量化。SmoothQuant [45]使用以下公式计算每个维度的缩放因子：
\(s_{i} = max(|X_{i}|)^{\alpha} / max(|W_{j}|)^{1 - \alpha}\)
其中\(\alpha\)是一个超参数，用于控制从激活到权重转移的难度程度。Outlier Suppression [67]发现LayerNorm中的\(\gamma\)起到了异常值放大器的作用。因此，它提出了Gamma Migration方法，使用前一层的\(\gamma^{-1}\)作为缩放因子\(s\)。Outlier Suppression+ [68]通过引入额外的偏移因子\(z\)扩展了该方法：
\(\begin{aligned} Y &= XW = (\hat{X} diag(s) + z) \cdot (diag(s)^{-1} \hat{W}) \\ &= \hat{X} \hat{W} + zW = \hat{X} \hat{W} + \hat{b} \end{aligned}\)
每个维度的偏移因子计算为\(z_{i} = (max(X_{i}) + min(X_{i})) / 2\)，这有助于消除激活\(\hat{X} = (X - z) diag(s)\)中的不对称性。FPTQ [69]提出了一种新的离线对数激活均衡（LAE）方法，以非线性方式调节激活分布，每个通道的缩放因子\(s\)计算为：
\(s_{i} = max(|X_{i}|) / log_{2}(2 + max(|X_{i}|))\)
虽然上述方法使用手工制作的量化参数（如缩放因子\(s\)），但Outlier Suppression+则通过使用校准集优化以下目标来寻找最优缩放因子\(s\)：
\(min _{s} \mathbb{E}[\| XW - (Q(\hat{X})Q(\hat{W})+\hat{b})\| _{2}^{2}]\) (13)
此外，OmniQuant [70]提出学习裁剪范围\([\alpha, \beta]\)来调节权重的极值。QLLM [71]提出了一种独特的处理激活中异常值的方法。该技术涉及自适应通道重组过程，将异常值通道分割为多个子通道，以确保激活幅度的分布更加均匀。该过程还会合并相似的通道，以保持原始通道数量，提高效率。

也有一些近期研究采用了不属于上述任何一类的方法，为了完整性，我们在此简要介绍。REx [72]对量化误差\(W - Q(W)\)进行量化，以使原始值和反量化值之间的量化误差更小，这是以效率换取更高的模型性能。OilVe [73]采用了异常值 - 受害者对（OVP）机制，该机制会修剪一些量化后的低精度正常值，为高精度异常值腾出额外空间。

作为大型语言模型量化PTQ方法的总结，我们在此简要比较和对比仅权重量化和权重 + 激活值量化方法。一方面，仅权重量化方法可以将量化极限推进到更低的比特宽度（甚至低至3比特或2比特），这显著减少了大型语言模型所需的设备内存大小，因为模型权重占用了大部分内存。另一方面，权重 + 激活值量化可以利用特定硬件支持的高效低比特算术带来的额外加速，并且在推理过程中不会引入额外的反量化开销。然而，这些方法通常需要更高的比特宽度（约8比特）来存储权重和激活值。仅权重量化和权重 + 激活值量化方法都有各自的优缺点，并且都是具有巨大潜力和需求的活跃研究方向。

 3.4 大型语言模型的量化感知训练

量化感知训练（QAT）是一种重新训练量化模型以弥补量化导致的性能下降的方法。如前所述，在大型语言模型出现之前，针对其他模型（如CNN、中型语言模型）的QAT已取得显著成功。然而，这类方法通常涉及对整个模型进行全参数重新训练，这对大型语言模型来说成本过高，因此也有一些尝试将量化与参数高效训练方法相结合，以显著降低大型语言模型上QAT的成本。

因此，我们将当前大型语言模型上的QAT方法分为两类：全参数重新训练和参数高效重新训练。我们将在以下部分分别讨论这两类工作。

 3.4.1 全参数重新训练

在大型语言模型中使用QAT框架的主要关注点是在较小的数据集上重新训练它们，同时不损害其涌现能力，如上下文学习能力。当前的方法通常将QAT和蒸馏相结合，以保留原始（教师）模型的这些能力[74,75]。

LLM - QAT [46]直接将基本的QAT框架[24]应用于大型语言模型。为了解决这个问题，LLM - QAT提出使用无数据蒸馏方法，即使用原始大型语言模型生成数据，并训练量化的大型语言模型以匹配原始大型语言模型在生成数据上的输出分布。此外，LLM - QAT还实现了对键值缓存的量化和QAT，键值缓存在长句生成过程中占用大量内存。

为了减轻重新训练整个大型语言模型的高昂成本，ZeroQuant [21,44,65]提出了一种逐层知识蒸馏方法。该方法使用原始大型语言模型作为教师模型，并逐层处理大型语言模型的权重。假设大型语言模型有\(N\)层\(L_{1}, L_{2}, ..., L_{N}\)，有一些输入数据集\(X\)，\(L_{k}\)的量化版本为\(Q(L_{K})\)。在对层\(L_{1}, L_{2}, ..., L_{k - 1}\)进行QAT和蒸馏后，我们使用以下损失来更新\(L_{k}\)：
\(\mathcal{L}_{k} = MSE(L_{k} \cdot L_{k - 1}...L_{1}(X) - \hat{L_{k}} \cdot L_{k - 1}...L_{1}(X))\) (14)

 3.4.2 参数高效重新训练

有许多工作使用参数高效方法（如LoRA、Adapter、Prompt Tuning）来微调大型语言模型，这些方法将在附录A中讨论。在本节中，我们讨论一些在QAT的重新训练过程中使用参数高效方法的方法。

典型的工作[47,48,62,71,76,77,78]采用低秩适应（LoRA）在相对可接受的计算预算内重新训练量化的大型语言模型。QLoRA [48]将大型语言模型的权重量化为4比特NormalFormat，随后采用带有16比特BrainFloat的LoRA在下游任务上使用交叉熵损失微调量化模型。它还引入了一种名为双重量化的技术，对量化参数进行量化，以在牺牲计算速度的情况下进一步压缩模型大小。结合所有这些技术，QLoRA能够在具有30G内存的GPU上高效微调650亿参数的大型语言模型。在QLoRA之后，QA - LoRA [78]提出将组粒度量化集成到QLoRA中。作者认为QLoRA中的量化参数比LoRA参数少得多，导致量化和低秩适应之间的不平衡，而组粒度操作可以通过增加量化参数的数量和减少适应参数的数量来缓解这个问题。此外，LoftQ [62]发现QLoRA中LoRA矩阵的零初始化对下游任务效率不高。相反，LoftQ提出使用原始权重和量化权重之间的差异\(W - Q(W)\)的奇异值分解（SVD）来初始化LoRA矩阵。LoftQ在量化和SVD之间交替进行，以获得对原始权重的更好近似。LACos - BLOOM [76]使用8比特块均匀量化对模型权重进行量化。然后使用可扩展的LoRA和8比特Adam优化器对量化模型进行微调。INT2.1 [47]利用GPTQ将大型语言模型量化为INT2，并发现量化模型的行为与原始全精度模型有显著偏差。INT2.1将额外的可训练参数（LoRA矩阵）集成到模型中，并仅更新占总参数5%的LoRA矩阵。训练目标结合了从全精度模型到量化模型的缩放Kullback - Leibler散度和交叉熵损失，以鼓励准确的下一个标记预测。他们的实验表明，使用LoRA微调的INT2大型语言模型可以生成语言连贯的英语文本，并遵守规定的指令。

其他工作[79,80]冻结量化索引，仅微调量化参数（如均匀量化中的缩放因子\(S\)和非均匀量化中的量化级别\(\Delta_{i}\) ）。AlphaTuning [79]采用二进制编码量化[52]。在适应阶段，所有任务的二进制值都被冻结，而缩放因子则针对下游任务进行微调。PEQA [80]使用均匀量化将语言模型的每个全连接层量化为低比特整数矩阵和标量向量。随后，针对每个下游任务对标量向量进行微调。

也有工作将量化与Adapters [81]和Prompt Tuning [82]相结合。

 3.5 大型语言模型量化的其他主题

一些与量化相关的工作无法归类为PTQ或QAT，我们在本节中讨论这些工作。

一个重要的主题是与量化算法共同设计高效内核[83,84]、设计硬件友好的量化方法[85,86]以及将量化方法集成到实际应用中[87,88,89,90,91]。LUT - GEMM [51]是为BCQ方法[52]的扩展版本设计的高效内核，它可以表示均匀和非均匀量化。由于在BCQ中权重由二进制向量和缩放因子表征，LUT - GEMM可以预先计算并在查找表（LUT）中存储全精度激活和二进制模式的所有可能组合，以避免重复计算并消除权重的反量化，与传统模拟量化相比，这将3比特量化的OPT - 175B模型的延迟加速了2.1倍。上述章节中讨论的许多均匀[21,43,44,73]和非均匀量化方法[49]也设计了特殊的内核来降低总体延迟。

其他有意义的工作研究大型语言模型量化的内在特性[92,93,94]。例如，Dettmers和Zettlemoyer [93]在16比特激活和\(3 ≤k ≤8\)比特权重、参数规模从1900万到176亿的不同大型语言模型家族（BLOOM、OPT、NeoX/Pythia和GPT - 2）上进行了广泛的实验。作者关注零样本能力和总模型比特数之间的权衡，并表明4比特精度在不同的大型语言模型类别和量化方法中几乎普遍是最优的权衡。Liu等人[94]旨在研究量化对涌现能力的影响，涌现能力是区分大型语言模型和小型语言模型的重要特征。他们的实证实验表明，4比特量化模型中仍然存在涌现能力，而2比特模型在这些能力的测试中遇到严重的性能下降。作者进一步对提高极低比特模型的性能进行了详细实验。

一些工作[67,95,96]也专注于研究大型语言模型中系统异常值出现的原因，并寻找从源头上抑制异常值的方法。Quantizable Transformer [95]将激活中的异常值归因于注意力头试图不更新残差的行为。作者相应地设计了裁剪后的softmax和门控注意力机制，使模型能够在不产生异常值的情况下生成注意力函数的最小幅度（甚至精确为零）输出。Outlier suppression [67]则将LayerNorm中的\(\gamma\)视为异常值的有害放大器。目前关于激活异常值的来源尚无共识。然而，Ahmadian等人[96]发现异常值维度可能不像先前工作[43]认为的那样是模型规模的固有产物，而是对预训练期间的优化条件（如丢弃率、权重衰减、数据类型）敏感。

 4 剪枝

作为一种用于神经网络压缩和加速的传统技术，剪枝从模型中去除非必要的权重或结构，同时将网络的性能保持在与原始状态近乎相同的水平。尽管剪枝在CNNs [97]中取得了显著成果，但与量化和蒸馏等其他压缩技术相比，其在大型语言模型中的有效性较弱。剪枝效果不佳的原因在于微调过程。由于模型参数数量众多，微调成本高昂，使得剪枝难以充分发挥其效果。尽管如此，剪枝仍是模型压缩的关键技术，需要进一步探索以提高和优化其在大型语言模型中的效果，从而获得更好的结果。

在以下部分，我们将在4.1节中概述剪枝方法和基本概念。随后，在4.2节中，我们将阐述针对中型语言模型（即参数在数十亿级别的模型）的剪枝技术，因为它们与大型语言模型在结构上具有相似性。4.3节将深入探讨专门为大型语言模型设计的剪枝方法。最后，在4.4节中，我们将介绍一些虽不属于剪枝方法但与剪枝相关的辅助技术，以提高大型语言模型剪枝的效果，然后讨论大型语言模型剪枝领域未来发展面临的挑战。

 4.1 基本概念

剪枝的分类标准众多。然而，其中最重要的是两个基本问题：剪什么和怎么剪。这两个问题的答案分别对应于剪枝单元和剪枝度量。我们将介绍这两个基本概念以及其他一些基本概念。
1. 剪枝单元：剪枝的第一个基本问题是应该修剪哪种元素。剪枝单元指的是剪枝过程中的最小修剪元素，包括权重、神经元、注意力头、层等元素。基于剪枝单元，剪枝方法可大致分为非结构化剪枝和结构化剪枝。在非结构化剪枝中，剪枝单元聚焦于单个权重，将待剪枝的权重归零。而在结构化剪枝中，剪枝单元涵盖更广泛的网络结构，如神经元、注意力头和层，要剪枝的结构会从网络中移除。

非结构化剪枝由于不受网络结构限制，可以对单个权重进行剪枝，因此往往能获得更高的稀疏率并保持更好的性能。然而，权重矩阵的不规则稀疏模式源于非系统性出现的零值，其计算效率与密集矩阵几乎相当。因此，非结构化剪枝在实现显著的推理加速方面并不常见。

结构化剪枝通过修剪网络结构（如注意力头、前馈网络（FFN）神经元和隐藏维度），易于实现推理加速。但不可避免的结构删除可能会导致模型性能下降。为避免模型崩溃，结构化剪枝模型的稀疏率低于非结构化剪枝模型。

形式上，在剪枝过程中通常会用一个二进制掩码\(z\)覆盖剪枝单元，并在剪枝后与模型相乘。对于非结构化剪枝，剪枝过程可以定义为一个约束优化问题：
\(\min_{w, z} \mathcal{L}(w \odot z ; \mathcal{D}) = \min_{w, z} \frac{1}{N} \sum_{i = 1}^{N} \ell(w \odot z ;(x_{i}, y_{i}))\)
\(\text{s.t. } \| z\| _{0} \leq t\)
其中\(\odot\)表示元素相乘，\(w = \{w_{1}, w_{2}, \ldots, w_{M}\}\)是网络权重，\(\mathcal{D}\)是由\(N\)个输入\(x_{i}\)和输出\(y_{i}\)对组成的数据集，\(t\)是目标非稀疏率（即\(1\)减去稀疏率）。类似地，结构化剪枝的过程如下：
\(\min_{w, z} \mathcal{L}(s \odot z ; \mathcal{D}) = \min_{w, z} \frac{1}{N} \sum_{i = 1}^{N} \ell(s \odot z ;(x_{i}, y_{i}))\)
\(\text{s.t. } f(z ; s) \leq t\)
其中\(s = \{s_{1}, s_{2}, \ldots, s_{K}\}\)是由\(w\)组成的剪枝结构，\(f(\cdot)\)是根据二进制掩码和结构计算非稀疏率的函数。
2. 剪枝度量：剪枝的第二个基本问题是如何确定一个元素是否重要，是否应该被剪枝。剪枝度量就是这个问题的答案。剪枝度量是识别剪枝单元重要性的标准，大致可以分为三类：基于幅度的、基于损失的（即考虑属于剪枝单元的权重的一阶和二阶导数信息）和正则化。

基于幅度的剪枝方法将权重和激活值的幅度（即绝对值）作为剪枝度量的一部分。这类方法的基本原理是，剪枝单元的权重幅度或激活值直观地反映了其重要性。仅权重的幅度就可以作为一种剪枝度量，构成了一种著名的基础剪枝方法，称为幅度剪枝[98]。幅度剪枝是基于幅度的基本剪枝方法。在这种方法中，设置一个阈值，将幅度较小的权重归零，阈值通常由稀疏率推导得出。尽管重要性分数的定义具有一定的启发式，但幅度剪枝在各种模型中都显示出了有效性。

除了直观的基于幅度的度量，还有一种更复杂的度量是基于损失的度量。基于损失的度量旨在将剪枝单元的重要性归因于其对损失的影响。如果修剪一个元素后损失显著增加，则表明该元素不应被剪枝。更准确地说，修剪一个元素后损失增加得越大，该元素的重要性就越高。然而，逐个检查修剪单个元素后的损失是资源和时间密集型的。相比之下，使用泰勒展开提供了一种更方便快捷的方法来阐明损失的变化。修剪后的损失变化可以使用泰勒展开进行量化，纳入剪枝单元对损失的一阶或二阶导数，通常忽略更高阶导数。与逐个评估修剪每个元素后的损失这种资源和时间密集型的方法相比，计算一阶和二阶导数是一种更高效、更节省时间的替代方法。

此外，正则化方法包括\(L_{0}\)、\(L_{1}\)和\(L_{2}\)正则化。虽然\(L_{1}\)正则化以诱导权重稀疏性而闻名，但在剪枝的背景下，\(L_{0}\)正则化是更常用的正则化方法。
3. 动态/静态剪枝：为了增强对不同输入的适应性，一种称为动态剪枝的剪枝方法根据特定的输入特征构建网络。我们将在第7节中讨论这些内容。相比之下，静态剪枝方法在训练时对模型进行剪枝，并在剪枝后固定架构，因此不同的输入共享相同的剪枝网络。静态剪枝方法根据剪枝时期可分为预训练剪枝、训练中剪枝和训练后剪枝，如图3所示。
    预训练剪枝：首先对初始化的网络进行剪枝，然后训练稀疏网络。
    训练中剪枝：同时训练和剪枝密集网络，其中正则化方法是典型代表。
    训练后剪枝：是最常用的剪枝流程类型，对训练好的密集网络进行剪枝以获得稀疏网络，通常遵循我们之前提到的训练、剪枝和微调范式。

图3：三类静态剪枝方法。(a) 预训练剪枝；(b) 训练中剪枝；(c) 训练后剪枝
4. 迭代/一次性剪枝：由于剪枝不可避免地会损害模型性能，一种常见的剪枝流程范式包括三个步骤：训练、剪枝和微调，如图3(b)、(c)所示。第一步是训练网络以确定各个剪枝单元的重要性。随后，第二步通过剪枝去除非必要的剪枝单元，第三步则专注于微调以恢复剪枝后模型的性能。

鉴于微调过程可能会使最初归零的权重变为非零，最后两步需要迭代重复，直到达到目标稀疏率。这种迭代设计强调每次剪枝步骤之后都有一个微调步骤，从而有助于保持模型的性能。包含迭代剪枝和微调轮次的方法被归类为迭代剪枝。

然而，随着模型参数变得越来越大，迭代剪枝和微调过程成本高昂且耗时。因此，更多的剪枝方法倾向于仅对网络进行一次剪枝以达到目标稀疏率，放弃迭代剪枝和微调轮次。这些方法被归类为一次性剪枝。
5. 全局/局部剪枝：早期的剪枝方法通过比较所有剪枝单元来识别和消除那些不太重要的单元。由于这些方法的比较范围涵盖整个网络，因此被归类为全局剪枝方法。然而，全局剪枝允许各个局部区域具有不同的稀疏率，这可能会导致特定区域（如一层、一列）过度剪枝，对模型的整体性能产生显著影响。解决这个问题的方法是应用局部剪枝方法。局部剪枝对每个区域的稀疏性施加约束，确保每个区域内的稀疏率不会达到过低的阈值，从而降低模型崩溃的风险。
6. 数据驱动/无数据剪枝：剪枝方法分为数据驱动和无数据两种模式，这区分了剪枝决策对数据的依赖程度。具体而言，数据驱动的剪枝方法（大多数剪枝技术都是这种类型）根据可用数据做出剪枝决策。相反，无数据剪枝方法（如幅度剪枝[98]）独立于数据输入执行网络剪枝。一般来说，数据驱动的剪枝方法由于依赖数据驱动的见解，往往表现出更好的性能，而无数据剪枝方法虽然效果较差，但不依赖数据。
7. 上游/下游剪枝：语言模型的训练涉及两个主要阶段——预训练和微调。剪枝方法可以根据应用的时间进行分类。被确定为上游剪枝的技术是在微调阶段之前对模型进行剪枝。相比之下，下游剪枝方法的特点是在微调过程中同时执行剪枝。因此，上游剪枝保留了剪枝后模型对多个任务的适应性，确保了其通用性。相反，下游剪枝使剪枝后的模型专注于一个特定的、定义明确的任务。

 4.2 中型语言模型的剪枝方法

像GPT - 2和BERT这样的语言模型最初在大规模语料库上进行训练，并在微调后适用于各种下游任务。具体而言，语言模型的剪枝在三个关键方面与卷积神经网络（CNNs）或循环神经网络（RNNs）的剪枝方法不同。首先，语言模型的参数数量远远超过CNNs或RNNs。例如，BERT - large模型包含3.35亿个参数，而典型RNN的参数数量在数千万级别[99]。参数数量的增加放大了微调阶段的时间和计算需求。因此，语言模型的剪枝需要应对这种大量参数带来的挑战。其次，语言模型有潜力针对多种下游任务进行微调。某些上游剪枝方法需要保留语言模型作为多任务求解器的能力。第三，基于Transformer的语言模型具有截然不同的结构组成。因此，鉴于模型的架构，某些结构化剪枝方法可能需要重新配置以适应模型的结构。总之，存在专门为语言模型设计的剪枝方法，以适应它们的独特特征，与传统的剪枝方法有所不同。

我们将在下面介绍这些针对中型语言模型的剪枝技术，包括专门为基于Transformer的模型设计的方法以及适用于多种不同架构模型的通用方法。考虑到剪枝方法的基本特征（即确定剪什么和怎么剪），我们将按照剪枝单元和度量的顺序介绍这些剪枝方法。首先，我们将剪枝方法分为两个主要部分：非结构化剪枝和结构化剪枝。随后，根据剪枝标准的顺序，我们将详细阐述三种剪枝方法：基于幅度的剪枝、基于损失的剪枝和正则化。

 4.2.1 中型语言模型的非结构化剪枝

非结构化剪枝方法在没有任何特定约束的情况下将非必要的权重归零。我们将根据具体的度量系统地介绍中型语言模型的非结构化剪枝方法，包括基于幅度的剪枝、基于损失的剪枝和正则化。
1. 基于幅度的剪枝：基于幅度的剪枝方法以其简单性和有效性而著称，将权重和激活值的幅度纳入剪枝度量中。在本节关于中型语言模型基于幅度的剪枝中，我们发现所有相关方法都只关注权重的幅度。因此，我们将介绍这些基于权重幅度的剪枝方法。

幅度剪枝[98]是最常用的剪枝方法，已在中型语言模型的背景下进行了研究[100,101,102,103]。Gordon等人[100]通过幅度剪枝对BERT的压缩进行了研究。结果表明，大约30 - 40%的权重是非必要的，可以在不影响BERT性能的情况下丢弃。此外，针对特定任务对BERT进行微调并不能提高最终可实现的稀疏率。这意味着BERT可以在预训练阶段进行一次剪枝，无需为每个任务单独进行剪枝，同时保持性能完整。基于此，“一次剪枝适用于所有任务”（Prune Once for All）[104]方法在微调之前对模型进行一次剪枝，以适用于所有任务。

幅度剪枝通过直接将模型的稀疏率剪枝到目标比率，可能会导致模型性能大幅下降。与幅度剪枝相比，渐进式幅度剪枝（Gradual Magnitude Pruning，GMP）[105]引入了一个稀疏率调度，在剪枝过程中逐渐降低稀疏率。“一次剪枝适用于所有任务”[104]和GMP⋆[106]都是GMP在语言模型剪枝中的具体应用。此外，GMP⋆引入了一个初始的大幅剪枝步骤，以更好地适应高目标稀疏率（如97%）。这种方法在后续的剪枝步骤中提供了更多的恢复时间，最终提高了性能，优于包括“一次剪枝适用于所有任务”[104]在内的大多数剪枝方法。
2. 基于损失的剪枝：虽然基于幅度的剪枝易于实现，但在某些情况下，幅度本身可能无法准确反映权重的重要性。某些权重的幅度可能较小，但它们的贡献仍然至关重要[107]。因此，一种更科学合理的方法是在特定任务的背景下评估这些权重。本节中的方法采用了针对中型语言模型的基于损失的剪枝策略。这些方法基于性能进行更细致的评估。鉴于模型的训练过程本质上是为了最小化损失，损失无疑是衡量模型性能最可靠的指标。

第一类主要的基于损失的剪枝方法在特定度量中整合了梯度信息。这些方法评估权重重要性的通用表达式可以通过负梯度 - 权重乘积来表示，如下所示：
\(I = -w \nabla \mathcal{L}(w)\) (17)
对这个表达式的第一种解释与权重变化有关。权重的负梯度方向表示权重想要增加的方向。因此，如果权重方向与权重增长方向一致，则表明该权重在特定任务中的重要性，因为任务需要其幅度继续增加。或者，这个表达式的第二种解释可以简单地看作是损失变化的泰勒展开的一阶项，忽略了更高阶项。

许多方法基于这个通用表达式进行了改进。移动剪枝（Movement Pruning）[108]累积了负梯度 - 权重乘积的多次更新。累积这些信息有助于在剪枝过程中最小化波动。在一阶方法中，移动剪枝是一种开创性的方法，在此基础上发展了许多扩展方法[109,110]。为了减轻小批量采样和复杂训练动态带来的巨大可变性和不确定性，PLATON [111]采用了一种权重剪枝策略，考虑了单个权重的重要性和不确定性。不确定性源于重要性的变化。为了提高稳定性，对重要性和不确定性都进行指数移动平均。每个权重的最终重要性得分由平滑后的重要性和不确定性的乘积确定。参数高效稀疏训练（Parameter - efficient Sparse Training，PST）[112]和LoRAPrune [113]将权重的幅度和累积的负梯度 - 权重乘积相加，以得出最终的重要性得分。

第二类主要的基于损失的剪枝方法在特定度量中整合了二阶导数信息。当使用泰勒展开并展开到二阶项（忽略更高阶项）时，损失的变化可以表示如下：
\(\begin{aligned} \mathcal{L}(w) - \mathcal{L}(w^{}) & \simeq (w - w^{})^{\top} \nabla \mathcal{L}(w^{}) \\ & + \frac{1}{2}(w - w^{})^{\top} H_{\mathcal{L}}(w^{})(w - w^{}) \end{aligned}\)
其中\(H_{L}(w^{})\)是海森矩阵。这些方法是训练后剪枝方法，总是对训练良好的网络\(w^{}\)进行剪枝。因此，可以忽略梯度\(\nabla L(w^{})\)，得到表示权重重要性的通用表达式：
\(I = \frac{1}{2}(w - w^{})^{\top} H_{\mathcal{L}}(w^{})(w - w^{})\)

早期工作中的最优脑损伤（Optimal Brain Damage，OBD）[114]和最优脑外科医生（Optimal Brain Surgeon，OBS）[115]代表了二阶剪枝方法。它们都利用损失函数的海森矩阵来选择性地消除特定参数，同时最小化对损失的影响。为了简化计算，这两种方法都在一定程度上简化了海森矩阵的计算。然而，OBD仅计算海森矩阵的对角元素，而OBS还考虑了非对角元素的影响。这些方法为随后的许多方法提供了灵感。最优BERT外科医生（Optimal BERT Surgeon）[116]将OBS的原理扩展到BERT的背景下，与一些基于幅度的剪枝方法[98,104,106]和一阶剪枝方法[108,111]相比，取得了更好的结果。
3. 正则化：除了上述方法，正则化技术在中型语言模型中也有许多应用。\(L_{1}\)和\(L_{2}\)正则化是常用的用于应对网络过拟合的方法。它们都在损失函数中引入了一个正则化项。此外，\(L_{1}\)正则化还有诱导权重稀疏性的额外效果。然而，在直接对网络进行剪枝时，\(L_{1}\)正则化并不总是最合适的选择。这是因为\(L_{1}\)正则化对较大的权重施加了更大的惩罚，偏离了消除不重要连接的原始剪枝目标，而较小的权重往往位于这些不重要的连接中。

相反，\(L_{0}\)正则化[117]是一种比\(L_{1}\)和\(L_{2}\)正则化更通用的剪枝方法。\(L_{0}\)正则化将权重的\(L_{0}\)范数纳入损失函数。与\(L_{1}\)和\(L_{2}\)正则化类似，\(L_{0}\)正则化对非零权重进行惩罚。然而，它的独特之处在于对所有非零权重施加相等的惩罚，这与公平惩罚所有现有连接的剪枝目标完全一致。

所有这三种正则化方法在剪枝过程中的训练目标可以用以下公式表示：
\(\min_{w, z} \frac{1}{N} \sum_{i = 1}^{N} \ell(w \odot z ;(x_{i}, y_{i})) + \lambda\| w\| _{p}\) (20)
其中\(\lambda\)表示正则化因子，\(\|w\|_{p}\)表示权重的\(L_{p}\)范数，\(z\)是一个二进制掩码，表示权重是否被剪枝。因此，权重的\(L_{0}\)范数可以等效地表示为二进制掩码的总和，即\(\|w\|_{0}=\sum_{i = 1}^{M} z_{i}\)。

然而，\(z\)的离散性给基于梯度的高效优化带来了挑战。为此，硬 Concrete分布被用作二进制掩码的近似，将大约一半的概率质量分配给\(\{0, 1\}\)，另一半分配给区间\((0, 1)\)，从而用连续的概率质量连接离散值0和1，如图4所示。硬 Concrete分布的公式如下：
\(\begin{aligned} & u \sim \mathcal{U}(0,1) \\ & s = Sigmoid((\log u - \log (1 - u) + \log \alpha) / \beta\[\begin{aligned}
&u \sim \mathcal{U}(0,1)\\
&s = Sigmoid((\log u - \log (1 - u) + \log \alpha) / \beta)\\
&\overline{s}=s(\zeta - \gamma)+\gamma\\
&z=\min(1,\max(0,\overline{s}))
\end{aligned}\]
其中\(u(\cdot)\)是均匀分布，\(\log \alpha\)是位置参数，\(\beta\)是温度参数，\((\gamma, \zeta)\)是“拉伸”区间，且\(\gamma < 0\)，\(\zeta > 1\)。由于重新参数化后的变量\(z\)在训练后并非严格的二进制，许多剪枝方法最后会采用一个阈值将\(z\)离散化为二进制值。对于小于阈值的\(z\)值，将其设置为\(0\)；对于大于阈值的值，将其设置为\(1\)。

虽然\(L_{0}\)正则化在剪枝中应用更广泛，但\(L_{1}\)正则化也有一些相关应用场景，并且某些方法致力于改进\(L_{1}\)正则化。例如，重新加权近端剪枝（Reweighted Proximal Pruning，RPP）[118]基于\(L_{1}\)正则化进行改进和优化。RPP包括重新加权的\(L_{1}\)正则化和近端算子。重新加权的\(L_{1}\)正则化动态地重新分配惩罚因子，对接近零的权重施加更大的惩罚。近端算子便于将稀疏模式搜索与基于反向传播的训练损失梯度更新分离，使得稀疏模式搜索更容易。
4. 其他方法：在上述讨论的非结构化剪枝方法中，许多方法即使在高稀疏率下也能保持良好的模型性能。然而，由于它们生成的稀疏矩阵具有不规则性，在实现高效推理加速方面面临挑战。为了解决这一困境，非结构化剪枝方法可以与N:M稀疏性[119]相结合。

N:M稀疏性的原理要求在神经网络中每\(M\)个连续权重的组内，非零权重的数量不超过\(N\)个。这意味着在每\(M\)个连续权重的组内，有\(N - M\)个权重为零值。因此，底层硬件可以压缩其中规则出现的零值。这种压缩依赖于硬件的独特架构，如稀疏张量核心。例如，英伟达Ampere A100配备了稀疏张量核心来加速2:4稀疏性。

对于N:M稀疏性，剪枝度量不是一个限制因素。它可以与非结构化剪枝方法无缝集成，提供纯非结构化方法可能缺乏的推理加速。例如，稀疏模式的确定可以最初基于权重的幅度[120]。作为一种通用的稀疏性方法，2:4稀疏性在不影响性能的情况下，计算速度可实现显著的两倍加速。
5. 讨论：在所有这些针对中型模型的非结构化剪枝方法中，在已进行的实验[106,116]中，最优BERT外科医生[116]相比各种基于幅度的剪枝方法[98,104,106]和一阶剪枝方法[108,111]表现出更优的性能。

尽管如此，幅度剪枝[98]仍然是应用最广泛的剪枝方法。因为它易于实现，并且与许多复杂方法相比，能取得具有竞争力的结果[121]。至关重要的是，幅度剪枝的过程独立于任何特定的数据集，从而解决了在某些可能没有数据集的场景中的挑战。

图4：通过蒙特卡罗模拟得到的硬Concrete分布的近似概率密度直方图。此硬Concrete分布的参数为\(\log \alpha = 0\)，\(\beta = 0.5\)，\(\gamma = -0.1\)，\(\zeta = 1.1\)。在这种设定下，硬Concrete分布大致将一半的概率质量分配给\(\{0, 1\}\)，另一半分配给\((0, 1)\)。

 4.2.2 中型语言模型的结构化剪枝

确实，许多非结构化剪枝方法已证明能够在保持与密集模型相当的性能水平的同时实现高稀疏率。然而，值得注意的是，非结构化稀疏模式在普通硬件上不一定能带来推理加速。因此，目前越来越多的研究集中在结构化剪枝上。

在应用于中型语言模型的结构化剪枝方法中，除了选择剪枝度量外，选择合适的剪枝单元也很重要。常用的剪枝单元包括注意力头、FFN神经元、隐藏维度等。值得注意的是，使用与模型架构相关的结构作为剪枝单元往往比使用与模型架构无关的结构（如权重块）能产生更有利的结果。

这种优越性可能归因于在减少与架构相关的结构时，保留了模型构建的基本原理。例如，在修剪注意力头后，得到的模型保留了基于Transformer模型的基本特征，只是注意力头的数量减少了。

接下来，我们将深入探讨结构化剪枝领域，包括基于幅度的剪枝、基于损失的剪枝和正则化技术。
1. 基于幅度的剪枝：直观地，对剪枝单元的权重幅度进行聚合可以作为其重要性的有意义表示，这在CNNs的卷积核中广泛适用。类似地，它也可以扩展到中型语言模型。例如，可以使用\(L_{2}\)范数对注意力头、FFN神经元[122]和权重块[123]中的权重幅度进行聚合，以表示相应的重要性。然后，根据重要性得分的顺序删除不太重要的结构。
2. 基于损失的剪枝：在基于损失的剪枝方法中，注意力头受到了大量的研究和分析[124,125,126,127]。这是因为注意力头容易变得冗余，并且其余的头通常能够承担被修剪头之前执行的功能角色。Michel等人[124]提出了一种基于头重要性得分的迭代剪枝方法。注意力头被二进制掩码变量覆盖，因此通过检查二进制掩码变量上的梯度来计算头重要性得分。结果表明，20 - 40%的Transformer头可以被修剪，而不会显著影响目标任务的测试准确率。

然而，可微子集剪枝（Differentiable Subset Pruning，DSP）[125]表明，Michel等人[124]大大低估了可以被修剪的Transformer头的数量。实验表明，DSP可以修剪高达90%的头，而不会对测试性能造成太大的下降（修剪高达90%的头意味着模型大小约缩小20%，因为头的参数只是整个模型的一部分）。DSP将Transformer头修剪视为一个子集选择问题。为了确保子集选择器的可微性，应用了Gumbel - Softmax技巧[128]及其对子集选择的扩展。结果表明，DSP在准确率和推理加速方面优于其他头修剪方法[124,129]。

除了注意力头修剪，块移动剪枝（Block Movement Pruning）[130]是一种块剪枝方法。它通过考虑任意大小的块扩展了结构化方法，并将这些结构集成到移动剪枝[108]中。模型中的矩阵被划分为固定大小的块，较大的块大小会带来更大的推理加速。此外，这种方法与FFNs中神经元的修剪相结合，可获得最佳的整体性能。同样，许多方法同时修剪FFNs中的神经元和注意力头[131,132,133,134,135,136]。

除了上述为Transformer结构设计的方法外，一些结构化剪枝方法具有通用性，因为其中的剪枝单元是神经元[137,138,139]。例如，低秩和稀疏逼近（Low - Rank and Sparse approximation，LoSparse）[137]在神经元级别（即权重矩阵的列）修剪权重矩阵。考虑到PLATON [111]中定义的参数敏感性，每个神经元的重要性由给定列内参数的累积敏感性定义。
3. 正则化：除了基于损失的剪枝方法，正则化方法是适用于中型语言模型的结构化剪枝技术的另一类。与非结构化剪枝方法不同，结构化剪枝中的正则化项涵盖与特定结构组件相关的二进制掩码，而不是单个权重。除了剪枝单元外，其他细节与非结构化剪枝中的细节非常相似。

然而，在这些正则化方法中，\(L_{0}\)正则化是应用最广泛的技术。这些\(L_{0}\)正则化方法的主要差异在于它们选择剪枝单元的方式。Voita等人[129]将\(L_{0}\)正则化引入注意力头修剪，具体选择了一部分注意力头。McCarley等人[140]将\(L_{o}\)正则化用于修剪注意力头和FFN神经元。因式分解低秩剪枝（Factorized Low - rank Pruning，FLOP）[141]将低秩分解与\(L_{0}\)正则化相结合。这种方法涉及将矩阵\(W\)重新参数化并分解为两个较小矩阵的乘积，记为\(W = PQ\)，其中\(P_{k}\)和\(q_{k}\)分别表示\(P\)的第\(k\)列和\(Q\)的第\(k\)行。剪枝单元是\(p_{k}\)和\(q_{k}\)的组合。此外，引入了增广拉格朗日方法来调节FLOP中的稀疏率。粗粒度和细粒度剪枝（Coarse - and Fine - grained Pruning，CoFi）[142]使用\(L_{0}\)正则化联合修剪粗粒度和细粒度模块，包括Transformer模型的注意力层和FFN层、单个注意力头、FFN神经元和隐藏维度。值得注意的是，隐藏维度上的掩码在所有Transformer层中共享，并采用了增广拉格朗日方法。通过与逐层蒸馏方法相结合，CoFi在实验中实现了超过10倍的加速，同时准确率仅略有下降。

除了\(L_{0}\)正则化，\(L_{1}\)正则化也有相关研究。SIMPLE [143]将\(L_{1}\)正则化引入结构化剪枝，将注意力头、FFN的中间神经元和隐藏维度作为可压缩组件。隐藏维度上的掩码在各层之间共享，类似于CoFi [142]中采用的方法。通过基于稀疏性诱导目标学习这些可压缩组件的掩码，可以获得不同大小的剪枝模型。这些剪枝模型随后可以通过因果蒸馏目标进行微调，以提高性能。
4. 其他方法：除了基于度量的分类外，当某些结构化剪枝方法指定的剪枝单元相同时，它们表现出显著的相似性。

第一类其他结构化剪枝是层剪枝[144,145,146]。上述剪枝单元，如注意力头和神经元，规模相对较小，需要更详细的剪枝方案来确定哪些应该被修剪。相反，当处理更大的剪枝单元（如整个层）时，许多方法倾向于在确定最有效的网络配置之前，对多种剪枝方案进行直接实验。这是因为层的数量较少，测试成本较低。

除了层剪枝，还有一系列关于标记剪枝[147,148,149]的研究，这种方法不会改变底层网络架构。标记剪枝涉及在推理过程中从序列中删除不重要的标记，以减少计算需求。学习标记剪枝（Learned Token Pruning，LTP）[148]是一种简单有效的方法，用于在输入序列通过Transformer层时自适应地删除不重要的标记。每个标记的剪枝度量由Transformer块的归一化注意力概率之和确定。

除了前面提到的剪枝单元外，结构化剪枝还包括各种各样的单元。例如，谱归一化恒等先验（Spectral - Normalized Identity Prior，SNIP）[150]采用一种策略，通过将残差连接转换为严格的恒等映射来修剪注意力和FFN子层。SNIP为激活向量设置特定的阈值，低于阈值的向量会导致残差块（即注意力和FFN子层）被修剪。

 4.3 大型语言模型的剪枝方法

在上一节中，我们介绍了参数数量少于10亿的中型语言模型的剪枝方法。这些方法中的大多数在剪枝后采用全量微调来提高性能。然而，随着参数数量的增加，全量微调变得更加困难甚至不可行。这种差异凸显了专门为大型语言模型设计的剪枝技术研究领域面临的重大挑战。为了解决这个问题，一方面，某些剪枝方法选择结合参数高效调整技术来降低微调成本。另一方面，其他方法放弃微调过程，依靠优化的剪枝过程来固有地保持模型性能。这些替代方法的可行性部分归因于大型语言模型中的大量参数。参数数量越多，模型中存在冗余的可能性就越高。

在本节中，我们将介绍大型语言模型的剪枝方法，与中型语言模型剪枝方法部分的介绍顺序一致。大型语言模型的剪枝方法与中型语言模型的剪枝方法类似，但某些方法的主要区别在于省略了微调过程。为了更全面地比较这些方法，我们汇总了这些剪枝方法的特点，如表3所示。
表3：各种大型语言模型剪枝方法的总结。

 4.3.1 大型语言模型的非结构化剪枝

由于非结构化剪枝方法相比结构化剪枝方法在保持模型性能方面具有更大的能力，本节中所有针对大型语言模型的非结构化剪枝方法都采用了避免微调过程的方法，如表3所示。实验表明，这些方法可以在模型性能相对适度下降的情况下达到50%的稀疏率。

大型语言模型的两种开创性非结构化剪枝方法是SparseGPT [154]和Wanda [151]，它们成为许多后续方法进行比较的基线。随后的非结构化剪枝方法在各种NLP任务中展示了超越SparseGPT和Wanda的能力，从而获得了更优的结果。虽然非结构化剪枝方法很难实现推理加速，但它们可以很容易地与N:M稀疏性[119]相结合来加速推理速度，这在SparseGPT和Wanda中也进行了实验。

这些非结构化剪枝方法需要极少的校准数据。最少的校准数据用于模型的单次前向传递，专门用于获取激活值或梯度，以计算权重的重要性，这仍然是剪枝结果的一个影响因素[166]。

接下来，我们将按照剪枝度量的顺序介绍大型语言模型中的这些非结构化剪枝方法。在本次研究中，未发现与正则化相关的方法，因此本节将分为基于幅度的方法和基于损失的方法的介绍。
1. 基于幅度的剪枝：当直接将幅度剪枝[98]应用于大型语言模型时，即使采用参数高效的微调策略[167,168]，结果也不是很有竞争力。因此，在基于幅度的剪枝方法中，与仅使用权重幅度作为中型语言模型的剪枝度量不同，大型语言模型中更多的基于幅度的剪枝方法将权重和激活值的幅度结合作为剪枝度量。例如，Wanda [151]和RIA [152]使用权重和激活度量。除了权重和激活的幅度外，E - Sparse [153]还将信息熵引入度量中。

Wanda（基于权重和激活的剪枝）[151]引入了一种新颖的剪枝度量，同时考虑了权重和激活值的幅度。其动机是，权重的重要性不应孤立地评估，而应考虑其与相应激活值的乘积。例如，考虑一个全连接层，权重由\(W\)表示，维度为\((C_{out }, C_{in })\)。在语言模型的背景下，这个线性层接收输入激活\(x\)，维度为\((N ×L, C_{i n})\)，其中\(N\)和\(L\)分别表示批量和序列维度。对于每个权重，其重要性通过其幅度与相应输入特征范数的乘积来量化。具体而言，权重\(w_{ij}\)的得分\(S_{ij}\)定义为：
\(S_{ij}=\left|W_{ij}\right| \cdot\left\| X_{j}\right\| _{2}\) (22)
其中\(\left\|X_{j}\right\|_{2}\)评估跨\(N ×L\)个不同标记的第\(j\)个特征的\(L_{2}\)范数。值得注意的是，结果表明Wanda在显著更短的时间内实现了与SparseGPT相当的性能。

与Wanda [151]类似，RIA（相对重要性和激活）[152]也同时考虑了权重和激活。主要区别在于其缓解通道损坏（即权重矩阵的行和列被整体修剪）的方法。RIA用相对重要性代替了权重的幅度。这种相对重要性计算为单个权重的幅度除以其相应行和列的权重幅度之和。因此，通过使用相对重要性，不同行和列之间的比较变得相对公平，减轻了由其幅度变化引入的潜在偏差。RIA可以进一步与通道置换相结合，在N:M稀疏性下最大限度地保留重要权重，从而在特定硬件上实现实际的加速。
2. 基于损失的剪枝：在基于损失的方法中，观察到剪枝度量涉及权重相对于损失的一阶或二阶导数。本节中讨论的二阶方法都受到两种早期基于损失的二阶剪枝方法的启发，即最优脑损伤（OBD）[114]和最优脑外科医生（OBS）[115]。

SparseGPT [154]是一种二阶剪枝方法，将SparseGPT [154]是一种二阶剪枝方法，将OBS [115]技术应用于GPT系列模型。它是首个能在100亿及以上参数规模模型上高效工作的剪枝方法。SparseGPT的剪枝方法主要由两个部分构成：掩码选择和权重重构过程。最初，掩码选择基于一种度量（如权重幅度）来识别要剪枝的权重。随后，使用OBS方法对未剪枝的权重进行优化，以重构压缩后的模型（即更新剩余参数），从而补偿被剪枝的权重。SparseGPT的剪枝过程仅需极少的校准数据。这些数据经过一次前向传播，在此过程中，未剪枝的权重仅更新一次。该方法的结果表明，通过单次权重剪枝，大型语言模型可以被压缩到高稀疏度，且无需进行微调。重要的是，通过困惑度和零样本性能指标评估，这种压缩带来的精度损失较低。同样，LLM Surgeon [165]扩展了OBS方法，但它适用于非结构化和结构化剪枝。

基于OBS和OBD的概念，Shao等人 [155]提出了一种新的剪枝度量，称为改进的显著性准则（Improved Saliency Criterion，ISC）。ISC通过直接将源自OBS和OBD的度量相加而设计得出。这一新度量旨在为剪枝过程中评估模型参数的重要性提供全面且精细的评估。除了提出ISC，Shao等人还提出为每个矩阵单独分配稀疏率。通过这种方式，在每个权重矩阵内自适应地选择剪枝目标。

除了上述二阶方法，也有针对一阶方法的相关研究 [156,157]。基于梯度的语言模型剪枝器（Gradient-based Language Model Pruner，GBLM-Pruner）[156]是一种一阶剪枝方法。权重的重要性由其幅度与不同样本上相应梯度的归一化乘积定义，这可以看作是传统一阶方法（即梯度 - 权重乘积）的扩展。此外，特征激活也可以集成到剪枝度量中以提升性能。

 4.3.2 大型语言模型的结构化剪枝

与非结构化剪枝不同，结构化剪枝不受硬件限制，在剪枝后能够在常规硬件上实现推理加速。然而，由于网络结构的改变，这些方法可能比非结构化剪枝导致更多的性能下降，因此需要一个微调过程来恢复性能。所以，虽然在大型语言模型的非结构化剪枝中放弃了微调，但在结构化剪枝中，微调被广泛应用，不过是以参数高效的方式进行。与非结构化剪枝类似，大型语言模型的结构化剪枝也有其开创性方法，LLM-Pruner [160]，它作为后续方法的基线，便于进行有意义的比较。

我们将在以下部分讨论这些针对大型语言模型的结构化剪枝方法。同样，我们将按照剪枝度量的顺序介绍这些方法，包括基于幅度的剪枝、基于损失的剪枝和正则化。

1. 基于幅度的剪枝：大型语言模型的基于幅度的剪枝方法将行或列视为剪枝单元 [158,159,169]。例如，基于波动的自适应结构化剪枝（Fluctuation-based Adaptive Structured Pruning，FLAP）[158]的剪枝单元是列。权重矩阵每列的重要性得分通过 “波动度量” 来衡量。该度量是每个输入特征的样本方差，并用相应列的权重矩阵的平方范数进行加权。此外，为了避免对微调的需求，FLAP引入了偏差补偿机制，旨在减轻因组件移除而产生的不利影响。

2. 基于损失的剪枝：在应用于大型语言模型的基于损失的结构化剪枝方法中，梯度仍然是关键信息，这与在中型模型中的重要性类似。以下方法以不同方式利用梯度信息 [160,161,162,170]，例如定义剪枝结构、选择剪枝目标等。这些方法与传统方法最显著的区别在于它们避免了预定义的剪枝单元（如注意力头、神经元）。相反，其中一些方法动态地识别和指定剪枝单元。

例如，LLM-Pruner [160]在剪枝过程中移除非关键的耦合结构。这些耦合结构通过定义结构依赖性（即神经元之间的连接依赖关系）自动识别和提取。一个耦合结构由一组权重组成。单个权重的重要性通过损失的变化来表示，使用泰勒展开扩展到二阶。二阶项中的海森矩阵的对角线通过一阶信息用费舍尔信息矩阵近似。最终，通过求和、乘积或其他方法对一组权重的重要性进行聚合，以确定该组的整体重要性。在评估每组的重要性之后，根据预定义的剪枝率修剪重要性较低的组。LLM-Pruner中的微调过程应用了一些参数高效的调整技术，如LoRA。这使得使用少量数据就能对剪枝后的模型进行快速有效的微调。实验结果表明，当移除20%的参数时，剪枝后的模型能够保持大部分原始模型的性能。然而，更激进的剪枝策略（如移除50%的参数）会导致模型性能大幅下降。这一观察结果也凸显了通过结构化剪枝在保持模型性能的同时实现高稀疏率的难度。

与LLM-Pruner类似，LoRAShear [161]在依赖图中发现最小的移除结构。然而，LoRAShear专门在LoRA模块上构建依赖图，考虑到它们的可学习性。然后利用知识分布分析来识别关键结构，并将其标记为不可剪枝。LoRAShear的一个独特之处是引入了LoRA半空间投影梯度（LoRA Half-Space Projected Gradient，LHSPG）用于渐进式结构化剪枝。LHSPG利用LoRA模块的信息来识别和移除冗余结构，同时保留重要结构中存储的知识。这是通过将冗余结构投影到零，将知识转移到关键结构来实现的。

与手动设计剪枝特征不同，Ji等人 [170]提出了一种新颖的方法，即使用非神经模型（具体为梯度提升决策树，Gradient Boosting Decision Tree，GBDT）作为精度预测器。使用这种精度预测器能够进一步优化搜索空间和搜索过程，以自动识别最优的剪枝模型。通过将GBDT训练为精度预测器，模型获得了评估和预测不同剪枝配置对神经网络精度影响的能力，从而有助于更高效、自动化地选择最优的剪枝模型。

3. 正则化：在应用于大型语言模型的正则化方法中，当代方法主要遵循为早期中型语言模型建立的原则，并融入了一些通用的改进和优化。

Sheared LLaMA [163]可以看作是CoFi [142]的扩展。这种方法使用\(L_{0}\)正则化对基于Transformer的模型中的粗粒度和细粒度模块进行联合剪枝。被剪枝的模块包括层、单个注意力头、FFN神经元和隐藏维度，与CoFi中的情况相同。Sheared LLaMA引入了两个新颖且重要的组件。第一个组件是目标结构化剪枝，它将剪枝构建为一个约束优化问题。这种公式化旨在学习剪枝掩码，以搜索与预先指定的目标架构匹配的子网络，同时最大化性能。第二个组件是动态批量加载，这是一种根据每个域的损失减少率按比例加载训练数据的策略。这种方法有效地利用了数据，并在训练过程中加速了整体性能的提升。在全资源设置下，Sheared LLaMA获得的紧凑模型优于从头开始训练的同等大小的模型。

Compresso [164]将LoRA集成到\(L_{0}\)正则化中。\(L_{o}\)正则化用于优化覆盖包括头、FFN中间神经元和隐藏维度等模块的二进制掩码。同时，在指令调整过程中通过LoRA更新模型参数。Compresso的一个创新之处是引入了协作剪枝范式，其中剪枝算法和目标大型语言模型通过协作prompt共同学习，在指令调整过程中确定最优的剪枝决策。prompt解释了剪枝的概念和目的，告知大型语言模型它正在接受剪枝，并鼓励大型语言模型更好地适应剪枝过程。通过纳入这个信息丰富的prompt，Compresso旨在增强大型语言模型在剪枝过程中的理解和协作，有助于提高性能并适应修改后的模型结构。

 4.4 大型语言模型剪枝的其他主题

 4.4.1 提高大型语言模型剪枝的效果

已经开发了几种辅助技术来提高针对大型语言模型的剪枝方法的效果，包括为子区域定制的稀疏率 [171,172]、剪枝后微调方法 [89,167,173,174,175] 以及硬件优化 [176,177]。虽然这些技术不属于新的剪枝方法，但它们可以很容易地与现有的大型语言模型剪枝方法集成，以提高整体剪枝效果。

一种定制稀疏率的方法是异常值加权层稀疏性（Outlier Weighed Layerwise sparsity，OWL）[171]。OWL中的实验表明，合适的层稀疏率与异常值的出现密切相关。因此，OWL的稀疏率与每层中观察到的异常值比率成正比。与普遍在所有层上应用统一稀疏率的大型语言模型剪枝策略不同，OWL引入了一组定制的非均匀层稀疏率。另一种剪枝后微调方法是动态稀疏无训练（Dynamic Sparse No Training）[174]，它为稀疏大型语言模型引入了一种无需训练的微调方法。这允许对稀疏大型语言模型进行轻微更新，实现进一步的优化，而无需完整的微调过程。在没有昂贵的反向传播的情况下，动态稀疏无训练以在稀疏大型语言模型上执行迭代权重剪枝和增长的方式，最小化密集和稀疏大型语言模型之间的重构误差。

实验结果表明，这些技术可以显著提高现有剪枝方法（如Wanda和SparseGPT）的性能。这些发现表明，可以通过与剪枝方法核心无关的多种方式来提升剪枝的性能。

 4.4.2 大型语言模型剪枝的未来工作

虽然大型语言模型剪枝领域已经取得了丰硕的成果，但它仍然面临着重大挑战。有两个主要问题尤为关键。

首先，将剪枝与其他方法（如量化 [154] 和知识蒸馏 [163]）相结合对于实现有竞争力的性能至关重要。与过去视觉模型领域的剪枝成果相比，当前大型语言模型剪枝的成果相对不那么令人满意。因此，一个关键挑战是增强剪枝方法本身的有效性，确保即使单独使用时，它也能表现出色。

其次，微调成本是大型语言模型剪枝中的一个重大挑战。许多大型语言模型的剪枝方法采用一次性剪枝而不进行微调，以最小化计算负担。或者，一些方法结合参数高效调整技术来降低训练成本。然而，这些策略不可避免地会牺牲剪枝后模型的性能。该领域的研究人员和从业者必须继续应对无法进行全量微调的挑战，特别是在处理旨在提高剪枝性能的大型语言模型时。

总之，应对这些挑战对于推进剪枝技术的有效性和实用性至关重要。

 5 知识蒸馏

知识蒸馏（KD）是一种常用的模型压缩和加速技术。其具体实现过程是将复杂教师模型学到的知识转移到更简单的学生模型中，从而使学生模型能够更简洁高效地表达教师模型的知识。

在5.1节中，我们将介绍知识蒸馏的一些基本概念，并对知识蒸馏方法进行简要分类。然后在5.2节中，我们将总结各种针对中型语言模型（参数约为10亿的语言模型）的知识蒸馏方法，并根据蒸馏是发生在预训练阶段、微调阶段还是两者都有，将它们分为三组。最后在5.3节中，我们将详细概述针对大型语言模型（参数超过10亿的语言模型）的知识蒸馏方法，将其分为黑盒蒸馏和白盒蒸馏两类。

 5.1 基本概念

理解知识蒸馏的核心需要回答三个问题：什么是知识、知识在谁之间传递以及如何传递知识。简单来说，知识可以概括为模型所具备的能力（分类、推理等）。在蒸馏过程中，知识的来源是教师模型，知识的接收者是学生模型。也就是说，一个训练良好的教师模型至关重要，我们的目标是让学生模型获得或强化教师模型所具备的能力。然而，关键在于知识如何传递。知识蒸馏的先驱Hilton等人 [178] 首次使用教师模型和学生模型的softmax层的输出进行知识传递。他们设计了以下损失函数来训练学生模型，从而实现知识的转移：
\(L=\alpha \cdot L_{D}\left(p\left(z_{t}, T\right), p\left(z_{s}, T\right)\right)+(1-\alpha) \cdot L_{S}\left(y, p\left(z_{s}, T\right)\right)\) (23)
其中\(L_{D}(p(z_{t}, T), p(z_{s}, T))\)表示学生模型和教师模型softmax层输出的差异，\(L_{S}(y, p(z_{s}, T))\)表示学生模型softmax层输出与真实标签之间的差异。这两个差异都使用交叉熵损失。\(\alpha\)表示权重系数，\(p_{i}\)的具体表达式如下：
\(p_{i}=\frac{\exp \left(z_{i} / T\right)}{\sum_{j} \exp \left(z_{j} / T\right)}\)
其中\(T\)用于放大错误标签对知识传递的影响，从而使学生模型能够从单个样本中获取更多知识。

随后的研究人员采用了多种方法来实现知识转移，主要分为以下四类：基于logit的KD、基于特征的KD、基于关系的KD和黑盒KD。在图5中，我们还简要概述了这些蒸馏方法及其关系。

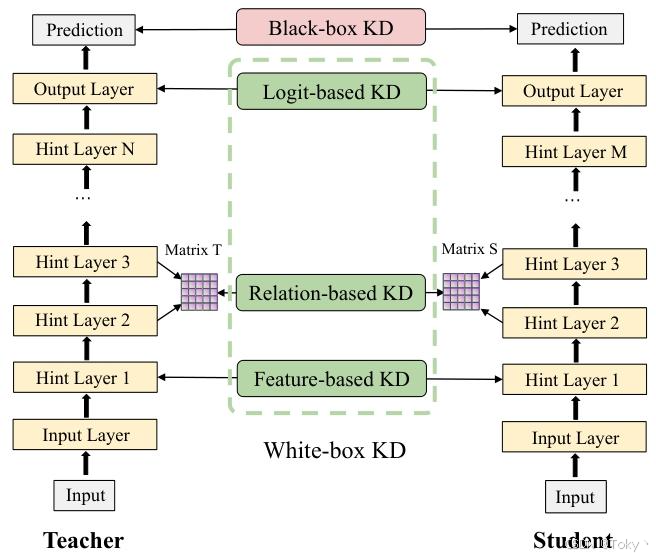
图5：知识蒸馏的分类

1. 基于logit的KD：顾名思义，基于logit的KD是一种使用教师模型的logits进行知识转移的蒸馏范式。我们可以写出基于logit的知识蒸馏损失函数的一般形式：
\(L_{logit }=\mathcal{L}\left(p\left(z_{t}\right), p\left(z_{s}\right)\right)\)
其中\(\mathcal{L}(\cdot)\)表示交叉熵损失 [178]、Kullback - Leibler散度（KLD）损失 [179] 等。

显然，Hilton等人的方法是基于logit的知识蒸馏的一个例子。
2. 基于特征的KD：由于基于logit的知识蒸馏中，学生模型获取的知识有限，研究人员旨在更好地模仿教师模型的行为。因此，他们引入了基于特征的知识蒸馏。具体来说，这涉及匹配学生模型和教师模型中间层的输出，要求学生模型不仅要知道结果，还要理解其背后的过程。基于特征的知识蒸馏损失函数的一般形式如下：
\(L_{feature }=\mathcal{L}\left(\left(f_{t}(x), r\left(f_{s}(x)\right)\right)\right.\)
其中\(f_{t}(\cdot)\)和\(f_{s}(\cdot)\)分别表示教师模型和学生模型的特征图。\(\mathcal{L}(\cdot)\)是用于拟合特征的函数，\(r(\cdot)\)用于使教师模型和学生模型的特征图具有相同的形状。

例如，FitNet [180] 利用教师模型和学生模型中间层的特征图来调整学生模型的参数。它还使用均方误差（MSE）以及一个可学习的矩阵作为\(\mathcal{L}(\cdot)\)和\(r(\cdot)\)。
3. 基于关系的KD：此外，研究人员希望学生模型学习教师模型如何处理不同数据之间的关系，从而提出了基于关系的知识蒸馏。这种关系主要体现在两个方面：同一样本不同层输出之间的关系以及不同样本输出之间的关系。其损失函数的一般形式如下：
\(L_{response }=\mathcal{L}\left(\left(f_{t}\left(t_{i}, t_{j}\right), f_{s}\left(s_{i}, s_{j}\right)\right) \quad(27)\right.\)
其中\(t_{i}\)，\(t_{j}\)和\(s_{i}\)，\(s_{j}\)是来自教师模型和学生模型的特征表示。它们可以表示不同层的输出或不同样本的输出。\(f_{t}(\cdot)\)和\(f_{s}(\cdot)\)表示相似性函数。

例如，FSP [181] 使用相同大小的特征图作为特征表示，并采用Gram矩阵和MSE作为\(f(\cdot)\)和\(\mathcal{L}(\cdot)\)。
4. 黑盒KD：上述三种蒸馏方法都基于教师模型的内部信息可访问这一前提，因此它们都属于白盒蒸馏（在训练过程中需要访问教师模型内部数据的蒸馏方法）。然而，许多当代的闭源大型模型的内部信息无法访问，我们只能获得模型的预测结果。通过教师模型的预测结果进行知识传递的蒸馏模式被称为黑盒知识蒸馏。

 5.2 中型语言模型的知识蒸馏

随着Transformer架构的出现，各种基于Transformer结构的中型语言模型（如BERT、GPT - 2等）被提出。这些语言模型通过预训练和微调两个训练过程进行训练。具体来说，在预训练阶段，我们在大规模无标签数据集上训练模型，以学习语言的一般特征和结构。随后，在微调过程中，我们在有标签数据上进一步训练模型，使其适应给定任务的特定特征和要求。因此，与以往的蒸馏方法不同，这些模型的蒸馏分为两类：微调蒸馏和预训练蒸馏。学生模型可以在预训练期间接收来自预训练教师模型的知识，或者在微调期间接收来自针对特定任务微调的教师模型的知识。我们将分别介绍这两种蒸馏范式。此外，我们创建了表4来说明以下提到的各种中型模型蒸馏方法的训练阶段、知识来源和损失函数。
表4：各种针对BERT的知识蒸馏方法总结。Embed.、Attn.、Hidden.和Pred.分别表示知识来自嵌入层、注意力层、隐藏层和模型的预测。

 5.2.1 微调蒸馏

微调蒸馏主要旨在为特定任务压缩模型。一般来说，微调蒸馏中的教师模型是针对特定任务进行微调后的模型。例如，Distilled BiLSTM [182]是最早在BERT上应用知识蒸馏的方法。它通过学习logits将微调后的BERT的知识转移到BiLSTM中。因此，这是基于logit的知识蒸馏在中型模型上的成功应用。随后，许多基于特征的知识蒸馏方法 [183,184]也在中型模型上得以实现。它们在嵌入层、Transformer层和预测层进行知识蒸馏，使学生模型能够从多个方面学习教师模型所掌握的知识。例如，PKD [183]引入了隐藏状态损失。它从教师模型和学生模型的中间Transformer块中选择一部分输出进行蒸馏。此外，它设计了两种对齐模式，即PKD-Skip（学生模型从教师模型的每k层学习）和PKD-Last（学生模型从教师模型的最后k层学习），实验证明前者更具优势。DynaBERT [184]也考虑了模型的宽度，融入了剪枝的思想。具体而言，它设置了一个参数——宽度乘数\(m_{w} \in(0,1)\) ，并在Transformer的多头注意力（MHA）层中保留最重要的\(m_{w}\)个注意力头，在前馈网络（FFN）中保留最重要的\(m_{w}\)个神经元，以此来初始化学生模型\(DynaBERT _{w}\) 。然后，它通过嵌入层、隐藏状态和预测层将知识从教师模型转移到宽度自适应的\(DynaBERT _{w}\) 。接着，它使用深度乘数\(m_{d}\)（类似于PKD-Skip）从\(DynaBERT _{w}\)中均匀选择Transformer层来初始化学生模型DynaBERT。之后，使用与宽度自适应过程相同的知识源，将知识从\(DynaBERT _{w}\)转移到宽度和深度自适应的DynaBERT中。Metadistil [185]指出了一般蒸馏中的两个常见问题：教师模型无法感知学生模型的能力，以及强大的教师模型不一定能有效地教导优秀的学生。为了解决这些问题，它提出了一种新颖的蒸馏方法：首先在训练数据上蒸馏学生模型S的副本S’，然后使用更新后的S’在测试数据上更新教师模型，使其学会教学。最后，使用更新后的教师模型在训练数据上蒸馏S。AD-KD [186]关注每个标记对预测结果的重要性。它旨在让学生模型理解教师模型在生成预测时优先考虑哪些标记，从而学习教师模型推理背后的原理。

上述一些方法 [183,184]从操作可行性的角度来看可以应用于预训练蒸馏，但Turc等人 [197]证明简单的预训练蒸馏方法会导致显著的蒸馏损失。因此，使用这些方法蒸馏得到的学生模型的有效性可能并不理想。此外，一些方法 [185,186]尚未在预训练蒸馏中得到应用，它们在预训练蒸馏中的适用性仍有待探索。

考虑到微调蒸馏是针对特定任务的，许多其他方法还利用了特定的知识源，使学生模型能够更有效地从教师模型获取特定任务所需的知识。因此，这些方法无法应用于预训练蒸馏。

例如，AdaBERT [187]采用搜索空间来实现学生模型结构的自适应变化。具体来说，搜索空间由多个层组成，每层包含输入节点、输出节点和隐藏的内部节点，这些节点形成一个有向图。图中的边代表从一系列基于CNN的轻量级操作中选择的候选操作。考虑到学生模型的大小和效率，AdaBERT不仅在蒸馏中使用了软目标和硬目标，还在损失函数中纳入了学生模型的归一化参数大小和浮点运算次数。最终，这个损失函数用于选择合适的基于CNN的操作。然而，MixKD [188]从数据集入手，将MixUp [198]应用于知识蒸馏，以解决训练样本有限导致学生模型知识获取不足的问题。它使用零填充使所有句子长度相同，然后对两个训练样本的词嵌入和标签进行插值，得到增强样本。然后，它将MixUp样本的损失纳入损失函数。Meta-KD [189]认识到当学生模型在一个领域学习时，可能会从其他领域的辅助知识中受益。例如，一个物理专业的学生在一位精通物理和数学的教师的指导下，可能更容易掌握物理方程。因此，为特定领域的学生模型训练一个 “通用教师” 模型变得至关重要。更准确地说，它为每个实例使用最后一个隐藏层的输出来构建一个可学习的子网络。这个子网络能够区分每个实例的领域，使知识具有可转移性，不受领域限制。在蒸馏过程中，教师模型不仅要传递输入嵌入、隐藏状态、注意力矩阵和输出logits中包含的知识，还要传递这种可转移的知识。ReAugKD [190]考虑了推理阶段。它使用来自教师模型相关任务特定知识的外部记忆来增强学生模型的有效容量。在蒸馏阶段，它在教师模型的编码器顶部添加一个经过下游任务微调的线性投影头，以生成教师嵌入，并从最后一个Transformer中获取学生嵌入。然后，它使用关系KD损失进行训练，该损失最小化教师 - 教师和教师 - 学生嵌入分布之间的差异。他们发现这种蒸馏方法可以有效地增强学生模型检索外部信息的能力。在推理阶段，它使用教师模型的软标签和预测构建一个知识库。然后，它处理知识库中与学生嵌入最相似的前k个数据条目。最终的预测通过对学生模型的预测和这些处理后的知识库条目进行加权组合得到。

此外，Enhanced KD [199]通过泰勒级数展开提出了一种新的蒸馏损失函数，即使教师模型没有针对特定任务进行微调，也能实现有效的蒸馏。这种方法降低了大量的训练成本，并且与模型架构无关。

 5.2.2 预训练蒸馏

预训练蒸馏的主要目标是获得一个参数更少且具有良好泛化能力的预训练模型。因此，其中一些方法 [191,193,194]利用了BERT训练过程中使用的损失函数。DistilBERT [191]是第一个将预训练蒸馏引入BERT的方法。它将PKD-Skip [183]（学生模型从教师模型的每k层学习）的思想应用于预训练蒸馏，并采用余弦相似性损失函数来促进隐藏状态之间的知识转移。MiniLM [192]将蒸馏的重点放在最后一个Transformer层。它利用该层的自注意力分布和自注意力值关系（值矩阵与自身的点积）来获取知识并进行蒸馏。这种方法巧妙地使学生模型具有更灵活的层数和隐藏维度。因此，它可以直接将教师模型蒸馏为一个隐藏维度较小的教师助手 [200]，然后再将教师助手蒸馏为层数更少的学生模型，从而提高学生模型的性能。MobileBERT [193]和HomoBERT [194]与DynaBERT [184]一样注重模型宽度，但它们只改变模型的宽度而保留深度，因为Turc等人 [197]证明深度对模型性能的影响更为显著。MobileBERT在教师模型和学生模型中都添加了瓶颈层和倒置瓶颈层来改变隐藏维度。然而，这种方法在实际实现中可能会破坏多头注意力（MHA）和前馈网络（FFN）之间的参数平衡。因此，作者采用堆叠FFN的方法来解决这个问题。然后，它通过Transformer层的注意力和隐藏状态进行知识蒸馏。HomoBERT与DynaBERT一样利用了剪枝的概念。但它使用教师模型初始化学生模型，以便与教师模型保持较小的差异。然后，它以输入嵌入、隐藏状态、注意力矩阵和输出logits为剪枝目标，推导出蒸馏损失函数。在每次迭代中，它根据重要性分数从学生模型中移除最不重要的神经元，并使用蒸馏损失指导学生模型的训练。这个过程在整个训练过程中迭代进行，直到学生模型达到目标大小。TinyBERT [195]结合了预训练蒸馏和微调蒸馏，使TinyBERT能够捕捉BERT中的通用领域知识和特定任务知识。它还从Transformer层的嵌入层、隐藏状态和注意力矩阵以及预测层蒸馏各种知识。但消融研究表明，微调蒸馏的影响比预训练蒸馏更为显著。TED [196]为每一层配备了一个任务感知滤波器（一个带有特定任务头的神经网络），以从该层的隐藏表示中提取知识。它在预训练和微调场景中都取得了有前景的结果。

 5.2.3 讨论

微调蒸馏的计算成本较高，因为每次切换到新任务时都需要训练一个特定任务的教师模型。因此，许多微调知识蒸馏方法 [189,190,199]被提出以降低微调过程的计算成本。但在预训练蒸馏中，学生模型是从在开放域数据上预训练的教师模型中蒸馏得到的，可以在各种下游任务上进行高效微调，这在一定程度上降低了针对多个特定任务进行蒸馏的计算成本。然而，预训练蒸馏也带来了许多新的挑战。例如，教师模型比学生模型具有更大的容量和更强的表示能力，学生模型在大量开放域训练数据上很难产生与教师模型匹配的预测。因此，对于一般方法而言，在预训练蒸馏和微调蒸馏之间的选择取决于我们在模型大小和性能之间所做的权衡。

 5.3 大型语言模型的知识蒸馏

最近，越来越多的大型语言模型（LLMs）被开发出来。然而，许多这些大型模型是闭源的，这对这类模型的知识蒸馏施加了显著限制。虽然学生模型无法从内部信息中获取知识，但我们仍然可以利用教师模型的响应（这是剩余的知识来源）将信息转移到学生模型中。根据学生模型的知识来源是否仅为教师模型提供的答案，大型语言模型的蒸馏可以分为黑盒蒸馏和白盒蒸馏。

 5.3.1 黑盒蒸馏

尽管传统的蒸馏方法可能不再适用，但大型语言模型的一些独特属性为我们提供了突破的机会。研究人员发现，当模型的参数足够大时，它们会展现出惊人的涌现能力，使其能够处理复杂的任务。许多黑盒蒸馏方法利用了这些能力，通常有三种常用方法：指令跟随、思维链（Chain-of-Thought，CoT）和上下文学习。

1. 指令跟随：指令跟随能力是指大型语言模型能够根据特定指令（指示模型要完成的任务）和输入（完成该指令所需的数据）生成相应的输出。由于黑盒蒸馏只能通过数据集传递知识，因此需要一个足够全面的数据集。因此，这种方法 [201,202,203,204]的常见做法是构建一个大型数据集（包含指令、输入和输出），使学生模型能够尽可能多地从教师模型中学习。

具体来说，SELF-INSTRUCT [201]采用自蒸馏方法，模型同时作为教师模型和学生模型。它首先获取一个手动策划的小规模任务池，每个任务由一个指令和相应的输入 - 输出对组成。随后，它从任务池中选择一部分指令作为上下文示例，让模型生成新的指令以及匹配的输入和输出。最后，它过滤掉冗余过多或语言模型无法处理的内容，将合格的数据放回任务池。这个迭代过程不断生成一个广泛的数据集，用于微调学生模型。这已成为指令跟随蒸馏的一种范式，130亿参数的开源模型Alpaca [205]、Vicuna [206]和GPT4All [207]就是基于这种范式进行了一些调整后训练得到的。同样基于这个思路，LLaMA-GPT4 [202]和LaMiniLM [203]构建了各自的指令集并微调较小的模型。与SELF-INSTRUCT相比，它们的突破之处在于：LLaMA-GPT4使用GPT-4生成了一个包含52000个英语和中文指令跟随数据集，并微调了两个学生模型LLaMA-GPT4和LLaMA-GPT4-CN。

此外，它还训练了一个专门用于评估模型响应质量的奖励模型。LaMni-LM丰富了用于生成指令的模型类型和指令主题，构建了一个包含258万个样本的大规模数据集，用于微调较小参数的学生模型，并取得了良好的效果。然而，在上述方法中，学生模型并未参与数据集的选择，因此在数据集生成过程中教师模型无法及时从学生模型获得反馈。针对这个问题，Lion [204]采用了对抗知识蒸馏，学生模型不仅从教师模型的响应中学习，还由一个裁判进行评估，以评估其与教师模型的差异。这有助于识别学生模型表现不足的 “困难” 指令，从而生成新的 “困难” 指令，使教师模型在学习过程中能够获得反馈。PERsD [208]使用单元测试用例评估学生模型的尝试并获得执行反馈。然后，它促使教师模型改进学生模型的尝试，以便学生模型可以在个性化数据上进行训练。

一些工作专注于特定任务的指令跟随蒸馏。例如，UniversalNER [209]对命名实体识别（NER）任务进行了深入研究。因此，与上述增加指令多样性的方法不同，它的重点在于增强输入的多样性，以提高模型在多个领域的泛化能力。具体来说，它直接从跨多个领域的大型语料库中采样输入，然后使用大型语言模型生成输出。在获得数据后，它使用对话式调优格式训练学生模型，使其能够识别输入文本中包含的每种实体类型的实体。

此外，使用大型语言模型构建强化数据集来微调学生模型的这种方法并不局限于指令跟随，而是黑盒蒸馏的一种常见方法。

2. 思维链：思维链能力是指大型语言模型能够根据给定prompt中的推理依据，对问题提供更好的答案。思维链蒸馏的典型范式 [210,211,212,213]是利用大型模型生成包含推理依据的强化数据集，然后用于微调学生模型。因此，关注的问题围绕如何生成高质量的用于训练的推理依据 [210,214,215,216,217,218,219,220,221,222,223]，以及如何确保学生模型有效地利用这些推理依据 [210,212,215,216,217,223,224]。Li等人 [210]系统地探索了从大型语言模型生成解释的三种方法和三种带解释的多任务学习方法。最终发现CROP（带有合理化prompt备份的思维链，Chain of Thought with Rationalization Prompting backup）和MT-CoT（带思维链的多任务学习，Multi-task Learning with Chain of Thought）是出色的方法。具体来说，CROP是指对于一个包含问题和答案的数据集，教师模型首先根据问题生成一个解释和答案。如果答案正确，则保留解释。如果答案错误，则教师模型根据问题和正确答案生成一个解释。最终，得到一个包含问题、解释和答案的数据集，用于微调学生模型。MT-CoT是指学生模型的训练过程有两个任务。模型不仅需要学习预测答案，还需要提供解释。此外，在提供解释的任务中，模型需要通过推理步骤得出正确答案。此外，Distilling Step-by-Step [212]证明，即使原始数据集仅包含问题而没有答案，也能取得良好的效果。Fine-tune-CoT [214]应用现有的零样本思维链prompt方法，从大型教师模型生成推理依据，并用于微调较小的学生模型。它还提出了多样化推理来扩充学生模型的训练数据，以使学生模型具有更好的性能。此外，SCoTD [220]和MCC-KDc [221]也对推理依据的多样性进行了深入探索。Fu等人 [225]发现通过思维链蒸馏确实可以将学生模型的能力从一般任务转移到特定任务。SOCRATIC CoT [215]将一个问题分解为几个子问题，以指导推理依据的生成。它首先从数据集中选择一部分数据，手动分解问题并为每个子问题提供答案。这些作为示例提供给大型语言模型，以生成其余数据的子问题和答案。然后，根据最终结果的正确性对得到的数据集进行筛选强化。最后，使用这个数据集训练两个学生模型，一个用于提问，一个用于回答问题。SCOTT [216]考虑了思维链中的两个问题。首先，教师模型生成的推理依据可能与答案不匹配或没有意义。其次，学生模型在学习过程中可能难以将推理依据与答案联系起来。为了解决这些挑战，SCOTT在推理依据生成过程中采用对比解码，使模型更加关注答案。这要求教师模型的解码过程是可调节的。在学生模型的训练过程中，SCOTT引入反事实推理依据，以指导学生模型获得不同的答案，从而在推理依据和答案之间建立更紧密的关系。KARD [217]通过从外部知识库检索信息来解决小模型内存能力有限的问题。Program Distillation [218]和PaD [219]都利用程序作为推理依据，并在数学应用题上取得了有前景的结果。DOCTOR [222]利用教师模型生成包含常识知识的问答式推理依据，然后筛选并选择高质量的多跳推理用于训练学生模型。Wang等人 [223]构建了一个交互式多轮学习范式，学生模型首先向教师大型语言模型提供其学习状态，然后教师模型可以提供定制的推理依据作为反馈。他们还通过促使较小的语言模型对错误进行自我反思，挖掘其推理潜力。

3. 上下文学习：上下文学习（ICL）也是大型模型涌现能力的一种体现，指的是大型模型能够根据一些输入 - 标签示例，在不更新后的模型参数的情况下，为新输入生成正确输出的能力。基于此，上下文学习蒸馏（In - context Learning Distillation）[226]利用两种少样本学习范式，即元上下文调整（Meta In - context Tuning，Meta - ICT）和多任务上下文调整（Multitask In - context Tuning，Multitask - ICT），通过蒸馏将教师模型的上下文学习能力转移到学生模型中。在Meta - ICT中，它使学生模型能够通过上下文学习和教师的帮助适应未见任务。但在Multitask - ICT中，它将所有目标任务视为训练任务，并在上下文学习蒸馏中直接使用来自目标任务的示例。结果表明，多任务上下文调整更为有效，尽管其计算成本更高。LLM - R [227]首先基于大型语言模型的反馈训练一个奖励模型，以评估候选示例的质量，随后通过知识蒸馏训练一个检索器，该检索器能够为大型语言模型识别高质量的上下文示例。
4. 其他方法：除了上述三种范式，还有其他方法通过生成特定的强化数据集，使学生模型获得特定能力。例如，符号知识蒸馏（Symbolic Knowledge Distillation）[228]利用大型语言模型收集数据并进行筛选，从而获得高质量的常识知识图谱，用于训练常识模型。DISCO [229]使用大型语言模型获取反事实数据，并利用一个大型教师自然语言推理（NLI）模型进行筛选，进而获得高质量的数据集，以提升学生模型在自然语言推理任务中的能力。PubMedBERT [230]对不良药物事件（ADE）提取进行了案例研究，并提出了一种新颖的框架，该框架同时处理不良事件（AE）实体提取和ADE关系提取，以降低计算需求。Promptmix [231]利用大型语言模型按比例混合和重新标记文本数据以解决分类问题，旨在获得更强的数据集用于训练。然而，Gudibande [232]证明，不断增加模仿训练数据可能会导致模型单纯模仿而缺乏理解，因此增强基础模型的能力也是黑盒蒸馏中不可或缺的一部分。

 5.3.2 白盒蒸馏

与黑盒蒸馏相比，白盒蒸馏的相关工作相对较少，但仍有一些探索。例如，MINILLM [233]和GKD [234]都聚焦于损失函数，他们发现在语言生成任务中，当学生模型的分布不足以覆盖教师模型分布的所有模式时，前向KL散度会高估教师分布的空白区域。而反向KL散度则关注主要模式，使学生能够学习教师分布的主要部分。此外，它并不强制学生模型与教师模型的分布完全匹配，而是旨在利用教师提供的信息辅助学生模型的训练。因此，MINILLM从学生分布中采样，并使用策略梯度定理计算反向KL散度。由于策略梯度存在高方差和奖励作弊的问题，MINILLM提出了单步正则化、教师混合采样和长度归一化来解决这些问题。与MINILLM类似，GKD利用反向KLD和Jensen - Shannon散度（JSD）来增强学生模型的表达能力。但它使用策略内知识蒸馏（on - policy KD）来缓解训练和评估之间的分布不匹配问题，这涉及从学生分布中采样而无需通过学生模型的采样过程进行反向传播，而MINILLM需要进行反向传播。事实证明，这种梯度处理方法相对简单但有效。Padmanabhan等人 [235]通过促使语言模型从实体定义生成延续内容来生成一个转移集，然后更新模型参数，使学生模型的分布与教师模型在转移集上的分布相匹配。TSLD [236]利用logit蒸馏来重构中间表示，并应用标记级logit缩放，减少了将量化感知训练（QAT）应用于生成式语言模型时引入的误差。MiniMA [237]发现当学生模型的参数约为教师模型参数的40%时，蒸馏效果最佳。它利用LLaMA2 - 7B进行结构化剪枝和基于logit的知识蒸馏，以训练一个30亿参数的MiniMA模型。

由于大型语言模型的闭源性质带来的限制，白盒蒸馏面临一定的约束。然而，随着越来越多样化的开源大型语言模型（如Alpaca、Vicuna）的出现，白盒蒸馏在未来具有巨大的潜力。

 6 紧凑架构设计

紧凑架构设计是一种追求效率和精简的理念，旨在通过优化网络结构和算法，在减少计算资源消耗和内存使用的同时，显著提高模型效率。具体而言，它可以分为微观和宏观两个层面的研究。本节将重点关注注意力计算的优化和Transformer架构设计。由于Transformer层目前是大型语言模型的主要组成部分，且对大型和中型模型而言并无差异，因此我们在此处不会根据模型大小对方法进行具体分类。

 6.1 高效注意力机制

Transformer的标准自注意力机制对于长度为N的序列，其时间和空间复杂度为\(O(N^{2})\) ，这极大地限制了它在各个领域的进一步扩展，并使其难以处理长序列问题。为了解决这个问题，出现了许多改进注意力机制的工作，其中许多工作致力于提高计算和内存效率。我们将这些工作称为高效注意力机制。根据出发点和方法特点，我们将这些工作分为三类：稀疏注意力、线性近似注意力和FlashAttention。也有一些独特的工作，如Transformer - XL [238]，它没有在注意力算子内进行改进，因此这里将不讨论。

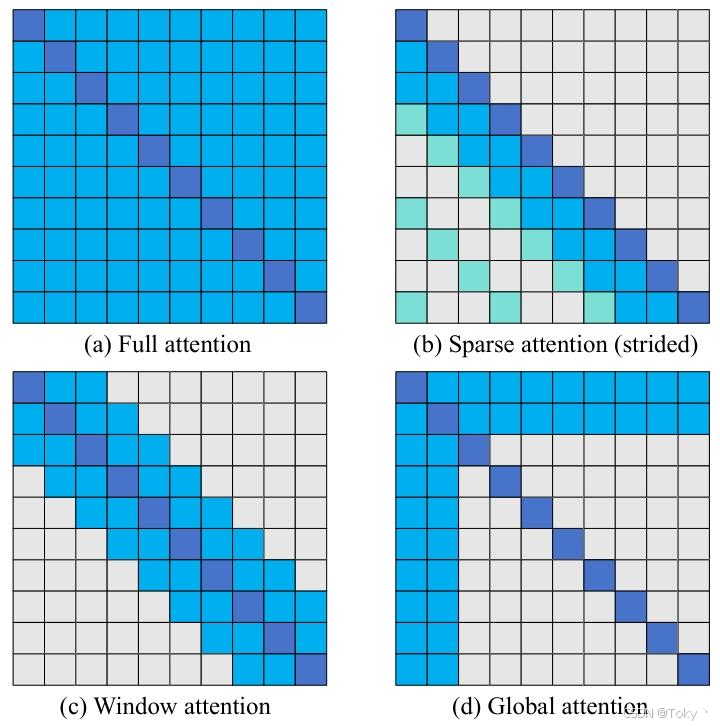
图6：比较稀疏注意力模式。(a) 全自注意力；(b) 步长式注意力；(c) 窗口注意力；(d) 全局注意力

1. 稀疏注意力：稀疏注意力方法 [239,240,241,242,243,244,245,246,247,248,249,250]允许每个标记仅关注局部或主要相关的项目，以实现稀疏注意力模式，从而降低计算和内存复杂度。根据这些方法的特点，我们将它们分为基于步长的方法、基于窗口的方法和基于数据的方法。
    基于步长的方法：基于步长的方法 [239,240,241]通过让每个标记关注长度为步长的几个前序标记来实现稀疏注意力模式，从而降低计算复杂度。[239]是一项早期工作，它提供了两种分解注意力的方式：步长式（图6 (b)）和固定注意力模式。这些方式允许每个查询仅关注预设位置，将自注意力的复杂度降低到\(O(N \sqrt{N})\) 。然而，这种方法的适用性有限，除非我们能够为各种场景设计合适的稀疏注意力内核。通过观察标准Transformer中不同头的注意力分布，[240]发现并非所有头都关注整个上下文（有些头只关注最近的标记），并提出为每个头学习动态注意力跨度，以降低计算和存储成本。然而，上述两项工作都只能关注过去连续的标记跨度。为了解决这个问题，[241]引入\(\alpha\) - entmax来代替softmax，使低评分的单词精确地获得零权重，从而实现更灵活的稀疏注意力。

    基于窗口的方法：与上述方法不同，基于窗口的方法将输入划分为单独的局部窗口，使每个标记仅关注窗口内的项目（图6 (c)），从而降低计算复杂度。早期的一种方法 [243]通过将Q、K和V矩阵划分为n个块（如果不能整除则进行填充），并通过移动一个位置在每个块内计算注意力，实现了\(O(\frac{N^{2}}{n})\) 的复杂度。这种方法比Sparse Transformer更容易实现。然而，值得注意的是，在实践中n通常设置为2或3以保持性能，这导致实际加速效果不佳。为了解决这个问题，[244]使用扩张滑动窗口来增加感受野，同时不增加计算量，并通过为预选的输入位置添加 “全局注意力”（图6 (d)）来提高性能。这里，k表示滑动窗口的大小，m表示预选位置的数量。然而，其扩展实现需要高效的带状矩阵乘法支持，使用朴素的CUDA内核只能达到与标准自注意力相同的运行速度。因此，在实践中，它仅在内存占用上与理论复杂度一致，但实际运行速度与理论复杂度存在差距。类似地，[246]建立了一种由三个主要组件组成的稀疏注意力模式：全局注意力，即一个全局标记集，该集合内的标记关注整个序列，且序列中的所有标记都关注该集合；局部注意力，即所有标记关注其周围的窗口集w；随机注意力，即所有标记关注一个随机标记集\(r^{-}\) 。值得注意的是，BigBird的实际运行速度与理论复杂度也存在差距，与[244]类似。除了上述方法，一些方法 [242,249]让每个标记直接关注近处的位置，并间接关注远处的位置。这种方法与上述基于窗口的方法非常相似，但在实现 “全局注意力” 的间接方式上有所不同。因此，我们在此介绍。[242]基于先前的观察，即元素之间距离越近，注意力得分越高，距离越远，注意力得分越低，提出了一种新的架构BP - transformer（BPT）。它将注意力计算视为一个图神经网络，并通过二分划分（BP）将输入序列划分为不同的多尺度空间，构建基于二叉树的注意力模式。每个叶节点代表一个标记，每个标记根据目标距离关注不同尺度的节点，从而将注意力的复杂度降低到\(O(k N log (N / k))\) ，其中k是一个控制注意力密度的超参数。[249]的核心思想与BPT非常相似，即让每个标记能够直接或间接关注所有其他项目。不同之处在于，它将注意力机制视为一个条件期望问题。
    基于数据的方法：与上述需要手动设计稀疏模式的方法不同，基于数据的方法 [245,247,248,250]使用适当的算法，使每个标记能够自动快速地找到最相关的项目来计算注意力。这些方法的最大优点是数据感知性，有效地避免了在不同任务和数据情况下需要手动重新设计稀疏模式的缺点，而且手动设计很难获得最优解。Reformer [245]通过使用局部敏感哈希快速找到相似向量，实现了高效的稀疏注意力计算，将复杂度降低到\(O(N log (N))\) 。同时，Reformer还使用了可逆层和FFN层中的分块等技术，在训练期间显著降低了内存使用。然而，这种权衡可能也会减慢训练速度。此外，为了避免哈希错误，Reformer需要进行多轮哈希，削弱了其最终的效率优势。与Reformer类似，[250]将自注意力视为一个路由问题。具体而言，它基于k - 均值聚类，通过让模型学习选择稀疏的单词示例簇，使查询和键能够在同一组簇质心向量上聚类。这样每个查询\(Q_{i}\) 仅关注与其属于同一簇的键。为了确保性能，它将簇的数量设置为\(\sqrt{N}\) ，从而将注意力复杂度降低到\(O(N \sqrt{N})\) 。其他与基于输入的稀疏注意力相关的工作有SAC [248]和SSA [247]。其中，SAC将输入视为一个图，并使用LSTM边预测器来学习标记之间的边。图中的节点代表标记，边代表注意力关系。它还使用强化学习来训练这个边预测器。然而，LSTM存在局限性，例如缺乏并行性和表达长期依赖关系的能力有限。可能有更好的方法来构建边预测器。另一方面，SSA基于内部表示的可微排序，并引入了一个元排序网络，该网络可以学习生成序列的潜在排序。它允许我们在给定排序序列后仅使用局部窗口进行准全局注意力，提高了注意力模块的内存效率。
2. 线性近似注意力：标准注意力可以表示为：
\(Attention(Q, K, V)=softmax\left(Q K^{T}\right) V\) (28)
由于\(Q K^{T}\)在序列长度和内存复杂度方面是二次的，这严重限制了注意力在长序列场景中的应用。因此，已经提出了几种致力于线性化注意力计算的方法来解决这个困境。根据这些方法的特点，我们将它们分为基于结合律的方法和基于低秩的方法。
    基于结合律的方法：自然的想法是，如果我们能够利用矩阵乘法的结合律先计算\(K^{T} V\) ，就可以在注意力计算中实现线性复杂度。然而，由于softmax的存在，我们无法轻易实现这一点。对于注意力结果中的每一行i，我们可以等效地表示为：
\(Attention (Q, K, V)_{i}=\frac{\sum_{j = 1}^{n} sim\left(q_{i}, k_{j}\right) v_{j}}{\sum_{j = 1}^{n} sim\left(q_{i}, k_{j}\right)}\)
其中\(sim(q_{i}, k_{j}) = e^{q_{i} k_{j}^{T}}\) ，它实际上是\(v_{j}\) 的加权平均，权重由\(e^{q_{i} k_{j}^{T}}\) 给出。一个自然的想法是，如果我们能够找到两个函数\(\phi_{1}(x)\)和\(\phi_{2}(x)\) ，使得：
\(sim\left(q_{i}, k_{j}\right)=\phi_{1}\left(q_{i}\right) \phi_{2}\left(k_{j}\right)^{T}\)
并且始终满足\(sim(q_{i}, k_{j})>=0\) ，同时还满足：
\(\left(\phi_{1}\left(q_{i}\right) \phi_{2}\left(k_{j}\right)^{T}\right) v_{j}=\phi_{1}\left(q_{i}\right)\left(\phi_{2}\left(k_{j}\right)^{T} v_{j}\right)\)
那么，我们就可以实现线性注意力。基于这个想法，已经提出了许多不同的线性注意力方法 [251,252,253,254,255,256]。具体而言，[251]通过构造：
\(\phi_{1}(x)=\phi_{2}(x)=elu(x)+1=\begin{cases}1 + x & x \geq 0 \\ e^{x} & x < 0\end{cases}\) (32)
来实现这一点。Performer [252]也通过核函数方法实现了线性注意力。它提出了一种FAVOR + 方法，巧妙地使用随机投影将输入特征正交投影。在不依赖任何先验且不损失准确性的情况下，成功实现了线性注意力。具体而言，对于函数\(f_{1}, \ldots, f_{l}: \mathbb{R} \to \mathbb{R}\) 、函数\(g: \mathbb{R}^{d} \to \mathbb{R}\) 和确定性向量\(\omega_{i}\) 或\(\omega_{1}, \ldots, \omega_{m} \stackrel{ iid }{\sim} D\) （对于某个分布\(D \in P(\mathbb{R}^{d})\) ），取\(\phi\) 的形式为：
\(\phi(x)=\frac{h(x)}{\sqrt{m}}\left(f_{1}\left(\omega_{1}^{\top} x\right), \ldots, f_{1}\left(\omega_{m}^{\top} x\right), \ldots, f_{l}\left(\omega_{1}^{\top} x\right), \ldots, f_{l}\left(\omega_{m}^{\top} x\right)\right)\)
为了更好地描述\(\phi\) 中的\(f_{i}\) 、\(h\) 和\(\omega_{i}\) ，对于原始注意力矩阵A中第i行和第j列的元素\(A(i, j)=\exp (q_{i} k_{j}^{T})\) ，我们给出其广义定义：
\(SM(x, y) \stackrel{ def }{=} \exp \left(x^{\top} y\right)\)
事实上，早在[257]中就有对\(SM (x, y)\) 的近似表达式，其中\(h(x)=\exp (\frac{\|x\|^{2}}{2})\) ，\(l = 2\) ，\(f_{1}=\sin\) ，\(f_{2}=\cos\) 。由于先前的方法中出现了\(\sin\) 和\(\cos\) 三角函数，计算结果中可能会出现负数等不稳定情况，Performer提出了另一种更稳定的近似：
\(\begin{aligned} & SM(x, y)=\mathbb{E}_{\omega \sim \mathcal{N}\left(0, I_{d}\right)}\left[\exp \left(\omega^{\top} x-\frac{\| x\| ^{2}}{2}\right)\right. \\ & \left.\exp \left(\omega^{\top} y-\frac{\| y\| ^{2}}{2}\right)\right]=\Lambda \mathbb{E}_{\omega \sim \mathcal{N}\left(0, I_{d}\right)} \cosh \left(\omega^{\top} z\right) \end{aligned}\) (35)
这里\(\Lambda=\exp (-\frac{\|x\|^{2}+\|y\|^{2}}{2})\) ，\(x, y \in \mathbb{R}^{d}\) ，\(z = x + y\) ，\(\cosh\) 是双曲余弦函数。这相当于使：
\(h(x)=\exp \left(-\frac{\| x\| \| ^{2}}{2}\right)\) ，\(l = 2\) ，\(f_{1}(x)=\exp (x)\) ，\(f_{2}(x)=\exp (-x)\)
然而，为了确保准确性，随机样本的数量m通常大于特征维度d，这意味着在处理短序列时，Performer的表现可能不如标准Transformer。只有当序列相对较长时，其优势才能充分发挥。同样，[256]通过双softmax方法实现线性近似注意力：
\(Attention(Q, K, V) \approx softmax_{1}(Q) softmax_{2}(K) V\) (37)
其中，\(softmax1\)、\(softmax2\)分别指在第一（\(N\)）维和第二（\(d\)）维上的softmax操作。然而，直接分别对\(Q\)、\(K^{T}\)进行softmax操作（即不进行相似性（内积）计算），给人的感觉与注意力机制背道而驰。[253]在此基础上进行改进，首先将\(Q\)、\(K\)分别视为\(n\)个\(d\)维向量，然后将它们聚类为分别由\(m\)个聚类中心组成的矩阵\(\bar{Q}\)、\(\tilde{K} \in \mathbb{R}^{m ×d}\) 。此外，在中间插入一个矩阵\(M \in \mathbb{R}^{m ×m}\) ，使得最终的注意力计算可以表示为：
\(\begin{aligned} & Attention(Q, K, V) \approx softmax\left(Q \tilde{K}^{\top}\right) \\ & \left(softmax\left(\tilde{Q} \tilde{K}^{\top}\right)\right)^{-1} softmax\left(\tilde{Q} K^{\top}\right) V \end{aligned}\)
这更接近标准注意力。

最近，HyperAttention [255]基于核密度估计（KDE）简化了现有算法，通过汉明排序局部敏感哈希识别注意力矩阵中的主要元素，并提出了一种简单的线性时间注意力近似算法。该算法可以在确保注意力谱特性并支持因果掩码的同时，实现广泛的线性近似注意力。值得注意的是，HyperAttention在使用因果掩码和不使用因果掩码两种情况下的加速效果可能相差数十倍。同时，如果HyperAttention完全取代所有层的注意力，模型性能将显著下降，因此该方法仍需在速度和性能之间进行平衡。
    基于低秩的方法：其他实现线性注意力的方法[258,259]是通过利用低秩特性。Linformer [258]观察到Transformer模型中注意力矩阵的归一化累积奇异值在多个任务中呈现低秩特性。基于这一观察，Linformer保留了原始的缩放点积注意力公式，但在计算注意力之前，使用两个矩阵\(E\)、\(F \in \mathbb{R}^{m ×n}\)对\(K\)和\(V\)进行投影，从而实现线性近似注意力计算，形式上表示为：
\(Attention(Q, K, V) \approx softmax\left(Q(E K)^{T}\right) F V\)
为了保持其性能，必须将\(m\)的值设置得足够高。然而，这可能导致Linformer在处理短序列时相对较慢。因此，Linformer的理论复杂度和实际应用之间可能存在显著差异。

最近，Transformer - VQ采用了独特的视角，在注意力计算中对键矩阵\(K\)进行向量量化（VQ）。这是通过使\(K\)中的每个向量最接近\(C\)中的向量来实现的，其中\(C\)是训练参数和VQ码本。VQ可以用数学表示为：\(\widehat{K}=V Q(K, C)\) ，\(K \in \mathbb{R}^{n ×d_{k}}\) ，\(C \in \mathbb{R}^{c ×d_{k}}\) 。由于\(\widehat{K}\)中的每个向量都来自\(C\)，我们可以首先计算\(Q C^{T}\) ，由于\(C\)的大小固定，所以这是线性的。Transformer - VQ巧妙地构造了一个\(\Delta \in{0,1}^{n ×c}\) ，使得：
\(\exp \left(Q K^{T}\right) V=\exp \left(Q C^{T} \triangle^{T}\right) V=\exp \left(Q C^{T}\right)\left(\triangle^{T} V\right)\)
此计算的复杂度为\(O(n c d_{k}+n c d_{v}+n c d_{v}) = O(n)\) ，实现了线性注意力。此外，该方法可以自然地应用于自回归任务，使其成为一种很有前景的方法。
3. FlashAttention：与之前的近似注意力方法不同，FlashAttention专注于减少内存访问开销，并取得了巨大成功。它在减少注意力内存占用的同时，实现了训练和推理的加速。更重要的是，它不是一种近似注意力方法，这意味着其计算结果与标准注意力结果完全相同。

其核心是分块（tiling），即将计算中涉及的矩阵分块传输到共享内存中，以提高整体读写速度。例如，如图7所示，假设我们现在需要计算矩阵\(A\)与矩阵\(B\)相乘结果的上半部分\(c_{0}\) 。对于标准矩阵乘法，有\(C_{0}=(A_{0} B_{0}+... + A_{0} B_{3}) concat(A_{1} B_{0}+... + A_{1} B_{3})\) 。而对于分块矩阵乘法，\(C_{0}=(A_{0} B_{0}+A_{0} B_{1}) concat(A_{1} B_{2}+A_{1} B_{3})\) ，将内存访问减少到标准矩阵乘法的一半。

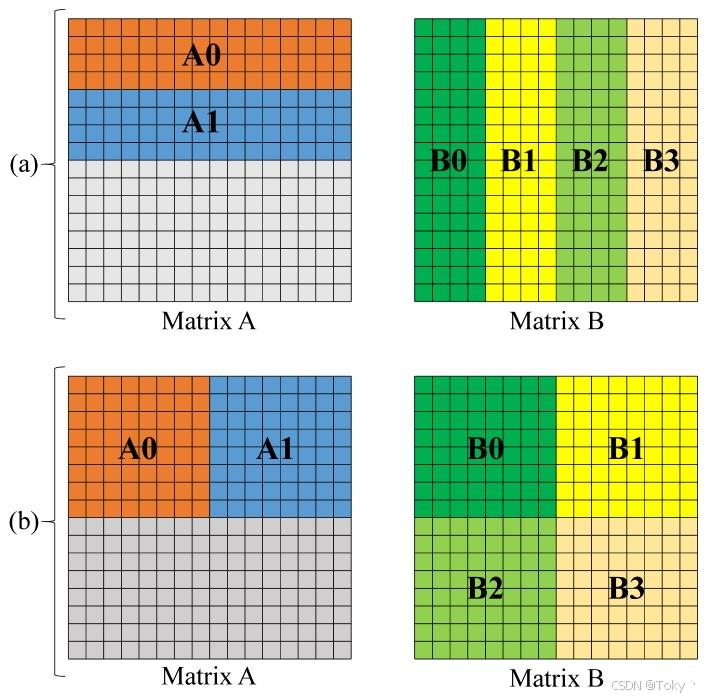
图7：(a)标准矩阵乘法；(b)分块矩阵乘法

实际上，在朴素的矩阵乘法版本中，每次计算时仅从内存中读取两个矩阵的一行和一列。内存访问效率非常低，这里的两个示例分别从矩阵\(A\)和\(B\)读取相同数量的元素，只是为了便于比较。对于矩阵乘法，我们可以直接使用分块方法，但注意力计算中存在softmax操作，且softmax的分母包含与所有元素相关的求和项，因此将分块应用于注意力计算的真正困难在于softmax的分块。

对于标准注意力，我们通常使用数值稳定的softmax：
\(Softmax\left(x_{i}\right)=\frac{e^{x_{i}-m}}{\sum_{j = 1}^{N} e^{x_{j}-m}}\)
其中\(m\)表示所有\(x_{i}\)中的最大值。为了得到最终结果，我们需要进行三轮迭代：遍历所有\(x_{i}\)以找到最大值\(m\)；遍历所有\(x_{i}\)以找到\(sum =\sum_{j = 1}^{N} e^{x_{j}-m}\) ；计算每个\(Softmax(x_{i})\) 。

由于每轮迭代都依赖于前一轮的结果，因此计算不能分块独立进行。一种现有方法是定义一个序列\(l'\)：\(l_{i}'=\sum_{j = 1}^{i} e^{x_{j}-m_{i}}\) ，从而有：
\(\begin{aligned} l_{i}' & =\sum_{j = 1}^{i} e^{x_{j}-m_{i}}=\left(\sum_{j = 1}^{i - 1} e^{x_{j}-m_{i}}\right) e^{m_{i - 1}-m_{i}}+e^{x_{i}-m_{i}} \\ & =l_{i - 1}' e^{m_{i - 1}-m_{i}}+e^{x_{i}-m_{i}} \end{aligned}\)
这是通过拼凑出\(\sum_{j = 1}^{i - 1} e^{x_{j}-m_{i}}\) 并用\(l_{i - 1}'\)的增量计算来替换它，很明显，在得到这一步之后，我们的序列可以与\(i\)和\(m\)在同一轮迭代中计算，最后，\(i_{n}'\)将等同于\(l\) ，通过这种方式我们可以将三轮迭代减少到两轮。然而，两步迭代仍然是耦合的，不能分块进行单独计算。受先前推导的启发，FlashAttention推导出了在一轮迭代后获得最终\(O\)矩阵的方法。矩阵\(o\)中的一行是\(V\)和Softmax结果的加权和，可以表示为：
\(o_{i} \leftarrow \sum_{j = 1}^{N}\left(\frac{e^{x_{j}-m_{N}}}{l_{N}} V[j,:]\right)\)
使用相同的技巧，引入一个单独的\(o\)序列，并让它使用局部的\(m_{i}\)和\(i_{i}\)参与计算：
\(o_{i}' \leftarrow \sum_{j = 1}^{i}\left(\frac{e^{x_{j}-m_{i}}}{l_{i}'} V[j,:]\right)\)
很容易看出，对于\(N\) ，\(O_{i}\)等于\(o_{N}'\) ，问题转化为如何从公式中拼凑出\(\sum_{j = 1}^{i - 1}(\frac{e^{x_{j}-m_{i - 1}}}{l_{i - 1}'} V[j,:])\) 并用\(o_{i - 1}'\)替换它：
\(\begin{aligned} o_{i}' & =\sum_{j = 1}^{i}\left(\frac{e^{x_{j}-m_{i}}}{l_{i}'} V[j,:]\right) \\ & =\left(\sum_{j = 1}^{i - 1} \frac{e^{x_{j}-m_{i - 1}}}{l_{i - 1}'} V[j,:]\right) \frac{e^{m_{i - 1}}}{e^{m_{i}}} \frac{l_{i - 1}'}{l_{i}'}+\frac{e^{x_{i}-m_{i}}}{l_{i}'} V[i,:] \\ & =o_{i - 1}' \frac{l_{i - 1}' e^{m_{i - 1}-m_{i}}}{l_{i}'}+\frac{e^{x_{i}-m_{i}}}{l_{i}'} V[i,:] \end{aligned}\)
使用上述公式计算注意力只需要一轮迭代，因此我们可以分块计算以找到最终结果。FlashAttention - 2 [261]对此进行了改进，将公式(44)改进如下：
\(o_{i}'=o_{i - 1}' l_{i - 1}' e^{m_{i - 1}-m_{i}}+e^{x_{i}-m_{i}} V[i,:]\) (45)
与原始的\(o_{i}'\)相比，我们在最终计算\(o_{N}'\)时只需要再除以一个\(l_{N}'\)就可以得到正确结果，从而避免了中间的多步缩放除法操作。它还减少了内存写入开销。具体来说，在FlashAttention中，固定\(K_{j}\)、\(V_{j}\)枚举\(Q_{i}\)、\(O_{i}\)、\(l_{i}'\)、\(m_{2}\)进行计算；这样，对于每个计算得到的\(O_{2}\)我们都需要将其写回内存，这需要\(O(N^{2} d^{2} M^{-1})\)的写入复杂度，其中\(M\)表示共享内存的大小。在FlashAttention2中，我们固定\(Q_{i}\)、\(O_{i}\)、\(l_{i}'\)、\(m_{\bar{i}}\)枚举\(K_{j}\)、\(V_{j}\) ，这样\(O_{i}\)的最终结果可以一次性计算出来然后写回内存，写入复杂度降低到\(O(N d)\) 。此外，它还对序列长度维度进行了并行化；当批量大小和头数较小时，它增加了序列长度上的并行度以提高GPU利用率，显著提高了计算速度。

一般来说，高效注意力优化方法主要包括稀疏注意力、线性化注意力和FlashAttention。然而，许多高效注意力方法的实际效果和理论效果之间往往存在差距，例如，许多稀疏注意力方法由于不连续的内存访问，在实践中很难达到理论效果，这主要是因为我们在改进方法时没有考虑现有硬件的特性。

 6.2 神经架构搜索

尽管大型语言模型的压缩和加速方法已经取得了显著进展，但目前许多决定模型最终形态的超参数仍然需要通过手工设计来确定。这种手工设计方法通常需要设计者具备大量的专业知识和经验，同时还存在训练时间长、成本高的问题。在这种困境下，一种有前景的解决方案是神经架构搜索（Neural Architecture Search，NAS）[262,263,264,265,266,267,268,269,270]。为了简单起见，接下来我们将介绍其中一项具有代表性的工作。

Transformer模型的高计算成本使得它难以部署在一些硬件设备上，并且在资源有限的硬件设备上实现低延迟推理也很困难。HAT [262]应运而生。HAT的思路是在给定延迟要求的情况下，搜索满足要求（给定硬件条件和资源）的最佳性能模型结构参数。然而，从头开始搜索模型结构并进行训练和评估成本高昂且速度缓慢。HAT通过构建一个超级Transformer来避免昂贵的重新训练，该超级Transformer通过共享权重近似包含搜索空间中的所有子Transformer模型。同时，HAT训练一个延迟预测器，通过离线方法预测延迟，这进一步加快了搜索速度。此外，它观察到了几个重要特性：
第一，关注多个编码层对解码层有益。
第二，不同硬件对模型有不同的偏好，GPU更喜欢浅而宽的Transformer，而ARM CPU更喜欢窄而深的Transformer。

总体而言，HAT为不同硬件条件和延迟要求下的Transformer模型提供了一种高效的NAS方案。同时，它可以与其他压缩加速方法很好地结合，因为它在不改变模型架构的情况下，为给定条件找到了合适的模型结构参数。

 7 动态网络

扩大语言模型的规模已被证明是提高其在自然语言处理（NLP）任务上性能的有效方法[271,272]。然而，随着模型规模的扩大，计算成本和内存需求大幅增加，这成为大型语言模型发展的主要挑战。为了解决这些问题，同时仍然利用模型规模扩大带来的优势，动态神经网络（DyNNs）针对每个输入仅激活网络的一个子集进行处理，使整个模型在资源受限的环境中更灵活、高效地满足计算需求。在NLP领域和大型语言模型的范畴内，目前关于DyNNs的研究主要包括以下三种方法：早期退出、级联推理和专家混合（MoE）。

早期退出旨在在深度神经网络（DNNs）的早期层动态终止推理过程，从而降低计算成本并提高响应速度[273]。其基本思想是，对于不太复杂的单词，往往可以在网络的早期层准确完成预测[274]。这些方法通常在网络中集成一系列内部分类器，在推理过程中提供早期退出的信号。已经提出了各种退出标准[275,276,277,278,279,280,281,282]。这一系列工作主要集中并应用于小型或中型语言模型，如Bert。然而，其准确性可能不足以支持通用大型语言模型在更复杂和现实场景中的应用。

级联推理利用一系列不同规模的语言模型来处理具有不同复杂程度的请求。Tabi [283]提出了一种具有多级推理模型和基于概率的调度器的推理系统，用于确定输入查询的处理策略，平衡准确性和效率。FrugalGPT [284]学习自适应地对来自不同数据集和任务的查询进行分类，并将它们导向合适的大型语言模型API组合。EcoAssistant [285]和[286]都使用查询缓存来参考历史数据以实现更快的响应，并使用层次化的大型语言模型来处理不匹配的新查询。Mixture - of - Thoughts [287]将较弱大型语言模型答案的一致性作为问题难度的指标，以决定是否使用更强的大型语言模型。一般来说，这一系列工作最近才出现，为更高效的大型语言模型系统的发展展示了一个有前景的方向。

与上述两种方法相比，MoE的研究在包括NLP在内的多个机器学习领域有着广泛的历史。MoE通过多个子网络对前馈网络（FFN）进行水平扩展，在单次前向传递中仅激活其中一个或几个子网络。它被广泛应用于当今大型语言模型的架构中[288,289]，以提供高效且强大的服务。因此，在本节的其余部分，我们将深入探讨MoE领域。7.1节首先介绍MoE的基本概念，随后对当代将MoE融入大型语言模型的研究进行广泛综述，包括算法和架构设计、训练策略以及实际应用。7.2节简要回顾一些将MoE与之前讨论的模型压缩和加速技术相结合的代表性研究，突出其在开发更全面、更具成本效益的大型语言模型系统方面的潜力。

 7.1 专家混合

MoE的最早概念可以追溯到三十年前[298,299]，但它首次通过稀疏门控展示了在不付出成比例计算开销的情况下大幅提高模型容量的有效性[292]。在稀疏MoE模型中，模型参数的一个子集被划分为一组\(N\)个专家网络\(\{E_{i}(\cdot)\}_{i = 1}^{N}\) ，每个专家网络对输入独立进行操作，且权重不共享。在训练和推理过程中，每个输入示例\(x\)（即语言模型中的一个标记表示）将在训练和推理过程中，每个输入示例\(x\)（即语言模型中的一个标记表示）将通过门控函数\(G(\cdot)\)被路由到特定的专家网络，门控函数\(G(\cdot)\)的输入也是\(x\)，输出是一个稀疏的\(n\)维向量。MoE模块的最终输出\(y\)是一个加权组合，可以表示为：
\(y=\sum_{i=1}^{N} G(x)_{i} E_{i}(x)\)

基于\(G(x)\)的稀疏性，只要\(G(x)_{i}=0\)，我们就可以跳过\(E_{i}(x)\)的计算。由于每个输入仅激活部分模型参数，并且所有专家都有被不同样本利用的潜力，因此MoE模型在理论上具有很强的学习能力，并且与密集模型相比，推理速度更快。随着Transformer [1]成为语言模型的标准选择，将MoE引入Transformer的最常见方法是用MoE层替换某些块的前馈层，其中每个专家本身就是一个常规的Transformer前馈网络。图8展示了一个MoE层的示例。通过增加专家数量，参数规模可以从数亿增长到数百亿甚至数万亿，以匹配大型语言模型的规模。表征一种MoE方法主要有三个关键要素：（1）路由方法决定每个输入在MoE层中的路由位置和方式，这是MoE算法中最关键的要素。（2）MoE模型架构讨论构建更高效且参数利用更合理的扩展模型时常见或特定的设计选择。（3）有时需要特殊的训练策略来适应基于学习的路由方法带来的不确定性。我们在表5中总结了一些具有代表性的MoE方法。

图8：集成了MoE层的Transformer块示意图

表5：各种专家混合（MoE）方法总结。对于最大规模的模型，我们列出总参数数量以及每层MoE中的专家数量。对于使用共享专家的方法[290,291]，我们同时列出（用于共享的专家数量 + 用于路由的专家数量）。

 7.1.1 路由方法

对于一个MoE系统，影响其性能的最关键因素以及主要设计关注点是确保专家之间的负载均衡。

在标准的分布式训练设置中，同一层的专家分布在多个设备上。在大多数情况下，每个专家都是一个简单的前馈网络（FFN），并进行并行计算。每个专家在单次前向传递中能够处理的最大token数量（也称为专家容量）受其所在设备的内存限制。通常情况下，如果没有特定的算法或架构设计，由于门控函数的稀疏性，同一批次中的token会不均匀地分配到各个专家。因此，如果过多token被路由到同一个专家，超过其容量，就会导致溢出问题。溢出部分的计算将被跳过，这些token将通过残差连接直接传递到下一层。因此，专家之间的负载不均衡会导致token处理不足，并且对于有空余插槽的专家来说，会造成计算和内存的浪费。

除了性能下降之外，专家之间的负载不均衡还可能导致一种自我强化现象，通过训练内在地限制MoE系统的能力。这种现象表现为门控网络收敛到一种状态，总是为相同的少数专家产生较大的权重，这些专家会用大量数据进行快速训练，并且更受门控网络的青睐。结果，其余专家训练不足且未得到充分利用，导致原始的MoE网络退化为仅由少数活跃专家组成的较小网络。

除了负载不均衡问题，还有一些方法致力于减轻MoE稀疏性带来的其他负面影响，例如不稳定的路由或稀疏性与准确性之间的权衡。

基于每种方法解决的主要问题，我们将现有的路由方法分为以下两组进行回顾。
1. 实现负载均衡：大多数路由方法在每个MoE层中应用一个额外的可学习门控网络。一个简单且被大多数工作采用的选择是使用一个具有可训练矩阵\(W \in \mathbb{R}^{d ×N}\)的线性层，其中\(d\)是模型维度，\(N\)是专家数量，然后接一个非线性函数，如softmax或sigmoid。\(W\)的\(N\)列\(\{w_{1}, \cdots, w_{N}\}\)也可以看作是\(N\)个专家的嵌入，在一些工作中可以看到这种表述。对于每个token\(x \in \mathbb{R}^{d}\)，\(x\)与第\(i\)个专家之间的路由分数由点积相似性度量\(s_{i}=x \cdot w_{i}\)给出。为了给门控网络引入稀疏性，即每个MoE层仅使用\(k\)个专家（\(k \ll N\)），对于token\(x\)，仅选择\(\{s_{i}\}_{i = 1}^{N}\)中值最高的前\(k\)个专家（索引集为\(\mathcal{T}\)）。一般来说，如果专家\(i\)被激活，其门控值由下式给出：
\(G(x)_{i}= \begin{cases} \frac{\exp (s_{i})}{\sum_{j \in \mathcal {T}} \exp \left(s_{j}\right)}, & \text{softmax门控}, k>1 \\ \frac{\exp (s_{i})}{\sum_{j=1}^{N} \exp \left(s_{j}\right)}, & \text{softmax门控}, k = 1 \\ \sigma(s_{i}), & \text{sigmoid门控} \end{cases}\)
其中\(\sigma(\cdot)\)是sigmoid函数。需要注意的是，对于softmax门控，top - 1方法的公式略有不同，以确保\(G(x)\)非平凡。上述思路最早在[292]中提出，并应用于LSTM模型[300]。为了减轻自我强化问题，他们在路由分数中添加了一个可调节的高斯噪声，并采用了两个额外的损失项，以鼓励专家之间的路由分数和选择率更加均衡。GShard [293]通过用MoE层替换每隔一个前馈层，将MoE集成到Transformer中，使用top - 2门控。他们提出了几种确保负载均衡的策略，包括（1）将token划分为组，并限制每个专家从单个组中接收的token数量；（2）一个被后续工作广泛采用的辅助损失项[294,301,302]；（3）一种随机路由策略。为了进一步使计算成本与普通Transformer的计算成本保持一致，Switch Transformer [294]使用top - 1门控，将每个token仅路由到一个专家。

上述研究主要提出了一些中间策略，如辅助损失项，以在训练期间促进负载均衡。其他研究则旨在改进门控函数，直接对专家之间的负载进行正则化，甚至保证完美的负载均衡。BASE Layer [303]将token到专家的分配表述为一个线性分配问题，在满足每个专家必须接收等量token的约束下，最大化专家与其分配token之间的分数。Expert Choice [295]是另一种保证完美负载均衡且无需额外正则化的路由策略。与让token选择前\(k\)个专家不同，每个专家根据路由分数选择前\(k\)个token。因此，每个专家可以有完全相同的工作量，并且每个token可以由不同数量的专家处理。Clark等人[304]提出了一种使用强化学习的路由算法，其中每个路由器被视为一个策略，其动作和奖励分别由专家的选择和预测正确输出token的概率定义。除了使用可学习的门控网络，一些研究还实施了不可学习的策略来调节专家之间的负载分布。Hash Layer [305]使用一个无参数的哈希函数，用预定义的固定映射从token到特定专家来代替动态门控，从而消除了负载不均衡问题。MoWE [306]根据辅助词汇映射将每个单词路由到一个特定的专家，并确保分配给每个专家的单词在预训练数据中的频率大致相同。受Hash Layer的启发，PanGuΣ [307,308]部署了一种两级路由，首先根据领域将每个token映射到一组候选专家，然后使用随机哈希从该组中选择一个特定的专家进行处理。THOR [309]也通过一种无参数的方法简化了门控过程，在训练迭代中从每一层随机选择一对专家，并将整个批次的token分配给这些专家。

到目前为止我们描述的方法只有在设备资源充足（即不遇到溢出问题）的情况下才能充分发挥作用。在更现实的场景中，必须采取额外的策略来处理溢出。最简单的解决方案是停止向工作量已满的专家分配token。然而，这样做的话，根据批次是按序列长度还是批次维度进行扁平化，只有输入句子的前缀或批次维度中索引较小的句子会被处理，这会导致有偏差的选择和训练或推理数据的利用不足。为了解决这个问题，Z - code [310]和BASE [303]提出对扁平化批次中的输入token进行洗牌，以消除token被选择的概率与其位置之间的关联。在视觉Transformer领域，V - MoE [311]引入了批次优先路由算法（Batch Prioritized Routing，BPR），该算法为每个token额外计算一个优先级分数（例如，token与所有专家之间路由分数的最大值），并在分配前对token进行相应排序。因此，只有不重要的token会被丢弃。STMoE [312]发现BPR对语言模型也有益，特别是在低资源环境中，专家容量甚至小于每个专家平均接收的token数量的情况下。需要注意的是，BPR只能应用于编码器 - 解码器模型的编码器端，因为编码器的输入不是自回归的，因此可以相互可见，否则模型可能会利用未来的token信息进行作弊。
2. 具有稀疏性的有效路由：虽然稀疏性在大规模MoE系统中限制了计算成本，但它通常会限制网络的能力并阻碍收敛，因为路由动态不稳定。DeepSpeed - MoE [290]观察到增加每个token经过的专家数量有助于提高准确性。为了在保持top - 1门控计算成本的同时利用这一特性，他们提出了Residual - MoE，通过为每个token固定一个专家并改变第二个专家，以实现使用2个专家的好处。DeepSeek - MoE [291]采用了相同的方法，利用一组固定的共享专家来捕获和整合通用知识，并通过一组不同的路由专家来实现知识的专业化。M6 - T [296]也注意到top - k门控相对于top - 1的优势。他们提议将专家划分为\(k\)个组，并并行执行\(k\)次top - 1路由，以匹配top - 1门控的效率。为了确保在稀疏设置下每个专家都能接收丰富多样的token，MoEC [302]通过设计损失项鼓励专家形成聚类结构，使相邻专家之间的路由概率更接近，并在全局top - 1门控之前随机丢弃每个聚类中的一些专家。

除了稀疏性，DSelect - k [313]注意到top - k门控方法的不连续性，并认为这可能会在使用基于梯度的方法进行训练时导致收敛和性能问题。他们提出了一种连续可微且稀疏的门控函数，在训练开始时密集地选择专家，但通过添加正则化项快速收敛到稀疏的专家选择。XMoE [301]指出当前的路由机制倾向于将token表示推向专家嵌入，这可能会损害表示能力。他们提议在低维空间中计算token与专家之间的路由分数，并进行额外的归一化和可学习的门控温度调整。ST - MoE [312]对稀疏MoE模型的训练稳定性和微调质量进行了广泛研究。他们将稀疏模型的训练过程视为质量 - 稳定性的权衡：各种稳定性技术，如随机失活（dropout）和梯度裁剪，虽然可以增强训练稳定性，但往往会以模型质量为代价。因此，他们提出了路由器z - 损失来解决不稳定性问题和质量下降问题。

 7.1.2 MoE模型架构

在本部分中，我们讨论如何将MoE层融入基于Transformer的模型中，例如专家层的频率和专家数量，这些因素会显著影响模型的规模和整体性能。

在Transformer中，稀疏模型通常从一个密集模型开始，通过以固定间隔或启发式地替换或插入MoE层来进行扩展。大多数大型稀疏专家模型[293,294,295,314,315]采用的一种常见设计是用MoE层替换每隔一个Transformer块的前馈组件（即频率为0.5）。也有其他频率被采用，例如[312]中为0.25（即每四个FFN层替换一个），以及1.0（即每层都放置）。一般来说，实验[304]表明，频率在0.5 - 1.0之间效果较好，较低的频率会损害性能。然而，也有一些工作[301,302,303,305,316]通过在基线模型中不均匀地分布MoE层，引入固定数量的专家层。例如，BASE [303]仅在中间层之后插入一个由堆叠FFN组成的大型MoE层。

至于每层的专家数量，虽然在大多数情况下使用更多的专家会持续带来质量提升，但早期工作[293,294]也报告了收益递减的情况。进一步的分析[304,312]也指出，随着基础模型规模的增加，路由带来的增量收益会急剧减少。[304]建议每层固定数量的专家为\(\{64, 128\}\)，并且这一建议在许多稀疏大型语言模型[312,314,317]中得到了实践。此外，DeepSpeed - MoE [290]对在所有MoE层中设置相同数量专家的标准MoE架构提出了质疑。他们的实验表明，在更深的层中使用更多的专家能更有效地提升性能。因此，他们引入了一种金字塔结构，仅在最后两层使用更多的专家，并在参数更少的情况下实现了与标准MoE模型相当的结果。

上述工作都是基于统一的Transformer块，通过交错密集层和稀疏层构建模型。Brainformer [297]受到EfficientNet [318]和sandwich transformer [319]成功的启发，探索了一种具有稀疏层的非均匀架构。一种进化搜索算法被应用于在由不同层类型（即自注意力、MoE和密集FFN子层）、交错顺序和超参数设置（如模型维度和注意力头数量）组成的搜索空间中，探索最佳的Brainformer块架构。整个网络根据不同的规模堆叠不同数量的块。实验结果表明，与它的GLaM [314]对应模型和由神经架构搜索（NAS）生成的密集模型Primer [320]相比，Brainformer在效率和容量方面都具有明显优势。

 7.1.3 训练策略

现有的基于学习的路由方法通常从 scratch 开始联合训练门控网络和专家网络。由于MoE层的参数是随机初始化的，训练初期的路由行为可以看作是随机路由，token与专家之间的对应关系非常不稳定。因此，MoE模型需要更长的时间来收敛，并且存在强化不当路由行为的潜在风险，最终会限制模型质量。

为了解决这个问题，[316,322]中引入了一种两阶段训练策略，将门控网络和专家网络的训练分开。在第一阶段，StableMoE [316]通过标准的MoE训练过程并添加平衡损失，学习一种平衡且一致的路由策略。在第二阶段，路由策略被冻结，为模型其余部分的训练提供稳定的token到专家的分配。实验证实，路由策略的一致性提高了收敛速度和最终性能。相反，EvoMoE [322]从训练一个共同的专家开始，然后在第一阶段进行多样化，在第二阶段学习门控网络并使网络稀疏化。通过这种方式，专家能够在早期得到充分训练，并且可以在利用专门化专家的基础上构建更合适的路由策略。

另一类工作通过在MoE层采用特殊的随机失活（dropout）[323]机制，来缓解由于大量参数与有限训练示例之间的不平衡导致的过拟合问题。例如，Switch Transformer [294]仅在专家内部增加随机失活率，称为专家随机失活（expert dropout），以帮助在训练数据极少的下游任务中提升性能。Gating Dropout [324]进一步推进了传统的随机失活，以减少在设备间分配token的通信成本，并在训练过程中提高性能。具体来说，他们允许token以一定概率忽略门控网络的分配，而是将其路由到同一设备上的专家。这也鼓励专家更稳健地发挥作用，并学习一种泛化能力。结果表明，Gating Dropout确实在实际运行时间方面加速了稀疏MoE模型的收敛，并提高了模型质量。

 7.1.4 MoE应用

MoE模型的成功推动了一系列工作，将稀疏MoE算法应用于实际的大型语言模型应用中，或者与其他模型压缩和加速技术相结合，以追求更高的效率。CPM - 2 [325]将BASE Layer [303]集成到其最大的中英双语模型中，该模型有1980亿参数。遵循GShard [293]，GLaM [314]训练了一系列仅解码器的稀疏MoE模型，其中最大的模型有1.2万亿参数，与密集的GPT - 3 [9]对应模型相比，在零样本、一样本和少样本学习能力方面表现更好。为了缩小高资源语言和低资源语言之间的性能差距，并突破200种语言的障碍，[317]开发了一种具有545亿参数的稀疏门控MoE模型，遵循[293]中的优化过程，为通用翻译系统开辟了一条有前景的道路。一篇关于GPT - 4技术细节的揭秘文章[288]证实了GPT - 4中部署了一个由16个专家组成的MoE模型。每个专家都针对特定领域或任务进行了微调，从而赋予GPT - 4多任务处理能力。Mixtral [289]基于Mistral 7B构建，用MoE层替换了所有FFN子块，每个MoE层由8个专家和一个top - 2门控网络组成。最终得到的Mixtral 8x7B在推理时仅使用1300万个活跃参数，但在多个基准测试中超过了Llama 2 70B [18]和GPT - 3.5。DeepSeekMoE [291]提出了一系列规模为20亿、160亿和1450亿的MoE模型以及对齐版本，以展示其MoE架构的适应性和通用性。OpenMoE [326]也发布了一套开源的MoE模型，基于STMoE [312]和Residual - MoE [290]的架构。此外，他们对MoE在训练过程中的路由行为进行了全面研究，并提供了一些见解。

 7.2 结合MoE与其他高效技术

专家混合（MoE）方法为构建更强大、高效的大型语言模型开辟了新途径。鉴于MoE类似于一种架构设计方法，并且与大多数模型压缩和加速技术正交，也有研究探索将其固有的稀疏性与其他优化策略（如剪枝、蒸馏和参数高效微调（PEFT））相结合的方法。在本节中，我们将审视这一领域中最具代表性的研究，并强调其在未来研究中的潜力。

 7.2.1 模型压缩

在稀疏MoE模型领域，现有的大多数工作可视为以内存消耗换取模型质量。为在保留大部分能力的同时减少内存占用，研究人员探索了多种将传统模型压缩技术引入MoE模型的方法。

Switch Transformer [294]率先尝试将大型稀疏模型蒸馏为小型密集模型。他们的研究结果表明，在将模型蒸馏为计算量（FLOP）匹配的密集变体时，对于预训练和微调任务，大约可以保留通过模型扩展所获得质量提升的30%。DeepSpeed - MoE [290]研究了将大型教师MoE模型蒸馏为较小的学生MoE模型（专家网络更浅）的潜力。此外，他们提出了一种阶段式知识蒸馏（stage - KD）训练策略（即在特定步骤停止蒸馏），以缓解由于学生模型专家容量有限而导致的欠拟合问题。

作为另一种重要的参数减少工具，MoE模型的剪枝旨在去除冗余或影响力较小的组件，通常是去除一部分不太重要的专家网络，同时对性能的影响最小化。Z - code [310]提出的剪枝假设是，在训练过程中不同专家可以专注于任务的不同方面，使得一部分专家在一定程度上足以胜任给定任务。Z - code尝试了两种专家选择方法：随机选择和基于验证集利用率的选择。Chen等人[327]观察到下游任务中专家贡献的长尾分布。与Z - code的方法不同，他们提议在微调过程中逐步去除大部分专家，只保留对目标下游任务最专业的那个。实验结果凸显了他们剪枝策略的有效性，在享受与普通密集模型相同推理资源消耗的同时，保留了MoE带来的99.3%的优势。作为一种替代方法，MPOE [328]引入了一种参数高效的MoE架构，通过将每个专家的参数矩阵分解为中心张量和辅助张量。中心张量被认为编码了原始矩阵中的大部分信息，这些信息在不同专家之间可能相似，因此适合在专家之间共享。而辅助张量则捕捉个体特征，作为对中心张量的补充。这种参数共享方法已被证明是有效的，在总参数减少27.2倍的情况下，性能优于Switch Transformer。

见证了MoE模型的巨大成功，也有研究致力于将稀疏性引入标准Transformer模型，以减少计算中涉及的参数数量，同时保留其表示能力。MoEBERT [329]将预训练的BERT [3]中的前馈网络改编为多个专家，在推理时仅激活一个专家以提高速度。为保留原始表示能力，他们在初始化MoEBERT时，根据重要性得分[330]在专家之间共享FFN中最重要的神经元。MoEBERT的训练采用了逐层蒸馏，最终得到的模型在性能上优于其他特定任务的蒸馏方法。MoEfication [331]旨在将FFN转换为MoE层的方法推广到各种Transformer模型。其核心思想是，大多数输入只会激活FFN中极少部分的神经元。为将前馈层划分为专家，将经常同时激活的神经元分组到同一个专家网络中。并且通过近似原始模型的计算来学习路由策略。为进一步降低标准Transformer的计算和内存需求，σ - MoE [332]和SwitchHead [333]借鉴MoE方法的原理，在前馈网络和注意力组件中引入额外的稀疏性。

 7.2.2 高效微调

为寻求更高效、强大的模型架构，研究人员还在探索将MoE方法与其他具有成本效益的技术（如Mixer [334]和参数高效微调（PEFT）方法）相结合。这些协作方法主要利用MoE提供的表达能力，同时大幅降低训练和计算成本。

稀疏混合器（Sparse Mixers）[335]用混合层和MoE子层替换了大部分自注意力子层，并用MoE机制在特征维度上进行路由，以确保来自同一句子的token被传递到同一个专家。SMLP [336]更进一步，用线性变换替换自注意力模块，同样采用了带有路由的MoE机制。AdaMix [337]提出了一种混合适配器（mixture of adapters）或混合低秩分解矩阵（mixture of low - rank decomposition matrices）的随机路由机制[309]，作为一种新颖的微调技术，以提升下游任务的性能。结果表明，AdaMix在自然语言理解（NLU）和自然语言生成（NLG）任务上均优于当前最优的参数高效微调算法，甚至超过了全模型微调算法。基于类似的思路，MixDA [340]也利用一组域适配器并行注入特定领域的知识，然后训练一个混合适配器门控器，动态融合来自不同域适配器的知识。这种插件式方法在多个领域任务中展示了其可扩展性和效率。同样的方法也被[341,342,343,344]采用，以实现对特定领域或指令数据集的高效微调，并缓解持续学习中出现的灾难性遗忘问题。

 8 加速框架

随着基于Transformer的模型迅速发展，各种模型不断涌现。由于应用场景各异，这些模型在延迟、吞吐量、内存等方面有不同的要求，这使得模型部署变得困难。在本节中，我们将介绍一些最近开发的用于大型语言模型的推理加速框架，这些框架在不同场景下有效地提高了模型的效率，如表6所示。我们根据通用性将这些框架分为通用框架和专用框架。还有一些专门用于训练的加速框架[351,352,353,354,355,356,357]，但由于本文重点关注推理，我们将不具体讨论它们。如果您想快速部署训练好的模型以获得高效推理，可以参考这些框架[358,359,360,361,362,363]。
表6：各种加速框架总结。

 8.1 通用框架

在本节中，我们将介绍一些最近提出的相对通用的框架[345,346]。无论模型部署在何种场景下，我们都可以考虑使用这些框架或结合它们的思路来加速推理，从而获得更高的效率。由于大多数大型模型仍在GPU上部署和运行，这里的通用性是指在GPU硬件下的通用性。

算子融合是一种常见的加速模型推理的方法，它通过消除不必要的中间结果、降低内存需求以及减少不必要的内存输入输出（IO）和内核启动开销，提高了GPU、CPU和寄存器等计算资源的利用率。同时，算子融合是许多先进的深度神经网络（DNN）编译框架（如TensorFlow XLA [364]、TVM [365]、MNN [366]、PyTorch JIT [367]等）的重要优化手段。然而，这些框架对算子融合有严格的要求，例如TVM使用相对固定的调度模板，导致许多潜在的融合机会被错过。DNNFusion [345]通过对算子进行代数简化和合理分类，具有更好的覆盖范围和融合识别能力。此外，它还通过启发式方法消除不必要的算子，进一步提高了算子融合的效率。

最近，微软提出了DeepSpeed Inference [346]，这是一个针对日益多样化的Transformer模型的高效集成推理系统，在以延迟为导向的前沿场景中，它将延迟降低了7.3倍，在以吞吐量为导向的场景中，吞吐量提高了1.5倍以上。它包括以下两个组件：
多GPU推理解决方案：通过GPU内存聚合，在密集和稀疏Transformer模型中最小化延迟并最大化吞吐量。
异构推理解决方案：除了利用GPU内存和计算资源外，还利用CPU和NVMe内存，为不适合聚合GPU内存的大型模型实现高推理吞吐量。

许多策略已被用于最大化训练吞吐量，如张量并行、流水线并行、ZeRo、专家并行等。然而，小批量推理由于并行度不足而存在以下问题：
- 每次处理的数据量较少，这导致需要频繁从高带宽内存（HBM）读取模型权重并调用内核，从而产生显著的开销。
- 每个内核调用将数据写入全局内存，GPU在下一次内核调用时必须重新读取这些数据，从而增加了额外的通信开销。
- 当前的cuBLAS和CUTLASS通用矩阵乘法（GeMM）库并未针对小批量进行优化，内存带宽利用率较低。

另一方面，常规的算子融合只能用于逐元素算子。相比之下，Transformer结构中的算子在不同线程块之间引入了数据依赖，这使得算子融合变得具有挑战性。这是因为如果一个线程块消耗了另一个线程块生成的数据，在GPU上就需要进行全局内存同步才能调用新的内核。为了避免全局同步的需求，Deep - Fusion沿着迭代空间的维度对计算空间进行分块，使得不会出现跨块数据依赖。此外，它为小批量定制设计了GeMM，并使其能够与Deep - Fusion融合，以实现最大的内存带宽利用率。对于小批量，Deep - Fusion在Transformer层中进行四次算子融合，以获得四个定制内核，如图9中红色虚线框所示。对于大批量，算子融合策略相同，区别在于直接使用cuBLAS中的GeMM，而不是定制的GeMM。

图9：小批量推理的Deep - Fusion策略

 8.2 专用框架

在本节中，我们将介绍一些最近提出的专用框架。这些框架是为特定场景和需求定制的，可以根据不同的要求进行调整。如果您在某些方面有较高的需求，可以考虑单独部署这些模型。

与其他场景相比，将Transformer模型高效部署到服务器上需要满足服务的低延迟和高吞吐量要求，这是一个巨大的挑战。此外，由于请求的不可预测性以及自然语言处理任务中使用变长句子的情况，输入维度的可变性给有效的内存管理和服务优化带来了严重问题。TurboTransformer [347]提出了一种序列长度感知的内存分配算法和批调度算法，该算法将最大化响应吞吐量视为一个动态规划问题，实现了可变维度中间张量的高效内存重用和最优批调度方案。TurboTransformer还提出了一种针对高频算子（如Softmax和LayerNorm）的并行近似算法，显著提高了效率。然而，TurboTransformer的主动分组方法仍然会引入不可消除的填充开销。基于此，ByteTransformer [348]提出了一种无填充算法，使整个Transformer摆脱了对零填充token的冗余计算。此外，ByteTransformer针对零填充算法优化了多头注意力，使得注意力不再面临对无用token的冗余计算，进一步提高了性能。

与之前的工作不同，FlexGen [349]几乎完全牺牲了推理计算服务的延迟，以极化设计一个仅专注于吞吐量的大型语言模型计算系统。因此，它仅适用于离线计算。在仅追求吞吐量时，可以重新考虑大型语言模型加速器的各个方面，包括存储管理、跨域内存层次结构中内存访问的延迟隐藏设计以及并行化策略。FlexGen提出了一种基于之字形并行化策略的新的卸载式推理系统，其吞吐量比DeepSpeed Zero - Inference高出40多倍。我们认为这项工作最具启发性的方面在于它强调了发散思维的重要性，强调需要更深入地挖掘问题的细节并探索替代解决方案。

最近，开源推理框架PowerInfer [350]使大型语言模型推理速度提高了11倍。在不进行量化且使用FP16精度的情况下，它允许400亿参数的模型在RTX4090 PC上流畅运行；如果添加量化，2080 Ti也可以流畅运行700亿参数的模型。它基于大型语言模型中高度局部化的稀疏激活，即输入时始终有一小部分神经元（热神经元）被激活，而大多数神经元（冷神经元）根据特定输入做出响应。PowerInfer利用这一特性以及CPU擅长条件计算、GPU擅长简单并行计算的事实，开发了一种创新的GPU - CPU混合推理引擎。这意味着热神经元被预加载到GPU中以实现快速访问，而冷神经元则在CPU上进行计算，从而显著降低了GPU的内存需求以及CPU和GPU之间的数据传输量。此外，PowerInfer集成了自适应预测器和神经元特定的稀疏优化，以提高神经元激活和计算的稀疏效率。总体而言，PowerInfer使PC用户能够在本地运行先进的大型语言模型，而无需昂贵的专用硬件。这为AI应用的普及提供了便利，为爱好者、研究人员和小型企业提供了前所未有的机会。

目前已经有更多针对大型模型多GPU分布式推理的加速器，但针对边缘设备部署的加速器相对较少。随着在边缘设备上部署AI大型模型的需求不断增长，这将成为一个紧迫的问题。

 9 结论

本文从算法角度对大型语言模型的压缩和高效推理进行了全面研究，涵盖了量化、剪枝、知识蒸馏、紧凑架构设计和动态网络等方面。此外，我们还介绍了一些针对大型语言模型的流行压缩和加速框架。然而，正如我们在引言中提到的，与小型模型相比，大型模型的压缩和加速面临更多挑战。尽管现有算法已在应对这些挑战方面做出了巨大努力，但许多算法仍然依赖为压缩小型模型而设计的框架，压缩大型模型的挑战依然存在。未来，需要进一步探索开发更高效、有效的压缩算法，同时确保大型模型的通用性和泛化能力。