卷积到底是如何操作的？1x1卷积？参数如何计算？

目录

卷积到底是如何操作的

filter的参数如何计算

卷积的特性

1x1的卷积核

---

---

卷积到底是如何操作的

• 1. 对于一个特征图（如灰度图）             

 

卷积就是对应元素乘积的求和,然后在加上一个非线性函数。

但是上面的例子只有一个输入channel和一个卷积核，当有很多channel和多个卷积核时，又改如何计算呢？

---

• 2. 多个特征图如何和多个filter进行运算呢？

先来看动图，这里有三个输入维度，两个卷积核，最后输出的是两个特征图。

Remember：一个filter就是一个特征，一般会有多个卷积核（也就是多个channel），所以，一个filter更多的时候是一个长方体，而不是一个平面，为什么会这样呢？

因为，并不是每个特征图和每个卷积核去匹配的，而是所有的输入channel同时和一个filter做运算，也就是多个卷积核的对应元素乘积的求和。因此对于一个filter，它应该具有和原图相同的channel 。如原图是3通道的，那么filter也应该是3通道 ​。当然filter的channel的参数不需要人为设置，因为它就是输入层的channel数，但计算时需要考虑。

 

• 单个filter  -- 含有多个特征图（可看做彩色图片的三个通道）

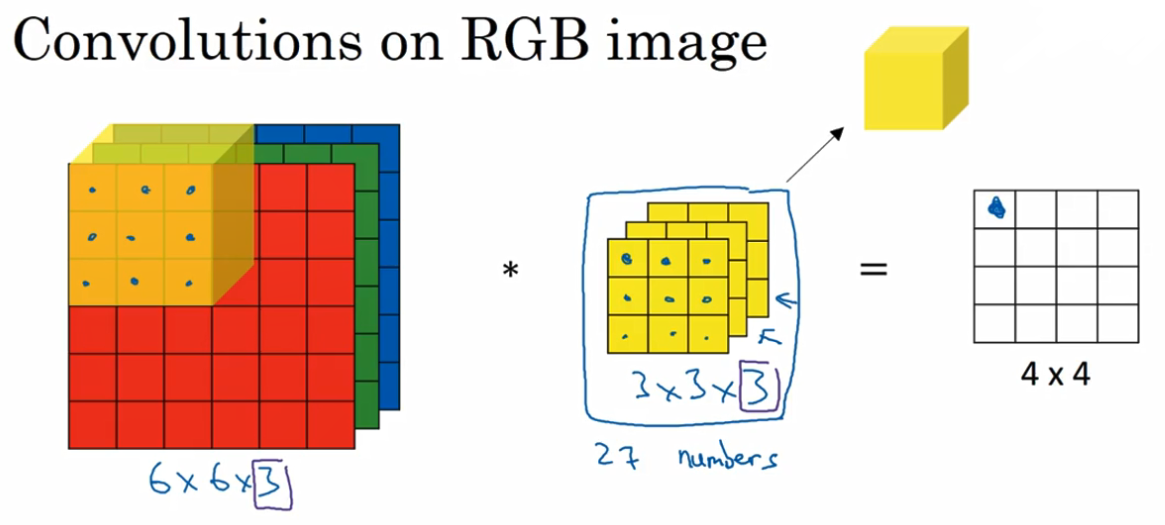
上图看起来有三个filter，其实就是一个一个含有三个channel的filter

• 多个filter

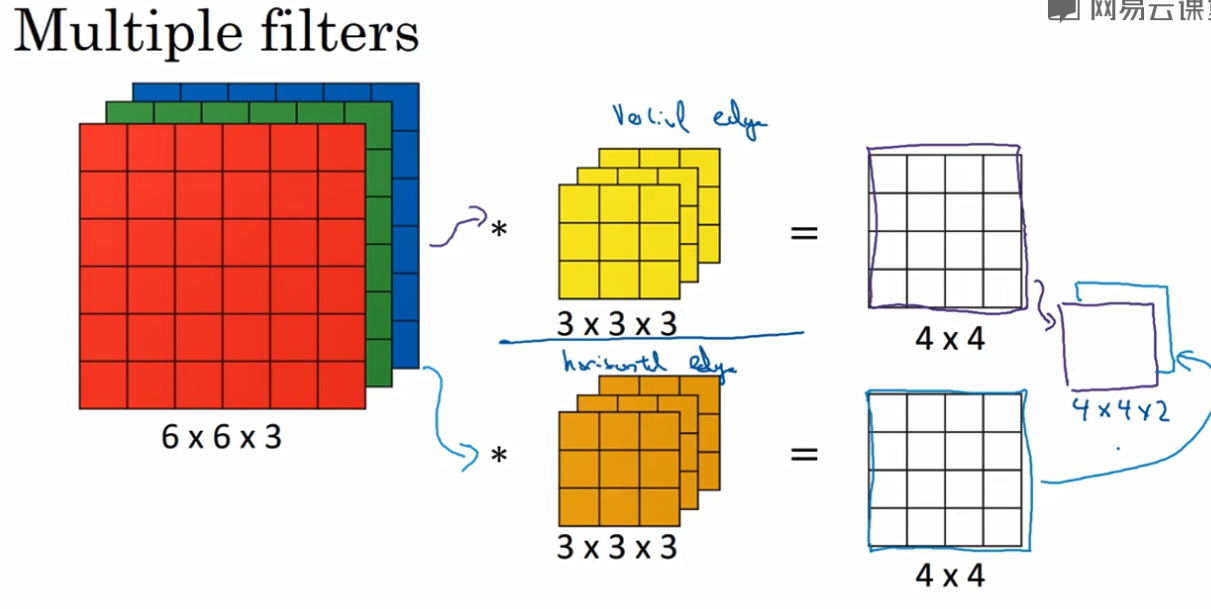
上图中有两个 filter，也就是两个特征，每个含有三个channel，所以最后会输出两个特征图。

 

---

filter的参数如何计算

 

以VGG16的 block1_conv1为例，卷积核是3x3(大家肯定都知道），filter的个数是64，也就是说会输出64个特征图。filter的输入维度是3，因此参数的个数应该是    (3x3x3+1)x64 = 1792

前面3x3表示一个channel的参数数目，后面的3指的是输入层的channel，加1表示每个filter含有偏置

 

再举个例子：请看block2_conv1 它的参数应该是（3x3x64+1）x128 = 73856

In [2]:
from keras.applications.vgg16 import VGG16

In [4]:
model = VGG16()
In [5]:

model.summary()
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
input_1 (InputLayer)         (None, 224, 224, 3)       0         
_________________________________________________________________
block1_conv1 (Conv2D)        (None, 224, 224, 64)      1792      
_________________________________________________________________
block1_conv2 (Conv2D)        (None, 224, 224, 64)      36928     
_________________________________________________________________
block1_pool (MaxPooling2D)   (None, 112, 112, 64)      0         
_________________________________________________________________
block2_conv1 (Conv2D)        (None, 112, 112, 128)     73856     
_________________________________________________________________
block2_conv2 (Conv2D)        (None, 112, 112, 128)     147584    
_________________________________________________________________
block2_pool (MaxPooling2D)   (None, 56, 56, 128)       0         
_________________________________________________________________
block3_conv1 (Conv2D)        (None, 56, 56, 256)       295168    
_________________________________________________________________
block3_conv2 (Conv2D)        (None, 56, 56, 256)       590080    
_________________________________________________________________
block3_conv3 (Conv2D)        (None, 56, 56, 256)       590080    
_________________________________________________________________
block3_pool (MaxPooling2D)   (None, 28, 28, 256)       0         
_________________________________________________________________
block4_conv1 (Conv2D)        (None, 28, 28, 512)       1180160   
_________________________________________________________________
block4_conv2 (Conv2D)        (None, 28, 28, 512)       2359808   
_________________________________________________________________
block4_conv3 (Conv2D)        (None, 28, 28, 512)       2359808   
_________________________________________________________________
block4_pool (MaxPooling2D)   (None, 14, 14, 512)       0         
_________________________________________________________________
block5_conv1 (Conv2D)        (None, 14, 14, 512)       2359808   
_________________________________________________________________
block5_conv2 (Conv2D)        (None, 14, 14, 512)       2359808   
_________________________________________________________________
block5_conv3 (Conv2D)        (None, 14, 14, 512)       2359808   
_________________________________________________________________
block5_pool (MaxPooling2D)   (None, 7, 7, 512)         0         
_________________________________________________________________
flatten (Flatten)            (None, 25088)             0         
_________________________________________________________________
fc1 (Dense)                  (None, 4096)              102764544 
_________________________________________________________________
fc2 (Dense)                  (None, 4096)              16781312  
_________________________________________________________________
predictions (Dense)          (None, 1000)              4097000   
=================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0
_________________________________________________________________

​

• 卷积的特性

• 1. 卷积的参数为甚这么少

  • 权值共享
    因为一个特征检测如垂直边缘检测，如果适用于图片的某个区域，一定也适用于其他区域

  • 稀疏连接
    对于每个layer,它的输出值之和很少的输入数据有关，如红色圆圈的数值之和原图中的3x3的大小的数据有关。

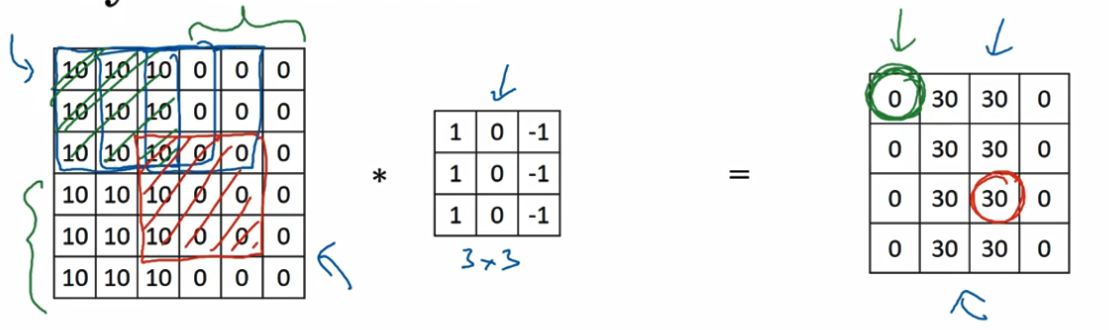
• 2.为啥具有平移不变性

     由于卷积的结构，即使移动几个像素值，仍然具有相似的特征。

---

 

1x1的卷积核

这是最简单的1x1卷积，这时候输出channel是filter的channel都是1，这时候只是乘以一个倍数，显然没什么作用，继续看

现在输出channel是32，此时才能发挥它的作用。

上文说过，filter的channel必须和输入的channel相等，因此，这个1x1的filter 的channel也是32

操作：这个黄色的1x1的filter，先与蓝色长方体的左上角的一个1x1x32的长方体，对应元素相乘，求和，然后在加一个非线性运算，如Relu,就得了右图的一个数据点。然后依次遍历所有的位置，就生成了一张6x6的特征图。

这只是一个filter，当有n的1x1的filter时，就会有n个特征图。

因此，有没有发现，1x1的卷积核，并不改变图像的高宽，但可以改变模型的维度。因此也可以用于模型压缩，继续往后看。

• 1x1的卷积如何实现模型压缩？

举个栗子：我们希望实现，从28x28x192 到28x28x32的转换

如果用5x5卷积的话，通过padding可以实现图片尺寸不变

此时的参数个数为：（5x5x32 + 1）x 192 = 153792

但是如果，你在中间加上一层1x1的卷积，先把输入的维度，降下来，在用5x5的卷积时，参数个数会怎么样呢？

参数：(1x1x16+ 1)x192 + (5x5x32 + 1)x16 = 16080，仅仅是原来的十分之一，特别当维度很高时，参数的减少越明显。

中间的这层，也被称为瓶颈层，bottleneck layer。

大家可能会问，把维度参数降低了这么多，维度也从192到了16，网络结构性能不会下降吗？

既然现在1x1的卷积被广泛的应用，也就说明只要合理构建bottleneck layer ,既可以减少参数，运算量，也不会降低网络性能​​

1x1的卷积的典型应用，请去看inception系列的网络结构。建议去看吴恩达 Andrew Ng的网易云课程。