关于高维空间的一些思考

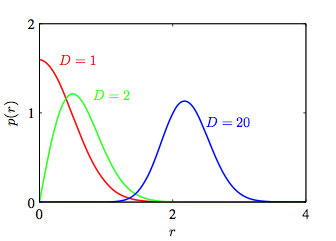
首先，我们来做一个思想实验，网格世界中随机游走的小球（作出每种移动的可能性相同）。首先是1维的随机游走，最后的结果一定是高斯分布（因为那就是一个伯努力过程），结果就是，我们在原点附近发现小球的概率一定很大；现在来看二维的情况，现在有4个方向可以选择，所以这是一个二维高斯（而且考虑到正交方向的独立性，协方差矩阵为单位矩阵），那么我们现在问在距离原点多远的地方发现小球的概率比较大？经过简单的换元法（注意别忘了乘以雅可比行列式），我们会惊讶的发现，小球出现在原点附近的概率几乎是0，而出现在距离原点1到2之间的地方的概率非常大。一个随机游走的小球居然在维度升高以后远离了最初的原点，这不是很不可思议吗？我们该如何句理解这个现象呢？如果我们进一步提高空间的维度，发现小球的位置会距离原点越来越远，虽然我们一开始确实是从原点开始的。

也许这个现象有数学之外更哲学的解释。事实上，问题不是出在高斯函数自身上，而是所有的高维对象——这是空间本身的问题！当计算一个球体的体积时会发现随着空间维度升高，球体的体积越来越集中在一个很薄的球壳区域。因此，数学上来说，高维度空间中的空间分布是不均匀的。现在，从哲学上来思考，如果我们说某个实体存在，它必须存在于空间中，不存在于空间中的实体被认为是不存在的，不是吗？所以在某些地方你看不到目标，不是因为目标不去那个地方，而是因为那个地方几乎就没有空间！

现在想象一下这个情形，一个随机移动的点，无论怎么疯狂的移动，却总是被限定在一个球壳区域中，以至于它的运动轨迹甚至形成一个球壳，而原点正好处于球心处......如果说，我在现实中真的见过什么现象是这样的，那我唯一能想到的那就是氢原子！

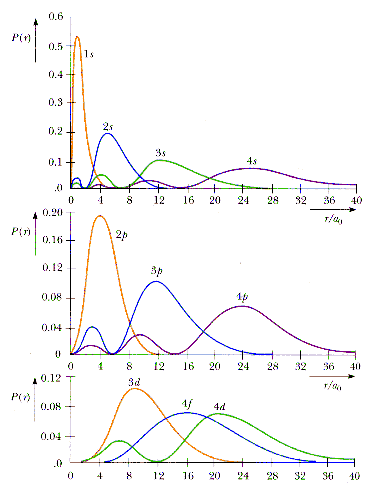
事实上我第一时间想到这种关联性以后，就去查了原子核核外电子的分布函数图：

注意观察那些函数的形状，虽然它们有形态上的差异，但是实际上它们就是高斯函数！（换元以后的）：

现在，一个非常疯狂的猜想在我脑中闪现：原子核附近如果存在高维空间呢？！如果原子核附近确实存在高维空间，那么就可以解释电子云为什么是这样的，为什么原子有大小，为什么原子中99%的空间是空的（因为空间根本就不存在！）。传统的说，原子核本来就存在于三维空间中，所以出现这种概率分布也是没什么非议的。不！问题的关键在于，为什么电子有多个轨道（分布）？！而且这些轨道（分布）都是互相独立开来的，这不很奇怪吗？这也是量子理论最奇特的地方——量化的能量、量化的轨道、量化的分布。之始至终，我们的世界就是连续的，我们的一切分析与认知也是基于连续的，我们在研究一个连续统的过程中，突然跳出了不连续的特性。很早以前，我们以为自己解决了Zeno悖论，为什么无限个静止的瞬间无法组成一个连续的世界？那是因为即使你有无限个静止的瞬间，你依然无法构成一个连续统，这就是数学或者哲学的认知——但是现在这个认知受到了挑战。问题出在哪？

在所有的分析过程中，我们都是用的连续量，唯一不连续的、唯一只能取整数值的只有维度——空间的维度是不连续的！不连续性难道不是由于空间维度的不连续性造成的吗？也许，我们需要一种新的理论，把能量和空间维度结合起来考虑，更高的能量使得能利用的维度越高？？

I gotta stop somewhere, I'll leave you something to image...