《UnityShader入门精要》数学部分 名词 与 公式记录

本文为我读《UnityShader入门精要》(冯乐乐著)的笔记
书中使用的unity版本是5.2.1

4.2.2正交基

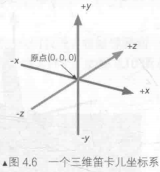
三个坐标轴被称为该坐标的 基矢量
三轴之间相互垂直，且长度为1，可被成为 标准正交基。相互垂直但长度不为1被称为 正交基。

4.3.2矢量运算

标量与矢量乘除法：

$$【v表示一个矢量】【k表示一个标量】kv=(k{v}_x,k{v}_y,k{v}_z)$$
矢量除以非零的标量，等于乘以这个标量的倒数
$$\frac{v}{k}=\frac{(x,y,z)}{k}=\frac{1}{k}=\left(\frac{x}{k},\frac{y}{k},\frac{z}{k}\right),k\ne 0$$

标量与矢量加减法：

$$a\pm b=(a_x\pm b_x,a_y\pm b_y,a_z\pm b_z)$$

矢量的模:

$$|v|=\sqrt{v_x^2,v_y^2,v_z^2}$$

单位矢量:

即模为1的矢量，也被称为被归一化的矢量
对任何非零矢量，将其转化为单位矢量的过程被称为归一化
$$\text{aˆ}=\frac{v}{|v|},v是非零矢量(0,0,0)$$

矢量的点积：

先复习一下三角函数:

	$$0^{\circ }$$	$$15^{\circ }$$	$$30^{\circ }$$	$$45^{\circ }$$	$$60^{\circ }$$	$$90^{\circ }$$	$$120^{\circ }$$	$$135^{\circ }$$	$$150^{\circ }$$	$$180^{\circ }$$	$$270^{\circ }$$
弧度	$$0$$	$$\frac{\pi }{12}$$	$$\frac{\pi }{6}$$	$$\frac{\pi }{4}$$	$$\frac{\pi }{3}$$	$$\frac{\pi }{2}$$	$$\frac{2\pi }{3}$$	$$\frac{3\pi }{4}$$	$$\frac{5\pi }{6}$$	$$\pi$$	$$\frac{3\pi }{2}$$
$$正弦(对比斜)\sin \alpha$$	$$0$$	$$\frac{\sqrt{6}-\sqrt{2}}{4}$$	$$\frac{1}{2}$$	$$\frac{\sqrt{2}}{2}$$	$$\frac{\sqrt{3}}{2}$$	$$1$$	$$\frac{\sqrt{3}}{2}$$	$$\frac{\sqrt{2}}{2}$$	$$\frac{1}{2}$$	$$0$$	$$-1$$
$$余弦(邻比斜)\cos \alpha$$	$$1$$	$$\frac{\sqrt{6}+\sqrt{2}}{4}$$	$$\frac{\sqrt{3}}{2}$$	$$\frac{\sqrt{2}}{2}$$	$$\frac{1}{2}$$	$$0$$	$$-\frac{1}{2}$$	$$-\frac{\sqrt{2}}{2}$$	$$-\frac{\sqrt{3}}{2}$$	$$-1$$	$$0$$
$$正切(对比邻)\tan \alpha$$	$$0$$	$$2-\sqrt{3}$$	$$\frac{\sqrt{3}}{3}$$	$$1$$	$$\sqrt{3}$$	$$\varnothing$$	$$-\sqrt{3}$$	$$-1$$	$$-\frac{\sqrt{3}}{3}$$	$$0$$	$$\varnothing$$
$$余切(邻比对)\cot \alpha$$	$$\varnothing$$	$$2+\sqrt{3}$$	$$\sqrt{3}$$	$$1$$	$$\frac{\sqrt{3}}{3}$$	$$0$$	$$-\frac{\sqrt{3}}{3}$$	$$-1$$	$$-\sqrt{3}$$	$$\varnothing$$	$$0$$

点积的结果是一个标量，当两矢量夹角<90°时，点积结果为正；=90°时，结果为0；>90°是结果为负。
点积的几何意义就是投影(视频1:30处)
$$a\cdot b=(a_x,a_y,a_z)\cdot (b_x,b_y,b_z)=a_x{b}_x+a_y{b}_y+a_z{b}_z$$
$$a\cdot b=|a||b|\cos \theta$$
$$点乘满足交换律：a\cdot b=b\cdot a$$
其还存在以下性质：
$$(ka)\cdot b=a\cdot (kb)=k(a\cdot b)$$
$$a\cdot (b\pm c)=a\cdot b\pm a\cdot c$$
$$矢量与自己的点积=该矢量模的平方即：v\cdot v=v_x{v}_x+v_y{v}_y+v_z{v}_z=|v{|}^2$$

矢量的差积：

叉积也成外积，矢量叉积的结果是一个矢量(5:30处)，该矢量同时垂直于叉积的两个矢量，该矢量的模为两矢量构成的平行四边形的面积
$$a\times b=(a_x,a_y,a_z)\times (b_x,b_y,b_z)=(a_y{b}_z-a_z{b}_y,a_z{b}_x-a_x{b}_z,a_x{b}_y-a_y{b}_x)$$
$$|a\times b|=|a||b|\sin \theta$$

$$叉乘满足反交换律，不满足交换律：a\times b=-(b\times a)\ne b\times a$$

$$叉乘不满足结合律：(a\times b)\times c\ne a\times (b\times c)$$

4.4.3矩阵与矩阵运算

矢量可以视作：列矩阵(n行×1列的矩阵) 或 行矩阵(1行×n列的矩阵)

$$一个\underset{˜}{标量K}与\underset{˜}{矩阵M}相乘：KM=MK=K\left[\begin{array}{ccc}{m}_{11}& m_{21}& m_{31}\\ m_{12}& m_{22}& m_{32}\\ m_{13}& m_{23}& m_{33}\end{array}\right]=\left[\begin{array}{ccc}k{m}_{11}& k{m}_{21}& k{m}_{31}\\ k{m}_{12}& k{m}_{22}& k{m}_{32}\\ k{m}_{13}& k{m}_{23}& k{m}_{33}\end{array}\right]$$
矩阵与矩阵相乘:对应元素值如下所示：$$例如：c_{11}=a_{11}{b}_{11}+a_{21}{b}_{12}$$

矩阵与矩阵相乘:	$$\left[\begin{array}{ccc}{b}_{11}& b_{21}& b_{31}\\ b_{12}& b_{22}& b_{32}\end{array}\right]$$
$$\left[\begin{array}{cc}{a}_{11}& a_{21}\\ a_{12}& a_{22}\end{array}\right]$$	$$\left[\begin{array}{ccc}{c}_{11}& b_{21}& c_{31}\\ c_{12}& c_{22}& c_{32}\end{array}\right]$$

性质：
$$不满足交换律：AB\ne BA$$
$$满足结合律：(AB)C=A(BC)由此可得：ABCDE=((A(BC))D)E=(AB)(CD)E$$

特殊矩阵：

1.方块矩阵(方阵)
行数与列数相等的矩阵，也就是1×1,2×2,3×3,…n×n的矩阵
对角矩阵： 除了对角元素的其他所有元素都为0的方块矩阵
$$例如：=\left[\begin{array}{cccc}n& 0& 0& 0\\ 0& m& 0& 0\\ 0& 0& x& 0\\ 0& 0& 0& y\end{array}\right]$$
2.单位矩阵
单位矩阵是对角元素全为1的对角矩阵
$$例如：本书中单位矩阵写为：I=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
$$一个矩阵与单位矩阵相乘等于原矩阵：IM=MI=M$$
3.转置矩阵
$$将一个n\times m的矩阵M翻转为m\times n的矩阵M^T，得到的矩阵就是原矩阵的转置矩阵$$
$$例如：={\left[\begin{array}{cc}m1& n1\\ m2& n2\\ m3& n3\end{array}\right]}^T=\left[\begin{array}{ccc}m1& m2& m3\\ n1& n2& n3\end{array}\right]$$
性质：
1.转置矩阵的转置 等于 原矩阵
$$(M^T{)}^T=M$$
2.矩阵相乘的转置等于各个矩阵的转置矩阵反向相乘
$$（AB{）}^T=B^T{A}^T$$
4.逆矩阵
不是所有矩阵都有逆矩阵，但有逆矩阵的矩阵一定是一个方阵。一个矩阵有对应的逆矩阵则说他是可逆的或者说是非奇异的，反之则说是不可逆的，奇异的
逆矩阵的符号表示为：
$$M的逆矩阵为M^{-1}$$
一个矩阵与他的逆矩阵相乘结果为单位矩阵：
$$M{M}^{-1}=M^{-1}M=I$$
性质：
1.逆矩阵的逆矩阵是原矩阵本身
$$(M^{-1}{)}^{-1}=M$$
2.单位矩阵的逆矩阵是它本身
$$I^{-1}=I$$
3.转置矩阵的逆矩阵是 原矩阵 的逆矩阵的转置
$$(M^T{)}^{-1}=(M^{-1}{)}^T$$
4.逆矩阵相乘后的逆矩阵等于他们的逆矩阵反向相乘
$$(AB{)}^{-1}=B^{-1}{A}^{-1}$$
5.正交矩阵
如果一个方阵与它的转置矩阵的乘积是单位矩阵的话，我们就说这个矩阵是正交的
$$M{M}^T=M^{T}M=I$$
由此可得：如果一个矩阵是正交的，那么他的转置矩阵=逆矩阵
$$M是正交矩阵则：M^T=M^{-1}$$
这个性质非常重要，三维变换会常用到逆矩阵来得到反向变换。但逆矩阵的求解计算量会比较大，如果他是一个正交矩阵矩阵则会好办许多。如何简单的判断一个矩阵是不是正交矩阵需要了解正交矩阵的几何意义(3:50处)。
结论：(将每行的三个元素看做一个矢量)三个矢量都是单位矢量，且三个矢量相互垂直(标准正正交基)。

4.4.5矢量变矩阵的用法

我们可以随意将一个矢量变为行矩阵或列矩阵，但当我们将其与另一个矩阵相乘时会有区别。在unity中常规做法是吧矢量放在矩阵右侧，将矢量变为列矩阵进行计算。

4.5.1变换

变换名称	线性变换	仿射变换	可逆矩阵	正交矩阵
平移矩阵	×	√	√	×
绕坐标轴旋转的旋转矩阵	√	√	√	√
绕任意轴旋转的旋转矩阵	√	√	√	√
绕坐标轴旋转的缩放矩阵	√	√	√	×
错切矩阵	√	√	√	×
镜像矩阵	√	√	√	√
正交投影矩阵	√	√	×	×
透视投影矩阵	×	×	×	×

仿射变换合并线性变换和平移变换的变换类型。仿射变换可以用一个4×4的矩阵表示，为此，我们需要将矢量扩展为4维空间下，这就是齐次坐标空间。

4.5.2齐次坐标

齐次坐标是一个四维矢量(书中泛指四维齐次坐标)。一个三维坐标从三维坐标变为其次坐标：将其第四维w设为1。一个方向矢量，则将w设为0。

4.5.4平移矩阵

对一个点进行平移变换：将点(x,y,z)在空间中平移(tx,ty,tz)个单位
$$\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}x+t_x\\ y+t_y\\ z+t_z\\ 1\end{array}\right]$$
对一个方向矢量进行平移变换，不会发生影响：
$$\left[\begin{array}{cccc}1& 0& 0& t_x\\ 0& 1& 0& t_y\\ 0& 0& 1& t_z\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 0\end{array}\right]=\left[\begin{array}{c}x\\ y\\ z\\ 0\end{array}\right]$$
平移矩阵的逆矩阵：反向平移的矩阵
$$\left[\begin{array}{cccc}1& 0& 0& -t_x\\ 0& 1& 0& -t_y\\ 0& 0& 1& -t_z\\ 0& 0& 0& 1\end{array}\right]$$

4.5.5缩放矩阵

$$对于点\left[\begin{array}{cccc}{k}_x& 0& 0& 0\\ 0& k_y& 0& 0\\ 0& 0& k_z& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}{k}_{x}x\\ k_{y}y\\ k_{z}z\\ 1\end{array}\right]$$
$$对于向量\left[\begin{array}{cccc}{k}_x& 0& 0& 0\\ 0& k_y& 0& 0\\ 0& 0& k_z& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 0\end{array}\right]=\left[\begin{array}{c}{k}_{x}x\\ k_{y}y\\ k_{z}z\\ 0\end{array}\right]$$
如果kx=ky=kz则称为统一缩放，否则为非统一缩放。
缩放矩阵的逆矩阵是原来缩放系数的倒数进行缩放。
$$\left[\begin{array}{cccc}\frac{1}{k_x}& 0& 0& 0\\ 0& \frac{1}{k_y}& 0& 0\\ 0& 0& \frac{1}{k_z}& 0\\ 0& 0& 0& 1\end{array}\right]$$

4.5.6旋转矩阵

绕x轴旋转：
$$R_x(\theta )=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$$
绕y轴旋转：
$$R_y(\theta )=\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$$
绕z轴旋转：
$$R_z(\theta )=\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin \theta & \cos \theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]$$

4.5.7复合变换

绝大多数情况下，我们约定变换顺序是先缩放，再旋转，最后平移
$$v_{new}=M_{平移}{M}_{旋转}{M}_{缩放}{v}_{old}$$
关于旋转顺序：unity中旋转顺序是zxy，即：先绕z轴旋转，再绕x轴旋转，最后绕y轴旋转
$$M_{rotatZ}{M}_{rotatX}{M}_{rotatY}=\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin \theta & \cos \theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& \cos \theta & -\sin \theta & 0\\ 0& \sin \theta & \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}\cos \theta & 0& \sin \theta & 0\\ 0& 1& 0& 0\\ -\sin \theta & 0& \cos \theta & 0\\ 0& 0& 0& 1\end{array}\right]$$

4.6.2坐标空间的变换

设：父坐标空间P和子坐标空间C 我们常用到将C下的点与矢量转换到P下 或 相反：Mc->p,Mp->c
如果我们得到Mc->p，其逆矩阵便是Mp->c
而求Mc->p时，我们知道C的三个坐标轴在P下表示为xc,yc,zc,以及其原点位置Oc
那么我们可以得到他的变换矩阵为：
$$M_{c\to p}=\left[\begin{array}{cccc}|& |& |& |\\ x_c& y_c& z_c& O_c\\ |& |& |& |\\ 0& 0& 0& 1\end{array}\right]$$
对方向矢量的坐标空间变幻可以使用3×3的矩阵表示，不需要表示平移变换。
$$M_{c\to p}=\left[\begin{array}{cccc}|& |& |& \\ x_c& y_c& z_c& \\ |& |& |& \end{array}\right]$$
模型空间：也叫对象/局部空间，模型自己独有的坐标空间。
世界空间：宏观概念上的最大空间。
观察空间：摄像机空间。
裁剪空间：（齐次裁剪空间）由视锥体来决定对渲染图源进行裁剪的空间。完全位于这块空间内部的图元将会被保留，完全位于这块空间外部的图元将会被剔除，而与这块空间边界相交的图元就会被裁剪。视椎体有两种：正交投影与透视投影。
屏幕空间：像素位置投影的二维空间。

模型变换：将顶点坐标从模型空间变换到世界空间中。
观察变换：将顶点坐标从世界空间变换到观察空间中。
投影变换：从观察空间到裁剪空间，其中用于变换的矩阵叫裁剪矩阵（投影矩阵）。
Aspect：摄像机纵横比。FOV：摄像机可视角度。Near：近裁剪平面距离。Far：远裁剪平面距离。
透视投影矩阵与顶点相乘后结果本质是对xyz分量做了不同程度的缩放(z有了平移)，此时w分量不再是1：
$$M_{透视投影矩阵}{P}_{顶点}\left[\begin{array}{cccc}\frac{\cos \frac{FOV}{2}}{Aspect}& 0& 0& 0\\ 0& \cos \frac{FOV}{2}& 0& 0\\ 0& 0& -\frac{Far+Near}{Far-Near}& -\frac{2\cdot Far\cdot Near}{Far-Near}\\ 0& 0& -1& 0\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}x\frac{\cos \frac{FOV}{2}}{Aspect}\\ y\cos \frac{FOV}{2}\\ -z\frac{Far+Near}{Far-Near}-\frac{2\cdot Far\cdot Near}{Far-Near}\\ -z\end{array}\right]$$
Size:视椎体垂直方向上高度的一半。
正交投影矩阵与顶点相乘后：
$$M_{正交投影矩阵}{P}_{顶点}\left[\begin{array}{cccc}\frac{1}{Aspect\cdot Size}& 0& 0& 0\\ 0& \frac{1}{Size}& 0& 0\\ 0& 0& -\frac{2}{Far-Near}& -\frac{Far+Near}{Far-Near}\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{c}\frac{x}{Aspect\cdot Size}\\ \frac{y}{Size}\\ -\frac{2z}{Far-Near}-\frac{Far+Near}{Far-Near}\\ 1\end{array}\right]$$
现在判断顶点在不在视椎体内，它需要满足-w≤x≤w,-w≤y≤w,-w≤z≤w
齐次除法与屏幕映射：齐次除法也叫透视除法，用w分量去除以x,y,z分量。得到归一化的设备坐标(NDC)。
unity中屏幕空间左下角的像素坐标是(0,0)。
齐次除法与屏幕映射的过程（unity会帮我们完成）：
pixelWidth与pixelHeight是当前的屏幕像素宽高。cilpx/y是裁剪空间中的坐标x与y。
$$scree{n}_x=\frac{cli{p}_x\cdot pixelWidth}{2\cdot cli{p}_x}+\frac{pixelWidth}{2}$$
$$scree{n}_y=\frac{cli{p}_y\cdot pixelHeight}{2\cdot cli{p}_y}+\frac{pixelHeight}{2}$$

4.8UnityShader内置变量

4.8.1变换矩阵

Unity内置的变换矩阵	描述
UNITY_MATRIX_MVP(后来版本变更为UnityObjectToClipPos())	当前模型·观察·投影矩阵，将顶点/方向矢量 从模型空间变换到裁剪空间
UNITY_MATRIX_MV	当前模型·观察矩阵，将顶点/方向矢量 从模型空间变换到观察空间
UNITY_MATRIX_V	当前观察矩阵，将顶点/方向矢量 从世界空间变换到观察空间
UNITY_MATRIX_P	当前投影矩阵，将顶点/方向矢量 从观察空间变换到裁剪空间
UNITY_MATRIX_VP	当前观察·投影矩阵，将顶点/方向矢量 从世界空间变换到裁剪空间
UNITY_MATRIX_T_MV	UNITY_MATRIX_MV 的转置
UNITY_MATRIX_IT_MV	UNITY_MATRIX_MV 的逆转置，用于将法线从模型空间变换到观察空间，也可用于得到UNITY_MATRIX_MV 的逆矩阵
_Object2World	当前的模型矩阵，用于将顶点/方向矢量从模型空间变换到世界空间
_World2Object	_Object2World的逆矩阵，用于将顶点/方向矢量从世界空间变换到模型空间

4.8.2摄像机和屏幕参数

变量名	类型	描述
_WorldSpaceCameraPos	float3	该摄像机在世界空间中的位置
_ProjectionParams	float4	x=1.0(或-1.0，如果正在使用一个翻转的投影矩阵进行渲染)，y=Near，z=Far，w=1.0+1.0/Far，其中Far和Near分别是近裁剪平面和远裁剪平面的摄像机距离
_ScreenParams	float4	x=width,y=height,z=1.0+1.0/width,w=1.0+1.0/height，其中width和height分别是该摄像机的渲染目标的像素宽度和高度
_ZBbufferParams	float4	x=11-Far/Near,y=Far/Near,z=x/Far,w=y/Far,该变量用于线性化Z缓存中的深度值
unity_OrthoParams	float4	x-width,y=height,z没有定义,w=1.0（正交摄像机）或w=0.0（透视摄像机），其中width和height是正交投影摄像机的宽度和高度
unity_CameraProjection	float4×4	该摄像机的投影矩阵
unity_CameraInvProjection	float4×4	该摄像机的投影矩阵的逆矩阵
unity_CameraWorldClipPlanes[6]	float4	该摄像机的6个裁剪平面在世界空间下的等式，按如下顺序：左，右，下，上，近，远 裁剪平面