统计学基础性概念有关笔记

第1章 绪论

第一节 无处不在的统计学

一、统计的含义

• 统计工作（又称统计实践）是搜集、整理、分析和提供关于社会经济现象的数字资料工作的总称。
• 统计资料即统计数据，是统计实践活动过程所获得的各种数字资料及其他资料的总称，是统计实践活动的的成果。
• 统计学是研究如何收集、整理、分析反映客观现象总体数量的数据，以便给出正确认识的方法论科学。

二、统计学的产生和发展

1. 古典统计学时期

   政治算术学派

   国势学派

2. 近代统计学时期

   社会统计学派

   数理统计学派

3. 现代统计学

   理论统计学

   应用统计学

三、无处不在的统计学

一个学科如果连定量都做不到一定是不成熟的。生物、医学、经济、金融、国防等社会生活的各个方面都需要数学来量化，任何一个体系运行的好坏都要通过数据来检验，现代科技的发展更是把改进技术指标的关键变成了统计问题。—— 范剑青

应用案例：

• 制定宏观经济政策
• 产品质量管理
• 抽样调查
• 红楼梦电视剧分析
• 军事应用

统计学是用数据的方式给大家讲故事，使我们了解身边正在发生了什么，事物间的关系，帮助我们解决存在的问题。

统计使人豁达，见怪不怪！

第二节 统计学的研究对象和分类

一、统计学研究对象

自然现象和社会经济现象的数量方面

二、统计学分类

• （一）描述统计和推断统计
  1. 描述统计学
  2. 推断统计学（核心内容）
• （二）理论统计和应用统计
  1. 理论统计学
  2. 应用统计学

三、统计学基本内容

第三节 统计学的语言

1. 总体、总体单位、样本

   统计总体和单位是相对的

2. 同质、变异

   同质：相同的背景、条件、属性等。

   变异：同质事物个体间的差异。 变异是统计学存在的基础。

3. 标志、标志表现、变量

   标志：说明总体单位的属性和特征的名称。

   品质标志：标志表现形式为文字

   数量标志：标志表现为数字

   标志表现（也叫标志值）：标志名称之后所表明的具体属性和数值。

   变量：可变的数量标志。

4. 统计指标

   综合反映总体数量特征的概念和数值。

   数量指标 绝对数

   质量指标 相对数和平均数

   统计指标与标志既有区别又有联系。 主要区别在于：统计指标是说明总体特征的，而标志是说明总体单位特征的。统计指标分为数量指标和质量指标，它们都可以用数量来表示；而标志分为数量标志和品质标志，数量标志可以用数量来表示，但品质标志只能用文字表示。 二者的密切联系：有许多指标的数值是从总体单位数量标志的标志值汇总而来的。

5. 统计指标体系
   是由一系列相互联系的统计指标所组成的有机整体。用以反映所研究现象各方面相互依存相互制约的关系。

---

第2章 统计调查

第一节 统计调查概述

一、统计调查的含义

按照统计任务的要求，运用科学的调查方法，有组织地搜集统计资料的工作过程。
统计调查决定了整个统计工作的质量。

二、统计调查的基本要求

• 全面性
• 准确性
• 及时性
• 方便性

三、统计调查的种类

按调查对象的范围分：

• 全面调查：如人口普查
• 非全面调查：如月饼质量、电视收视率调查

按调查时间的连续性分为：

• 经常调查：客流量调查、资金流调查
• 一次性调查 ：人口普查

按组织形式分为：

• 统计报表：统计公报
• 专门调查：普查、重点调查等

第二节 统计调查方案

1. 确定调查的目的

2. 确定调查对象、调查单位和报告单位

   调查对象是根据调查目的确定的调查研究总体。

   调查单位是构成调查对象的每一个单位

3. 确定调查项目

4. 拟订调查表

   把调查项目按一定的顺序排列在一定的表格，就构成了调查表

5. 确定调查时间和调查期限

   调查时间是指调查资料所属的时间；

   调查期限是指调查工作的起讫时间。

6. 制定调查的组织实施计划

第三节 调查组织方式

一、普查

是国家为详尽了解某项重要的国情国力而专门组织的一次性全面调查。

特点：

一次性

全面性

资料准

费用高

普查原则：

1. 选择最适宜的标准时点和期限。

2. 登记工作在普查范围同时进行。

3. 普查项目统一规定。

4. 同类普查的项目要前后保持一致，建立周期性的普查制度。

二、重点调查

重点单位:这些单位的单位数在总体中占的比重很小，而标志总量占的比重很大。

特点：

非全面性，可较快地了解总体的基本资料。

重点单位易确定。

重点单位的选择原则：

根据调查目的和任务。

对确定的重点单位进行小范围的全面调查。

三、典型调查

先对总体进行分析，然后选择有代表性的单位进行非全面调查。

特点：

能取得详细的资料。

能取得代表性较高的资料。

调查方式灵活。

典型单位的选择：

总结经验：先进典型

汲取教训：落后典型

探索事物发展的一般规律或了解一般情况：中间典型

四、抽样调查

特点：

1. 按随机原则抽选样本
2. 目的在于推断总体特征
3. 抽样误差可以计算和控制

几种抽样调查的形式：

• 简单随机抽样
• 分层抽样
• 整群抽样
• 等距抽样

抽样、重点、典型调查区别：

（1）样本选取不同

• 抽样调查中的调查单位是按随机原则从全部总体单位中抽选出来的，不受人的主观因素所影响。
• 重点调查是选择一部分重点单位作为样本，且重点单位标志总量全部单位标志总量的绝大比重。
• 典型调查中的典型单位是在对总体情况分析的基础上有意识的抽选出来的。

（2）调查目的不同

• 抽样调查的目的，是以样本量来推断总体的数量特征；
• 重点调查的目的，是为了掌握现象总体的基本情况；
• 典型调查的目的，为了研究现象总体出现的新情况、新问题而进行的深入细致的调查。

（3）推断总体的可靠程度不同

• 抽样调查可以计算和控制推断的可靠程度。
• 重点调查不能推断总体总量；
• 典型调查中一定条件下可以推断总体总量，但又不知道可靠程度；

五、统计报表制度

统计报表是按国家统一规定的表式、统一的指标项目、统一的报送时间，自下而上定期提供统计资料的一种报告制度。

特点：

统一性

全面性

经常性

六、各种统计调查方式比较

项目类型	普查	抽样调查	重点调查	典型调查	统计报表
调查范围	全面	非全面	非全面	非全面	全面或非全面
调查时间	一次性	经常性或一次性	经常性或一次性	一次性	经常性
组织形式	专门调查	专门调查	报表制度或专门调查	专门调查	报表制度
调查单位的选择	—	按随机原则抽取样本单位	标志值在总体标志总量中占绝大比重的单位	具有典型代表的单位	—
调查结果能否推算总体	—	能	否	一般不能，但在划类选典和对准确性要求不高时也可以	—

第四节 统计调查方法

• 直接观察法
• 报告法
• 采访法
• 问卷法
• 网上调查法

---

第3章 统计整理

第一节 统计整理概述

统计整理的概念
根据统计研究的目的，对调查所得的原始资料进行科学的分类和汇总，为统计分析提供系统化、条理化资料的工作过程。
它是统计调查的继续和深化，又是统计分析的基础和前提。

统计整理的具体步骤

第二节 整理最基本手段—统计分组

统计整理最重要的环节之一是统计分组。

统计分组：根据现象的特点和统计研究的目的要求，按照某个（或几个）标志把总体划分为若干不同性质的组。

统计分组的作用：

1. 划分现象的类型
2. 揭示现象的内部结构
3. 分析现象间的依存关系

分组原则：

• 穷尽：使所有单位都有组可归。
• 互斥：一个单位之恶能分配到一个组内。

选择分组标志：

1. 符合统计研究的目的
2. 要从众多标志中，选择最能反映被研究现象本质特征的标志作分组标志。

第三节 数据汇总基本手段—分配数列

一、分配数列概念和种类

在统计分组的基础上，将总体所有的单位按某一标志进行归类排列。各组的单位数为频数，各组单位与总体单位总数之比叫频率。 将这些排列形成的表称为分配数列。

二、分配数列编制

上组限不计入

三、分配数列的图示

显示方法：

1. 直方图
2. 折线图
3. 曲线图
4. 条形图
5. 饼形图

曲线类型：

• 钟型分布
  特征是“两头小，中间大”，即靠近中间的变量值分布的次数多，靠近两边的变量值分布的次数少，其曲线图宛如一口钟。
  如：正态分布
  

• U型分布
  U型分布的形状与钟型分布相反，靠近中间的变量值分布次数少，靠近两端的变量值分布次数多，形成“两头大，中间小”的U型分布。
  如：人口死亡率分布（幼儿和老人死亡率高，而中青年死亡率低）
  

• J型分布
  如：供给曲线（正J型）、需求曲线（反J型）
  

第四节 数据展示基本方式—统计图表

一、统计表构成

二、统计表种类

---

第4章 总量指标与相对指标

第一节 总量指标

一、总量指标概念和作用

总量指标是反映一定时间、地点和条件下某种现象总体规模或水平的统计指标。它的表现形式是绝对数。

总量指标的作用：

1. 总量指标是对社会经济现象总体特征认识的起点指标。它可以反映一个国家的基本国情和国力，反映某部门或单位的人、财、物基本情况。
2. 总量指标是制定政策、编制计划、实行社会经济管理的基本依据之一。
3. 总量指标是计算相对指标、平均指标及其他分析指标的基础。因此总量指标的准确性直接影响到其他分析指标的质量。

二、总量指标的种类

（1）按说明总体的内容不同分为：

• 总体单位总量 —— 是用来反映统计总体内包含总体单位个数多少的总量指标。它用来表明统计总体的容量大小。
• 总体标志总量 —— 是统计总体各单位某一方面数量标志值的总和。

（2）按反映总体的时间状况不同分：

• 时期指标 —— 是反映社会经济现象在一段时间上发展变化结果的总量。

  1. 具有可加性
  2. 指标数值的大小与所属时期的长短直接相关
  3. 必须连续登记而得

• 时点指标 —— 反映社会经济现象在某一时刻或某一时点上的状况的总量。

  1. 不具有可加性
  2. 数值大小与登记时间的间隔长短无关
  3. 指标数值是间断计数的

三、总量指标的计量单位

1. 实物量单位是根据客观现象的物理属性而采用的计量单位。有自然单位、度量衡单位、复合单位和标准实物单位等。
2. 价值量单位也叫货币单位，是以货币为单位来度量现象总量的计量单位。用价值单位统计的总量指标也称为价值量指标。价值量指标具有广泛的综合性，但比较抽象，脱离了现象的物质内容。
3. 劳动量单位是用劳动时间表示的计量单位。常用的有工日和工时两种。劳动量单位是一种复合单位。一般用在定额生产行业。如机械行业，因生产周期长，产品结构复杂，不便运用前两种计量单位，故采用劳动量单位计量其劳动成果大小。

四、计算和运用总量指标应注意

• 要明确总量指标的涵义和计算范围；
• 计算口径要一致；
• 汇总时注意现象的同质性和计量单位的一致性。

第二节 相对指标

相对指标是说明现象之间数量对比关系的指标，用两个或两个以上有联系的指标数值对比来求得，其结果表现为相对数。
相对指标是说明现象之间数量对比关系的指标，用两个或两个以上有联系的指标数值对比来求得，其结果表现为相对数。

相对指标的作用：

1. 相对指标通过数量之间的对比，可以表明事物相关程度、发展程度。
2. 把现象的绝对差异抽象化，使原来无法直接对比的指标变为可比。
3. 说明总体内在的结构特征，为深入分析事物的性质提供依据。

相对指标的种类及其计算方法

（一） 结构相对指标
反映总体内部结构的一种综合指标。一般用百分数、成数或系数表示。

（二） 比例相对指标

（三） 比较相对指标

（四） 动态相对指标
将同—现象在不同时期的两个数值进行动态对比而得出的相对数，借以表明现象在时间上发展变动的程度。—般用百分数或倍数表示，也称为发展速度。
（五） 强度相对指标
在同一地区或单位内，两个性质不同而有一定联系的总量指标数值对比得出的相对数，是用来分析不同事物之间的数量对比关系，表明现象的强度、密度和普遍程度的综合指标。

（六） 计划完成情况相对指标
计划完成程度相对指标是社会经济现象在某时期内实际完成数值与计划任务数值对比的结果，一般用百分数来表示。

1. 计划数为绝对数和平均数时
   使用绝对数和平均数计算计划完成程度相对指标时，可直接用上述计算公式。

2. 计划数为相对数时
   

3. 计划执行进度相对数
   计划执行进度相对数=计划期期初至某时间止累计完成数/全期计划任务数×100%

4. 长期计划完成相对数（水平法时点）
   长期计划中只规定最后一年应达到的水平，若连续累计12个月实际完成数达到计划规定最末一年的水平，则剩余时间为提前完成计划的时间。
   长期计划完成相对数=长期计划末实际达到的水平/长期计划规定的末年水平

5. 长期计划完成相对数（累计法）
   长期计划完成相对数=长期计划期间实际累计完成数/长期计划规定任务数

第三节 计算和应用相对指标的原则

1. 正确选择对比的基数
2. 可比性原则
3. 相对指标和总量指标结合运用的原则
4. 各种相对指标综合应用的原则
5. 与经济内容结合

---

第5章 平均指标

第一节 平均指标的作用和分类

平均指标是总体各单位标志值在一定时间、地点条件下所达到的一般水平。
平均指标是衡量集中趋势的指标

平均指标作用：

1. 平均指标具有广泛的比较作用
2. 可以作为判断事物的依据或标准
3. 进行推算和预测，进行深入统计分析

平均指标的种类：

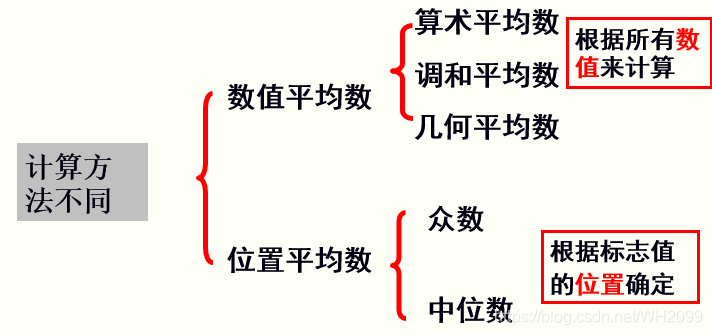
第二节 算数平均数

一、算术平均数含义

总体标志总量与总体单位总量的值。

分子分母为同一总体，分母是分子的承担者

二、简单算术平均数

条件：掌握了没有分组的总体各单位的标志值或已经有了标志总量和总体总量的资料。

三、加权算术平均数

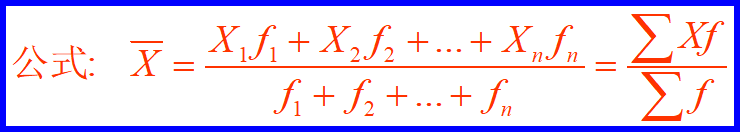
条件：分组资料
特点：平均数的大小既受其变量值大小的影响，又受其次数多少的影响

注意公式变形

• 绝对权数
  
• 相对权数
  

简单算术平均数与加权算术平均数的联系：
如果各组权数相同，权数就失去了权衡轻重的影响作用，加权算术平均数就变成了简单算术平均数。

四、算术平均数的数学性质

1. 各个变量值与其算术平均数的离差总和等于零。
2. 各个变量值与其算术平均数的离差平方总和为最小值。
3. 两个独立的同性质变量代数和的平均数等于其平均数的代数和。
4. 两个独立的同性质变量乘积的平均数等于其平均数的乘积。

第三节 调和平均数

一、概念

也称为倒数平均数。各变量值的倒数（1/Xi）的算术平均数的倒数。

二、计算

• 简单调和平均数
  
• 加权调和平均数
  

第四节 几何平均数

一、几何平均数的含义

n项标志值连乘积的n次方根。
适用于计算平均比率或平均速度。

二、几何平均数的计算

• 简单几何平均法
  
• 加权几何平均法
  

三、算术平均数、调和平均数与几何平均数的关系

算术平均数、调和平均数和几何平均数，统称为数值平均数，它们是所有变量值参加代数运算的结果，都要受到极端值大小的影响。算术平均数最容易受其影响，且受极大值的影响要大于受极小值的影响；调和平均数受极小值的影响要大于受极大值的影响；几何平均数受极端值的影响程度比前两者都小。因此，对同一资料计算这三种平均数，所得到的指标数值关系为：

第五节 位置平均数

一、中位数

将总体各单位按其标志值的大小顺序排列，处于数列中间位置的变量值。

特点：

1. 不受极端值的影响；
2. 在总体各标志值的差异较大时，具有较强的代表性。

中位数是一个位置代表值，利用中位数分析数据可以获得一些信息。有一半数比中位数大，有一半数比中位数小。即小于或大于这个中位数的数据各占一半。

中位数确定方法

• 未分组资料

  1. 先将总体各单位的标志值按大小顺序排列
  2. 确定中位数所在位置
     

• 单项式分组的资料

  1. 先对分组资料计算向上（或向下）累计频数（或频率）
  2. 确定中位数所在位置
  3. 在此位置上的变量值就是中位数
     

• 组距分组的资料

  1. 先对分组资料计算向上（或向下）累计频数（或频率）
  2. 确定中位数所在位置
  3. 由累计次数栏找到中位数所在组，再利用相应计算公式计算中位数
     

  下限公式
  

  上限公式
  

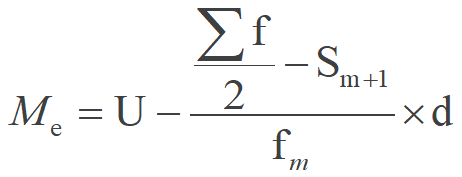
二、众数

总体中最普遍出现的变量值

特点：

1. 不受极端值的影响
2. 用来说明总体中大多数单位所达到的一般水平。

组距变量数列计算 （采用插补法）

• 下限公式
  

• 上限公式
  
  式中： L与 U 分别表示众数所在组的下限和上限；d 为众数所在组的组距；f_M0 、f_M0-1 和 f_M0+1 分别为众数所在组、前一组和后一组的次数。

三、四分位数—用3个点等分数据

四、各平均指标比较

指标	极端值影响	适用情况	其他特性
平均数	易受极端值影响	数据对称分布或接近对称分布时代表性较好	数学性质优良，实际中最常用
中位数	不受极端值影响	数据分布偏斜程度较大时代表性较好	—
众数	不受极端值影响	数据分布偏斜程度较大且有明显峰值时代表性较好	具有不惟一性

---

第6章 标志变异指标

---