OpenGL/GLUT实践：水面模拟——从单振源到 Gerstner Wave（电子科技大学信软图形与动画Ⅱ实验）

源码见GitHub：A-UESTCer-s-Code

1 实现效果

单振源实现效果如下：

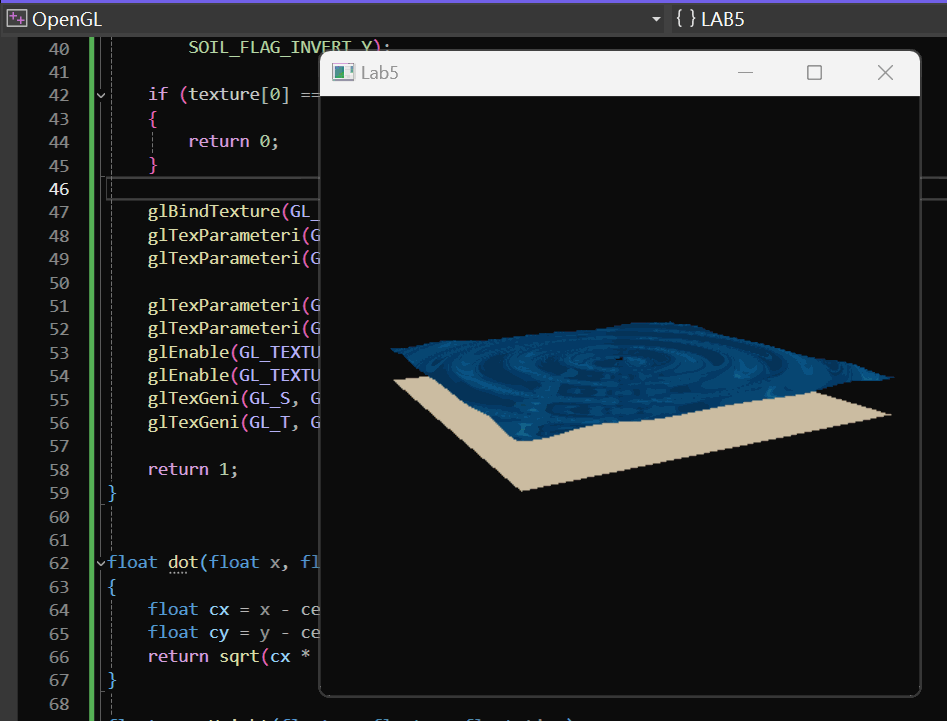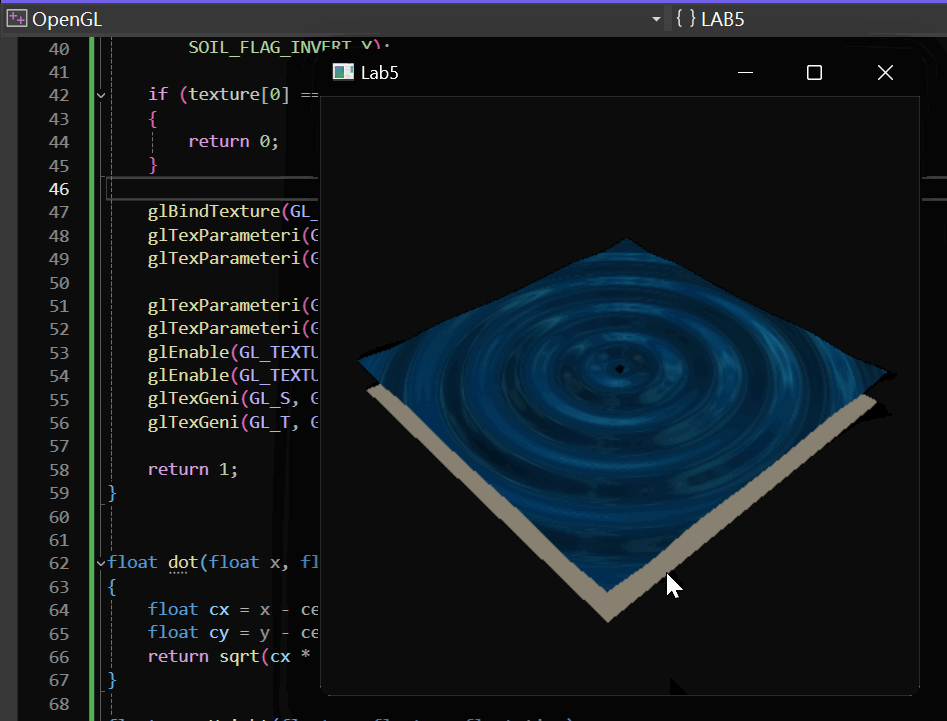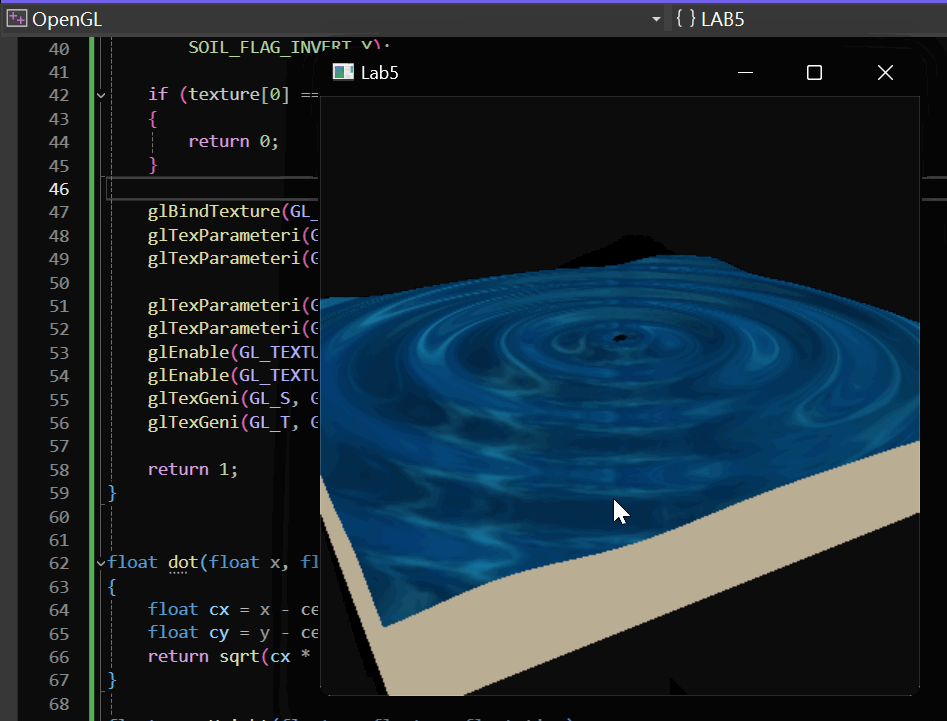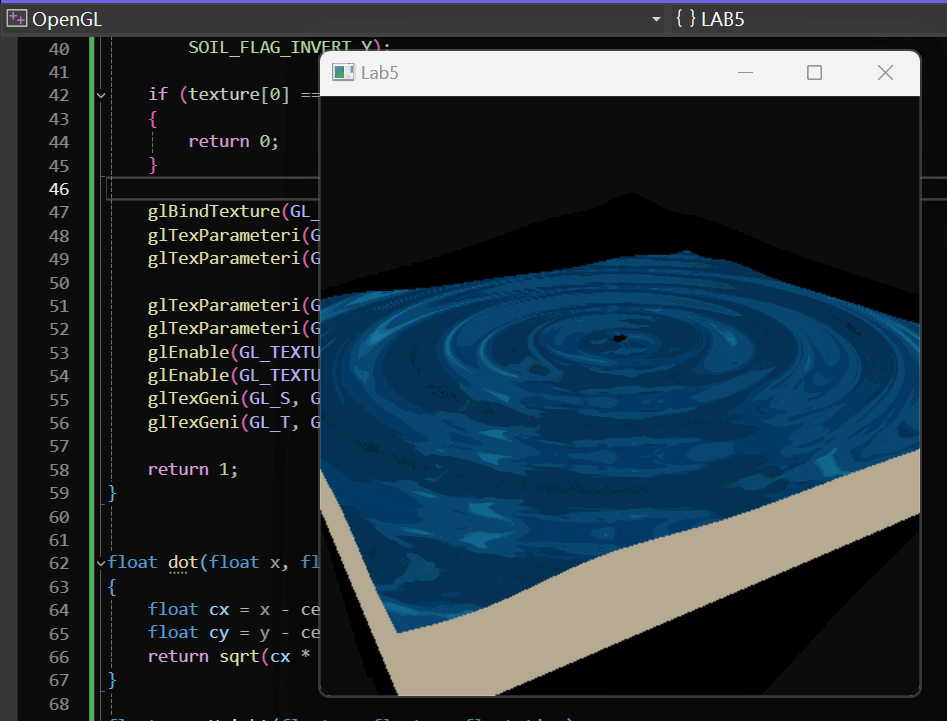
Gerstner Wave 实现效果如下：

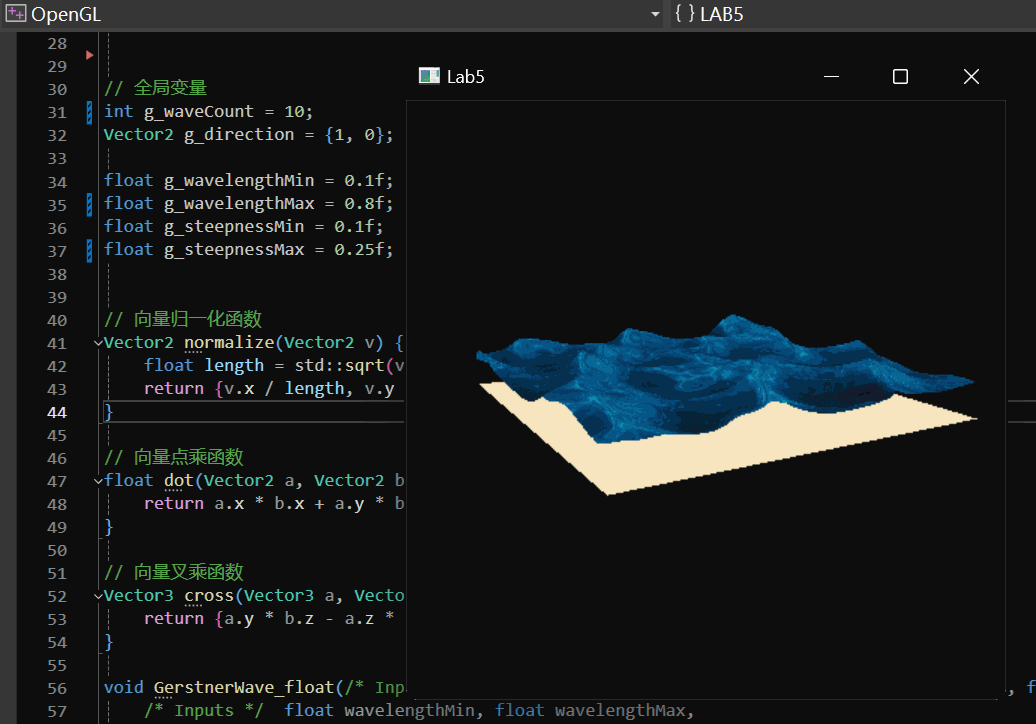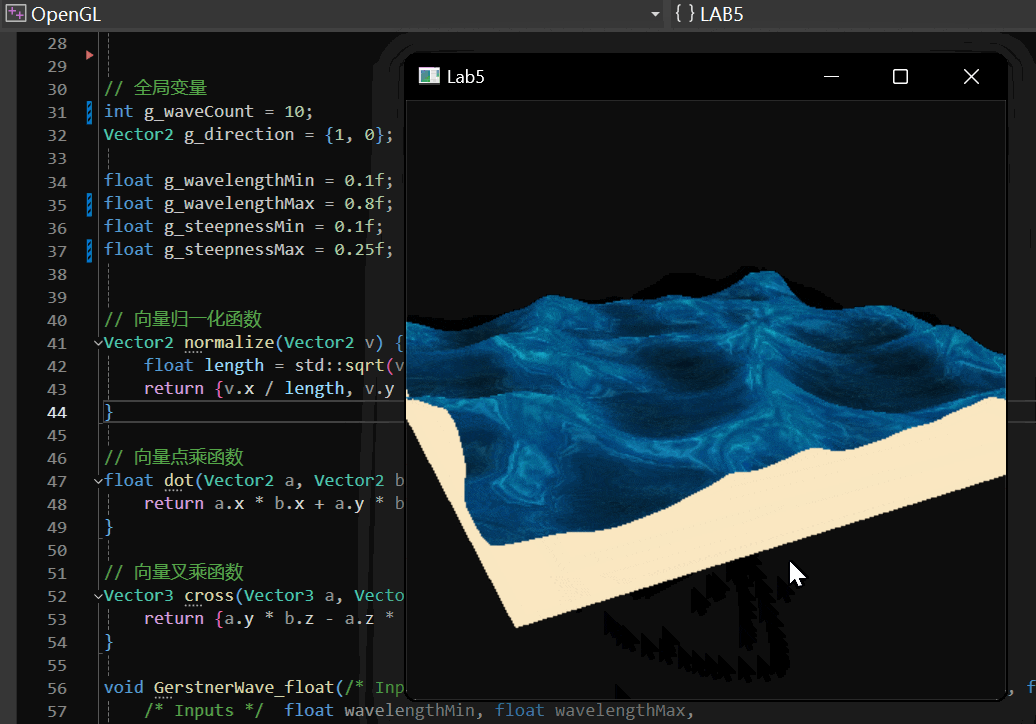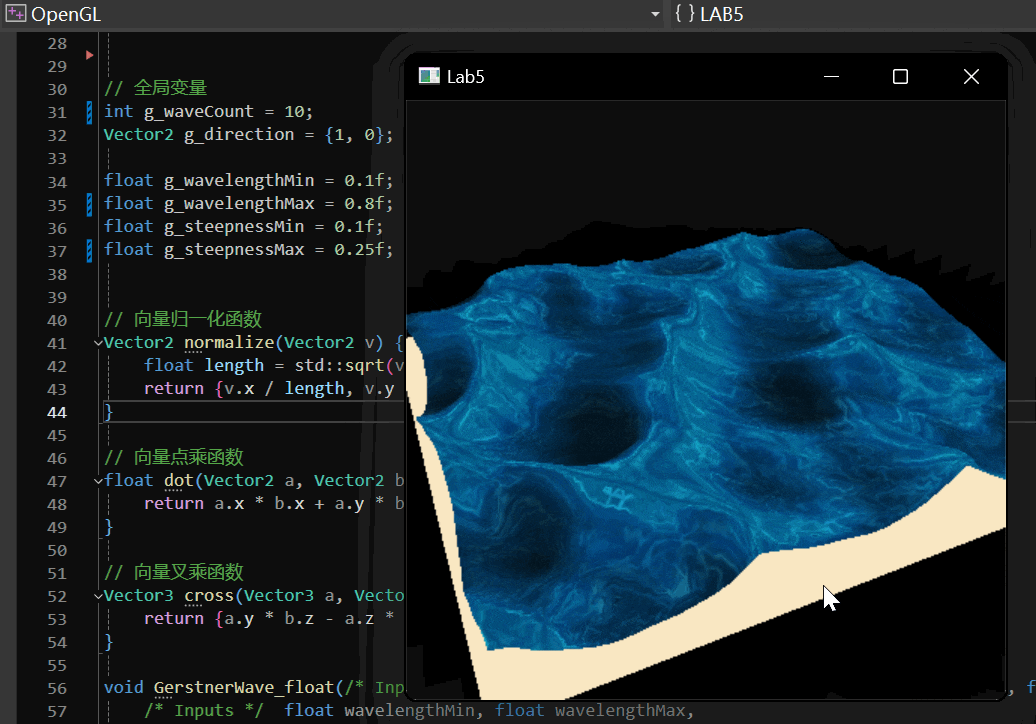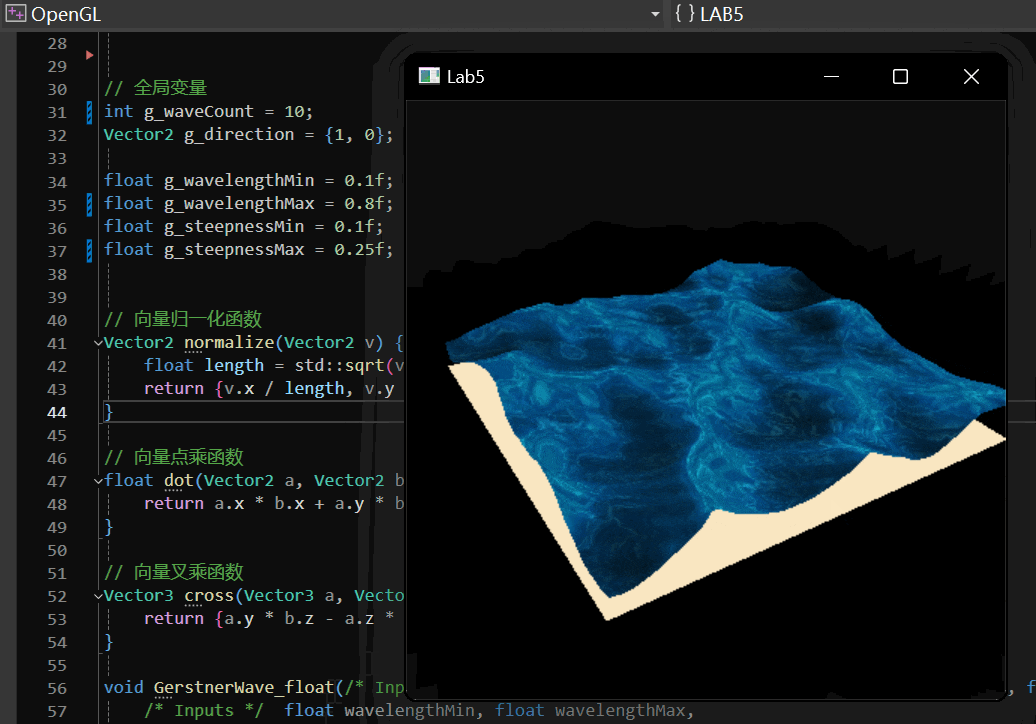
2 实现过程

2.1 简单水面模拟——单振源

2.1.1 水面高度函数

实现一个简单的水面模拟，其中只有一个振源位于原点：

1. 振源参数设置：

   振源的参数通过全局变量进行设置，包括振幅（amplitude）、波长（wavelength）、传播速度（speed）、以及振源的位置（center）。

   • 振源位于原点（0, 0），振幅为 0.01，波长为 0.3，传播速度为 -0.2。负号控制了波的传播方向。

2. 水面高度函数：

   水面的高度由一个函数 waveHeight 计算，该函数接受三个参数：位置（x, y）和时间（time），返回在该位置和时间下的水面高度。水面高度的计算涉及到振源的参数以及位置和时间的关系。

   • 首先计算频率（frequency），这里采用了频率和波长之间的关系公式：$frequency=\frac{2\pi }{wavelength}$。
   • 接着计算相位（phase），用来描述波的传播状态。相位的计算采用了速度和频率的乘积。
   • 最后，通过水面高度函数计算出位于位置（x, y）处、时间为 t 时的水面高度。其中，函数 dot 计算了网格点（x, y）到振源（0, 0）的距离，以用于后续计算。

   水面高度的计算采用了正弦函数，并根据振源参数和位置信息进行了调整。

3. 计算水面模拟中每个网格点处的法线向量，以便后续的渲染或物理模拟：

   • 函数 dWavedx 和 dWavedy：

     这两个函数分别计算了水面函数 H(x, y, t) 在网格点 (x, y) 处在 x 和 y 方向上的偏导数。在每个函数中：

     1. 首先计算了频率（frequency）、相位（phase）以及点到振源的距离（theta）。
     2. 然后利用这些参数计算了偏导数的近似值，其中使用了振幅、频率、位置和时间信息。这些偏导数描述了水面在不同方向上的变化情况。

   • 函数 waveNormal：

     这个函数根据 dWavedx 和 dWavedy 计算得到的偏导数来计算水面在每个点处的法线向量。

     1. 首先调用 dWavedx 和 dWavedy 函数计算得到 x 和 y 方向上的偏导数。
     2. 然后根据这些偏导数构造了法线向量。由于法线向量应该是单位向量，所以在构造过程中对其进行了归一化处理。
     3. 若归一化后的法线向量长度为 0，则默认法线向量为 (0, 1, 0)，表示垂直于水面的一个标准向上的向量。

2.1.2 水面建模

1. 构造网格：

   • 网格的大小由常量 RESOLUTION 指定，水面网格大小为 RESOLUTION * (RESOLUTION + 1)。
   • 水面高度数据存储空间大小为 3 * RESOLUTION * (RESOLUTION + 1)，其中 3 表示每个点的坐标和法线向量共占用三个分量。

2. 水面绘制：

   绘制水面的方法是链接相邻点的三个点 $(x,y,H(x,y,t))$ 绘制三角形，从而最终得到水面。采用 glDrawArray 或 glDrawElements 函数进行绘制，这两个函数能够通过少量的调用实现大量数据的绘制，提高绘制效率。

   glDrawArray 函数，其参数包括绘制类型、起始点索引和点的数目。使用 GL_TRIANGLE_STRIP 模式绘制，即相邻三角形共享一个边，这样存储时可以节省空间。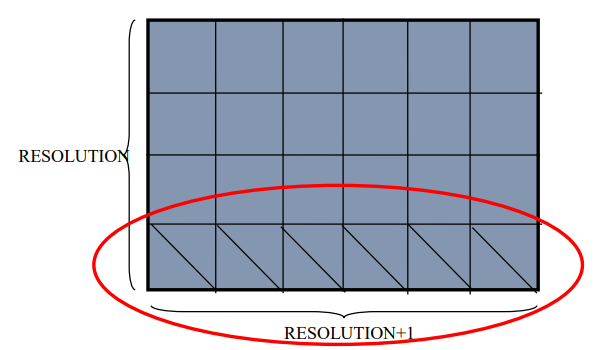

   
   • 为绘制红圈中的三角形，需要存储的顶点个数为 2 * (RESOLUTION + 1)，每个顶点坐标有三个分量，因此存储空间为 6 * (RESOLUTION + 1)。
   • 所以，整个水面的绘制需要的存储空间为 6 * RESOLUTION * (RESOLUTION + 1)。

使用两个一维数组 surface 和 normal 分别存储水面高度点的坐标和对应的法线向量。

static float surface[6 * RESOLUTION * (RESOLUTION + 1)];
static float normal[6 * RESOLUTION * (RESOLUTION + 1)];

2.1.3 openGL 渲染

(1) renderSense

renderSense() 用于渲染水面模拟的函数：

1. 清空缓冲区和设置视图：

   • glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT)：清空颜色缓冲区和深度缓冲区。
   • 设置视图的位置和旋转角度，根据 translate_z 和旋转角度 rotate_x 和 rotate_y 进行平移和旋转。

2. 构造水面网格：

   使用两个嵌套的循环来遍历水面网格中的每个点，计算其坐标和法线向量。计算每个点的坐标和法线向量，并存储在 surface 和 normal 数组中。

3. 绘制地面：

   使用 glBegin(GL_QUADS) 开始绘制四边形，表示地面。设置法线向量为 (0, 1, 0)，表示指向上方的法线。绘制四个顶点来定义四边形的形状。

4. 绘制水面：

   • 使用 glEnableClientState(GL_NORMAL_ARRAY) 和 glEnableClientState(GL_VERTEX_ARRAY) 启用法线和顶点数组。
   • 使用 glNormalPointer 和 glVertexPointer 分别指定法线和顶点数组的数据。
   • 使用 glDrawArrays(GL_TRIANGLE_STRIP, i * length, length) 绘制水面的三角形。

5. 绘制法线（可选）：

   如果 normals 不为 0，则绘制法线。绘制每个顶点的法线，并将其延长以便观察。

6. 交换缓冲区和重新绘制：

   使用 glutSwapBuffers() 来交换前后缓冲区，以显示绘制的图形。使用 glutPostRedisplay() 来请求重新绘制窗口，以持续更新图形。

其主要功能是根据当前时间动态地渲染水面模拟，并提供了选项来绘制法线和切换渲染模式。

(2) 其他

1. InitGL 函数是用来初始化 OpenGL 的环境。它设置了清除屏幕时的颜色，启用了深度测试，并设置了深度测试的函数。它还设置了透视修正的质量，并启用了光照。最后，它设置了颜色材质。
2. changeSize 函数是窗口大小改变时的回调函数。它首先检查新的高度是否为0，如果是，则将其设置为1，以防止除以0的错误。然后，它计算新的宽高比，并设置视口和透视投影。最后，它将当前矩阵模式设置为模型视图模式，并标记窗口需要重新绘制。
3. Keyboard 函数是键盘事件的回调函数。它根据按下的键来切换线框模式和法线显示，或者退出程序。

2.1.4 实现效果

初步的实现效果如下：

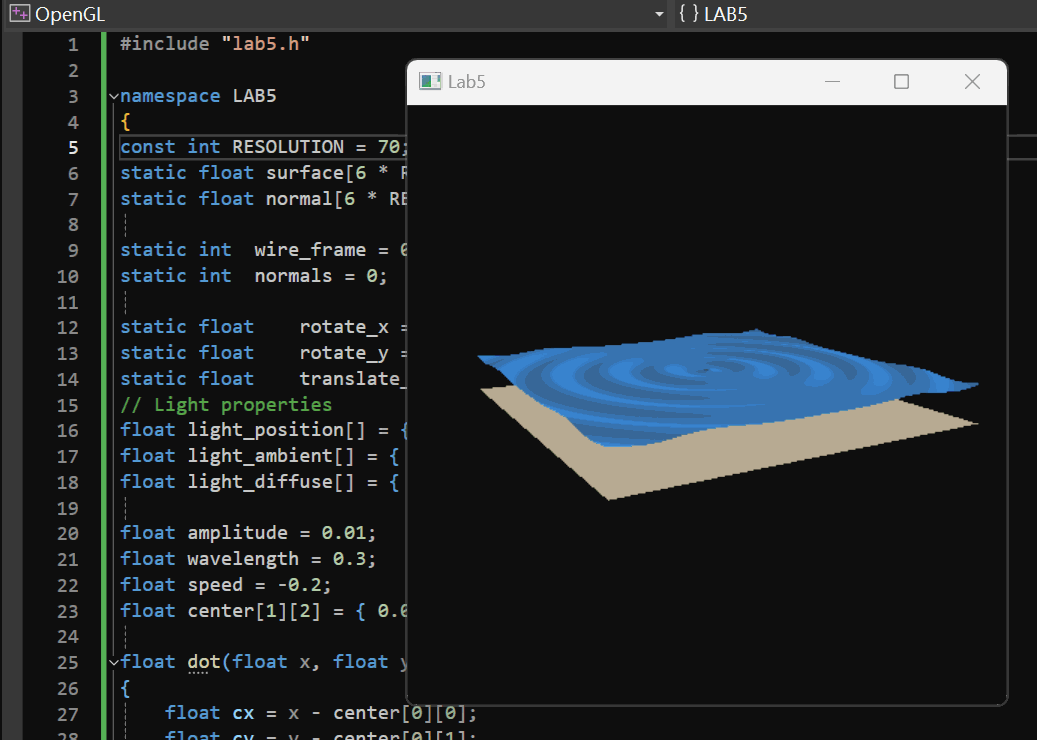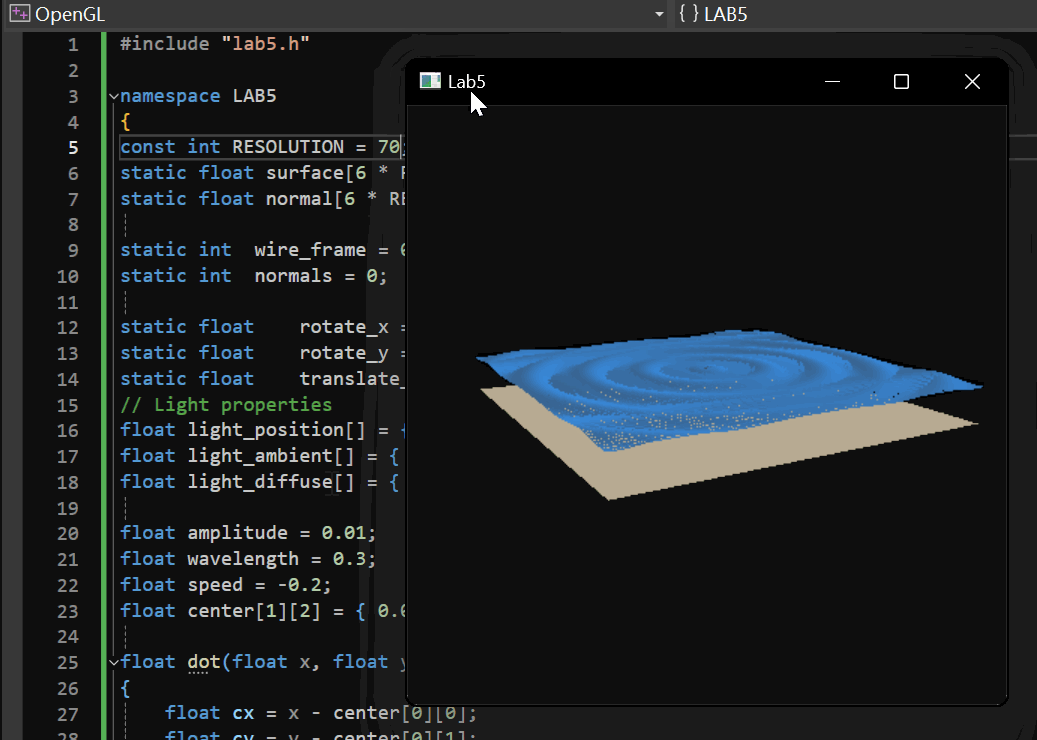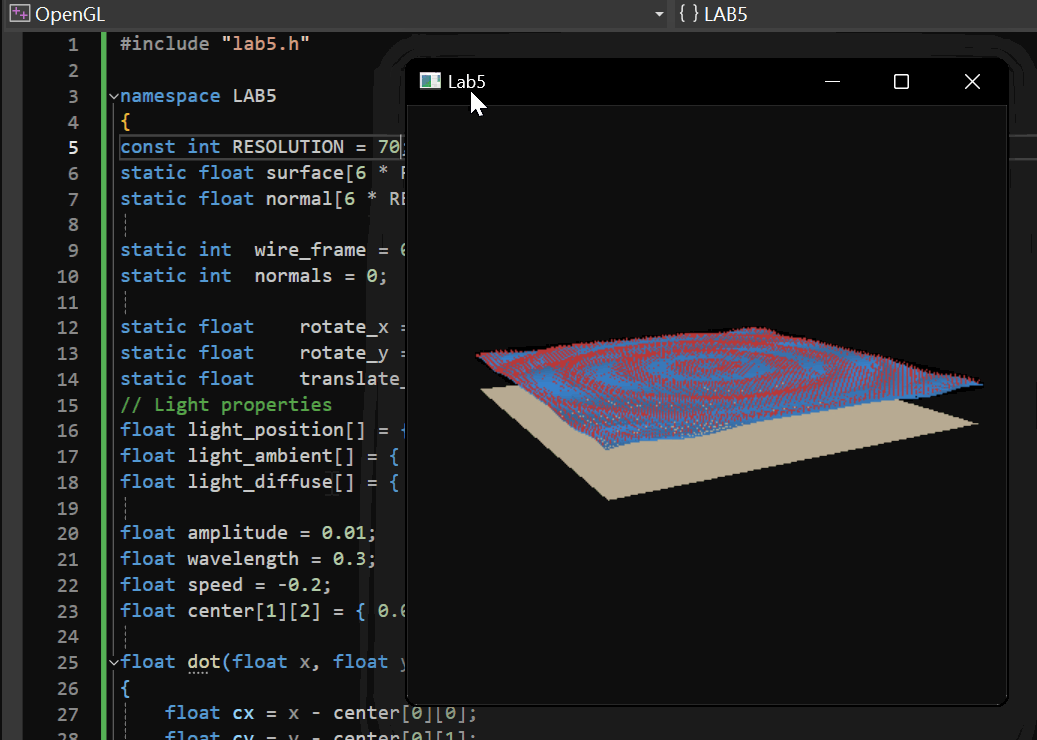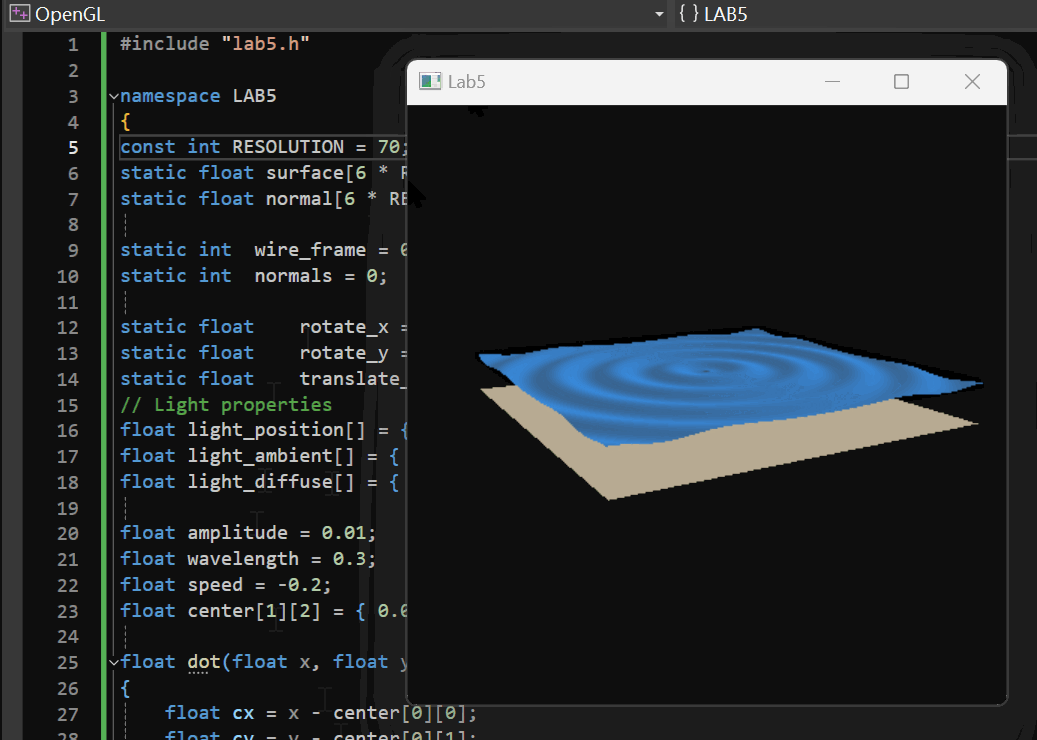
2.2 添加鼠标控制

实现通过鼠标控制观察物体的运动，主要包括监测鼠标点击事件和监测鼠标移动两个部分：

1. 监测鼠标点击事件：

   • 注册回调函数 glutMouseFunc 来响应鼠标点击事件，在主函数中调用。该函数接受一个回调函数作为参数，用于处理鼠标点击事件。
   • 回调函数 Mouse 接受四个参数，分别表示按下或释放了哪个键、按键的状态、以及鼠标相对于窗口客户区域左上角的坐标。
   • 在 Mouse 函数中，根据按下的鼠标键不同，记录左键和右键的状态，并更新鼠标位置。

2. 监测鼠标移动：

   • 注册活跃移动函数 glutMotionFunc 来响应鼠标移动事件，在主函数中调用。该函数接受一个回调函数作为参数，用于处理鼠标移动事件。
   • 回调函数 mouseMotion 接受两个参数，表示鼠标相对于窗口客户区域左上角的坐标。
   • 在 mouseMotion 函数中，根据鼠标按下的状态不同，实现不同的操作：
     • 如果左键被按下，则根据鼠标在 y 轴和 x 轴上的移动来旋转物体，并限制旋转角度在 -90° 到 90° 之间。
     • 如果右键被按下，则根据鼠标在 x 轴上的移动来控制物体沿 z 轴的平移，实现放大缩小的效果，并限制平移范围在 0.5 到 10 之间。
   • 在处理完鼠标移动后，更新 xold 和 yold 记录鼠标位置，并通过 glutPostRedisplay 请求重新绘制窗口以更新画面。

通过这两个函数，可以实现通过鼠标控制观察物体的旋转和缩放操作，从而方便用户观察水面模拟的效果。

实现效果：

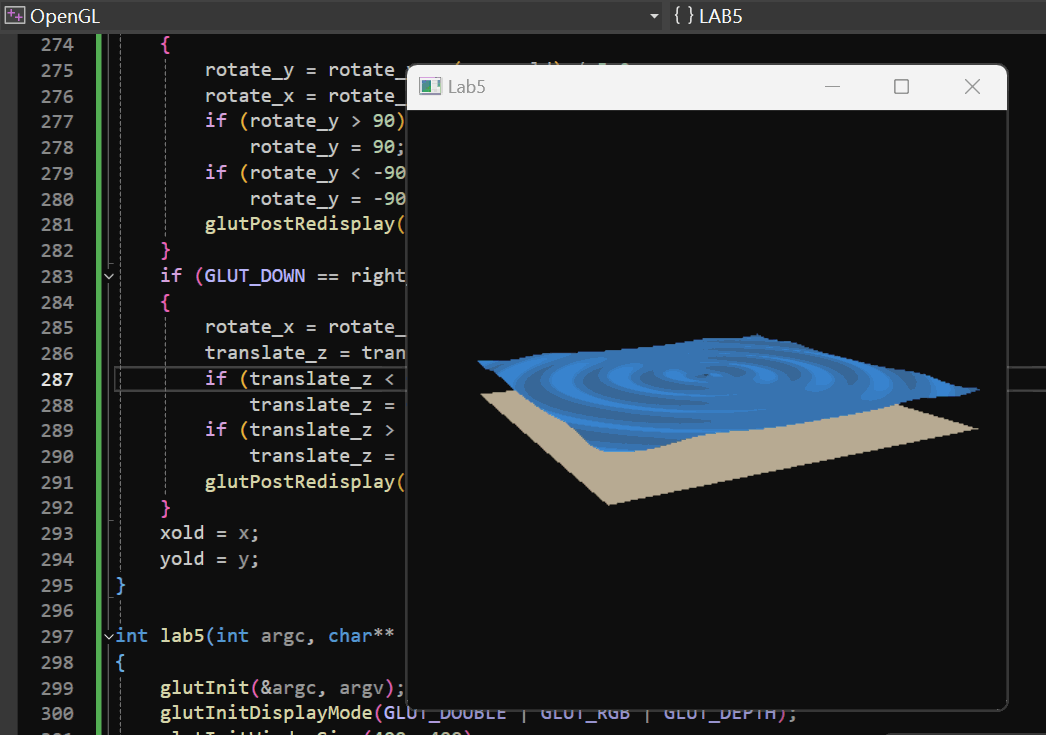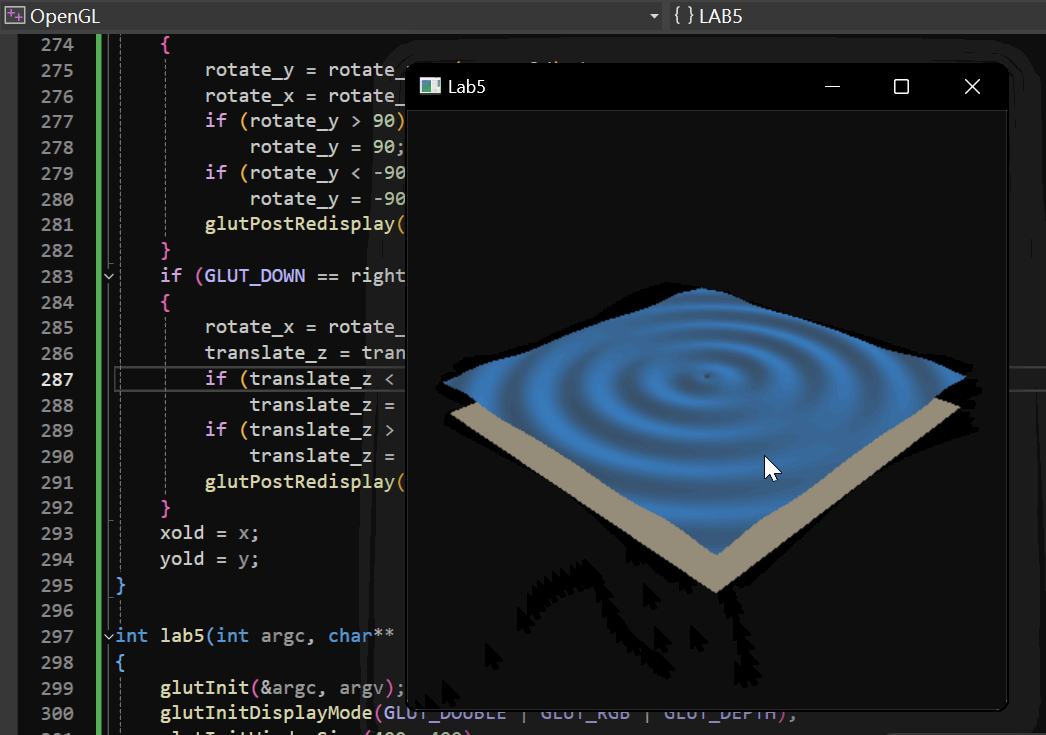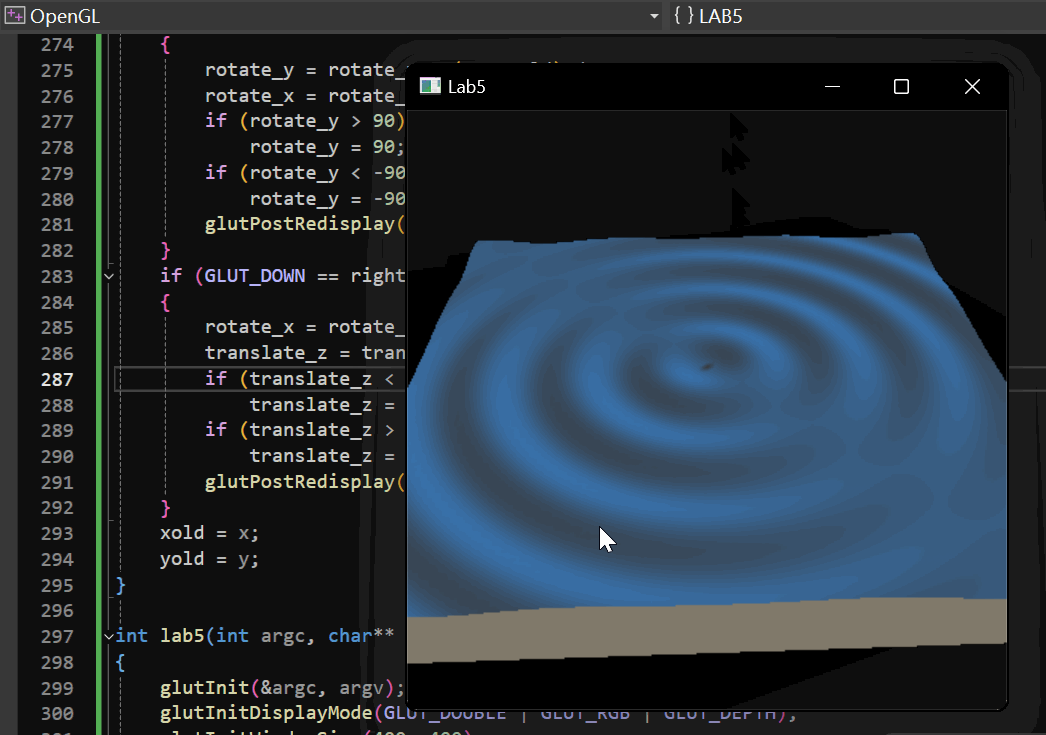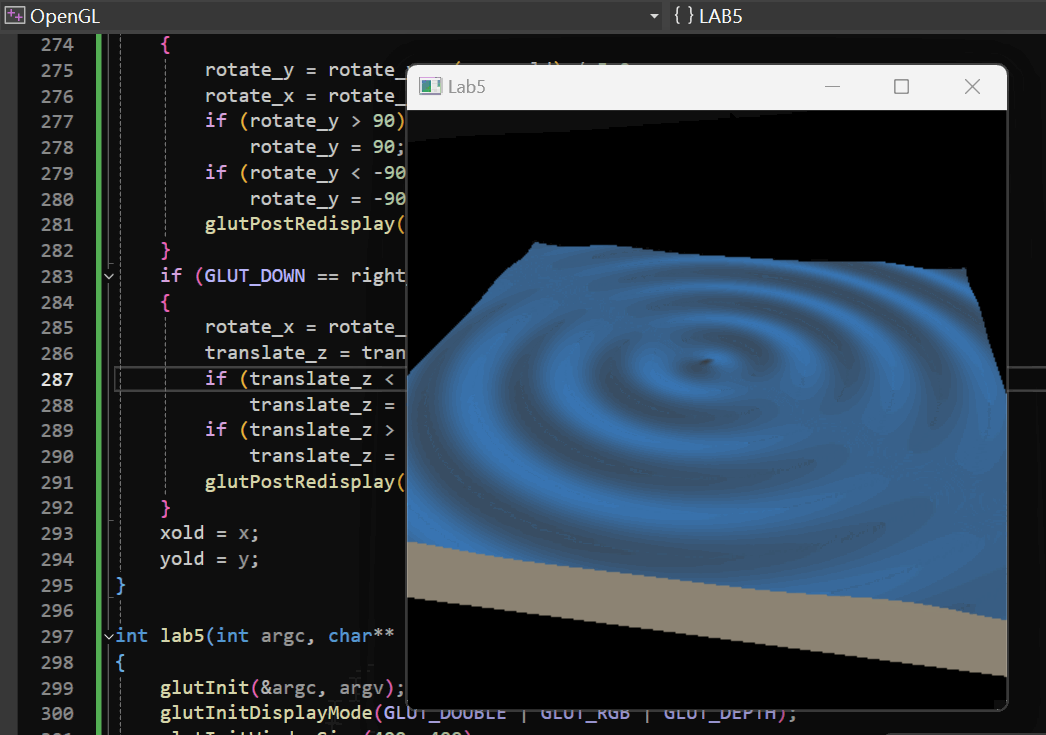
2.3 添加纹理

为了让水面更生动，我们为水面添加如下纹理，载入纹理和修改初始化函数的步骤：

1. 载入纹理：

   • 使用 SOIL_load_OGL_texture 函数载入纹理图片，并将其存储在 texture[0] 中。
   • 设置纹理参数，包括放大和缩小过滤器，以及纹理坐标的环绕方式。
   • 启用纹理坐标的自动生成，使用 glEnable(GL_TEXTURE_GEN_S) 和 glEnable(GL_TEXTURE_GEN_T) 启用纹理坐标的自动生成。
   • 使用 glTexGeni 函数设置纹理坐标的自动生成模式为球形映射。

2. 修改初始化函数：

   • 在初始化函数 InitGL 中调用 LoadGLTextures 函数，载入纹理。

   在 renderScene 函数中，在绘制地面之前禁用纹理，然后在绘制水面之前再次启用纹理。可以使用 glDisable(GL_TEXTURE_2D) 来禁用纹理，然后使用 glEnable(GL_TEXTURE_2D) 来启用纹理。

通过以上步骤，可以为水面模拟添加纹理，使其更加生动。

实现效果如下：

2.4 多个振源组合

实现一个多振源组合的水面模拟，创建更复杂的水面效果。

全局变量： numWaves 指定了振源的个数。振源参数包括振幅 amplitude，波长 wavelength，传播速度 speed，以及振源中心 center。

1. 水面高度函数：

   • dot 函数计算第 i 个振源到点 (x, y) 的距离。
   • wave 函数计算第 i 个振源在位置 (x, y) 处的水面高度。
   • waveHeight 函数遍历所有振源，累加每个振源的高度值，得到最终的水面高度。

2. 法线计算：

   • dWavedx 和 dWavedy 函数分别计算第 i 个振源在 x 和 y 方向上的偏导数。
   • waveNormal 函数遍历所有振源，累加每个振源的偏导数，计算得到最终的法线向量。

通过以上修改和扩展，可以实现多个振源的水面模拟，生成更加复杂的波动效果。每个振源的影响叠加在一起，形成一个动态的水面，这些振源可以根据需要进行配置，以模拟不同的水面环境。

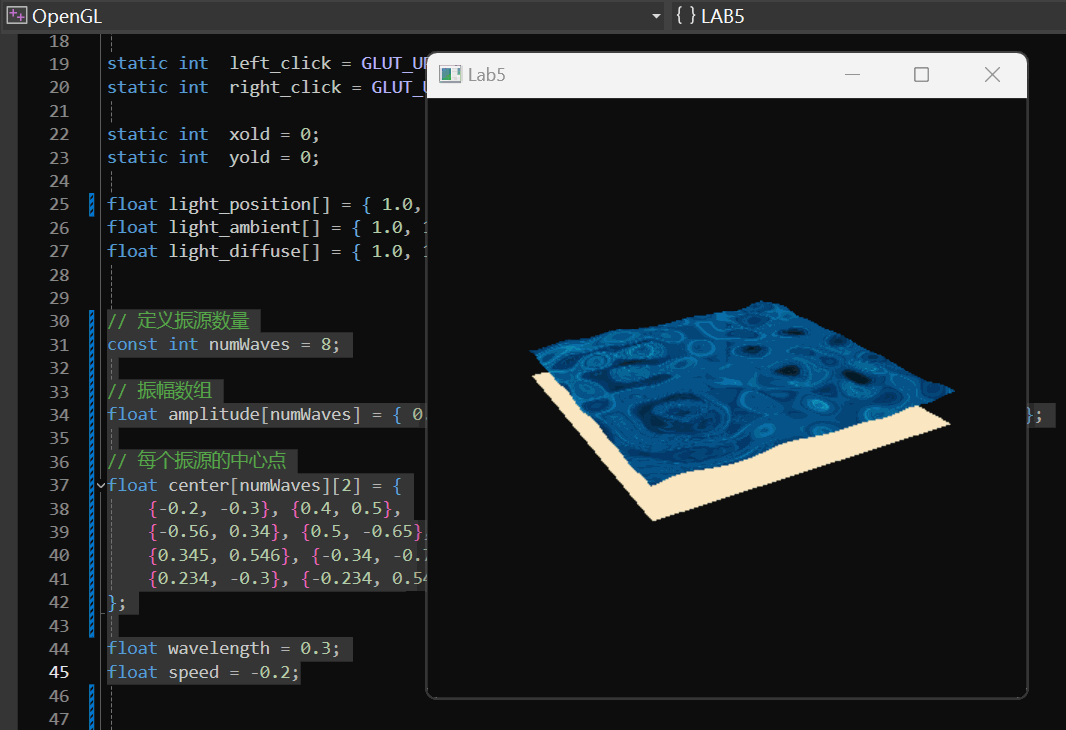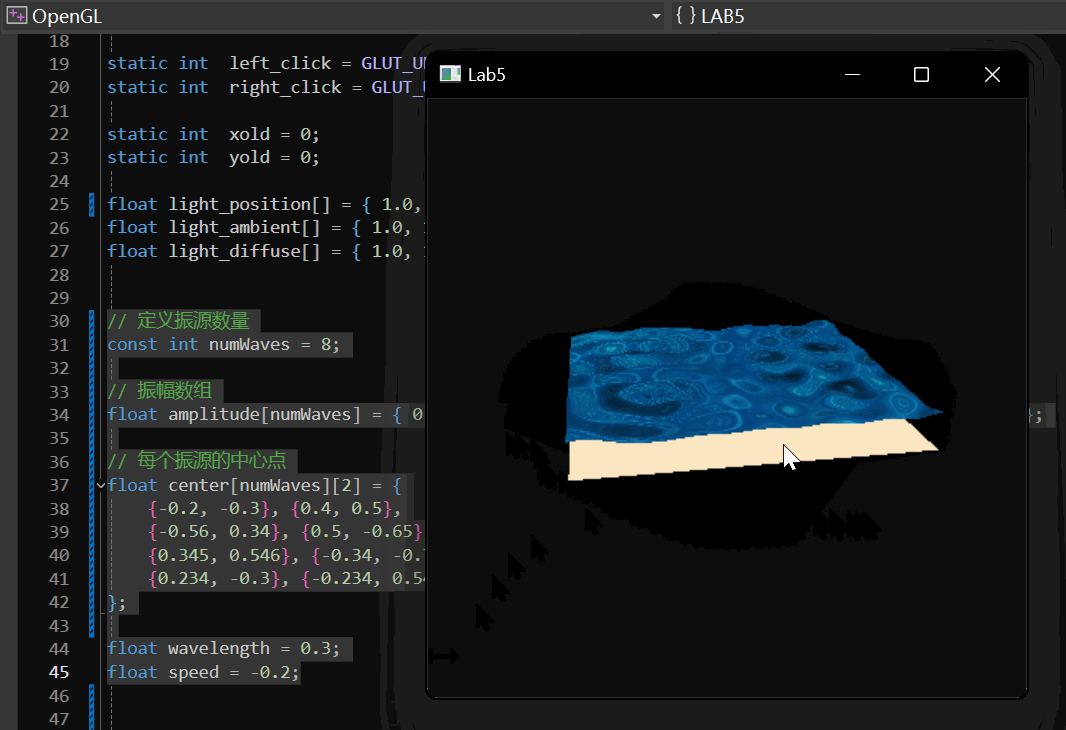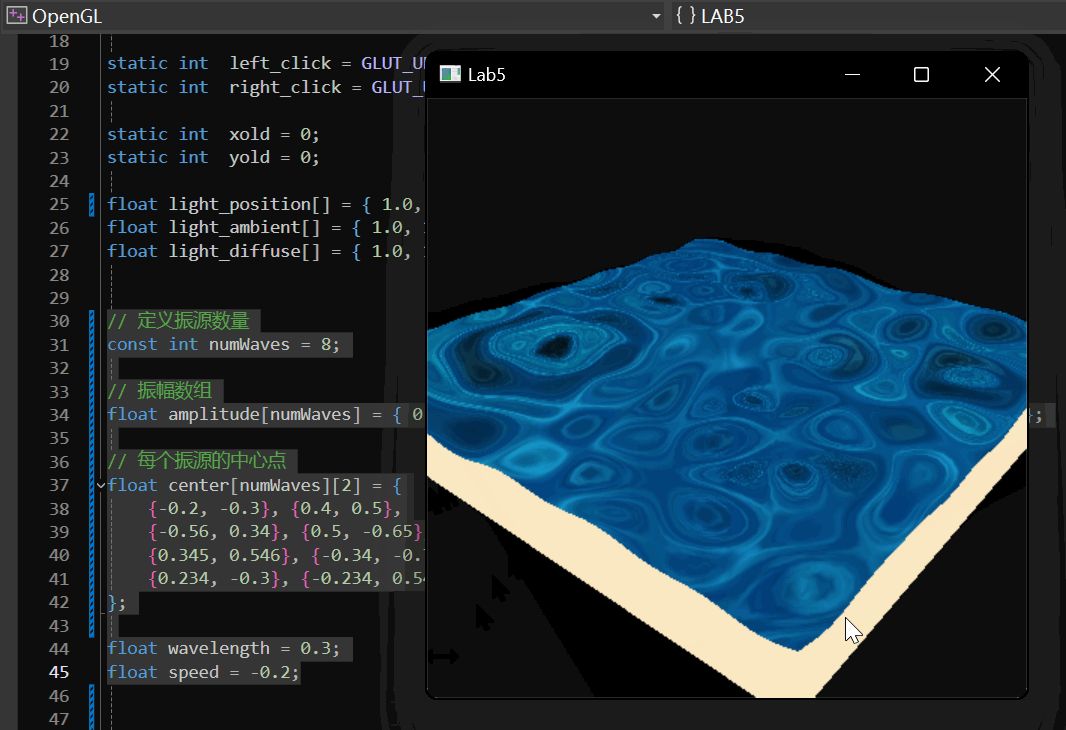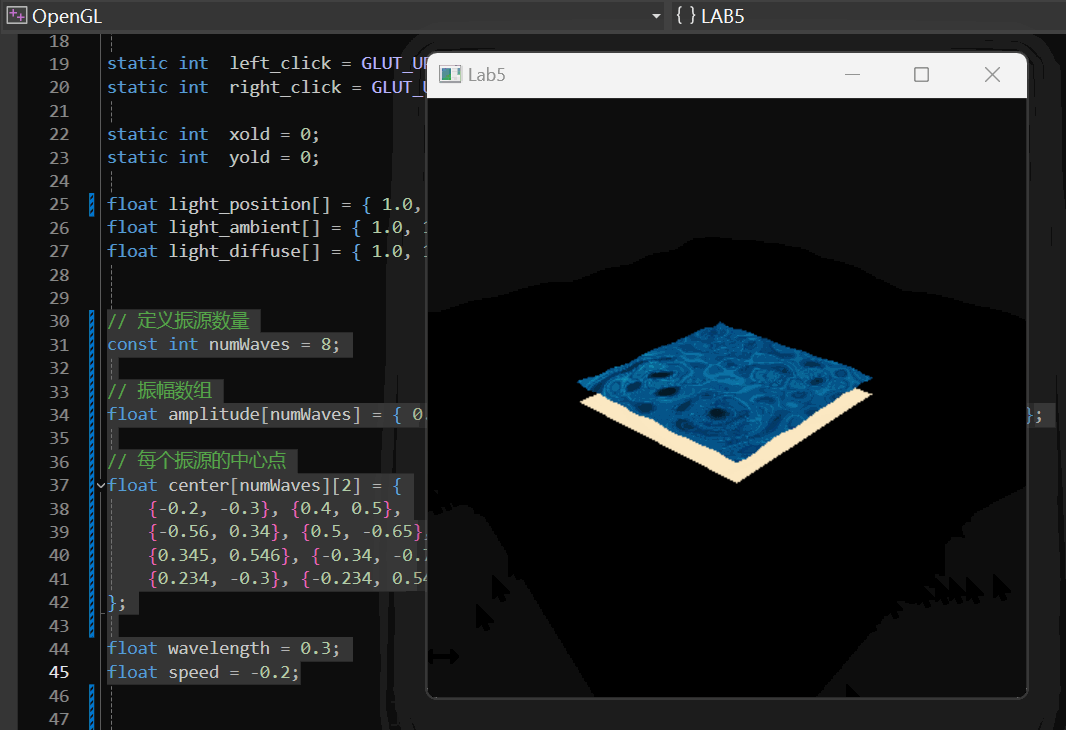
我们随机设置了8个振源：

// 定义振源数量
const int numWaves = 8;

// 振幅数组
float amplitude[numWaves] = { 0.006, 0.00654, 0.006, 0.004, 0.005, 0.00456, 0.0065, 0.005 };

// 每个振源的中心点
float center[numWaves][2] = {
	{-0.2, -0.3}, {0.4, 0.5},
	{-0.56, 0.34}, {0.5, -0.65},
	{0.345, 0.546}, {-0.34, -0.76},
	{0.234, -0.3}, {-0.234, 0.546}
};

实现效果：

2.5 Gerstner Wave 模型

2.5.1 原理

Gerstner Wave模型是一种用于模拟水面波动的数学模型，其基本思想是通过叠加多个圆周运动的波形来模拟真实的水面波动。下面是Gerstner Wave模型的一些关键点：

1. 圆周运动： Gerstner Wave模型中，每个波动被建模为沿着水平方向和垂直方向的圆周运动。每个波动的振幅和相位随着时间的变化而变化，从而产生起伏的水面效果。
2. 振幅和波长： 波的振幅控制波的高度或强度，而波长则控制波的密度或波长。通过调整这两个参数，可以实现不同形态的水面波动。
3. 陡度： Gerstner Wave模型可以生成比正弦波更加尖锐陡峭的波峰。通过调整陡度参数，可以控制波峰的陡峭程度，使波浪更加逼真。
4. 波的方向： 每个波动可以沿着不同的方向传播，从而模拟出复杂的水面波动。通过指定波的传播方向，可以实现更加自然的水面效果。

多波叠加： Gerstner Wave模型可以通过叠加多个波动来模拟真实的水面效果。通过调整每个波动的参数，可以实现更加丰富和复杂的水面波动。

多个Gerstner Wave的叠加是模拟复杂水波效果的关键。在这里，我们需要将多个单独的Gerstner Wave的效果叠加起来，以形成更加真实和生动的水面效果。计算公式如下所示：

$$X(x,z,t)=x+\sum _{i=1}^N{D}_x^i{A}_i\cdot \cos (k\cdot {\mathbf{D}}_i\cdot (x,z)-w_{i}t)$$

$$Y(x,z,t)=\sum _{i=1}^N{A}_i\cdot \sin (k\cdot {\mathbf{D}}_i\cdot (x,z)-w_{i}t)$$

$$Z(x,z,t)=z+\sum _{i=1}^N{D}_x^i{A}_i\cdot \cos (k\cdot {\mathbf{D}}_i\cdot (x,z)-w_{i}t)$$

其中：

• $N$ 是Gerstner Wave的数量；
• $A_i$ 是第 $i$ 个波的振幅；
• $D_i$ 是第 $i$ 个波的方向向量；
• $k$ 是波数，$k=\frac{2\pi }{\lambda }$，其中 $\lambda$ 是波长；
• $w_i$ 是角频率，$w_i=\sqrt{g\cdot k}$，其中 $g$ 是重力加速度。

这些公式表示了在给定时间 $t$ 和空间坐标 $(x,z)$ 处水面的变形情况。我们可以通过对每个波的贡献进行叠加来计算最终的水面形态。

在代码中，我们将使用向量表示每个波的属性。每个波的信息用一个Vector4表示，其中x分量表示波长，y分量表示振幅，zw分量表示波的方向。

2.5.2 具体实现

1） 全局变量与工具函数

在实现Gerstner Wave模型时，我们需要定义一些全局变量和实用函数来帮助我们进行向量计算和波的叠加。下面是具体的定义和代码解释：

// 全局变量
int g_waveCount = 10;  // Gerstner Wave的数量
Vector2 g_direction = {1, 0};  // 波的初始方向

float g_wavelengthMin = 0.1f;  // 最小波长
float g_wavelengthMax = 0.8f;  // 最大波长
float g_steepnessMin = 0.1f;   // 最小陡度
float g_steepnessMax = 0.25f;  // 最大陡度

这些全局变量用于控制Gerstner Wave模型的基本属性：

• g_waveCount 指定了波的数量。
• g_direction 设置了波的初始传播方向。
• g_wavelengthMin 和 g_wavelengthMax 设置了波长的范围。
• g_steepnessMin 和 g_steepnessMax 设置了波陡度的范围。

向量归一化函数：

// 向量归一化函数
Vector2 normalize(Vector2 v) {
    float length = std::sqrt(v.x * v.x + v.y * v.y);
    return {v.x / length, v.y / length};
}

normalize 函数用于将一个二维向量归一化，使其长度为1。归一化后的向量方向不变，但其长度为1。这对于计算方向向量非常重要。

向量点乘函数：

// 向量点乘函数
float dot(Vector2 a, Vector2 b) {
    return a.x * b.x + a.y * b.y;
}

dot 函数计算两个二维向量的点积。点积是一个标量，反映了两个向量的相对方向。它在计算波的相位时会用到。

向量叉乘函数：

// 向量叉乘函数
Vector3 cross(Vector3 a, Vector3 b) {
    return {a.y * b.z - a.z * b.y, a.z * b.x - a.x * b.z, a.x * b.y - a.y * b.x};
}

cross 函数计算两个三维向量的叉积。叉积是一个向量，垂直于输入的两个向量。在三维空间中计算法线或处理向量之间的几何关系时会用到。

2） Gerstner Wave主函数

函数 GerstnerWave_float 用于计算给定位置的水面变形及法线。函数输入包括初始位置、波的数量、波的方向、速度、波长和陡度的最小最大值，输出变形后的位置和法线向量。

函数原型：

void GerstnerWave_float(
    /* Inputs */  Vector3 positionIn, int waveCount, Vector2 direction, float speed,
    /* Inputs */  float wavelengthMin, float wavelengthMax,
    /* Inputs */  float steepnessMin, float steepnessMax,
    /* Outputs */ Vector3& positionOut, Vector3& normalOut)

函数内部变量：

float x = 0, y = 0, z = 0;
float bx = 0, by = 0, bz = 0;
float tx = 0, ty = 0, tz = 0;
positionOut = positionIn;

unsigned int randX = 12345, randY = 67890;

这些变量用于累积波的影响，以及保存变形后的位置和法线。

主循环：

1. 随机方向生成与归一化：

   randX = (randX * 1103515245) + 12345;
   randY = (randY * 1103515245) + 12345;
   Vector2 d = Vector2(sin((float)randX / 801571.f), cos((float)randY / 10223.f));
   d = normalize(d);
   

   每个波的方向是随机的，通过随机数生成器生成，并且归一化。

2. 计算波的参数：

   step = pow(step, 0.75f);
   float wavelength = wavelengthMin + step * (wavelengthMax - wavelengthMin);
   float steepness = steepnessMin + step * (steepnessMax - steepnessMin);
   
   float k = 2 * M_PI / wavelength;
   float w = sqrt(9.8 * k);
   float a = steepness / k;
   

   计算波长、陡度、波数 $k$ 和角频率 $w$，以及振幅 $a$。

   • step：这是一个在0到1之间的值，表示当前波在所有波中的相对位置。pow(step, 0.75f)是一个调整函数，用于调整波长和陡峭度的分布。这个函数会使得较小的波长和陡峭度更常见，较大的波长和陡峭度较少见。
   • wavelength：波长，是波的长度。它是根据step在wavelengthMin和wavelengthMax之间插值得到的。
   • steepness：陡峭度，表示波的高度。它也是根据step在steepnessMin和steepnessMax之间插值得到的。
   • k：波数，是波长的倒数，用于表示波的密度。它的值是2 * M_PI / wavelength。
   • w：角频率，表示波的速度。它的值是sqrt(9.8 * k)，其中9.8是重力加速度。
   • a：振幅，表示波的大小。它的值是steepness / k，表示陡峭度和波数的比值。

3. 计算每个波的相位值和叠加效果：

   Vector2 wavevector;
   wavevector.x = k * d.x;
   wavevector.y = k * d.y;
   
   float value = dot(Vector2(positionIn.x, positionIn.z), wavevector) - w * speed * 0.1f;
   
   x += d.x * a * cos(value);
   z += d.y * a * cos(value);
   y += a * sin(value);
   
   bx += d.x * d.x * k * a * -sin(value);
   by += d.x * k * a * cos(value);
   bz += d.x * d.y * k * a * -sin(value);
   
   tx += d.x * d.y * k * a * -sin(value);
   ty += d.y * k * a * cos(value);
   tz += d.y * d.y * k * a * -sin(value);
   

   根据相位值value，分别计算每个波对位置(x, y, z)和切线、法线的贡献。

   • wavevector：波向量，由波数k和波的方向向量d的乘积得到。
   • value：波的相位，由输入位置和波向量的点积，减去角频率w、速度speed和时间的乘积得到。
   • x、y和z：Gerstner波的位置，根据Gerstner波的公式计算。x和z是水平位置，y是垂直位置。
   • bx、by和bz：用于计算法向量的辅助变量，根据Gerstner波的公式计算。
   • tx、ty和tz：也是用于计算法向量的辅助变量，根据Gerstner波的公式计算。

   给定一个输入位置，它会计算出该位置在Gerstner波影响下的新位置和法向量。这可以用来模拟水面的波动效果。

4. 计算最终的输出位置和法线：

   positionOut.x = positionIn.x + x;
   positionOut.z = positionIn.z + z;
   positionOut.y = y;
   
   Vector3 bitangent = Vector3(1 - std::min(1.f, bx), by, bz);
   Vector3 tangent = Vector3(tx, ty, 1 - std::min(1.f, tz));
   normalOut = cross(tangent, bitangent);
   

5. 位置更新：叠加所有波的影响后，更新最终的变形位置 positionOut。

6. 法线计算：计算 bitangent 和 tangent，通过它们的叉积 cross 得到水面的法线 normalOut。

3） RenderScene修改

计算位置和法线

RenderScene中首先我们计算每个网格顶点的变形位置和法线，并将这些结果存储在 surface 和 normal 数组中。通过遍历网格的每个顶点，并调用 GerstnerWave_float 函数计算波浪效应。

总体计算步骤：

1. 遍历网格顶点：双重循环遍历网格的每个顶点。
2. 调用 GerstnerWave_float：计算顶点变形位置和法线，并将结果存储在 surface 和 normal 数组中。
3. 处理前一行顶点的值：如果顶点不在第一行，复制前一行的值；否则，计算初始位置处的变形位置。
4. 计算法线：将计算出的法线存储在 normal 数组中。

遍历网格顶点：

for (j = 0; j < RESOLUTION; j++) {
    y = (j + 1) * delta - 1;
    for (i = 0; i <= RESOLUTION; i++) {
        indice = 6 * (i + j * (RESOLUTION + 1));
        x = i * delta - 1;

遍历网格的每个顶点。RESOLUTION 定义了网格的分辨率，delta 是每个网格单元的尺寸。y 和 x 分别表示当前顶点的坐标。

调用 GerstnerWave_float 计算顶点变形：

Vector3 positionIn = Vector3(x, 0, y);
Vector3 positionOut, normalOut;
GerstnerWave_float(positionIn, g_waveCount, g_direction, t, g_wavelengthMin, g_wavelengthMax, g_steepnessMin, g_steepnessMax, positionOut, normalOut);
surface[indice + 3] = positionOut.x;
surface[indice + 4] = positionOut.y;
surface[indice + 5] = positionOut.z;

调用 GerstnerWave_float 函数计算当前顶点的变形位置和法线。positionIn 是输入的顶点位置，positionOut 和 normalOut 分别是输出的变形位置和法线。计算结果存储在 surface 数组中。

处理前一行顶点的值：

if (j != 0) {
    preindice = 6 * (i + (j - 1) * (RESOLUTION + 1));
    surface[indice] = surface[preindice + 3];
    surface[indice + 1] = surface[preindice + 4];
    surface[indice + 2] = surface[preindice + 5];
} else {
    positionIn = Vector3(x, 0, -1);
    GerstnerWave_float(positionIn, g_waveCount, g_direction, t, g_wavelengthMin, g_wavelengthMax, g_steepnessMin, g_steepnessMax, positionOut, normalOut);
    surface[indice] = positionOut.x;
    surface[indice + 1] = positionOut.y;
    surface[indice + 2] = positionOut.z;
}

如果当前顶点不在第一行，我们将前一行的值复制到当前顶点。否则，我们计算初始位置在 (x, 0, -1) 处的变形位置并存储。

计算法线：

normal[indice] = normalOut.x;
normal[indice + 1] = normalOut.y;
normal[indice + 2] = normalOut.z;

positionIn = Vector3(surface[indice + 3], 0, surface[indice + 5]);
GerstnerWave_float(positionIn, g_waveCount, g_direction, t, g_wavelengthMin, g_wavelengthMax, g_steepnessMin, g_steepnessMax, positionOut, normalOut);
normal[indice + 3] = normalOut.x;
normal[indice + 4] = normalOut.y;
normal[indice + 5] = normalOut.z;

将计算出的法线存储在 normal 数组中。对于每个顶点，先存储当前顶点的法线，然后使用变形后的顶点位置再次调用 GerstnerWave_float 计算更新后的法线。

通过这些步骤，我们可以为每个顶点计算波浪效应，使得水面的动态效果更加真实。

绘制水面

通过将网格划分为多个三角形，使用纹理和法线来实现更真实的水面效果。总体流程：

1. 启用纹理和颜色设置：使用glEnable(GL_TEXTURE_2D)启用纹理，glColor4f设置颜色。
2. 遍历网格顶点：使用双重循环遍历网格。
3. 计算顶点索引：计算每个quad的两个三角形的顶点索引。
4. 设置顶点属性：使用glTexCoord2f、glNormal3fv和glVertex3fv分别设置纹理坐标、法线和顶点位置。
5. 结束绘制：使用glEnd结束三角形绘制。

启用纹理和设置颜色：

glEnable(GL_TEXTURE_2D);
glColor4f(0.0f, 0.8f, 1.0f, 0.8f);

启用2D纹理，并设置水面的颜色（蓝绿色，带有透明度）。

开始绘制三角形：

glBegin(GL_TRIANGLES);
for (j = 0; j < RESOLUTION-1; j++) {
    for (i = 0; i < RESOLUTION-1; i++) {
        // Calculate indices for the two triangles forming a quad
        indice = 6 * (i + j * (RESOLUTION + 1));
        unsigned int next_i = (i + 1) % (RESOLUTION + 1);
        unsigned int next_j = (j + 1) % (RESOLUTION + 1);
        unsigned int indice_next_i = 6 * (next_i + j * (RESOLUTION + 1));
        unsigned int indice_next_j = 6 * (i + next_j * (RESOLUTION + 1));
        unsigned int indice_next_ij = 6 * (next_i + next_j * (RESOLUTION + 1));

开始绘制三角形，遍历整个网格，将每个quad（四边形）拆分为两个三角形。计算这些三角形的顶点索引。

绘制第一个三角形：

        // First triangle
        // Vertices
        glTexCoord2f(i / (float)RESOLUTION, j / (float)RESOLUTION);
        glNormal3fv(&(normal[indice]));
        glVertex3fv(&(surface[indice]));

        glTexCoord2f((i + 1) / (float)RESOLUTION, j / (float)RESOLUTION);
        glNormal3fv(&(normal[indice_next_i]));
        glVertex3fv(&(surface[indice_next_i]));

        glTexCoord2f(i / (float)RESOLUTION, (j + 1) / (float)RESOLUTION);
        glNormal3fv(&(normal[indice_next_j]));
        glVertex3fv(&(surface[indice_next_j]));

设置第一个三角形的顶点。每个顶点包含纹理坐标、法线向量和位置：

1. glTexCoord2f 设置纹理坐标。
2. glNormal3fv 设置顶点法线。
3. glVertex3fv 设置顶点位置。

绘制第二个三角形：

        // Second triangle
        // Vertices
        glTexCoord2f((i + 1) / (float)RESOLUTION, j / (float)RESOLUTION);
        glNormal3fv(&(normal[indice_next_i]));
        glVertex3fv(&(surface[indice_next_i]));

        glTexCoord2f((i + 1) / (float)RESOLUTION, (j + 1) / (float)RESOLUTION);
        glNormal3fv(&(normal[indice_next_ij]));
        glVertex3fv(&(surface[indice_next_ij]));

        glTexCoord2f(i / (float)RESOLUTION, (j + 1) / (float)RESOLUTION);
        glNormal3fv(&(normal[indice_next_j]));
        glVertex3fv(&(surface[indice_next_j]));
    }
}
glEnd();

设置第二个三角形的顶点。与第一个三角形相同，每个顶点包含纹理坐标、法线向量和位置。

通过这些步骤，我们可以将Gerstner Wave模型计算的顶点变形和法线应用到OpenGL的绘制过程中，从而实现动态的水面效果。

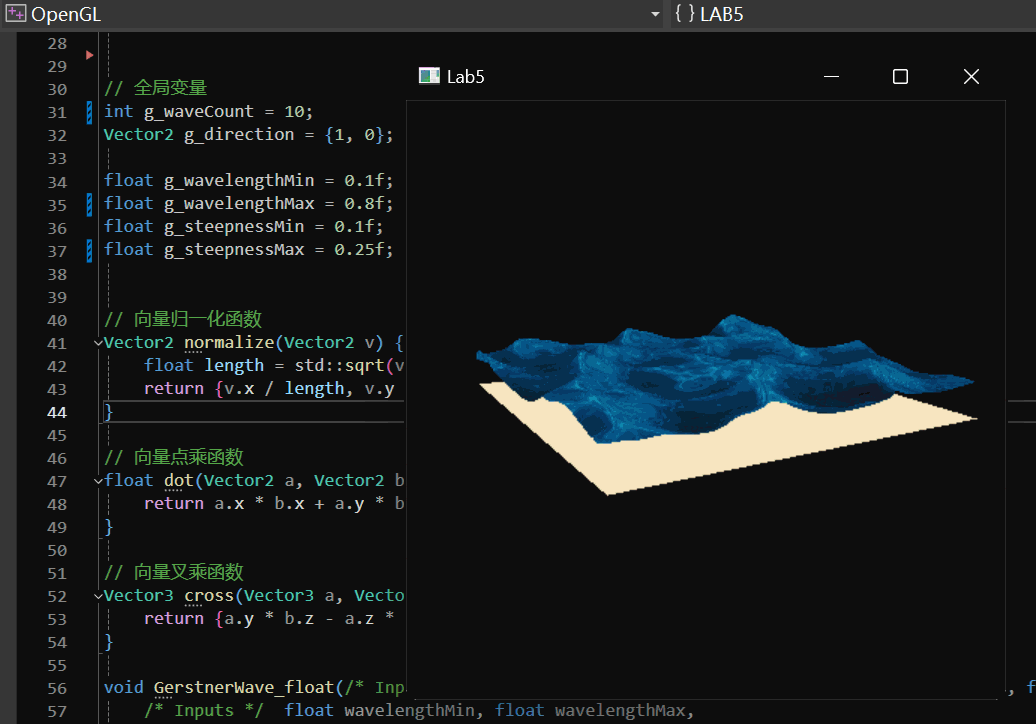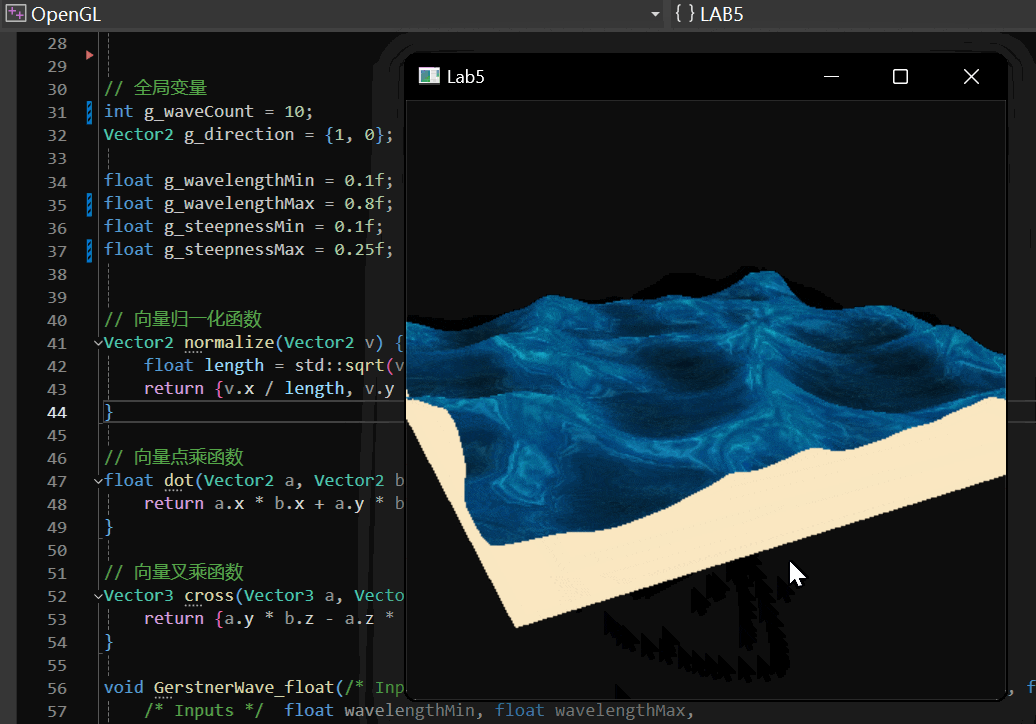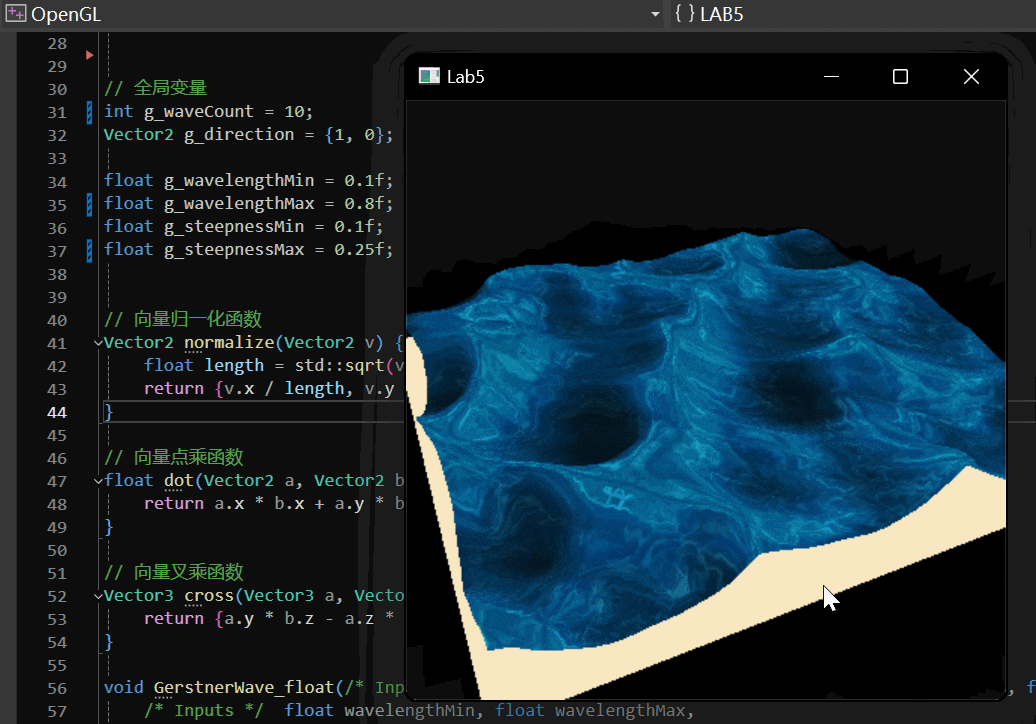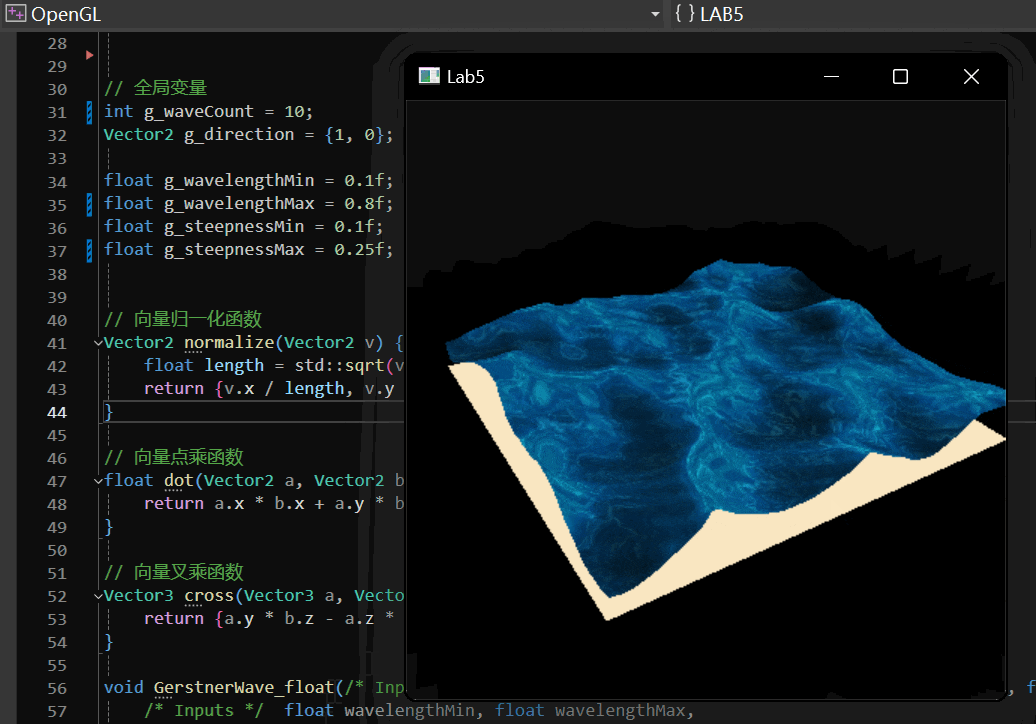
2.5.3 实现效果

实现效果如下：