1. ocam模型
可以参考我的另一篇博客ocam模型。
这里简单提一下ocam模型:
这个模型将中心折反射相机和鱼眼相机统一在一个通用模型下,也称为泰勒模型。它由Scaramuzza等人在2006年开发,其优点是折反射相机和屈光相机都可以用同一个模型来描述,即一个泰勒多项式。

公式:


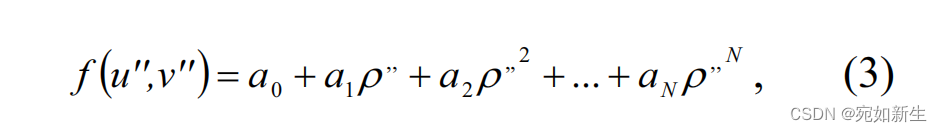
从上面一系列的公式可以看出,在相机标定成功的情况下,如果我们知道了图像平面上一点的像素,我们可以反投影出一个相机光心指向世界点的方向向量。至于那个
λ
\lambda
λ,我们反投影后做一个归一化即可。
源码:
function M=cam2world(m, ocam_model)
n_points = size(m,2);
ss = ocam_model.ss; % 多项式系数
xc = ocam_model.xc; % 主点
yc = ocam_model.yc; % 主点
width = ocam_model.width;
height = ocam_model.height;
c = ocam_model.c;
d = ocam_model.d;
e = ocam_model.e;
A = [c,d;
e,1];
T = [xc;yc]*ones(1,n_points);
m = A^-1*(m-T); % 图像平面到归一化平面
M = getpoint(ss,m); % 反投影过程
M = normc(M); % normalizes coordinates so that they have unit length (projection onto the unit sphere)
function w=getpoint(ss,m)
% Given an image point it returns the 3D coordinates of its correspondent optical
% ray
w = [m(1,:) ; m(2,:) ; polyval(ss(end:-1:1),sqrt(m(1,:).^2+m(2,:).^2)) ];
2. 消影点
消影点:几何上一条世界直线的消影点由平行于该直线并过相机光心,然后与成像平面的交点。消影点只依赖世界直线的方向,与其位置无关,如果这条直线与成像平面平行,则其消影点位于图像的无穷远处。

如何求解一条直线的消影点?一组平行线即可确定。如下图:
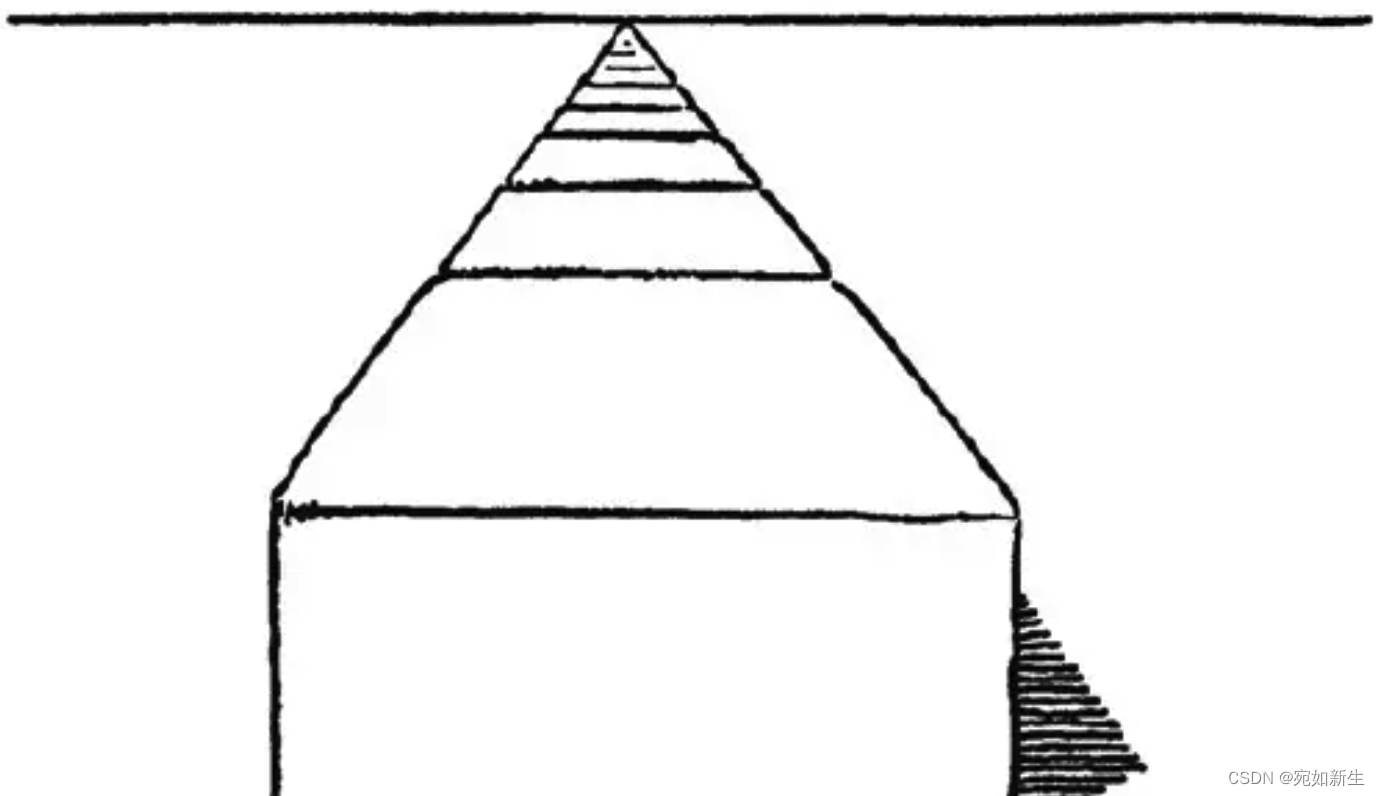
真实世界中的两条平行线在图像中会交于一点,那就是消失点,也就是说我们通过两条平行线就可以确定消失点。
3. 基于消影点进行相机主点标定


上面第一幅图是棋盘格在相机图像平面上的成像。可见由于棋盘格天然由好几组平行线,比如横向和纵向两组,就可以确定两个消失点。又根据第二幅图,过相机光心和消失点的直线是与世界直线平行的,所以我们可以通过棋盘格得到两条过相机光心和两个消失点的方向向量,这两个向量垂直。利用这个关系可以进行相机内参(主点)的标定。
3.1 基于ocam模型的主点标定
原理如前面所述,通过棋盘格中天然存在的几组垂直关系的平行线可以确定多组互相垂直的(相机光心到消失点)的方向向量,然后构建误差方程(垂直关系的方向向量点积为0)。

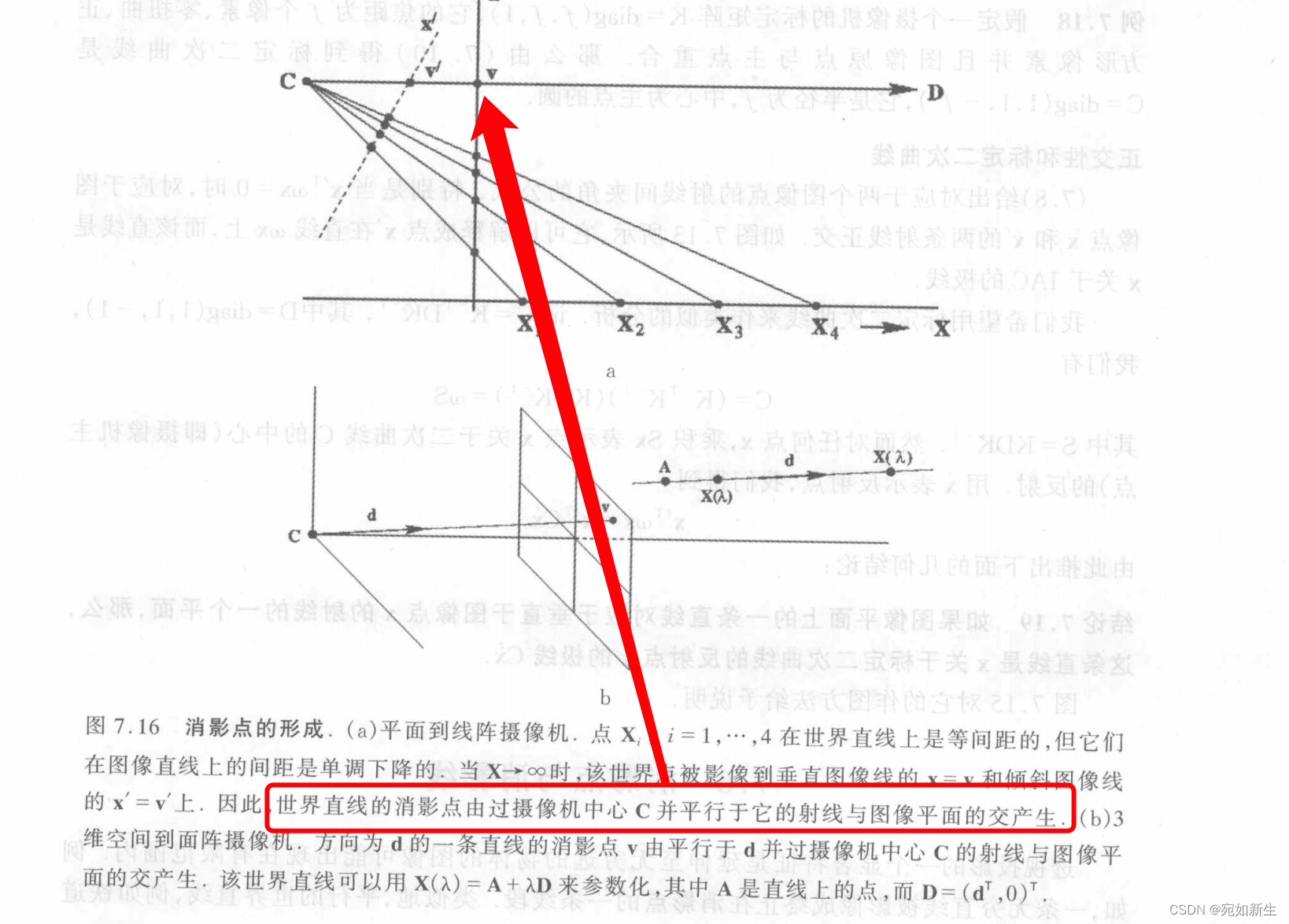
误差函数中因为包含了反投影过程,所以包含了优化变量相机主点。(这里我已经知道了ocam相机除主点外其他的参数。)


























 864
864

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










