ARIMA预测销量

最新推荐文章于 2024-12-25 18:40:58 发布

Westbroobo

最新推荐文章于 2024-12-25 18:40:58 发布

阅读量1.6k

点赞数 4

文章标签：机器学习人工智能数据挖掘

本文链接：https://blog.csdn.net/Westbrook_bo/article/details/129302617

版权

文章介绍了如何使用ARIMA模型对时间序列数据进行分析和预测，包括数据预处理、模型定阶、参数估计、模型检验等步骤，以茶叶市场销量为例，展示了从数据获取到模型预测的全过程，强调了平稳性检测和自相关图、偏自相关图在模型选择中的作用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

提要

在茶叶市场分析案例中提到过过于时间序列做销量预测，这里上传相关数据，通过ARIMA模型对销量进行预测，对时间序列进行介绍和使用
案例链接：https://blog.csdn.net/Westbrook_bo/article/details/129297787?spm=1001.2014.3001.5501
相关数据：在这里插入图片描述

、

一、时间序列模型

（一）简介

时间序列分析是根据系统观测得到的时间序列数据，通过曲线拟合和参数估计来建立数学模型的理论和方法。它一般采用曲线拟合和参数估计方法（如非线性最小二乘法）进行，常用在国民经济宏观控制、区域综合发展规划、企业经营管理、市场潜量预测、气象预报、水文预报、地震前兆预报、农作物病虫灾害预报、环境污染控制、生态平衡、天文学和海洋学等方面。

（二）方法

要解决一个时间序列问题来预测未来数据，可以有多种方法：朴素法、简单平均法、移动平均法、简单指数平滑法、霍尔特线性趋势法、Holt-Winters季节性预测模型、自回归移动平均模型（ARIMA）。这里以ARIMA模型为例，解决企业销量数据的时间序列问题。

（三）自回归移动平均模型（ARIMA）的基本步骤

1.观测数据获取与预处理

通过特定方式获取观测数据后，需判断是否为平稳时间序列，对于非平稳时间序列要先进行d阶差分运算化为平稳时间序列。

2.模型定阶

要对平稳时间序列分别求得其自相关系数ACF 和偏自相关系数PACF ，通过对自相关图和偏自相关图的分析，得到最佳的阶层p和阶数q，结合差分阶数d确定模型。

3.参数估计

对模型的参数进行估计的方法通常有相关矩估计法、最小二乘估计以及极大似然估计等。

4.模型检验

模型的验证主要是验证模型的拟合效果，如果模型完全或者基本解释了系统数据的相关性，那么模型的噪声序列为白噪声序列，那么模型的验证也就是噪声序列的独立性检验。

二、ARIMA模型建立

（一）获取数据并绘制时间序列图

读取文件中的销量数据并绘制时间序列图，代码如下。

import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = ['Arial Unicode MS', 'Microsoft Yahei', 'SimHei', 'sans-serif']
plt.rcParams['axes.unicode_minus'] = False
data = pd.read_excel('.\销量数据（按月份）.xlsx',index_col=0)
data.plot(title="2018年-2022年销量数据图")
plt.show()

得到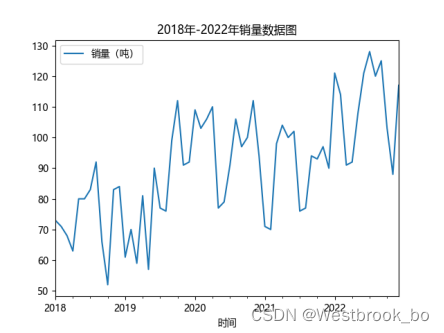： Alt

（二）平稳性检测

通过平稳性检测判断是否为平稳时间序列，若p值小于或等于0.05，则为平稳时间序列，反之则为非平稳时间序列，此处恰好为平稳时间序列，不再进行差分计算，d的值为0。

# 代码
from statsmodels.tsa.stattools import adfuller as ADF
a = ADF(data)
print('ADF检验结果为：', a)
print('p值为：',a[1])
if a[1] <= 0.05:
    print('经判断该时间序列为平稳时间序列')
else:
    print('经判断该时平稳时间序列，需进行差分计算')

输出结果：
ADF检验结果为： (-3.5795382624570413, 0.006164479167700151, 0, 59, {'1%': -3.5463945337644063, '5%': -2.911939409384601, '10%': -2.5936515282964665}, 396.37716780293573)
p值为： 0.006164479167700151
经判断该时间序列为平稳时间序列

（三）绘制自相关图和偏自相关图

对已获得的平稳序列，绘制自相关图和偏自相关图，选择合适的p，q值。

from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.graphics.tsaplots import plot_pacf
plot_acf(data)
plot_pacf(data)
plt.show()

得到自相关图和偏相关图：
Alt Alt

（四）模型定阶与选择

通过观察自相关图和偏自相关图，可以看出：自相关图显示滞后有4个阶超出了置信边界，偏相关图显示在滞后2阶时的偏自相关系数超出了置信边界，之后缩小至0。则有以下模型可以选择：
1.ARIMA(0,4) 模型：自相关图在滞后4阶之后缩小为0，且偏自相关缩小至0，是一个阶数q = 4的移动模型；
2.ARIMA(1，0)模型：偏自相关图在滞后1阶之后缩小为0，且自相关缩小至0，是一个阶数p = 1的自回归模型；
3.ARIMA(1,4)模型：使得自相关和偏自相关都缩小至0，是一个混合模型。
之后通过赤池信息准则和贝叶斯信息准则分别计算AIC、BIC和HQIC，选择最佳模型。

import statsmodels.api as sm
arima_mod04 = sm.tsa.ARIMA(data,order=(0,0,4)).fit()
print(arima_mod04.aic,arima_mod04.bic,arima_mod04.hqic)
arima_mod10 = sm.tsa.ARIMA(data,order=(1,0,0)).fit()
print(arima_mod10.aic,arima_mod10.bic,arima_mod10.hqic)
arima_mod14 = sm.tsa.ARIMA(data,order=(1,0,4)).fit()
print(arima_mod14.aic,arima_mod14.bic,arima_mod14.hqic)

输出结果
502.06518113575 514.6312485090825 506.98046089289744
496.25380643135645 502.5368401180227 498.7114463099302
497.49107869387035 512.1514906294251 503.22557174387566

可以看到ARIMA(1,0)的AIC、BIC和HQIC均最小，因此是最佳模型。

（五）模型检验

1.残差QQ图

这里使用残差QQ图，它用于直观验证一组数据是否来自某个分布，或者验证某两组数据是否来自同一（族）分布。

from statsmodels.graphics.api import qqplot
resid = arima_mod10.resid
plt.figure(figsize=(12,8))
qqplot(resid, line='q', fit=True)
plt.show()

Alt

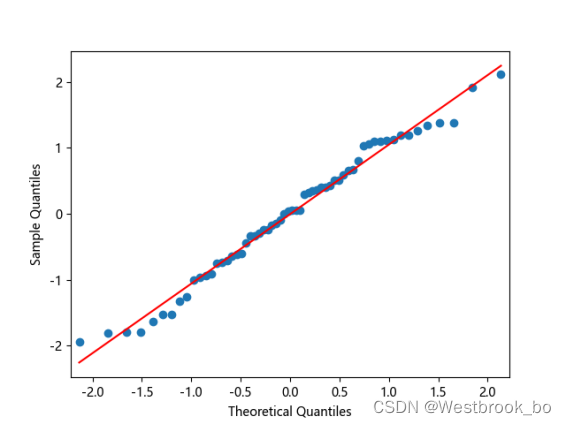
2.残差自相关检验

对ARIMA(1,0)模型所产生的残差做自相关图,代码如下。

fig = plt.figure(figsize=(12,8))
ax1 = fig.add_subplot(211)
fig = sm.graphics.tsa.plot_acf(arima_mod10.resid.values.squeeze(), lags=10, ax=ax1)
ax2 = fig.add_subplot(212)
fig = sm.graphics.tsa.plot_pacf(arima_mod10.resid, lags=10, ax=ax2)
plt.show()

Alt

3.D-W检验

德宾-沃森检验，简称D-W检验，是目前检验自相关性最常用的方法，但它只使用于检验一阶自相关性。当DW值显著的接近于O或４时，则存在自相关性，而接近于２时，则不存在（一阶）自相关性。这样只要知道DW统计量的概率分布，在给定的显著水平下，根据临界值的位置就可以对原假设进行检验。

print(sm.stats.durbin_watson(arima_mod10.resid.values))

输出结果
1.92800760817413

结果明显接近于2，说明不存在自相关性。

4.Ljung-Box检验

Ljung-Box检验是对随机性的检验,或者说是对时间序列是否存在滞后相关的一种统计检验。对于滞后相关的检验，我们常常采用的方法还包括计算ACF和PCAF并观察其图像，但是无论是ACF还是PACF都仅仅考虑是否存在某一特定滞后阶数的相关。LB检验则是基于一系列滞后阶数，判断序列总体的相关性或者说随机性是否存在。
时间序列中一个最基本的模型就是高斯白噪声序列。而对于ARIMA模型，其残差被假定为高斯白噪声序列，所以当我们用ARIMA模型去拟合数据时，拟合后我们要对残差的估计序列进行LB检验，判断其是否是高斯白噪声，如果不是，那么就说明ARIMA模型也许并不是一个适合样本的模型。

import numpy as np
r,q,p = sm.tsa.acf(resid.values.squeeze(), qstat=True)
datap = np.c_[range(1,18), r[1:], q, p]
table = pd.DataFrame(datap, columns=['lag', "AC", "Q", "Prob(>Q)"])
print(table.set_index('lag'))

输出结果
            AC          Q  Prob(>Q)
lag                                
1.0  -0.008204   0.004244  0.948058
2.0  -0.126766   1.034917  0.596034
3.0   0.086742   1.525963  0.676291
4.0   0.105707   2.268235  0.686558
5.0   0.014319   2.282103  0.808892
6.0   0.115141   3.195396  0.783953
7.0   0.237746   7.162692  0.412139
8.0   0.053315   7.366036  0.497703
9.0  -0.069297   7.716307  0.562969
10.0  0.127112   8.918428  0.539862
11.0 -0.017123   8.940686  0.627367
12.0 -0.210953  12.389533  0.414924
13.0  0.037791  12.502572  0.486925
14.0  0.281337  18.903434  0.168672
15.0 -0.010634  18.912782  0.217713
16.0 -0.053267  19.152673  0.260826
17.0 -0.046662  19.341037  0.309312

检验的结果就是看最后一列前十二行的检验概率（一般观察滞后1～12阶），如果检验概率小于给定的显著性水平就拒绝原假设，其原假设是相关系数为零。就结果来看，若取显著性水平为0.05，那么相关系数与0没有显著差异，即为白噪声序列。

（六）模型预测

模型确定之后，就可以开始进行预测了，我们对未来两年红24个月的数据进行预测，并绘制图形，代码如下。

predict_sunspots = arima_mod10.predict('2023-01', '2024-12', dynamic=True)
fig, ax = plt.subplots(figsize=(12, 8))
print(predict_sunspots)
ax = data.iloc[0:].plot(ax=ax)
predict_sunspots.plot(ax=ax)
plt.show()

输出结果
2023-01-01    107.150228
2023-02-01    101.025465
2023-03-01     97.216980
2023-04-01     94.848796
2023-05-01     93.376217
2023-06-01     92.460542
2023-07-01     91.891158
2023-08-01     91.537106
2023-09-01     91.316950
2023-10-01     91.180053
2023-11-01     91.094928
2023-12-01     91.041995
2024-01-01     91.009081
2024-02-01     90.988615
2024-03-01     90.975888
2024-04-01     90.967975
2024-05-01     90.963054
2024-06-01     90.959994
2024-07-01     90.958091
2024-08-01     90.956908
2024-09-01     90.956172
2024-10-01     90.955715
2024-11-01     90.955431
2024-12-01     90.955254