Profile
四大生成模型之一的
GAN由一对生成器G和鉴别器D构成。
以图像生成为 🌰,GAN的训练有两个特点:☝ 在缺乏其他限制下,生成的图像的分布严格近似于D看到的真实图像分布;✌ 对于生成模型,过拟合(over fitting只能复现训练时见过的样本)优于欠拟合(under fitting,训练炸了,无法生成自然的图像)。
G过拟合的发生比较少;G欠拟合是更常见的——其表现为:
- 以
LSGAN为 🌰,鉴别器D对生成样本的评分很低,即 D f a k e → 0 D_{fake}\rightarrow0 Dfake→0,而对真实的训练样本的评分很高,即 D r e a l → 1 D_{real}\rightarrow1 Dreal→1;G生成的样本愈发诡异。纠其原因是:
D太强,G太弱 →D轻易记住了所有真实样本,只要不是真实样本,那么就直接判定为False- 因此一个可能的直接原因就是:用于训练的真实样本太少,
D记住了- 其他原因包含但不限于:
- ☝
G的网络结构决定的G的 Capacity 相对较弱,D的网络结构决定的D的 Capacity 相对强很多;- ✌ 这个任务太难了 😞
上述阐述的是
G的欠拟合,相对于D就是过拟合了。
这篇文章正是解决少样本训练
GAN的时候,D容易过拟合、G完全不够打的问题。
核心思想是数据增强,是的!就是在 Classification, Detection 等 Down-streaming 任务中经常用的数据预处理。这么直接的方法为什么前人没想到?o O ~ 不是没想到,而是考虑到,🤔GAN的第一个特点,如果使用增强样本直接训练,这些增强的变换直接改变了原训练样本所代表的目标分布,这必然使得G生成的样本分布也偏离了;文章将其称为 L e a k i n g Leaking Leaking,即“渗透”。
- 举个直接的例子,引入噪声算是最常见的数据增强了吧!那么这会直接导致训练完毕的
G生成的样本也带有噪声。而所谓 “分布的改变” 的数学体现,在本文中就是生成样本集与真实训练样本集之间的 F I D FID FID 分数变大了。
1. Introduction
主要内容:
- 本文展示了如何运用一系列的数据增强( D A / D a t a A u g m e n t a t i o n \rm DA/Data Augmentation DA/DataAugmentation)来防止
D过拟合,同时- 保证没有任何增强变换被渗透到生成图像中。
一些说明:
- “少样本”的“少”在本文中可以是 1 k , 2 k , 5 k , 10 k , e t c \rm 1k, 2k, 5k, 10k, etc 1k,2k,5k,10k,etc,这是对于
BigGAN、StyleGAN-v2而言的;具体的“多少”视任务难度、分辨率、模型性能(Capacity)等决定;- 本文的理论支撑并不充分,更多的是一些训练
GAN的技巧分享;期待深刻数学理论的 dalao 请自行斟酌食用。
2. GAN 中的过拟合
我们首先研究一下训练数据的数量是如何影响
GAN训练的。
实验 1 细节:将大规模数据集(如FFHQ,LSUN CAT)按随机顺序、随机划分为子集;随机初始化网络;图像分辨率为 256 × 256 256\times256 256×256;测试的时候,G随机生成 50 k \rm 50k 50k 个样本,然后与所有可用的训练样本计算 F I D \rm FID FID 分数。
实验1 结果:
| F i g . 1 \rm Fig.~1 Fig. 1 | 说明 |
|---|---|
 | 1️⃣ 横轴表示训练进程,纵轴指示
F
I
D
\rm FID
FID 分数; 2️⃣ 不同样本数量下, G 的出发点是相同的,但越往后差别越大;3️⃣ 训练样本数足够多, G 最终收敛到很低的
F
I
D
\rm FID
FID;4️⃣ 训练样本数不够, G 在中间反弹;且数据越不足,反弹发生得越早。❗️❗️ 图中黑色的点对应每种情况下的训练进程。 |
 | 1️⃣ 横轴是训练进程,纵轴是 D 对输入样本的输出得分(分布);蓝色针对真实样本,橙色针对真实生成样本;2️⃣ 实线表示分数的分布的均值;红色竖虚线确定了 D 完全过拟合的时间点;3️⃣ 对应图 (a) 的 20 k \rm 20k 20k 和 50 k \rm 50k 50k 的折现,黑色的点大约分别出现在 3 M \rm 3M 3M 和 12 M \rm 12M 12M 的位置; 4️⃣ 注意!这个实验结果传达了一个重要的信息:过拟合出现的时间与 F I D \rm FID FID 开始反弹似乎是强烈对应的;即, F I D \rm FID FID 反弹似乎可以作为过拟合的信号。 |
2.1 随机 D 增强(
S
D
A
/
S
t
o
c
h
a
s
t
i
c
D
i
s
c
r
i
m
i
n
a
t
o
r
A
u
g
m
e
n
t
a
t
i
o
n
\rm SDA/Stochastic Discriminator Augmentation
SDA/StochasticDiscriminatorAugmentation)
上面我们已经了解了,数据量不够时训练
GAN会发生什么事;在理解为什么D增强能防止D过拟合之前,我们有必要了解什么是D增强(鉴别器增强)。
所谓D增强就是将喂入D的部分或全部样本(包括训练用真实样本和G生成伪样本)先作数据增强的预处理。
一个经典的工作是 b C R \rm bCR bCR,模型结构如下:
| 结构( F i g 2 ( a ) \rm Fig 2(a) Fig2(a)) | 说明 |
|---|---|
 | 1️⃣ 虚线左边是训练 G 的时候,右边是训练 D 的时候;2️⃣ 相较于一般的 GAN,在于增加了输入 D 的样本分别经过
A
u
g
\rm Aug
Aug 的支路;3️⃣ 其基本思想是:两种不同的增强方式作用到同一张图像上, D 应当给出同样的评分;4️⃣ 这就是右图蓝色部分 ( x − y ) 2 (x-y)^2 (x−y)2 表征的 “ C R / C o n s i s t e n c y R e g u l a r i z a t i o n \rm CR/Consistency~Regularization CR/Consistency Regularization”; 5️⃣ 训练 G 时不引入
C
R
\rm CR
CR 的原因就是为了防止数据增强变换的渗透;看样子好像不会渗透?🙂6️⃣ 文中引入 C R \rm CR CR 的 insight 是: D 本质上是一个分类器,数据增强提高 D 的鲁棒性(;因此可以提高博弈的质量,进而提高 G 的性能);7️⃣ 但这同时也导致了渗透( L e a k i n g \rm Leaking Leaking)的风险,因为: ① 尽管 D 抑制 G 的生成(正常样本),由于
C
R
\rm CR
CR 抑制 G 生成增强后的样本(必要性),但对抗/博弈天然允许 G 仿真真实正常样本分布的同时也仿真增强后的样本的分布;② D l o s s \rm D~loss D loss 抑制的是隐编码,抑制必要条件并不一定严格抑制作为充分条件的输入图像本身。 |
2.2 设计不发生“渗透”的增强方法
我们可以先预览本文的框架结构如下表,
| 结构( F i g . 2 ( b ) \rm Fig.~2(b) Fig. 2(b)) | 说明 |
|---|---|
 | 1️⃣ 与上图
6
(
a
)
\rm 6(a)
6(a) 相比,不使用
C
R
CR
CR 正则项; 2️⃣ 训练 D 时喂给 D 的全部样本都经过数据增强;3️⃣ 训练 G 时喂给 D 的样本也全部经过增强.4️⃣ 这背后的思想是:当 D 看过的所有真实样本和生成样本都是经过增强后的新的分布时,G 为了使生成的样本经过“同样的”增强后匹配到“同样的”增强后的真实数据分布,一个方法就是保证生成的样本分布在增强之前匹配增强之前的真实样本分布。 5️⃣ 注意这里的“同样的”并不是针对每个样本都用同一个固定的增强操作,而是对整个样本分布而言的,包括真实样本分布与生成伪样本分布. |
但上面 4️⃣ 提到的思想并不具有充分性,即:
- 生成伪样本分布 x ∼ G ( x ) x \sim G(x) x∼G(x) M A T C H E S \bf MATCHES MATCHES 真实样本分布 x ∼ X x \sim \mathcal X x∼X ⟹ 增强后的生成伪样本分布 A u g ( x ) ∼ A u g ( G ( x ) ) {\rm Aug}(x) \sim {\rm Aug}(G(x)) Aug(x)∼Aug(G(x)) M A T C H E S \bf MATCHES MATCHES 增强后真实样本分布 A u g ( x ) ∼ A u g ( X ) {\rm Aug}(x) \sim \mathcal {\rm Aug}(X) Aug(x)∼Aug(X)
但反过来是不一定成立的。除非,增强 A u g \rm Aug Aug 是可逆的,在本文中称之为可撤销的( U n d o a b l e \bf Undoable Undoable).
因为这样一来,构造了样本在某种层面上的成对的对应关系。
同样,这里讲的 “ A u g \rm Aug Aug 可撤销” 也是对样本集所代表的的数据分布层面上而言。
下面我们阐述论文对 N o n l e a k i n g A u g \rm Non~leaking~Aug Non leaking Aug 的设计思路。(😅这应该是本文唯一的理论支撑)
D增强对应着将扭曲引入D,甚至是破坏性地“给D戴上了护目镜”,从而D无法看到干净的样本分布(不得不说老外的比喻总是恰到好处👍)。
B o r a e t a l {\rm Bora}~et~al Bora et al 发现:在这种情况下,只要这种数据退化,在概率分布的层面上对数据空间是由可逆的变换表示,GAN的训练就可以隐式地撤销这些退化、找到原干净的真实样本分布作为匹配目标。
这里关键🔑的一点是:"It is crucial to understand that this does not mean that augmentations performed on individual images would need to be undoable."即前面我们反复强调的 A u g \rm Aug Aug 操作可逆或者可撤销是在数据分布层面上,并不指针对单个图像样本。
作者这里给出了几个🌰,
| Example | 是否是 non-leaking 的 A u g \rm Aug Aug | 解释 |
|---|---|---|
| 任意图像样本有 90 % 90\% 90% 的时间被置零 | ✅ | 对于人类而言,只需要忽略 90 % 90\% 90% 时间内见到的黑色图像,仅关注 10 % 10\% 10% 的时间内见到的正常图像,推理出原数据分布是可以做到的。 |
| 对图像作均匀的随机的 { 0 ° , 90 ° , 180 ° , 270 ° } \{0\degree, 90\degree, 180\degree, 270\degree\} {0°,90°,180°,270°} 旋转 | ❎ | 注意这里强调“均匀”,对于人类而言,仅凭借这些样本,无法判断哪一种 O r i e n t a t i o n \rm Orientation Orientation 是需要的。 |
| 对图像以概率 p < 1 p<1 p<1 的随机作 { 0 ° , 90 ° , 180 ° , 270 ° } \{0\degree, 90\degree, 180\degree, 270\degree\} {0°,90°,180°,270°} 旋转 | ✅ | 如此增加了定向为
0
°
0\degree
0° 的图像的相对出现的比重,因此我们可以很大信心认为该定向即目标定向。 现在增强样本的分布当且仅当 G 生成的干净样本的分布是正确的定向的时候,增强生成样本分布于增强真实样本分布才可以匹配到。 |
与人类认知方式的联系是:对于人类而言,只需要看到少量干净的目标样本,随后接收任何被处理过的样本,人类都能够推理出其背后的干净的样本。
Nice! 现在,只要确保 A u g \rm Aug Aug 被以 p < 1 p<1 p<1 的概率执行,且采用 F i g . 2 ( b ) {\rm Fig. 2}(b) Fig.2(b) 的框架训练GAN,就可以实现少量样本下训练GAN且D不拟合了。
这里我们还可以再总结一下一系列常用的数据增强方式:
- 确定性映射(Deterministic Mapping),如:基础变换(Basis Transformation)
- 额外噪声(Additive Noise)
- 变换组(Transformation Groups),如:图像或颜色空间的旋转、翻转和缩放(Image or Color Space Rotations, Flips, & Scaling)
- 投影(Projection),如:Cutout
- p . s . \rm p.s. p.s. Non-leaking 的数据增强方式按某个固定顺序组合的整个增强操作也是非渗透的。
现在我们来看第 2 个实验,
| F i g . 3 \rm Fig.~3 Fig. 3 | |
|---|---|
 | 1️⃣ Isotropic Image Scaling with log-normal distribution 是一种概率无关的、安全的、非渗透的数据增强方式; 2️⃣ 也就是等比例缩放啦,不过后面的 with log-normal distribution 就不了解,懂得的读者可以评论区分享一下,不胜感激🙏🏻 ; 3️⃣ 猜测应该是使用全部数据训练的 GAN,不然
F
I
D
\rm FID
FID 不可能这么低;4️⃣ 上面的组图表示下边的散点图对应的实验, GAN 生成的样本示例;5️⃣ 蓝色的色带是对应每个点的高斯晕染的混合,只是辅助观察趋势而已; 6️⃣ 这是一个白板试验,用于与下面 ( b ) ( c ) (b)(c) (b)(c) 对比。 |
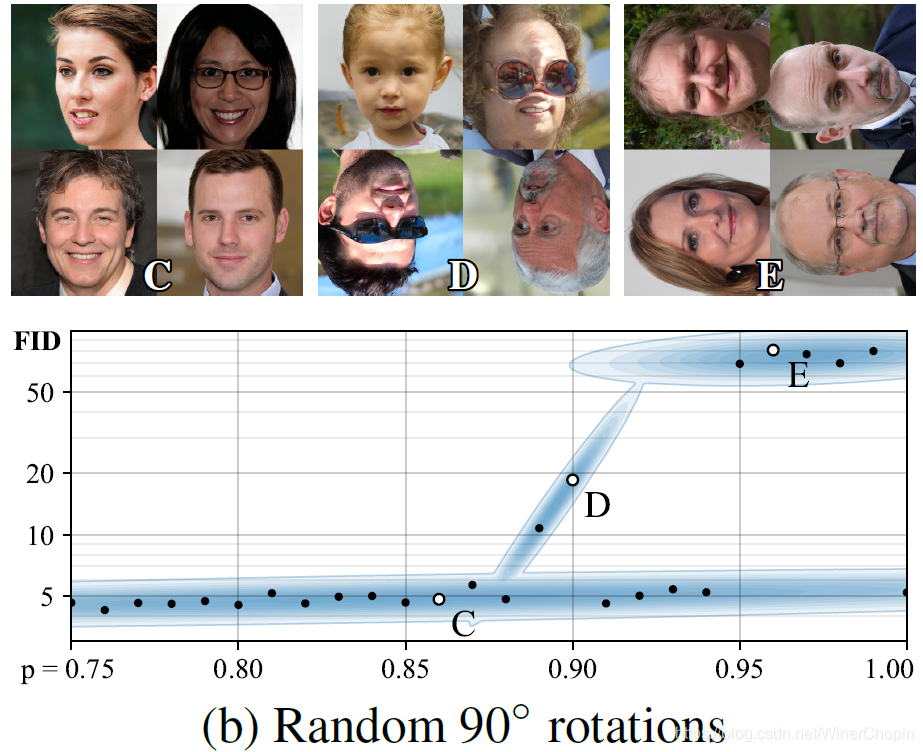 | 1️⃣ 以概率
p
<
1
p<1
p<1 旋转图像
90
°
90\degree
90° 的正整数倍 作为
A
u
g
\rm Aug
Aug 方式; 2️⃣ 可以发现,当概率 p p p 超过某个值之后,训练的 GAN 的 FID 急速增加,对应 G 生成的样本中出现了
0
°
0\degree
0° 以外定向的图像;3️⃣ 这是因为现在 G 生成的干净样本分布被
A
u
g
\rm Aug
Aug 渗透了,生成了一些异常定向的人脸图像,而计算
F
I
D
\rm FID
FID 的真实样本可都是
0
°
0\degree
0° 定向的,
F
I
D
\rm FID
FID 肯定暴增! 4️⃣ 值得注意的是,当 p = 1.0 p=1.0 p=1.0 的时候,这种渗透又必定不会发生, 因为这样的话,喂给 D 的样本一定是经过顺时针旋转
90
°
90\degree
90°、逆时针旋转
90
°
90\degree
90° 或者旋转
180
°
180\degree
180° 的,即 D 未曾见过正常定向的人脸,那么 G 只有生成的都是正常定向的人脸才可以保证增强后生成样本分布匹配增强后真实样本分布。设想一下,如果允许 G 生成逆时针旋转
90
°
90\degree
90° 的人脸,在百分之百发生旋转的增强中,总会因为顺时针旋转
90
°
90\degree
90° 导致喂给 D 的样本存在正常定向人脸,这就与增强后的真实样本分布不符合了。对于其他两种旋转情况也是一样的。🆙这点不重要,但是是一个事实 ❗️❗️ |
 | 1️⃣ 同样的渗透也发生在:当以连续的颜色增强作为
A
u
g
\rm Aug
Aug 操作时,当
p
p
p 过大的时候; 2️⃣ 作者在这里分析: 当 p p p 过高时, G 无法判断增强后的样本还是干净样本才是被期望的,具体的,个人猜测,是因为p p p 偏高使得增强后的样本分布内,不同的增强样本子分布之间可以通过同样的 A u g \rm Aug Aug 相互转换得到,从而允许 G 也模仿、生成增强后的真实样本。 |
诶,到这里,本文最让人惊呼的时候来了!
作者突然总结:从上面的实验 ( b ) ( c ) (b)(c) (b)(c) 看出,在实际应用中,只要 p < 0.8 p<0.8 p<0.8,那么增强D的时候渗透不会发生 。
好咯👌🏼,就当是训练的一个 trick 咯!
作者将这个 p = 0.8 p=0.8 p=0.8 的阈值称为 T h e P r a t i c a l S a f e t y L i m i t The~Pratical~Safety~Limit The Pratical Safety Limit(实际安全限制)😅
至此,关于如何在少数据情况下训练
GAN的方法就介绍结束了,下面两部分围绕设计数据增强流水线,和一个动态调节 p p p 的更好的方法。
2.3 我们的增强流水线( A u g m e n t a t i o n P i p e l i n e \rm Augmentation~Pipeline Augmentation Pipeline)
我们不妨先假设,尽可能多样的数据增强集合是有利的。
作者先考虑 18 18 18 中增强方式,划分为 6 6 6 组:
- Pixel Blitting,包括:水平翻转( x x x-flips),上文提到的正整数倍的 90 ° 90\degree 90°旋转,和整数平移(Integer Translation)
- 更多一般的几何变换(Geometric Transformations)
- 颜色变换(Color Transform)
- 图像空间滤波(Image Filtering)
- 添加噪声(Additive Noise)
- Cutout
具体的实验设置:
- 预定义一个变换的集合,并固定各个变换之间的执行顺序
- 每个变换都有 p p p 的概率被执行, 1 − p 1-p 1−p 的概率被跳过;所有变换的 p p p 值是一样的,但是独立的;
- 当该流水线上有许多 A u g \rm Aug Aug 操作时,即使是很小的 p p p,全部都被跳过、喂给
D干净的样本的概率依旧是很低很低的
现在我们准备进入第 3 个实验——
| 实验 3( F i g . 4 \rm Fig.~4 Fig. 4) |
|---|
 |
1️⃣ 首先对比不同的数据量训练 GAN,不同类别(组别)的增强变换随着其被出发的概率不同而变化的情况;2️⃣ 灰色的水平虚线是不使用任何增强方式训练的 GAN 的性能;3️⃣ 可以看出,在前两种数据量不足的情况下,增强 D 是起作用的;但实际应用中并不是所有的 non-leaking 的增强都是其积极作用,且不同组别的增强操作的最佳增强强度
p
p
p 也是不同的,再者,同一组
A
u
g
\rm Aug
Aug 的最优
p
p
p 是与数据集大小相关的;4️⃣ 有些增强方式在 p p p 稍微大些后,甚至渗透到 G 的生成样本分布上;事实是,增强 D 在数据缺乏的情况下可以起到积极作用,但在数据充分甚至冗余的情况下,增强 D 只会带来学习的难度;从
(
a
)
(a)
(a) 个别组增强起消极作用,到
(
b
)
(b)
(b) 个别组增强的消极作用随着
p
p
p 越大而增长,到
(
c
)
(c)
(c) 中所有增强组都是有害的。!基于这个实验结果,第 2 个“Trick” 出现了:在下面的实验中,增强流水线上的操作就只包括 B l i t , G e m o , C o l o r \rm Blit,~Gemo,~Color Blit, Gemo, Color. |
另一个相对不是很重要的实验是:
| F i g . 4 ( d ) \rm Fig.~4(d) Fig. 4(d) | 说明 |
|---|---|
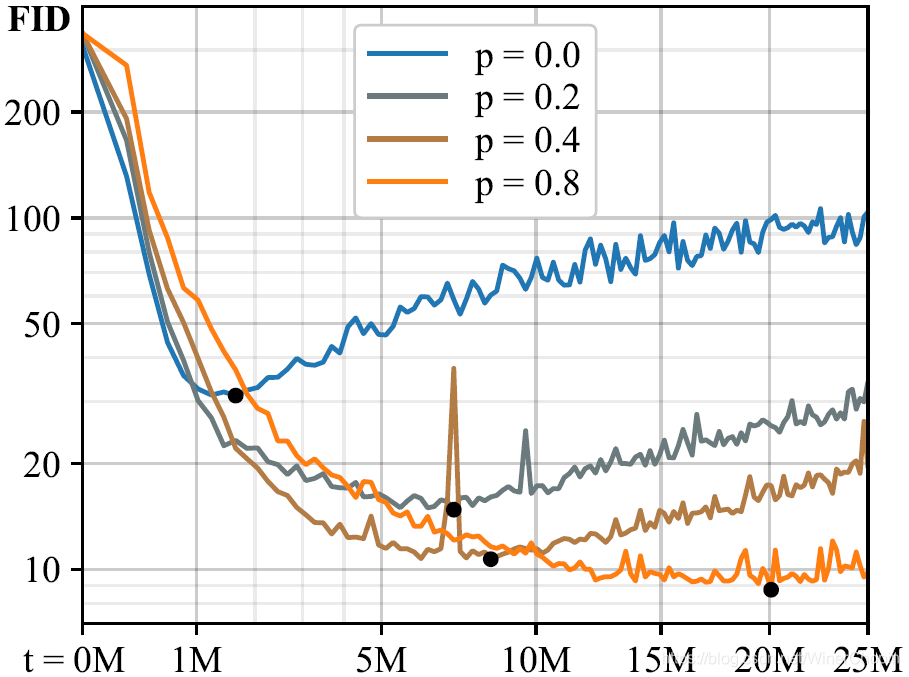 | 1️⃣ 训练数据量
10
K
10 \rm K
10K,使用的
A
u
g
\rm Aug
Aug 类别是
G
e
o
m
\rm Geom
Geom; 2️⃣ 曲线说明,增强 D 减缓 D 过拟合的同时,会使得收敛速度变慢。 |
3 自适应鉴别器增强( A D A : A d a p t i v e D i s c r i m i n a t o r A u g m e n t a t i o n \rm ADA:~Adaptive~Discriminator~Augmentation ADA: Adaptive Discriminator Augmentation)
实验 3 传达了一个重要的信息,就是: ( a ) ( b ) ( c ) (a)(b)(c) (a)(b)(c) 说明,最佳增强强度与训练数据的大小有关,那实际应用的时候,不同人不同用户不同数据集,如果通过网格搜索(数据集大小 × p \times p ×p),那是相当耗时的; ( d ) (d) (d) 说明在训练的不同阶段,固定强度的 A u g \rm Aug Aug 对防止过拟合起的作用是动态的。
这两个信息引出的一个问题是:自适应调整 p p p。
Q 1 \rm Q1 Q1: 根据什么调整 p p p?
A 1 \rm A1 A1:D过拟合了,调整 p p p 组织过拟合。
Q 2 \rm Q2 Q2: 那怎么判断D过拟合了?
A 2 \rm A2 A2:
- 还记得前面实验 1 的 F i g . 1 ( a ) {\rm Fig.}~1~(a) Fig. 1 (a) 传达的信息吗?“ F I D \rm FID FID 反弹意味着
D过拟合了”;对比 F i g . 1 ( b ) ( c ) {\rm Fig.}~1~(b)(c) Fig. 1 (b)(c),我们竟然发现对应 F I D \rm FID FID 反弹的时间,与鉴别器对生成样本的评分分布 D g e n e r a t e d D_{generated} Dgenerated 和对真实样本的评分分布 D t r a i n D_{train} Dtrain “分道扬镳”的时间,是大致吻合的。- 我们又发现:过拟合发生的话,作为验证集的真实样本的得分也 D v a l i d a t i o n D_{validation} Dvalidation 越来越低(虽然始终高于生成样本的分布);这是必然的,因为:
D过拟合➡️D记住了训练用的真实样本➡️D认为除了记住的真实样本外,其他样本(生成样本、验证集的真实样本)都是伪样本,应予以低分。- 再往前看一些,当 绿色线开始脱离蓝色线、随着橙色线下降的时候,
D可能就开始过拟合了。用原文的话就是:when overfitting kicks in, the validation set starts behaving increasingly like the generated images.Q 3 \rm Q3 Q3: 什么时候调整 p p p?
A 3 \rm A3 A3:这时候我们需要定义一些指标,好指定对应的阈值来决定什么时候调整 p p p。
一个最直接的思路是,使用下面的相关关系:
r v = E [ D t r a i n ] − E [ D v a l i d a t i o n ] E [ D t r a i n ] − E [ D g e n e r a t e d ] r_v={{\mathbb E[D_{train}]-\mathbb E[D_{validation}]}\over{\mathbb E[D_{train}]-\mathbb E[D_{generated}]}} rv=E[Dtrain]−E[Dgenerated]E[Dtrain]−E[Dvalidation]理论上,D不发生过拟合的话➡️ D t r a i n ∼ D v a l i d a t i o n D_{train}\sim D_{validation} Dtrain∼Dvalidation➡️D将训练数据和验证数据等同对待➡️ r v = 0 r_v=0 rv=0;D完全过拟合的话➡️ D v a l i d a t i o n ∼ D g e n e r a t e d D_{validation}\sim D_{generated} Dvalidation∼Dgenerated➡️ r v = 1.0 r_v=1.0 rv=1.0。介于两者之间, r v r_v rv 越大,D过拟合越严重,也就越需要通过增大 p p p 来引入更多样化的数据。
**这里的期望 E [ D ? ] \mathbb E[D_?] E[D?] 是通过采样连续的 N N N 个小批量的数据来计算的。(本文使用 N = 4 N=4 N=4)
但作者很快否定了这个方案,因为它需要额外的验证集,这对于很多情况,训练集都不足,验证集就更不用说了。
作者随后提出下面的指标:
r t = E [ s i g n ( D t r a i n ) ] r_t=\mathbb E[{\bf sign}(D_{train})] rt=E[sign(Dtrain)]理论上,D随机初始化使得 D ( x ) D(x) D(x) 的输出分布的期望是 0.0 0.0 0.0;越往后学习,D对真实样本的打分高于生成样本;由于对抗或博弈存在,正常情况下D对两种样本的输出分布都应该跨过 0 0 0 值(估计这里用的是WGAN)。
因此,一开始 E [ s i g n ( D t r a i n ] \mathbb E[{\bf sign}(D_{train}] E[sign(Dtrain] 接近于 0.0 0.0 0.0,但随后会变成 > 0.0 >0.0 >0.0;正常的良性博弈中,这个值应该保持 > 0.0 >0.0 >0.0 且 < 1.0 <1.0 <1.0。
F i g . 1 ( b ) ( c ) {\rm Fig.}~1(b)(c) Fig. 1(b)(c) 展示了,当最后D完全过拟合时, E [ s i g n ( D t r a i n ] = 1.0 \mathbb E[{\bf sign}(D_{train}]=1.0 E[sign(Dtrain]=1.0。
因此,介于 0.0 ∼ 1.0 0.0\sim 1.0 0.0∼1.0 之间, r t r_t rt 越大,D越可能过拟合,也就越需要通过增大 pp 来引入更多样化的数据。Q 4 \rm Q4 Q4: 按什么样的策略调整 p p p?
A 4 \rm A4 A4:本文提出 A D A \rm ADA ADA,其工作机制表述如下:
1️⃣ 初始化 p = 0.0 p=0.0 p=0.0
2️⃣ 每 N = 4 N=4 N=4 个小批量的迭代后,利用顺带统计的 r v r_v rv 或者 r t r_t rt 判断是否需要对 p p p 进行调整;
- 调整的方式是对 p p p 增加或减少一个固定的数值
- 这个数值(步长/Adjustment Size)的选取能够让 p p p 尽可能快地从 0.0 0.0 0.0 上升到 1.0 1.0 1.0,譬如经过 500 k \rm 500k 500k 张图像后
3️⃣ 对更新后的 p p p 作 C l i p \rm Clip Clip 操作。
下面我们看到实验 4 ——
| 实验4( F i g . 5 \rm Fig.~5 Fig. 5) | 说明 |
|---|---|
 | 1️⃣ 实线分别展示了上述两个指标
r
v
r_v
rv 和
r
t
r_t
rt 取不同的阈值,在不同数据集大小下训练 GAN 的结果;2️⃣ 水平虚线是对应数据集大小,使用网格搜索得到的、如果是取固定 p p p 值的话 p p p 的最优值; 3️⃣ 我们可以发现,当这两个指标取值在某个范围内时,动态调整 p p p 的策略对于防止过拟合都是有效的; 4️⃣ 我们选择比较具有应用型更强的 v t v_t vt,其中,取黑色虚竖线的 0.6 作为剩下的实验的 v t v_t vt 的阈值。 |
 | 1️⃣ 图
(
c
)
(c)
(c) 展示的是,在使用
v
t
v_t
vt 动态调整
p
p
p 时候,
p
p
p 在整个训练过程中的变化情况; 2️⃣ 当只有 2 k 2\rm k 2k 的数据时, A u g \rm Aug Aug 在训练的最后几乎总被使用到( p → 1.0 p\rightarrow1.0 p→1.0); p p p 明显超过安全限制 0.8,但作者解释这是因为此时数量太少,以至于 A u g \rm Aug Aug 再怎么频繁使用也还是不够强. |
 | 1️⃣ 图
(
d
)
(d)
(d) 将
r
t
r_t
rt 作为一个 D 性能的指标(纵轴),考虑不同数据集大小下,使用固定的最优
p
p
p (虚线)和使用基于
r
t
r_t
rt 动态调整的
p
p
p (实线),训练过程中,
r
t
r_t
rt 的变化情况;可以看出: 2️⃣ 动态调整下 D 更稳定;3️⃣ 固定的 p p p 值,一开始太强了, D 对于真实的干净样本的置信度不高,但是在训练后阶段,
p
p
p 又显得力不从心,因为明显 D 已经过拟合了,对真实干净样本的置信度普遍很高(正值)。 |
紧接着我们看到实验5——实验5实际上是对实验1的重复,只不过现在增加使用了 A D A \rm ADA ADA 的
D增强策略。
| 实验5( F i g . 6 \rm Fig.~6 Fig. 6) |
|---|
 |
1️⃣ 现在不管数据集大小有多少,训练都可以收敛,不再出现 D 过拟合;2️⃣ 图 ( c ) (c) (c) 说明,没有增强的话, G 接收到的从鉴别器传达的梯度随着训练时间进行会变得越来越简单,D 开始关注少数的特征,G 从而可以无任何代价地生成无意义的或者荒谬的图像;使用
A
D
A
\rm ADA
ADA,D 的梯度始终保持细腻、有意义;3️⃣ 这恰恰好比在回归任务中(如分类、检测、分割),已经被证实使用类似的数据增强手段可以极大提高损失函数的鲁棒性。 |
4. Evaluation
最后我们简单过一下实验部分。
4.1 Training from Scratch
| 实验6( F i g . 7 \rm Fig.~7 Fig. 7) | 说明 |
|---|---|
 | 1️⃣ 这里比较不同 D 增强策略在两个数据集上,不同的数据集大小下训练的 G 的性能;2️⃣ 可以看出,当数据缺乏不严重的时候, b C R \rm bCR bCR 的作用是强于 A D A \rm ADA ADA 的,可以看到大于 50 k 50\rm k 50k 后红色线在绿色线甚至是橙色线下方; 3️⃣ 说明 A D A \rm ADA ADA 在数据足够时可能阻碍 G 学习,这与上文发现的规律是一致的。 |
 | 1️⃣
(
c
)
(c)
(c) 结合
(
a
)
(
b
)
(a)(b)
(a)(b) 说明,在一定范围内,
A
D
A
\rm ADA
ADA 与
b
C
R
\rm bCR
bCR shi协同的; 2️⃣ 但是, b C R \rm bCR bCR 会出现“渗透”,图 ( d ) (d) (d) 的🌰中,使用随机的 x y xy xy-平移 作为 A u g \rm Aug Aug,发现这种平移渗透到生成图像上—— 原本用于训练的、五官对齐的人脸,在取均值后五官变模糊了。 |
紧接着实验7,比较我们的方法与其他对
GAN的优化、改进,也分析了通过降低D的性能来防止过拟合的可行性。这个实验的两个结论才是爆炸性💮的!
| 实验7( F i g 8 \rm Fig~8 Fig 8) | 说明 |
|---|---|
 | 基本上, A D A \rm ADA ADA 对于数据量不充分的情况具有绝对突出的效果! |
 | 1️⃣ 这里对 D 的性能调整,是通过缩放 D 每一层的通道数来实现的;2️⃣ 一个结论是,不管使不使用 A D A \rm ADA ADA,减少 D 性能都是有害的,尽管可以阻止过拟合;3️⃣ 使用 A D A \rm ADA ADA 可以提高模型性能,不管 D d额性能强弱,说明了
A
D
A
\rm ADA
ADA 的一般性! |
4.2 Transfer Learning
顺便说一句, F r e e z e − D \rm Freeze-D Freeze−D 提出,在微调
GAN的时候冻结D的浅层是有效。
| 实验8( F i g . 9 \rm Fig.~9 Fig. 9) |
|---|
 |
1️⃣ 图
(
a
)
(a)
(a) 说明,单纯使用
F
r
e
e
z
e
−
D
\rm Freeze-D
Freeze−D 尽管有效,但是在数据量不足的情况下,无法阻止 D 发生过拟合;2️⃣ 图 ( b ) (b) (b) 说明使用 A D A \rm ADA ADA 可以防止过拟合,与 F r e e z e − D \rm Freeze-D Freeze−D 结合可以进一步提高模型的性能一丶丶; 3️⃣ 图 ( c ) (c) (c) 展示了不同数据集大小下,基线与使用 A D A \rm ADA ADA 与其他微调技巧的结合; 4️⃣ 最有趣的是,图 ( d ) (d) (d) 揭示了微调的一个重要法则:微调 GAN 的最终效果取决于原数据集的多样性,一般从高多样性的数据集微调适应低多样性的数据集,这样的 GAN 微调是更成功的;5️⃣ 图 ( d ) (d) (d) 说明,支持微调的目标数据集的多样性应不高于原数据集的多样性。 |
4.3 Small Datasets
最后作者提出在数据量更少的小样本数据集上训练,并提出使用无偏指标 K I D \rm KID KID 要优于 F I D \rm FID FID。实验 9 结果如下——
| 实验9( F i g . 11 \rm Fig.~11 Fig. 11) |
|---|
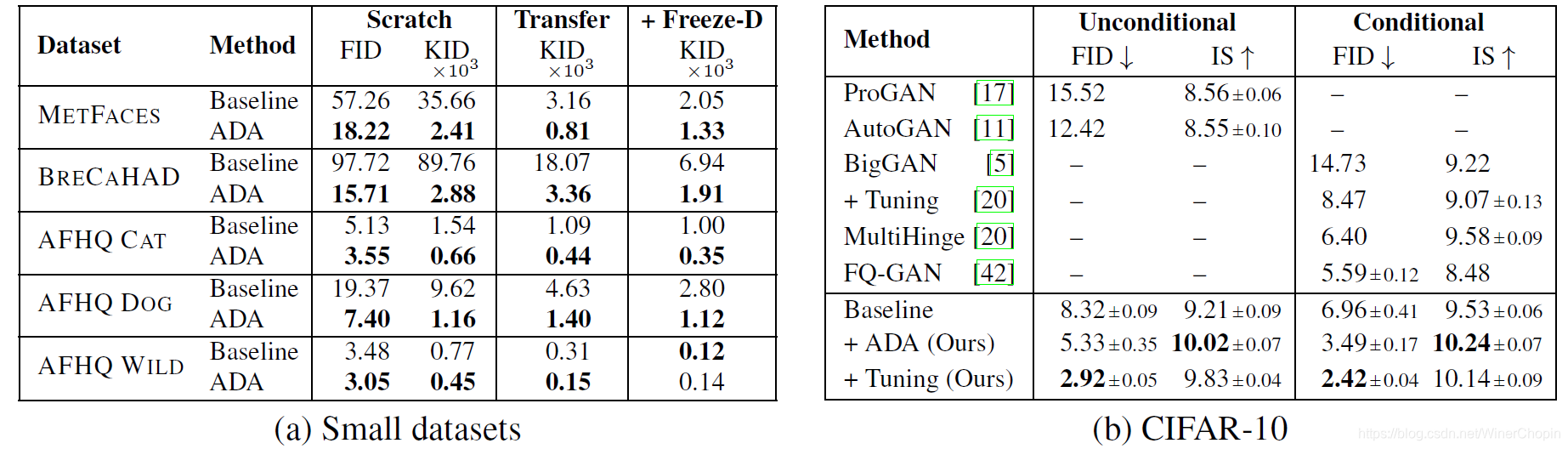 |
表格
(
b
)
(b)
(b) 中的
T
u
n
i
n
g
\rm Tuning
Tuning 是针对 CIFAR-10 数据集的一些微调的 tricks。 |
观摩一下可视化结果,即便是小样本数据集,即便是生成 256 × 256 256\times256 256×256 的高清图像,也不在话下👏👏👏

N V I D I A \rm NVIDIA NVIDIA 关于 G A N \rm GAN GAN 的文章每一次都令人惊叹!









 本文探讨了在小样本数据下训练GAN时,鉴别器D过拟合和生成器G欠拟合的问题。提出了一种名为Stochastic Discriminator Augmentation(SDA)的策略,通过非渗透性数据增强来防止D过拟合,同时确保G不被增强变换影响。实验表明,当增强概率低于0.8时,可以有效避免渗透。此外,提出了自适应鉴别器增强(ADA)方法,根据D的表现动态调整增强强度,以维持D的性能。通过一系列实验,验证了这些策略在不同数据集大小下的有效性,特别是在小样本数据集上,显著提高了GAN的训练效果。
本文探讨了在小样本数据下训练GAN时,鉴别器D过拟合和生成器G欠拟合的问题。提出了一种名为Stochastic Discriminator Augmentation(SDA)的策略,通过非渗透性数据增强来防止D过拟合,同时确保G不被增强变换影响。实验表明,当增强概率低于0.8时,可以有效避免渗透。此外,提出了自适应鉴别器增强(ADA)方法,根据D的表现动态调整增强强度,以维持D的性能。通过一系列实验,验证了这些策略在不同数据集大小下的有效性,特别是在小样本数据集上,显著提高了GAN的训练效果。
















 1280
1280

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








