离散数学概念整理2

命题变元

如果𝑃代表真值未指定的任意命题，我们就称𝑃为命题变元

命题常元

如果𝑃代表一个真值已指定的命题，我们就称𝑃为命题常元。

以“真”、“假”为其变域的变元，称为命题变元；T和F称为命题常元。

命题公式

惯上把含有命题变元的断言称为命题公式。

• 单个命题变元和命题常元叫原子公式。
• 由以下形成规则生成的公式叫命题公式(简称公式):
  ① 单个原子公式是命题公式。
  ② 如果𝐴和𝐵是命题公式，则¬𝐴 、𝐴∧𝐵、𝐴∨𝐵、𝐴→𝐵、𝐴↔𝐵都是命题公式。
  ③ 只有有限步地应用规则①和②生成的公式，才是命题公式。

在不致产生混乱时，我们把命题公式也叫做命题

逻辑等价命题

两个命题公式如果有相同的真值，则称它们是逻辑等价命题

Eg1

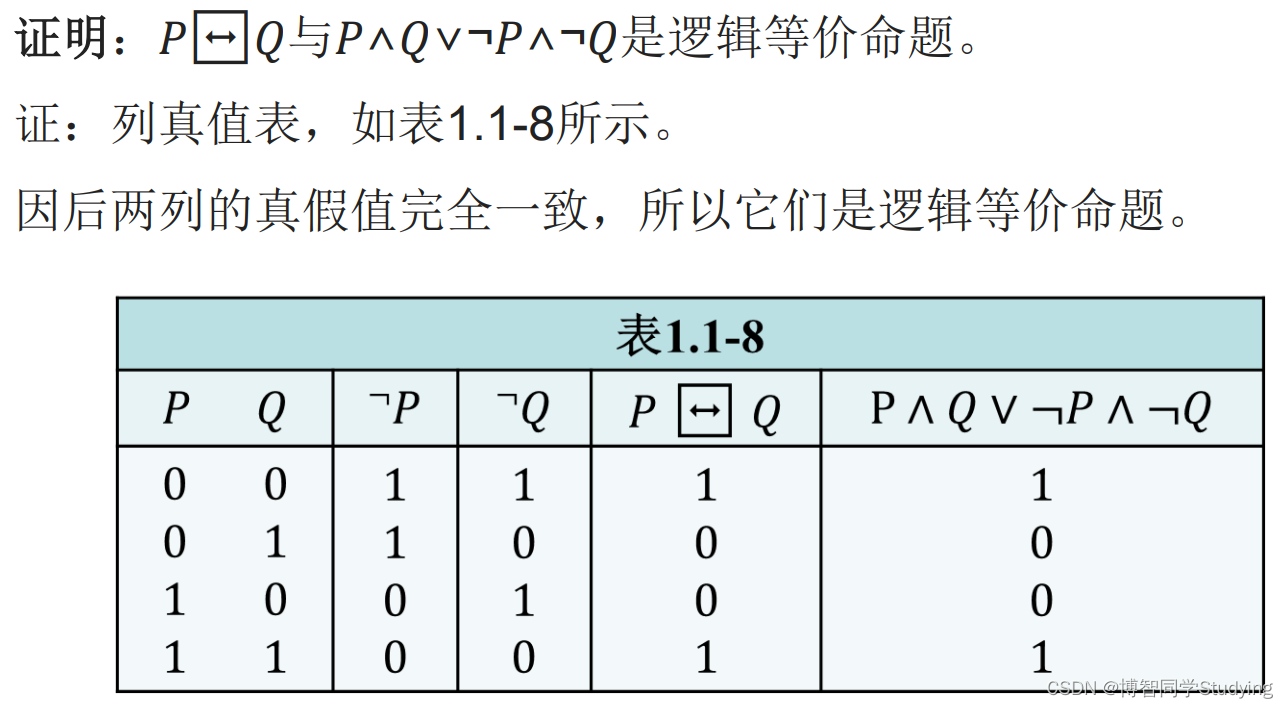
对有𝑛个命题变元的命题公式𝐴(𝑃1, 𝑃2, ⋯ , 𝑃𝑛) ，命题变元的真值有2^𝑛种不同的组合。每一种组合叫做一种指派，一共有2^𝑛种指派，这就是说真值表有2^𝑛行。对应于每一指派，命题式得到一确定的值，即命题公式成为具有真假值的命题，于是可能出现以下情况:

• 重言式（永真式）：对应于所有指派，命题公式均取值真。这种命题公式叫重言式，或叫永真式，例如𝑃∨¬𝑃。

• 矛盾式（永假式）：对应于所有指派，命题公式均取值假。这种命题公式叫矛盾式，或叫永假式，例如𝑃∧¬𝑃 。

• 偶然式：不是永真式，也不是永假式，这种命题公式叫偶然式。

• 矛盾式（永假式）：对应于所有指派，命题公式均取值假。这
  种命题公式叫矛盾式，或叫永假式，例如𝑃∧¬𝑃 。

一个公式如果至少存在一个指派，使其值为真，则称此公式为
可满足的; 一个公式如果至少存在一个指派，使其值为假，则
称此公式为非永真。

• 重言式的否定是矛盾式，矛盾式的否定是重言式，所以研究其
  一就可以了。
• 重言式的合取、析取、蕴含、等值等都是重言式。 这样，由
  简单的重言式可推出复杂的重言式。

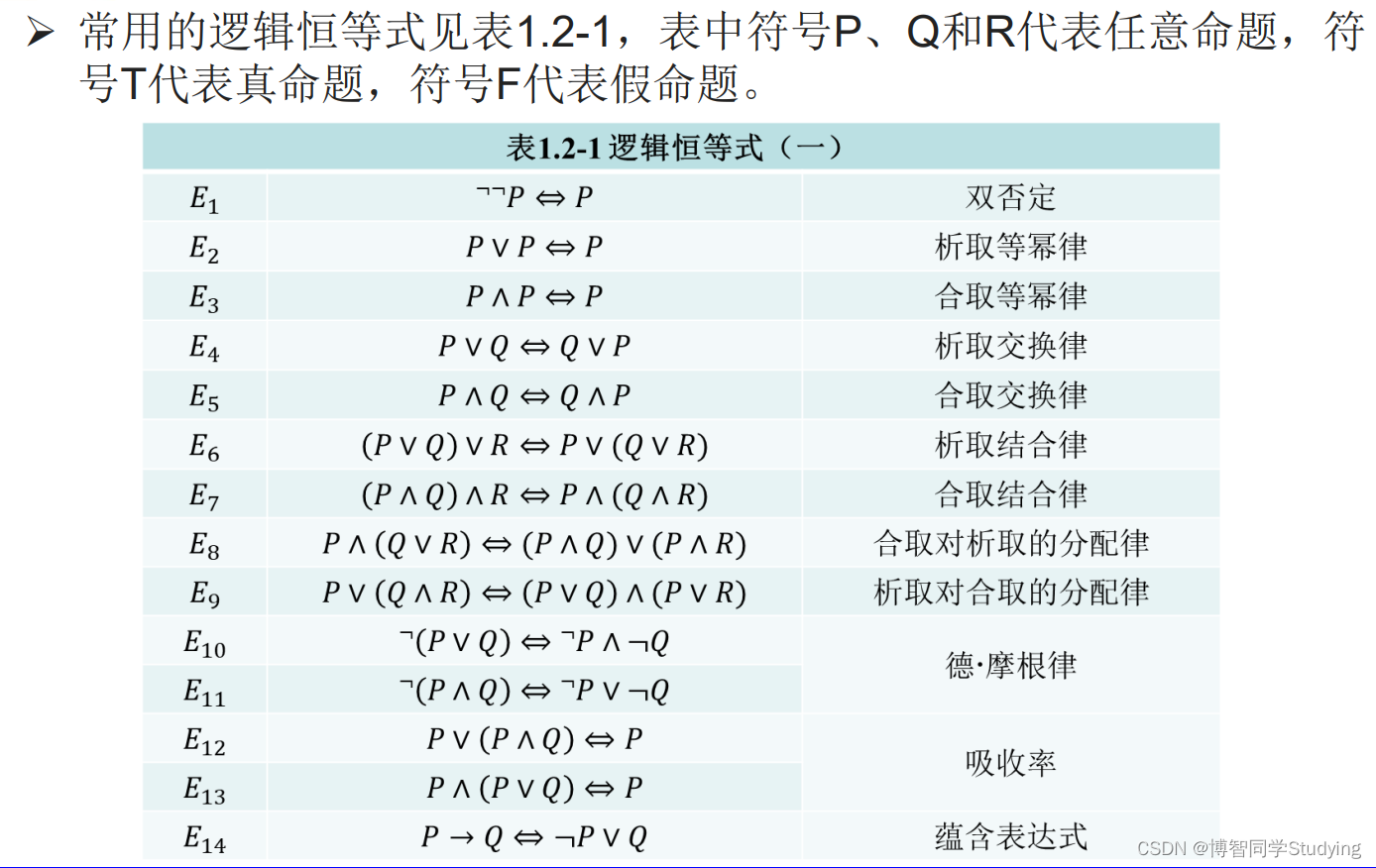
➢ 逻辑恒等式(挺像逻辑等价命题哈)

设𝐴: 𝐴(𝑃1, 𝑃2, ⋯ , 𝑃𝑛)，𝐵: 𝐵(𝑃1, 𝑃2, ⋯ , 𝑃𝑛)是两个命题公式，这里𝑃𝑖 (𝑖 = 1,2, ⋯ , 𝑛)不一定在两公式中同时出现。如果𝐴↔𝐵是重言式，即𝐴与𝐵对任何指派都有相同的真值，此时，记作𝐴⇔𝐵，称为逻辑恒等式，读做“𝐴恒等于𝐵”。

𝐴⇔B 即 A和B逻辑等价的另一种描述方式

➢ 永真蕴涵式

如果𝐴→𝐵是一永真式，那么称为永真蕴含式，记为𝐴⇒𝐵，读做“𝐴永真蕴含𝐵”。

Eg

➢ 证明永真蕴含式𝐼6: (𝑃 → 𝑄) ∧ (𝑄 → 𝑅) ⇒ (𝑃 → 𝑅)。
证明：
✓ 只需证当(𝑃→𝑄)∧(𝑄→𝑅)的真值为真时，(𝑃→𝑅)的真值为真。注意到(𝑃→𝑄)∧(𝑄→𝑅)为真当且仅当𝑃→𝑄和𝑄→𝑅同时为真。假设𝑃→𝑄和𝑄→𝑅同时为真。
显而易见，当𝑃的真值为真且𝑄和𝑅的真值都为真时，假设成立，此时𝑃→𝑅为真；
当𝑃的真值为假且𝑄的真值为假时，假设成立，此时𝑃→𝑅为真；当𝑃的真值为假、𝑄的真值为真且𝑅的真值为真时，假设成立，此时𝑃→𝑅为真。
证毕。

或列真值表

综上

永真蕴含式可用真值表证明，也可用以下办法证明:
(1) 假定前件是真，若能推出后件是真，则此蕴含式是永真蕴含式；
(2) 假定后件是假，若能推出前件是假，则此蕴含式是永真蕴含式(因按逆反律: 𝑃→𝑄⇔¬𝑄→¬𝑃)。

恒等式和永真蕴含式的两个性质

✓ 若𝐴⇔𝐵 、𝐵⇔𝐶 ，则𝐴⇔𝐶;
✓ 若𝐴⇒𝐵、𝐵⇒𝐶，则𝐴⇒𝐶。

代入规则和替换规则

代入规则

一重言式中某个命题变元出现的每一处均代入以同一公式后，所得的仍是重言式。

这条规则之所以正确是由于重言式之值不依赖于变元的值的缘故。例如，𝑃∧¬𝑃⇔F

代入后所得公式称为原公式的代入实例。

替换规则

➢ 设有恒等式𝐴⇔𝐵，若在公式𝐶中出现𝐴的地方替换以𝐵(不必每一处)而得到公式𝐷 ，则𝐶⇔𝐷。
✓ 子公式：如果𝐴是合式公式𝐶中完整的一部分，且𝐴本身是合式公式，则称𝐴是𝐶的子公式。
✓ 规则中“公式𝐶中出现𝐴”意指“𝐴是𝐶的子公式”。
✓ 这条规则的正确性是由于在公式𝐶和𝐷中，除替换部分外均相同，但对任一指派，𝐴和𝐵的真值相同，所以𝐶和𝐷的真值也相同，故 C<=>D

应用这两条规则和已有的重言式可以得出新的重言式。

此处建议多看看课本例题

熟练运用课本上的那个表格

对偶公式

设有公式𝐴，其中仅有联结词∧、∨、¬。在𝐴中将∧ 、∨、𝑇、𝐹分别换以∨、∧、𝐹、𝑇得公式𝐴^∗，则𝐴^∗称为𝐴的对偶公式。对𝐴^∗采取同样手续，又得A，所A也是𝐴^∗的对偶。因此，对偶是相互的。

定理1

设𝐴和𝐴^∗是对偶式，𝑃1, 𝑃2, ⋯ , 𝑃𝑛是出现于𝐴和𝐴^∗中的所有命题变元，于是¬𝐴(𝑃1, 𝑃2, ⋯ , 𝑃𝑛) ⇔ 𝐴^∗(¬𝑃1,¬𝑃2, ⋯ ,¬𝑃𝑛)

定理2

若𝐴⇔𝐵，且𝐴、𝐵为由命题变元𝑃1, 𝑃2, ⋯ , 𝑃𝑛及联结词∧、∨、¬构成的公式，则𝐴^∗ ⇔ 𝐵^∗。
(易由定理1证明)
本定理常称为对偶原理