范数和距离

1、范数

向量的范数可以简单形象的理解为向量的长度，或者向量到零点的距离，或者相应的两个点之间的距离。

向量的范数定义：向量的范数是一个函数||x||,满足非负性||x|| >= 0，齐次性||cx|| = |c| ||x|| ，三角不等式||x+y|| <= ||x|| + ||y||。

向量的范数定义：向量的范数是一个函数||x||,满足非负性||x|| >= 0，齐次性||cx|| = |c| ||x|| ，三角不等式||x+y|| <= ||x|| + ||y||。

常用的向量的范数：
L1范数: ||x|| 为x向量各个元素绝对值之和。
L2范数: ||x||为x向量各个元素平方和的1/2次方，L2范数又称Euclidean范数或者Frobenius范数
Lp范数: ||x||为x向量各个元素绝对值p次方和的1/p次方
L∞范数: ||x||为x向量各个元素绝对值最大那个元素的绝对值，如下：

椭球向量范数: ||x||A = sqrt[T(x)Ax]， T(x)代表x的转置。定义矩阵C 为M个模式向量的协方差矩阵， 设C’是其逆矩阵，则Mahalanobis距离定义为||x||C’ = sqrt[T(x)C’x], 这是一个关于C’的椭球向量范数。

2、 距离

闵可夫斯基距离(Minkowski Distance)，闵氏距离不是一种距离，而是一组距离的定义。对应Lp范数，p为参数。

闵氏距离的定义：两个n维变量（或者两个n维空间点）x₁(x₁₁,x₁₂,…,x_1n)与 x₂(x₂₁,x₂₂,…,x_2n)间的闵可夫斯基距离定义为：

其中p是一个变参数。
当p=1时，就是曼哈顿距离，
当p=2时，就是欧氏距离，
当p→∞时，就是切比雪夫距离，
根据变参数的不同，闵氏距离可以表示一类的距离。

欧式距离（对应L2范数）：最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中。n维空间中两个点x₁(x₁₁,x₁₂,…,x_1n)与 x₂(x₂₁,x₂₂,…,x_2n)间的欧氏距离：

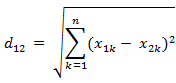
也可以用表示成向量运算的形式：

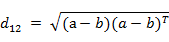
曼哈顿距离：曼哈顿距离对应L1-范数，也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上，坐标（x1, y1）的点P1与坐标（x2, y2）的点P2的曼哈顿距离为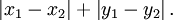：，要注意的是，曼哈顿距离依赖座标系统的转度，而非系统在座标轴上的平移或映射。

切比雪夫距离，若二个向量或二个点x1和x2，其坐标分别为x₁(x₁₁,x₁₂,…,x_1n)与 x₂(x₂₁,x₂₂,…,x_2n)，则二者的切比雪夫距离为：d = max(|x_1i - x_2i|)，i从1到n。对应L∞范数。

Mahalanobis距离：也称作马氏距离。在近邻分类法中，常采用欧式距离和马氏距离。

（1）马氏距离定义
有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到u的马氏距离表示为：

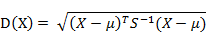
（协方差矩阵中每个元素是各个矢量元素之间的协方差Cov(X,Y)，Cov(X,Y) = E{ [X-E(X)] [Y-E(Y)]}，其中E为数学期望）

而其中向量Xi与Xj之间的马氏距离定义为：

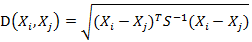
若协方差矩阵是单位矩阵（各个样本向量之间独立同分布）,则公式就成了：

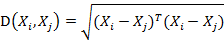
也就是欧氏距离了。　　
若协方差矩阵是对角矩阵，公式变成了标准化欧氏距离。
(2)马氏距离的优缺点：量纲无关，排除变量之间的相关性的干扰。