手把手教你NFA转换成DFA

最新推荐文章于 2025-03-18 16:52:14 发布
最新推荐文章于 2025-03-18 16:52:14 发布
阅读量1w 收藏 63
点赞数 6
分类专栏： 笔记 文章标签： 编译器
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/Z201988009/article/details/120531767
版权
本文详细介绍了非确定有限自动机（NFA）如何转换为确定有限自动机（DFA），通过实例解析了转换过程，包括状态转移的规则和角标的确定。同时，文章探讨了具有ε转移的NFA的转换方法，强调了在转换过程中F状态的处理。内容适合计算机科学与信息技术领域的学生和从业者学习理解。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

首先世界上存在这么一个东西

先写出它的NFA

 

 然后就可以开始转换了

 那么具体是怎么转换的呢？

NFA首先看S

S可以通过0转换成P

所以在对应的DFA里写P

 然后S可以通过1转化成S或R，所以在对应的地方写SR

那么多年后的我可能会问道：他们的角标是怎么来的？

据我观察，每一个中括号里面不同的字母们会对应不同的角标，就像S-A P-B SR-C R-D

这样也可以解释每一行的前面都会有一个字母。

这个字母也是DFA的新状态。

第一行写完之后，第二行就是下一个字符串对应的转化了

所以第二行是P的转化，第三行是SR的转化，这样竖排就对应ABCD

这样依次写下去，没有对应的就直接空格，像SR转换成0P。有重复的只写一个。

这样整个表就写完了。

那么就可以画出DFA

 但是世界上还存在这个东西

那么对于这种NFA，应该怎么转化呢

 

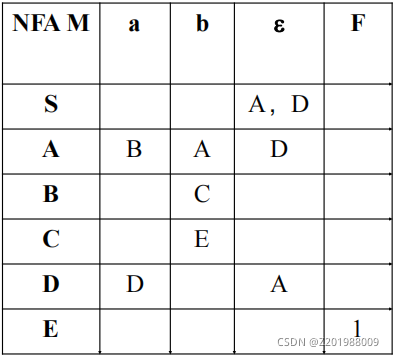
 这个就直接把S加AD，A加D，D加A

 只要转化之后就要加上其对应的状态。

 对于F这一列，只要DFA M这列的中括号里面有E，F就是1

 

从NFA到DFA的转换
Mafia的博客
03-19 1万+
从NFA到DFA的转换例1:简单NFA（不带有空边）例2:从带有空边的NFA到DFA子集构造法词法分析阶段的错误处理查找已扫描字符串中最后一个对应于某终态的字符错误恢复策略 例1:简单NFA（不带有空边） DFA的每个状态都是一个由NFA中的状态构成的集合，即NFA状态集合的一个子集。 转换表： 状态\输入 a b c A {A,B} null null B null {B,C} null C null null {C,D} D null null null 例2:从带有
NFA转换为DFA（子集构造法）
05-17
本人自己花了一整天编的NFA转换为DFA的程序，算法来至编译原理教材（陈意云）
自动机理论实验：NFA转DFA过程实现
最新发布
weixin_42181686的博客
03-18 411
NFA（Non-deterministic Finite Automaton）是一种非确定性有限自动机，它由一组状态、一个起始状态、一组接受状态以及一组转移规则组成。在NFA中，对于一个给定的当前状态和输入符号，可能会有多个可能的下一个状态。这意味着NFA可以同时探索多个状态路径，这是其"非确定性"的含义所在。与DFA相比，NFA可以有更少的状态数量，这使得它们在描述复杂模式时更为高效。
编译原理：NFA转DFA（原理+完整代码+可视化实现）
Toby的博客
12-05 1万+
本文为作者在完成NFA转换为DFA任务过程中的所思所想，欢迎参考与学习！
NFA转化为DFA
gabby____的博客
08-02 5444
NFA转化为DFA        NFA转化为DFA的一种常用方法是子集法。我是参照《编译原理及实践教程》来实现的。这里， 引用该书中内容来加以阐述。                                                                            直接看这些概念应该会很无聊，下面，引用该书中的一个例子，来加以阐述。       ...
NFA转成DFA（子集法）
qq_71547093的博客
10-15 4538
NFA转成DFA（子集法）
NFA到DFA的转化
weixin_48627356的博客
11-14 1万+
文章目录NFA到DFA的转化1.状态集P的 **ɛ** 闭包2.状态集P的a弧线转换集 提示：以下是本篇文章正文内容，下面案例可供参考 NFA到DFA的转化 概念：不确定的有穷自动机(NFA)与确定的有穷自动机(DFA)从功能上来说是等价的，它们所接受的语言类相同。给定一个NFA M’，构造一个DFA M，使得L(M’) = L(M)。以下介绍两个状态子集的计算方法，转化过程需要用到。 1.状态集P的 ɛ 闭包 若P是NFA M’的状态集Q的一个子集，则ɛ - closure§称为状态集P的 ɛ 闭包。计
【构建高效DFA分析器】：手把手教你从零开始
[【构建高效DFA分析器】：手把手教你从零开始](https://www.gastonsanchez.com/r4strings/images/Quantifier_groups.png) # 摘要 本文全面介绍了确定性有限自动机（DFA）分析器的理论与实践应用。首先，概述了DFA...
编译原理项目实战指南：基于燕山大学源码，手把手教你构建编译器
[编译原理项目实战指南：基于燕山大学源码，手把手教你构建编译器](https://www.codeproject.com/KB/architecture/874212/Parser.png) # 摘要 本论文旨在全面探讨编译原理的基础知识、编译器前后端构建的关键技术，...
【编译器构建实验手册】：手把手带你走进编译原理的实验室
词法分析部分介绍了词法单元的分类、有限自动机理论以及构建技术如正则表达式、NFA到DFA的转换和工具Lex/Yacc的应用。语法分析部分涵盖了上下文无关文法、语法分析树、构建技术和错误处理。接着，文章详细讨论了语义...
手把手教学：C语言词法分析器的创建与性能测试
!... # 摘要 本文详细探讨了C语言词法分析器的设计理论、实现实践、性能优化、测试与验证以及扩展应用。首先介绍了词法分析器的基本概念及其在编译过程中的作用。接着，深入讲解了设计词法分析器所涉及的理论基础，包括...
NFA转换成DFA——编译原理
04-25
程序实现了从NFA转化成DFA的功能，输入输出都以状态转换表的形式，读取写入文件。代码比较简单，是编译原理课程的算法实现之一。
编译原理NFA到DFA转换
03-26
关于NFA到DFA的转化过程, 1．分别求ε-closure ε-closure(0) = {0,1,2,4,7} ε-closure(1) = {1,2,4} ε-closure(2) = {2} ε-closure(3) = {1,2,3,4,6,7} ε-closure(4) = {4} ε-closure(5) = {1,2,4,5,6,7} ε-closure(6) = {1,2,4,6,7} ε-closure(7) = {7} ε-closure(8) = {8} ε-closure(9) = {9}
NFA转换成DFA代码
09-05
NFA转换成DFA代码,计算理论Project1
NFA到DFA的转换（C语言实现）
05-14
自己用C语言做的NFA到DFA的转换 有较为详细的备注，希望有所帮助。
NFA转化成DFA
10-18
NFA转化成DFA可视化C++代码，用到OPENCV的东西
NFA到DFA的转换及DFA的简化
热门推荐
小隐的博客
04-17 3万+
还不太了解有穷自动机或是NFA的同学可以先看我的上一篇文章：正则到NFA的转换 确定型有穷自动机
NFA构造及NFA转化为DFA
我飞故我在的专栏
03-25 3万+
在前一篇文章DFA算法的实现与最小化中介绍了DFA,这篇文章将介绍NFA。 1. NFA与DFA的区别 NFA与DFA的主要区别如下: 1) 对于一个特定的符号输入，DFA只会跳转到一个状态；而NFA则可能跳转到多个状态。 2) NFA中一个状态可以不经过任何符号就可以实现状态转换(即存在ε-转移) 上面两个区别就导致了NFA匹配符号串时经常要回溯，而DFA由于状态转移时不存在不确定性，
编译器-NFA转DFA
weixin_43754049的博客
08-07 1369
d1是E-closure of q1 即为集合{q1,q2,q3,q4,q6,q9} 这个集合中没有任何一个state走的通a 所以为d空 走b的话集合中q4可以走到E-closure of q5 是个集合需要设为d2 同理走c的话q6可以走到E-closure of q7 是个集合 需要设为d3。d3是E-closure of q7 走a走不通 设为d空 走b的话q4可以走到E-closure of q5 就是d2 走c的话q6可以走到E-closure of q7 即为自己d3本身。.........
nfa转化为dfa python代码
10-21
NFA（非确定性有限自动机）转化为DFA（确定性有限自动机）是通过子集构造法实现的。以下是使用Python代码实现NFA转化为DFA的过程： ```python class NFA: def __init__(self, states, alphabet, transitions, start_state, final_states): self.states = states self.alphabet = alphabet self.transitions = transitions self.start_state = start_state self.final_states = final_states def epsilon_closure(self, states): closure = set(states) stack = list(states) while stack: current_state = stack.pop() if current_state in self.transitions and 'ε' in self.transitions[current_state]: next_states = self.transitions[current_state]['ε'] new_states = [state for state in next_states if state not in closure] closure.update(new_states) stack.extend(new_states) return closure def move(self, states, symbol): result = set() for state in states: if state in self.transitions and symbol in self.transitions[state]: result.update(self.transitions[state][symbol]) return result def convert_to_dfa(self): dfa_states = [] dfa_transitions = {} start_state = frozenset(self.epsilon_closure([self.start_state])) dfa_states.append(start_state) stack = [start_state] while stack: current_state = stack.pop() for symbol in self.alphabet: next_state = frozenset(self.epsilon_closure(self.move(current_state, symbol))) if next_state not in dfa_states: dfa_states.append(next_state) stack.append(next_state) if current_state not in dfa_transitions: dfa_transitions[current_state] = {} dfa_transitions[current_state][symbol] = next_state dfa_final_states = [state for state in dfa_states if any(final_state in state for final_state in self.final_states)] return DFA(dfa_states, self.alphabet, dfa_transitions, start_state, dfa_final_states) class DFA: def __init__(self, states, alphabet, transitions, start_state, final_states): self.states = states self.alphabet = alphabet self.transitions = transitions self.start_state = start_state self.final_states = final_states def accept(self, input_string): current_state = self.start_state for symbol in input_string: if symbol in self.transitions[current_state]: current_state = self.transitions[current_state][symbol] else: return False return current_state in self.final_states # 示例用法 nfa = NFA( states={'A', 'B', 'C', 'D'}, alphabet={'0', '1'}, transitions={ 'A': {'ε': {'B', 'C'}}, 'B': {'0': {'B'}, '1': {'B', 'D'}}, 'C': {'0': {'C', 'D'}, '1': {'C'}}, }, start_state='A', final_states={'D'} ) dfa = nfa.convert_to_dfa() print(dfa.accept('000')) # 输出 True print(dfa.accept('111')) # 输出 False ``` 上述代码实现了NFA转化为DFA的过程。首先定义了NFA类和DFA类，通过epsilon_closure()方法计算ε-closure，move()方法根据给定的symbol计算下一个状态，然后使用子集构造法将NFA转化为DFA，最后通过DFA类的accept()方法来判断给定的输入字符串是否被DFA接受。
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值