命题范式(propositional normal form)
同一条逻辑表达式,我们可以有很多种写法,将这些表达式写成某一规定形式,称为命题范式。具体包括这样两种范式:合取范式(conjunctive normal form)和析取范式(disjuncive normal form)。
首先,我们利用递归(recursion)的方法定义一个命题式(propositional formula)合法形式:
1.基础步骤:每个命题变元都是一个命题式,真值T、F也是命题式。
2.递归步骤:如果A,B是命题式,那么¬A,A∧B,A∨B,A→B,A↔B也是命题式。
由以上两个步骤,我们就可以根据这种构造规则定义所有的命题式了。
接下来,我们定义单个变元(literal):一个变元或者它的否定称为单个变元:即p和¬p。
最后,我们定义合取子句(conjunctive clause)和析取子句(disjunctive clause)。一个合取子句就是单个变元或其合取,又称为基本加(basicaddition),一个析取子句就是单个变元或其析取,又称基本乘(basic product)。
那么,现在我们就可以看范式了。
析取范式就是多个合取子句的析取,我们可以由以下公式来理解:
(A11∧.....∧A1n)∨.....∨ (Ak1∧.....∧Aknk )
合取范式就是多个析取子句的合取,我们可以由以下公式来理解:
(A11∨.....∨A1n)∧.....∧ (Ak1∨.....∨Aknk )
知道了概念以后,我们可以通过几个特殊的实例来进一步巩固这种认识。
1)单独的p既是析取范式,也是合取范式。因为我们既可以把它看成(p∧T)∨F,也可以看做(p∨F)∧T。
2)类似于p∨q这样的子句,它们既是析取范式,也是合取范式。对于这个例子,我们容易看出它是析取范式,如果把它视为(p∨q)∧T,那么它就是一个合取范式。
)形如¬(p∨q)的式子不是范式。因为它的形式不满足定义,只有转化为¬p∧¬q才能称之为范式。
4)p∧(q∨r)和(p∧q)∨(p∧r)都是范式。
在构造范式的时候,我们首先要去掉→和在括号外的¬(德摩根)。接下来再利用分配律等逻辑等价进行处理。以下是一个去掉上述符号的逻辑表达式的析取范式构造过程:
(p1∧p2) ∨(p3) ∧ (p4∨p5)
(p1∧p2) ∨((p3) ∧ (p4∨p5))
((p1∧p2) ∨(p3)) ∧ ((p1∧p2)∨(p4∨p5))
((p1∨p3)∧ (p2∨p3))∧ ((p1∨p4∨p5)∧(p2∨p4∨p5))
(p1∨p3)∧ (p2∨p3) ∧ (p1∨p4∨p5)∧(p2∨p4∨p5)
接下来我们来看极大项和极小项。
极小项就是单个变元的合取,它包含了所有的变元,并且每个变元只能出现一次。
对于n个变元来说,它有2^n个不同的极小项。比如对于p,q来说,它有四个极小项:p∧q,p∧¬q,¬p∧q,¬p∧¬q。在这2^n个极小项中,只有一个值为真。所以任几个极小项的合取一定为假,所有极小项的析取一定为真,包含为真的极小项的极小项的析取为真。
由于每个变元要么为真要么为假,我们可以用0,1来表示,那么当确定了每个变元的次序后,极小项就可以写成一个位串(bitstring)。对于p,q,r来说,p∧q∧r可以写成111,我们也可以把这个位串化为十进制,得到7。所以我们可以用m7来表示p∧q∧r。
同理,m0=¬p∧¬q∧¬r,m1=¬p∧¬q∧r,m2=¬p∧q∧¬r……以此类推。
对于一个复合命题,由于它的值要么为0要么为1,我们可以把它定义为一个布尔函数f(booleanfunction)。
我们构建一个真值表,已知一个布尔函数f= mj∨mk ∨…∨ml ,我们记f为f=∑m(j,k,..,l)。分别写下变元取不同真值时f的真值。以p、q、r和某一f为例:
p q r f
T T T T
T T F F
T F T T
T F F F
F T T F
F T F F
F F T T
F F F F
其中,m7,m5,m1为真,那么上述f=∑m(1,5,7)。我们通过这种方法构造出了它的主析取范式(Full disjunctive form),即f=(¬p∧¬q∧r)∨( ¬p∧q∧¬r)∨( p∧q∧r)。所谓主析取范式,也就是使f为真的极小项的析取构成的布尔函数。
除了通过真值表,我们也可以通过前文提到的逻辑推理来构造范式。
那么,什么是极大项?极大项就是单个变元的析取,同样地,它包含了所有的变元,并且每个变元只能出现一次。
所以,我们同样可以定义这样一个布尔函数g= mj∧mk ∧…∧ml ,它可以写成g = ∑m({0,1,2,….2n-1}-{j,k,..,l}) =¬f,也就是说它是f的否定。
现在,我们考虑复合命题的可行性。对于一个复合命题来说,当所有变元取某个特定真值(truth assignment)时该复合命题为真,那么这个复合命题就是可行的。前面提到了永真式、可能式、矛盾三种式子,那么我们可以判定可能式和永真式都是可行的。
一个复合命题是不可行的充要条件:它是矛盾,或它的否定是永真式。
例1:2015年浙江大学离散期中考题
Find the full conjunctive normal form of the following compoundproposition .Is there a specific truth value assignment for the variables P,Q,Rand S making the following propositional function FALSE?If so,find the truthvalues of P,Q,R and S.(翻译:找出下面复合命题的主合取范式,是否存在变元P,Q,R,S某一特定真值使得下述命题函数为假?如果存在的话,找出P,Q,R,S的真值)

例2:2015年离散课堂补充习题
Find the full disjunctive form from truth table of following formula
(翻译:通过构造真值表找下述公式的主析取范式)
p q r f
T T T T
T T F T
T F T T
T F F T
F T T F
F T F T
F F T T
F F F T
所以主析取范式为:
如果不用真值表:









 本文介绍了命题逻辑中的命题范式概念,包括合取范式和析取范式,并详细解释了如何构建这些范式,以及如何使用真值表来确定复合命题的主析取范式。
本文介绍了命题逻辑中的命题范式概念,包括合取范式和析取范式,并详细解释了如何构建这些范式,以及如何使用真值表来确定复合命题的主析取范式。
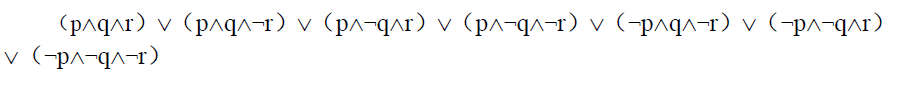
















 5215
5215

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








